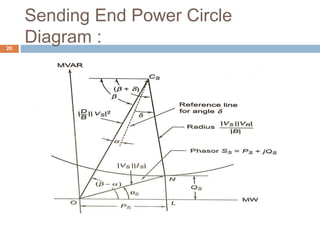
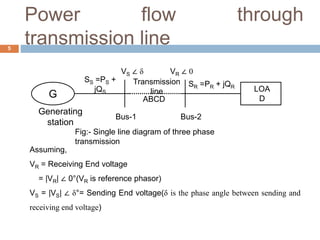
The document outlines power flow through transmission lines, detailing parameters such as inductance, capacitance, resistance, and conductance. It presents analytical and graphical methods for evaluating power flow, including the use of circle diagrams to represent true and reactive power at the receiving end. Key equations and methods for maximizing power transmission are also discussed.

1. Shri Sad Vidya Mandal Institute
Of Technology
Subject :- Electrical Power System-2
Topic :- Power Flow Throuh Transmission Lines
Guided by:-
Pr. N. Kalpana Ray
1

2. Of Semester :-
Ⅵ
2
Presented by Enrol. No.
Hitesh Patel 150450109011
Rajiv Jha 150450109012
Jainil Joshi 150450109013
Pratik Joshi 150450109014
Shri Sad Vidya Mandal Institute
Of Technology
Date:- 21-02-
2018

3. We will be seeing…
 Introduction.
 Power flow through transmission line.
 Single - line diagram of three phase transmission.
 Derivation.
 Circle diagram
 Analytical method.
 Graphical method.
 Summary.
3

4. Introduction
 The electric power generated in the generating station is transmitted using
transmission lines.
 Transmission lines are conductors designed to carry electricity over a long
distances with minimum losses and distortion.
 The parameters associated with these transmission lines are inductance,
capacitance, resistance and conductance.
4

5. Power flow through
transmission line
G
Generating
station
VS ∠ δ VR ∠ 0
SS =PS +
jQS
SR =PR + jQR
LOA
D
Transmission
line
ABCD
Bus-1 Bus-2
Fig:- Single line diagram of three phase
transmission
Assuming,
VR = Receiving End voltage
= |VR| ∠ 0°(VR is reference phasor)
VS = |VS| ∠ δ°= Sending End voltage(δ is the phase angle between sending and
receiving end voltage)
5

6. Power flow through
transmission line
 Generalised line constants are :
A = |A|∠ α ; B = |B| ∠ β; C = |C| ∠ γ; D = |D| ∠ Δ;
 Complex power at receiving end
SR =PR + jQR = VR IR*
 Here,
IR* is conjugate of Receiving end current IR
We know that
VS = AVR + BIR
…eq (1)
6

7. Power flow through
transmission line
 From the above equation
⸫IR =
VS − AVR
B
=
|VS| ∠ δ −|A|∠ α|VR| ∠0°
|B| ∠ β
=
|VS|
|B|
∠ (δ – β ) -
|A||VR|
|B|
∠ (α – β)
i.e. = IR* =
|VS|
|B|
∠ (β − δ ) -
|A||VR|
|B|
∠ (β − α)
…eq (2)
7

8. Power flow through
transmission line
 Now we put the value IR* in equation of …eq (1), we get
SR = VR IR*
=
|Vs||VR|
|B|
∠ (β − δ ) -
|A||VR
2|
|B|
∠(β − α)
 Now, we separate real and imaginary parts, then we get the values of PR and
QR So, Receiving end True power,
PR =
|Vs||VR|
|B|
cos (β − δ ) -
|A||VR
2|
|B|
cos(β − α)
Receiving end Reactive power,
QR =
|Vs||VR|
|B|
sin (β − δ ) -
|A||VR
2|
|B|
sin(β − α)
…eq (4)
…eq (3)
…eq (5)
8

9. Power flow through
transmission line
 For fixed values of Vs and VR, Power Received will be maximum when
cos(β − δ) =1 or when δ= β, So
PR(max) =
|Vs||VR|
|B|
-
|A||VR
2|
|B|
cos(β − α)
and QR(max) = -
|A||VR
2|
|B|
sin(β − α)
 In transmission line
A=D=1∠0°
B=Z ∠ θ
…eq (8)
…eq (7)
9

10. Power flow through
transmission line
 Now we substitute above values in eq (4)&eq (5), We get
⸫PR =
Vs VR
Z
cos(θ − δ) -
VR
2
Z
cos θ
QR =
Vs VR
Z
sin(θ − δ) -
VR
2
Z
sin θ
 Resistance of transmission line is usually very small as compared to
reactance. Hence Z = X and θ = 90 °
⸫ PR =
Vs VR
Z
sin δ
QR =
Vs VR
X
-
VR
2
X
(⸫ δ is the power angle. It is usually very small ⸫ cos
δ=1)
⸫α = 0
β = 0
δ is the power
angle. It is
usually very
small
10

11. Methods Of Finding The
Performance Of Transmission Line.11
 Basically two methods
 Analytical method.
 Graphical method.
 Analytical methods are found to be laborious, while graphical method is
convenient.
 Graphical method or circle diagram are helpful for determination of active
power P, Reactive power Q, power angle δ and power factor for given load
condition.
 Relations between the sending end and receiving end voltage and currents
are given below.
VS = AVR + BIR A, B, C, D are generalised constants of transmission.
IS = CVR + DIR VS = sending end voltage,

12. Methods Of Finding The
Performance Of Transmission Line.12
VR = Receiving end voltage
IS = Sending end current,
IR =Receiving end current.
 By taking either VS, VR, IS or IR as a reference these characteristics can be
plotted.
 These characteristics are nothing but representing circles, hence such
diagrams are called circle diagrams.
 Circle diagram is drawn by taking active power P on X- axis and reactive
power on Y- axis.

13. Receiving End Power Circle
Diagram :13
 Receiving end true power – Horizontal coordinates
 Reactive power component – Vertical coordinates
 From the equation,
 VS = AVR + BIR
 ⸫IR =
VS − AVR
B
=
VS ∠ δ
B ∠ β
-
A ∠ δ
B ∠ β
VR∠ 0
=
Vs
B
∠ (δ − β) -
AVR
B
∠(α− β)

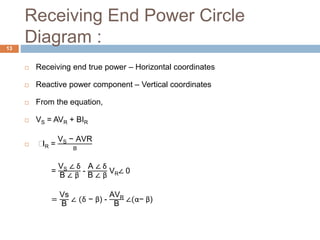
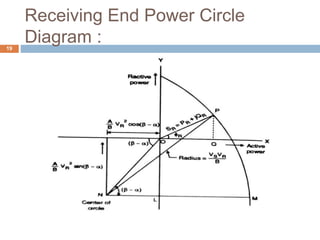
14. Receiving End Power Circle
Diagram :14
 IR* =
|Vs|
|B|
∠ (β − δ ) -
|A||VR|
|B|
∠ (β − α)
 Volt- ampere at the receiving end will be
SR = PR + jQR = VR IR*
=
|Vs||VR|
|B|
∠ (β − δ ) -
|A||VR|2
|B|
∠(β − α)
=
|Vs||VR|
|B|
[cos (β − δ ) + j sin (β − δ )] -
|A||VR|2
|B|
[ cos(β − α)+j sin (β − δ )]
SR =
|Vs||VR|
|B|
cos (β − δ ) -
|A||VR|2
|B|
cos(β − α) +
|Vs||VR|
|B|
j sin (β − δ ) -
|A||VR|2
|B|
j sin (β − δ )

15. Receiving End Power Circle
Diagram :15
 By separating real and imaginary parts, we have
 PR =
|Vs||VR|
|B|
cos (β − δ ) -
|A||VR|2
|B|
cos(β − α)
 QR =
|Vs||VR|
|B|
sin (β − δ ) -
|A||VR|2
|B|
sin(β − α)
 The power component can be expressed as
 PR +
|A||VR|2
|B|
cos(β − α) =
|Vs||VR|
|B|
cos (β − δ )
 QR +
|A||VR|2
|B|
sin(β − α) =
|Vs||VR|
|B|
sin (β − δ )

16. Receiving End Power Circle
Diagram :16
 Squaring and adding these equations will give
{PR +
|A||VR|2
|B|
cos(β − α)}2 + {QR +
|A||VR|2
|B|
sin(β − α) }2
=
|Vs|2|VR|2
|B|
{ cos2(β − δ )+ sin2(β − α)}
=
|Vs|2|VR|2
|B|
 It is an equation of a circle. The coordinates of centre of a circle are:
 X-coordinate of the circle = -
|A||VR|2
|B|
cos(β − α)
 Y- coordinate of the circle = -
|A||VR|2
|B|
sin(β − α)
 Radius of the circle =
|Vs||VR|
|B|

17. Construction of circle diagram:
17
 Plot the centre of the circle N on a suitable scale.
 From N draw an arc of a circle with the calculated radius
VSVR
B
.
 From the origin O draw the load line OP inclined at angle ϕR with the
horizontal.
 Let it cut the circle at P, then the receiving end true power and reactive
power will be represented by OP and PQ respectively.
 If the voltages VS and VR are taken phase voltage in volts then the powers
indicated on X-axis and Y-axis will be in watts and VARs per phase
respectively.

18. Construction of circle diagram:
18
 If the voltages VS and VR are taken line voltage in volts then the powers
indicated on X-axis and Y-axis will be in watts and VARs for all three
phases respectively.
 If the VS and VR are taken from line to line and in kV then the power
indicated will be in MW and MVAR and for all the three phases.
 To determine the maximum power a horizontal line is drawn from the centre
of the circle intersecting vertical axis at the point L and the circle at the
point M.
 Distances LM represents the maximum power for the receiving end.

19. Receiving End Power Circle
Diagram :19

20. Sending End Power Circle
Diagram :20

21. We have seen…
 Receiving end True power,
PR =
|Vs||VR|
|B|
cos (β − δ ) -
|A||VR2|
|B|
cos(β − α)
 Receiving end Reactive power,
QR =
|Vs||VR|
|B|
sin (β − δ ) -
|A||VR
2|
|B|
sin(β − α)
 PR(max) =
|Vs||VR|
|B|
-
|A||VR
2|
|B|
cos(β − α)
 QR(max) = -
|A||VR
2|
|B|
sin(β − α)
 Construction of circle diagram
 Receiving End Power Circle Diagram
 Sending End Power Circle Diagram :
21