The document provides an overview of data structures and algorithms. It defines key terms like data, information, structures, and data structures. It discusses one-dimensional and two-dimensional arrays, including how they are represented in memory in row-major and column-major order. The document also covers topics like algorithms, different types of data structures, operations that can be performed on data, and the difference between static and dynamic data structures.

1. Data Structures &
Algorithms
Dr. Muhammad Idrees

2. Data Structures & Algorithms
(Basic Concepts)
 Data + Structures + Algorithms (all are key
words)
 Data: Data is a raw material/facts & figures from
which we cannot take any kind of decision. E.g. …
Student, Person, City, Country, etc.
 Information: Processed form of data (From which
we made decisions) is called information. E.g. …
Students of BSc CS(Fall 2021)
 Structures: Combination of different things/objects
in an organized form. E.g. Person (id, name,
height, color, listen(), walk(), speak(), etc.)

3.  Data Structure: collection of data
elements in an organized form with some
basic operations/specifications. i.e. array
is a basic data structure
 int list[10];
Data Structures & Algorithms
(Basic Concepts)
0 1 2 3 4 5 6 7 8 9
101 103 105 107 109 111 113 115 117 119
Memory
Address
LB UB

4. One Dimensional Array
 Maximum number of elements in One-Dimensional Array
is computed as under:
Maximum number of elements = UB – LB + 1
UB = Upper Bound LB = Lower Bound
In pervious memory structure UB = 9 and LB = 0
So, Maximum number of elements = 9 – 0 +1 = 10
 Each element of the array also has a unique memory
address
 The starting address of an array is called Base Address.
 Elements of an array occupy a contiguous block of
memory

5. One Dimensional Array
 The memory address of an element with index k is computed
as:
L(X(k)) = L0 + C * (k – 1)
L0 is a Base Address, C memory size of each element in bytes
 Suppose that Base address is 101 and size of element is 2
bytes, what will be the memory address for index 5 (Previous
memory structures)
L0 = 101, C = 2, k = 5
L(X(k))= L0 + C * (k – 1)
L(X(5))= 101 + 2 * (5 – 1)
= 101 + 2 * 4 = 101 + 10 = 111

6. Diagrammatically Representation of
2D-Array
1 2 3 4
1 12 1 -9 23
2 14 7 11 121
3 6 78 15 34
Rows
Columns

7. Two Dimensional Array
 Maximum number of elements in a Two-Dimensional Array
is computed as under:
Maximum number of elements = M x N
M = Number of rows, N = Number of columns
In pervious diagram M = 3 and N = 4
So, Maximum number of elements =3 x 4 = 12
 Each element of an array also has a unique memory
address
 The starting address of an array is called Base Address.
 Elements of an array occupy a contiguous block of memory

8.  Two Dimensional arrays are represented in memory in
two ways.
 Row-major order
Representation of Two-Dimensional
Arrays in memory
12 1 -9 23 14 7 11 121 6 78 15 34
502 504 506 508 510 512 514 516 518 520 522 524
Memory
Address
Values
1st Row 2nd Row 3rd Row
12 14 6 1 7 78 -9 11 15 23 121 34
502 504 506 508 510 512 514 516 518 520 522 524
Memory
Address
Values
1st Col
 Column-major order
Note: Each integer occupies two bytes.
2nd Col 3rd Col 4th Col

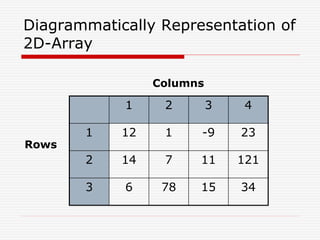
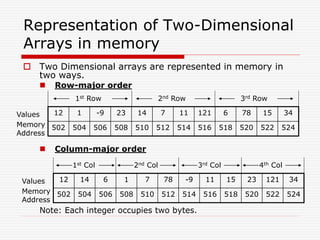
9. Row-Major Order
 The memory address of an element with index i (row) and j
(Col) is computed as:
L(X[i][j]) = L0 + [(i – 1) * N + (j – 1)] * d
L0 is a Base Address, d memory size of each element in
byte
i is a row, j is a col and N is total number of columns of an
array
 Suppose that Base address is 502 and size of each
element is 2 bytes, what will be the memory address for
position x[2][2] (Previous diagram)
L0 = 502, d = 2, i = 2, j = 2, N = 4
L(X[i][j]) = L0 + [(i – 1) * N + (j – 1)] * d
L(X[2][2]) = 502 + [(2 – 1) * 4 + (2 – 1)] * 2
= 502 + [4 + 1] * 2 = 502 + 5 * 2 = 502 + 10 = 512

10. Col-Major Order
 The memory address of an element with index i (row) and j
(Col) is computed as:
L(X[i][j]) = L0 + [(i – 1) + (j – 1) * M] * d
L0 is a Base Address, d memory size of each element in byte
i is a row, j is a col and M is total number of rows of an array
 Suppose that Base address is 502 and size of element is 2
bytes, what will be the memory address for position x[2][2]
(Previous diagram)
L0 = 502, d = 2, i = 2, j = 2, M = 3
L(X[i][j]) = L0 + [(i – 1) + (j – 1) * M] * d
L(X[2][2]) = 502 + [(2 – 1) + (2 – 1) * 3] * 2
= 502 + [1 + 3] * 2 = 502 + 4 * 2 = 502 + 8 = 510

11. Data Structures & Algorithms (Basic
Concepts) Why We Use Arrays?
 For example you want to find smallest numbers amongst
four integer items and suppose that you do not know how
to use array or you do not desire to use it. You may tackle
the problem in the following manner:
 Define four variables to hold four integers data items, i.e.,
int a=10, b=20, c=30; d=5;
 After declaring these variables, you would be required to
write a quite few statements to find the smallest number
in them. Since there are four variables, therefore, you
would need to use four compound if statements for the
solution, such as:

12. Why We Use Arrays?
 if (a<b) && (a<c) && (a<d) cout << “a is the smallest
number in the data”;
 if (b<a) && (b<c) && (b<d) cout << “b is the smallest
number in the data”;
 if (c<a) && (c<b) && (c<d) cout << “c is the smallest
number in the data”;
 if (d<a) && (d<b) && (d<c) cout << “d is the smallest
number in the data”;
 Based on the current data as mentioned above, computer
will produce that “d is the smallest number in the data”.

13. Why we use Array?
Assuming if you would have to find smallest
number amongst 100 data items, off course you
would be required to write 100 compound if
statements and each compound condition made of
99 simple conditions. Further, it would not be
possible to do other application such as sorting
data, finding any particular number in large
amount of data with the use simple data
structures. Therefore, the use of arrays in
programming languages is unavoidable. Processing
on the data such as finding any number,
calculating mean, average and sorting data are
some of the fascinating applications which can be
implemented very easily with the help of array.

14. What are the operations that
can be performed on data?
 Write/Store/Put(): to write any
data specific values at any location of
memory is called store/write.
 Read/Extraction/Retrieve/Get():
to access/get the specific values from
certain location of memory.
 Other Complement Functions are
includes Searching(), Sorting(),
Traversing() etc.

15. Data Structures & Algorithms
(Basic Concepts)
 Algorithms: list of
instructions/statements in a proper
sequence is called as algorithm.
 Write an algorithm for the problem
how to get admission at UET?
 Write an algorithem for insertion
and deletion of specific element for
array data structure?

16. Data Structures & Algorithms
(Basic Concepts)
 Types of data structure:
 Static Data Structure (SDS)
In SDS, no. of data elements are fixed and
memory is allocated to them at compile time
i.e. when you compile the program. Compile
time is also called early/static binding i.e.
array
 Dynamic Data Structure (DDS)
In DDS, no. of data elements are variable
(increased/decreased according to the
requirements) and memory is allocated to them
at run time/execution time. i.e. link list

17. Data Structures & Algorithms
(Basic Concepts)
 Types of static data structures:
 Single data structure
Single data structures are those data structures
whose data elements are not itself data
structures are called single data structures. i.e.
structure
 Composite/compound data structures
In compound data structures, its data elements
are itself data structures. i.e. class,
multidimensional array, etc.

18. Data Structures & Algorithms
(Course Contents)
 Dynamic data structures:
 Link list
 Single link list
 Double link list
 Circular link list
 Stack/LIFO
 Single queue
 De-queue (double ended queue)
 Queue/FIFO
 Tree (hierarchical path)
 Graph

19. Data Structures & Algorithms
(Course Contents)
 Recursion
 Searching techniques
 Linear search
 Binary search
 Sorting techniques
 Linear sort
 Bubble sort
 Sorting by address
 Merge sort
 Radix sort

20. What is difference between
pointer variable and pointer
constant?
 Pointer Vs Variable:
pointer points to any memory location i.e.
int *Px, *Py, *Pz; Px=&x; Py=&y; Pz=&z;
whereas variable points to the
values/contents of that location of variable
i.e. int x, y, z;
 Pointer variable always stores address of
different locations at the same time
whereas pointer constant stores address
of single location.

21. What is the output?
#include<iostream.h>
#include<conio.h>
void main()
{ int *Px, *Py, *Pz;
int x,y,z;
x=y=z=5;
Px=Py=Pz=&x;
*Px=30; *Py=40; Py=&y; Pz=&x;
*Py=*Pz=50; *Px=*Px+*Py+*Pz;
*Py=*Py+*Py;
cout<<*Py<<*Px<<*Pz;
cout<<x<<y<<z;
getch();}

22. Static Data Structure Vs Dynamic
Data Structure (Comparison)
 In SDS, size is fixed and memory is allocated at compile time. In
DDS, size is variable and memory is allocated at run time. In
C++ new operator is used to allocate memory at run time to
pointer to object and delete operator is used to deallocate the
memory. int *Px; Px = new int; int num; Px=&num; delete
Px; int list[size]; const int size =10;
 In SDS, elements are directly accessed but in case of searching
of DDS, it is much slower.
 In SDS, only its data part occupies 2 byte memory but in DDS, it
data part as well as its link part also occupies 2+2 bytes memory.
 In SDS, memory is allocated in consecutive way, but in DDS
memory is allocated in non-consecutive way.
 In SDS, insertion or deletion of any element is too much slow, bu
in DDS insertion or deletion is too much fast.

23. Grading Criteria
 SESSIONAL MARKS: 30%
 ASSIGNMENTS: (Frequently)
 QUIZEZ: (Announced/Surprised)
 PROJECT: (At the end of Final Term)
 PRESENTATIONS/VIVA VOICE:
 Mid Term: 30%
 Final Term: 40%