The document discusses the use of differences-in-differences (DiD) methodology for estimating causal effects, specifically in the context of voter ID laws in Indiana and Georgia. It reviews assumptions, diagnostics, and introduces a new bracketing estimator to address potential confounding effects arising from selective maturation. Key findings highlight the importance of constructing appropriate control groups based on past turnout levels to improve the accuracy of causal estimates in electoral studies.

1. Bracketing Bounds for
Differences-in-Differences with an Application
to Voter ID Laws
Luke Keele
University of Pennsylvania
Joint work with
Raiden Hasegawa & Dylan Small
December 10, 2019

2. DID for Causal Effects
• Differences-in-differences is frequently used for estimating
casual effects.

3. DID for Causal Effects
• Differences-in-differences is frequently used for estimating
casual effects.
• Prototypical DID application: how do changes in state policy
affect outcomes?

4. DID for Causal Effects
• Differences-in-differences is frequently used for estimating
casual effects.
• Prototypical DID application: how do changes in state policy
affect outcomes?
• Motivating application: strict voter ID laws in Indiana and
Georgia.

5. DID for Causal Effects
• Differences-in-differences is frequently used for estimating
casual effects.
• Prototypical DID application: how do changes in state policy
affect outcomes?
• Motivating application: strict voter ID laws in Indiana and
Georgia.
• Let’s do a brief review of DID.

6. Diff-in-Diff: Graphical Interpretation
-
6
r
r
r
r
t = 0 t = 1
E[R00]
E[R10]
E[R01]
E[R11|Z = 1]

7. Diff-in-Diff: Graphical Interpretation
-
6
r
r
r
r
t = 0 t = 1
E[R00]
E[R10]
E[R01]
E[R11|Z = 1]
b

8. Diff-in-Diff: Graphical Interpretation
-
6
r
r
r
r
t = 0 t = 1
E[R00]
E[R10]
E[R01]
E[R11|Z = 1]
bE[R11|Z = 0]

9. Diff-in-Diff: Graphical Interpretation
-
6
r
r
r
r
t = 0 t = 1
E[R00]
E[R10]
E[R01]
E[R11|Z = 1]
bE[R11|Z = 0]
6
?
Treatment Effect

10. Key Assumption and Diagnostics
• Key Assumption: Absent treatment, treated and control
would evolve over time in the same way.

11. Key Assumption and Diagnostics
• Key Assumption: Absent treatment, treated and control
would evolve over time in the same way.
• Standard DID diagnostic: look for parallel trends in
pre-treatment time periods.

12. Key Assumption and Diagnostics
• Key Assumption: Absent treatment, treated and control
would evolve over time in the same way.
• Standard DID diagnostic: look for parallel trends in
pre-treatment time periods.
• But evidence of parallel trends can’t rule the possibility of
selective maturation.

13. Key Assumption
• Selective maturation: an event that occurs concurrently with
the intervention (or shortly thereafter) that differently effects
control and treatment groups.

14. Key Assumption
• Selective maturation: an event that occurs concurrently with
the intervention (or shortly thereafter) that differently effects
control and treatment groups.
• For example, GA adopts voter id, but then becomes a
battleground state in next election.

15. Key Assumption
• Selective maturation: an event that occurs concurrently with
the intervention (or shortly thereafter) that differently effects
control and treatment groups.
• For example, GA adopts voter id, but then becomes a
battleground state in next election.
• In elections, many events can contribute to selective
maturation: e.g. competitive Senate election or a ballot
initiative.

16. Overview
• Review DID bracketing bounds to account for selective
maturation.

17. Overview
• Review DID bracketing bounds to account for selective
maturation.
• Formalize a falsification test for a key assumption.

18. Overview
• Review DID bracketing bounds to account for selective
maturation.
• Formalize a falsification test for a key assumption.
• Develop a new method of sensitivity analysis.

19. Bracketing DID Estimator: Conceptual Sketch
Systematic Variation of Confounder:

20. Bracketing DID Estimator: Conceptual Sketch
Systematic Variation of Confounder:
• Bitterman (1965) introduces the idea of control by
systematic variation to study differences in learning between
species.

21. Bracketing DID Estimator: Conceptual Sketch
Systematic Variation of Confounder:
• Bitterman (1965) introduces the idea of control by
systematic variation to study differences in learning between
species.
• If treated and control groups are comparable on a relevant
confounder U, vary U as much as possible between two
control groups.

22. Bracketing DID Estimator: Conceptual Sketch
Systematic Variation of Confounder:
• Bitterman (1965) introduces the idea of control by
systematic variation to study differences in learning between
species.
• If treated and control groups are comparable on a relevant
confounder U, vary U as much as possible between two
control groups.
• If U cannot entirely explain away effect, evidence from
comparisons between treatment and both control groups
should agree.

23. Bracketing DID Estimator: Conceptual Sketch
• Find a second control group that differs with respect to a
key unobserved confounder.

24. Bracketing DID Estimator: Conceptual Sketch
• Find a second control group that differs with respect to a
key unobserved confounder.
• In a DID study, we can exploit the availability of control units
that had systematically higher and lower levels of the
outcome before treatment.

25. Bracketing DID Estimator: Conceptual Sketch
• States that differ on past turnout levels may differ on U a
possibly key unobservable.

26. Bracketing DID Estimator: Conceptual Sketch
• States that differ on past turnout levels may differ on U a
possibly key unobservable.
• Form separate control groups based on past turnout.

27. Bracketing DID Estimator: Conceptual Sketch
• States that differ on past turnout levels may differ on U a
possibly key unobservable.
• Form separate control groups based on past turnout.
• Upper Control Group: comprised of units with higher
outcomes than the treated group based on the before period.

28. Bracketing DID Estimator: Conceptual Sketch
• States that differ on past turnout levels may differ on U a
possibly key unobservable.
• Form separate control groups based on past turnout.
• Upper Control Group: comprised of units with higher
outcomes than the treated group based on the before period.
• Lower Control Group: comprised of units with lower
outcomes than the treated group based on the before period.

29. Bracketing DiD Estimator: Conceptual Sketch
• Apply DID estimator using lower controls.

30. Bracketing DiD Estimator: Conceptual Sketch
• Apply DID estimator using lower controls.
• Apply DID estimator using upper controls.

31. Bracketing DiD Estimator: Conceptual Sketch
• Apply DID estimator using lower controls.
• Apply DID estimator using upper controls.
• These two estimates bracket the true causal effect under a
set of identification assumptions.

32. Bracketing DiD Estimator: Conceptual Sketch
• Apply DID estimator using lower controls.
• Apply DID estimator using upper controls.
• These two estimates bracket the true causal effect under a
set of identification assumptions.
• These assumptions may be more realistic than standard DID
assumptions.

33. Potential Outcome Model
Let Y
(d)
ip be the potential outcome of

34. Potential Outcome Model
Let Y
(d)
ip be the potential outcome of
• individual i
• in period p (0 = before exposure 1 = after exposure)

35. Potential Outcome Model
Let Y
(d)
ip be the potential outcome of
• individual i
• in period p (0 = before exposure 1 = after exposure)
• with exposure d (0 or 1) where d = 0 if p = 0.

36. Potential Outcome Model
Let Y
(d)
ip be the potential outcome of
• individual i
• in period p (0 = before exposure 1 = after exposure)
• with exposure d (0 or 1) where d = 0 if p = 0.
• G denotes group (t, lc, uc).

37. Potential Outcome Model
Let Y
(d)
ip be the potential outcome of
• individual i
• in period p (0 = before exposure 1 = after exposure)
• with exposure d (0 or 1) where d = 0 if p = 0.
• G denotes group (t, lc, uc).
• Ui is an unmeasured confounder whose distribution is
time-invariant.

38. Potential Outcome Model
Let Y
(d)
ip be the potential outcome of
• individual i
• in period p (0 = before exposure 1 = after exposure)
• with exposure d (0 or 1) where d = 0 if p = 0.
• G denotes group (t, lc, uc).
• Ui is an unmeasured confounder whose distribution is
time-invariant.

39. Potential Outcome Model
Consider the model
Y
(d)
ip = h(Ui , p) + βd + ip

40. Potential Outcome Model
Consider the model
Y
(d)
ip = h(Ui , p) + βd + ip
where
• h is increasing in U: h(U, p) ≥ h(U , p) if U ≥ U
• is independent of period and group.

41. Potential Outcome Model
Consider the model
Y
(d)
ip = h(Ui , p) + βd + ip
where
• h is increasing in U: h(U, p) ≥ h(U , p) if U ≥ U
• is independent of period and group.
Related Models: this model nests the standard
difference-in-difference model and changes-in-changes model of
Athey and Imbens (2006).

42. Bracketing Assumptions
Assmp. (1) The within group distrbutions of U are stochastically
ordered:
U|G = lc U|G = t U|G = uc ,
meaning that
E[f (U)|G = lc] ≤ E[f (U)|G = t] ≤ E[f (U)|G = uc] for any
bounded, increasing function f .

43. Bracketing Assumptions
Assmp. (1) The within group distrbutions of U are stochastically
ordered:
U|G = lc U|G = t U|G = uc ,
meaning that
E[f (U)|G = lc] ≤ E[f (U)|G = t] ≤ E[f (U)|G = uc] for any
bounded, increasing function f .
• In words: Higher values of U correspond to higher outcomes.

44. Bracketing Assumptions
Assmp. (1) The within group distrbutions of U are stochastically
ordered:
U|G = lc U|G = t U|G = uc ,
meaning that
E[f (U)|G = lc] ≤ E[f (U)|G = t] ≤ E[f (U)|G = uc] for any
bounded, increasing function f .
• In words: Higher values of U correspond to higher outcomes.
• U is unobserved mobilization effort.

45. Bracketing Assumptions
Assmp. (1) The within group distrbutions of U are stochastically
ordered:
U|G = lc U|G = t U|G = uc ,
meaning that
E[f (U)|G = lc] ≤ E[f (U)|G = t] ≤ E[f (U)|G = uc] for any
bounded, increasing function f .
• In words: Higher values of U correspond to higher outcomes.
• U is unobserved mobilization effort.
• Higher values of U likely lead to higher levels of turnout.

46. Bracketing Assumptions
Assmp (2) The unspecified function h(U, t) is bounded and
increasing in U for every t.
• Natural when higher levels of unmeasured confounder
corresponds to higher value of the outcome.
• Changes-in-changes model (Athey and Imbens, 2006) also
makes an identical assumption.

47. Bracketing Assumptions
Assmp (3) The effect of time is either (i) greater at higher
values of U over the whole range of U or (ii) smaller over the
whole range of U, U:
(i) h(U, 1) − h(U, 0) ≥ h(U , 1) − h(U , 0) for all U ≥ U , U, U ∈ U .
(ii) h(U, 1) − h(U, 0) ≤ h(U , 1) − h(U , 0) for all U ≥ U , U, U ∈ U .

48. Bracketing Assumptions
Assmp (3) The effect of time is either (i) greater at higher
values of U over the whole range of U or (ii) smaller over the
whole range of U, U:
(i) h(U, 1) − h(U, 0) ≥ h(U , 1) − h(U , 0) for all U ≥ U , U, U ∈ U .
(ii) h(U, 1) − h(U, 0) ≤ h(U , 1) − h(U , 0) for all U ≥ U , U, U ∈ U .
• Another way to say (3): distribution of U must be time
invariant within the treated and control groups.

49. Bracketing Assumptions
Assmp (3) The effect of time is either (i) greater at higher
values of U over the whole range of U or (ii) smaller over the
whole range of U, U:
(i) h(U, 1) − h(U, 0) ≥ h(U , 1) − h(U , 0) for all U ≥ U , U, U ∈ U .
(ii) h(U, 1) − h(U, 0) ≤ h(U , 1) − h(U , 0) for all U ≥ U , U, U ∈ U .
• Another way to say (3): distribution of U must be time
invariant within the treated and control groups.
• U is unobserved mobilization effort.

50. Bracketing Assumptions
Assmp (3) The effect of time is either (i) greater at higher
values of U over the whole range of U or (ii) smaller over the
whole range of U, U:
(i) h(U, 1) − h(U, 0) ≥ h(U , 1) − h(U , 0) for all U ≥ U , U, U ∈ U .
(ii) h(U, 1) − h(U, 0) ≤ h(U , 1) − h(U , 0) for all U ≥ U , U, U ∈ U .
• Another way to say (3): distribution of U must be time
invariant within the treated and control groups.
• U is unobserved mobilization effort.
• Roughly constant with respect to time at state level due to
winner take all nature of electoral college.

51. Bracketed Causal Effects
Consider the expectation of the standard DiD estimator using
lower control group lc:

52. Bracketed Causal Effects
Consider the expectation of the standard DiD estimator using
lower control group lc:
E ˆβdd.lc =
β + (E[h(U, 1) − h(U, 0)|G = t]) − (E[h(U, 1) − h(U, 0)|G = lc])

53. Bracketed Causal Effects
Consider the expectation of the standard DiD estimator using
lower control group lc:
E ˆβdd.lc =
β + (E[h(U, 1) − h(U, 0)|G = t]) − (E[h(U, 1) − h(U, 0)|G = lc])
Similar logic yields,
E ˆβdd.uc =
β +(E[h(U, 1) − h(U, 0)|G = t])−(E[h(U, 1) − h(U, 0)|G = uc])

54. Bracketed Causal Effects
Proposition (Bracketing Estimator)
Under assumptions (1) and (2),
min E ˆβdd.lc , E ˆβdd.uc ≤ β ≤ max E ˆβdd.lc , E ˆβdd.uc .

55. Bracketed Causal Effects
Proposition (Bracketing Estimator)
Under assumptions (1) and (2),
min E ˆβdd.lc , E ˆβdd.uc ≤ β ≤ max E ˆβdd.lc , E ˆβdd.uc .
Corollary
The shortest interval that contains both 1 − α intervals for ˆβdd.lc
and ˆβdd.uc is a valid CI for β.

56. Addressing a Plausible Pattern of Bias:
DID Bracketing estimator removes history-by-group interaction
bias arising from an unobserved confounder that has an increasing
or decreasing effect on voter turnout over time.

57. Building Upper and Lower Control Groups
• How do we construct the upper and lower control groups?

58. Building Upper and Lower Control Groups
• How do we construct the upper and lower control groups?
• Use states with turnout above or below that of IN/GA to
form upper and lower control groups.

59. Building Upper and Lower Control Groups
• How do we construct the upper and lower control groups?
• Use states with turnout above or below that of IN/GA to
form upper and lower control groups.
• To avoid, regression to the mean, we define 2004 as the
before period, and use 1996 and 2000 to form upper and
lower controls.

60. Building Upper and Lower Control Groups
• How do we construct the upper and lower control groups?
• Use states with turnout above or below that of IN/GA to
form upper and lower control groups.
• To avoid, regression to the mean, we define 2004 as the
before period, and use 1996 and 2000 to form upper and
lower controls.
• Using pooled 1996 and 2000 data, we estimated state fixed
effects and select up to 5 states with upper and lower
turnout.

61. Estimation
• We applied linear DID estimators with usual set of voter
turnout controls.

62. Estimation
• We applied linear DID estimators with usual set of voter
turnout controls.
• One can use any DID estimator for this step.

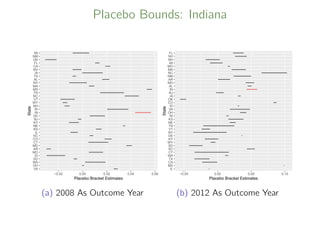
63. DID Bracketing Estimates for Indiana
2008
DID Point Estimate 95% CI
Lower Control Group 4.4 [3.3, 5.4]
Upper Control Group 5.7 [4.2, 7.1]
Bounds [3.3, 7.1]
2012
DID Point Estimate 95% CI
Lower Control Group 5.9 [3.1, 8.6]
Upper Control Group 4.3 [3.3, 5.4]
Bounds [3.1, 8.6]

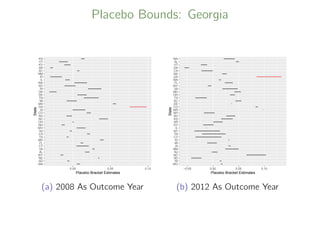
64. DID Bracketing Estimates for Georgia
2008
DID Point Estimate 95% CI
Lower Control Group 9.8 [6.5, 13.1]
Upper Control Group 7.6 [6.3, 8.9]
Bounds [6.3, 13.1]
2012
DID Point Estimate 95% CI
Lower Control Group 13.4 [12.0, 14.8]
Upper Control Group 8.5 [6.7, 10.4]
Bounds [6.7, 14.8]

65. Sources of Uncertainty: A Placebo Study
• Regression estimators with fixed effects may understate
standard errors in the presence of serially correlated data, or
yearly state-level shocks.

66. Sources of Uncertainty: A Placebo Study
• Regression estimators with fixed effects may understate
standard errors in the presence of serially correlated data, or
yearly state-level shocks.
• Should check inference via placebo test.

67. Sources of Uncertainty: A Placebo Study
• For each non-voter ID state, we identified a set of lower and
upper controls.

68. Sources of Uncertainty: A Placebo Study
• For each non-voter ID state, we identified a set of lower and
upper controls.
• We then designated each non-voter ID state as a treated unit
and estimated the DID bounds using these control groups.

69. Sources of Uncertainty: A Placebo Study
• For each non-voter ID state, we identified a set of lower and
upper controls.
• We then designated each non-voter ID state as a treated unit
and estimated the DID bounds using these control groups.
• We then repeated this process for every non-voter ID state.

70. Sources of Uncertainty: A Placebo Study
• For each non-voter ID state, we identified a set of lower and
upper controls.
• We then designated each non-voter ID state as a treated unit
and estimated the DID bounds using these control groups.
• We then repeated this process for every non-voter ID state.
• The result is a distribution of estimates that are zero by
construction that can serve as a null distribution.

71. Placebo Bounds: Indiana
VA
OH
WA
SD
ID
MO
AR
MD
CT
CO
SC
IL
KS
NE
KY
NJ
DE
IN
RI
NH
WY
VT
NC
TN
MS
MA
NY
AL
TX
IA
NV
CA
FL
OK
NM
MI
−0.02 0.00 0.02 0.04 0.06
Placebo Bracket Estimates
State
(a) 2008 As Outcome Year
IL
MS
CA
TX
WA
CT
SC
SD
WY
KY
DE
NY
VT
TN
NE
KS
RI
OH
VA
ID
CO
OK
IA
NJ
IN
AL
MD
AR
NM
NC
MA
MO
MI
NH
NV
FL
−0.05 0.00 0.05 0.10
Placebo Bracket Estimates
State
(b) 2012 As Outcome Year

72. Placebo Bounds: Georgia
MA
SD
NE
WY
AL
VA
CT
FL
MD
TX
CA
NJ
MO
NH
OH
NC
NV
CO
IA
GA
MS
MI
TN
DE
OK
RI
NY
WA
IL
ID
NM
SC
AR
KY
VT
KS
0.00 0.05 0.10
Placebo Bracket Estimates
State
(a) 2008 As Outcome Year
MO
RI
SD
NC
NJ
NM
IA
MI
ID
CT
TN
NY
IL
KY
AR
KS
NV
NH
MS
CO
DE
SC
TX
OH
MD
VA
WY
FL
WA
GA
NE
CA
OK
VT
AL
MA
−0.05 0.00 0.05 0.10
Placebo Bracket Estimates
State
(b) 2012 As Outcome Year

73. A Falsification Test
• Next, we formalize a falsification test for a key assumption.

74. A Falsification Test
• Next, we formalize a falsification test for a key assumption.
• The falsification test uses data from a set of time periods
before t = 1.

75. A Falsification Test
• Next, we formalize a falsification test for a key assumption.
• The falsification test uses data from a set of time periods
before t = 1.
• We denote these time periods with −t ∈ {−2, −1}, where -1
indicates a time period before t = 1 and -2 indicates a time
period prior to t = −1.

76. A Falsification Test
• Next, we formalize a falsification test for a key assumption.
• The falsification test uses data from a set of time periods
before t = 1.
• We denote these time periods with −t ∈ {−2, −1}, where -1
indicates a time period before t = 1 and -2 indicates a time
period prior to t = −1.
• We test four separate patterns that are consistent with the
assumptions.

77. A Falsification Test
The first pattern is
E[Y (−1)
|Zi = 1] − E[Y (−2)
|Zi = 1]
E[Y (−1)
|Zi = 0] − E[Y (−2)
|Zi = 0]
βuc,−t = E[Y (−1)
|Zi = 1] − E[Y (−2)
|Zi = 1] −
E[Y (−1)
|Zi = 0] − E[Y (−2)
|Zi = 0]
Test as: H(iii)[a] : βuc,−t 0 using p(iii)[a]

78. A Falsification Test
The second pattern is
E[Y (−1)
|Di = 1] − E[Y (−2)
|Di = 1]
E[Y (−1)
|Di = 0] − E[Y (−2)
|Di = 0] .
Test as: H(iii)[b] : βlc,−t 0 using p(iii)[b]

79. A Falsification Test
The third pattern is:
E[Y (−1)
|Zi = 1] − E[Y (−2)
|Zi = 1]
E[Y (−1)
|Zi = 0] − E[Y (−2)
|Zi = 0]
Test: H(iv)[a] : βuc,−t 0 using p(iv)[a]

80. A Falsification Test
The fourth pattern is:
E[Y (−1)
|Di = 1] − E[Y (−2)
|Di = 1]
E[Y (−1)
|Di = 0] − E[Y (−2)
|Di = 0]
Test: H(iv)[a] : βul,−t 0 using p(iv)[b]

81. A Falsification Test
Test Hc
(iii) with p(iii) = max{p(iii)[a], p(iii)[b]}
Test Hc
(iv) with p(iv) = max{p(iii)[a], p(iii)[b]}

82. A Falsification Test
Test the overall proposition with the following compound
hypothesis:
Hc
v : Hc
(iii) ∩ Hc
(iv)
which can be tested using the intersection union test which
rejects if p = min min{p(iii), p(iv)} × 2, 1 ≤ α

83. A Falsification Test
• We tested for these patterns in the data.

84. A Falsification Test
• We tested for these patterns in the data.
• Indiana results: piii : 0.06 and piv : 0.94, and p = .12.

85. A Falsification Test
• We tested for these patterns in the data.
• Indiana results: piii : 0.06 and piv : 0.94, and p = .12.
• Georgia results: p(iii) = .44 and p(iv) = .96, and p = .89

86. A Falsification Test
• We tested for these patterns in the data.
• Indiana results: piii : 0.06 and piv : 0.94, and p = .12.
• Georgia results: p(iii) = .44 and p(iv) = .96, and p = .89
• In both cases, we can reject.

87. A Falsification Test
• We tested for these patterns in the data.
• Indiana results: piii : 0.06 and piv : 0.94, and p = .12.
• Georgia results: p(iii) = .44 and p(iv) = .96, and p = .89
• In both cases, we can reject.
• The data do not contradict the identification strategy.

88. A Sensitivity Analysis
• We developed a sensitivity analysis, which adjusted the
estimated bounds based on bias estimated from the placebo
time period.

89. Sensitivity Analysis
• Estimate DID Bracket bounds 95% CI: τCIlo
and τCIup .

90. Sensitivity Analysis
• Estimate DID Bracket bounds 95% CI: τCIlo
and τCIup .
• Adjust these via a Berger and Boos correction to form
97.5% CI: τCIBBlb
and τCIBBub

91. Sensitivity Analysis
• Estimate DID Bracket bounds 95% CI: τCIlo
and τCIup .
• Adjust these via a Berger and Boos correction to form
97.5% CI: τCIBBlb
and τCIBBub
• Estimate 8 correction factors using pre-study time periods:
da, da2, db, db2, −da, −da2, −db, −db2.

92. Sensitivity Analysis
• Estimate DID Bracket bounds 95% CI: τCIlo
and τCIup .
• Adjust these via a Berger and Boos correction to form
97.5% CI: τCIBBlb
and τCIBBub
• Estimate 8 correction factors using pre-study time periods:
da, da2, db, db2, −da, −da2, −db, −db2.
• These represent the worst case possible violations in terms of
how much they increase the length of τCIBBlb
and τCIBBub
.

93. Sensitivity Analysis Bounds
The sensitivity bounds are:
LBsens = min[(τCIBBlb
−db2, τCIBBlb
−da), (τCIBBlb
−db, τCIBBlb
−da2)]
UBsens = max[(τCIBBub
− (−db2), τCIBBub
− (−da)),
(τCIBBub
− (−db), τCIBBub
− (−da2))]

94. Sensitivity Analysis
Table: Sensitivity Analysis for Indiana
2008
DID Bracketing Bounds [3.3, 7.1]
Sensitivity Analysis Bounds [1.7, 12.0]
2012
DID Bracketing Bounds [3.1, 8.6]
Sensitivity Analysis Bounds [0.0, 18.0]

95. Sensitivity Analysis
Table: Sensitivity Analysis for Georgia
2008
DID Bracketing Bounds [6.3, 13.1]
Sensitivity Analysis Bounds [1.2, 13.6]
2012
DID Bracketing Bounds [6.7, 14.8]
Sensitivity Analysis Bounds [-1.2, 15.0]

96. Summary of Results
• Assumptions are relatively easy to interpret.

97. Summary of Results
• Assumptions are relatively easy to interpret.
• More plausible than DID assumptions when selective
maturation is a threat.

98. Summary of Results
• Assumptions are relatively easy to interpret.
• More plausible than DID assumptions when selective
maturation is a threat.
• Easy to implement - you don’t need a new R package.

99. Summary of Results
• Assumptions are relatively easy to interpret.
• More plausible than DID assumptions when selective
maturation is a threat.
• Easy to implement - you don’t need a new R package.
• Allows you to use your favorite DID estimator.

100. Extensions
• We used levels of Yi,t−1(0) to select the upper and lower
controls.

101. Extensions
• We used levels of Yi,t−1(0) to select the upper and lower
controls.
• Instead we could select the controls using Yi,t(0) − Yi,t−1(0)

102. Extensions
• We used levels of Yi,t−1(0) to select the upper and lower
controls.
• Instead we could select the controls using Yi,t(0) − Yi,t−1(0)
• Extend to multiple time periods and treatments that are
adopted over time.