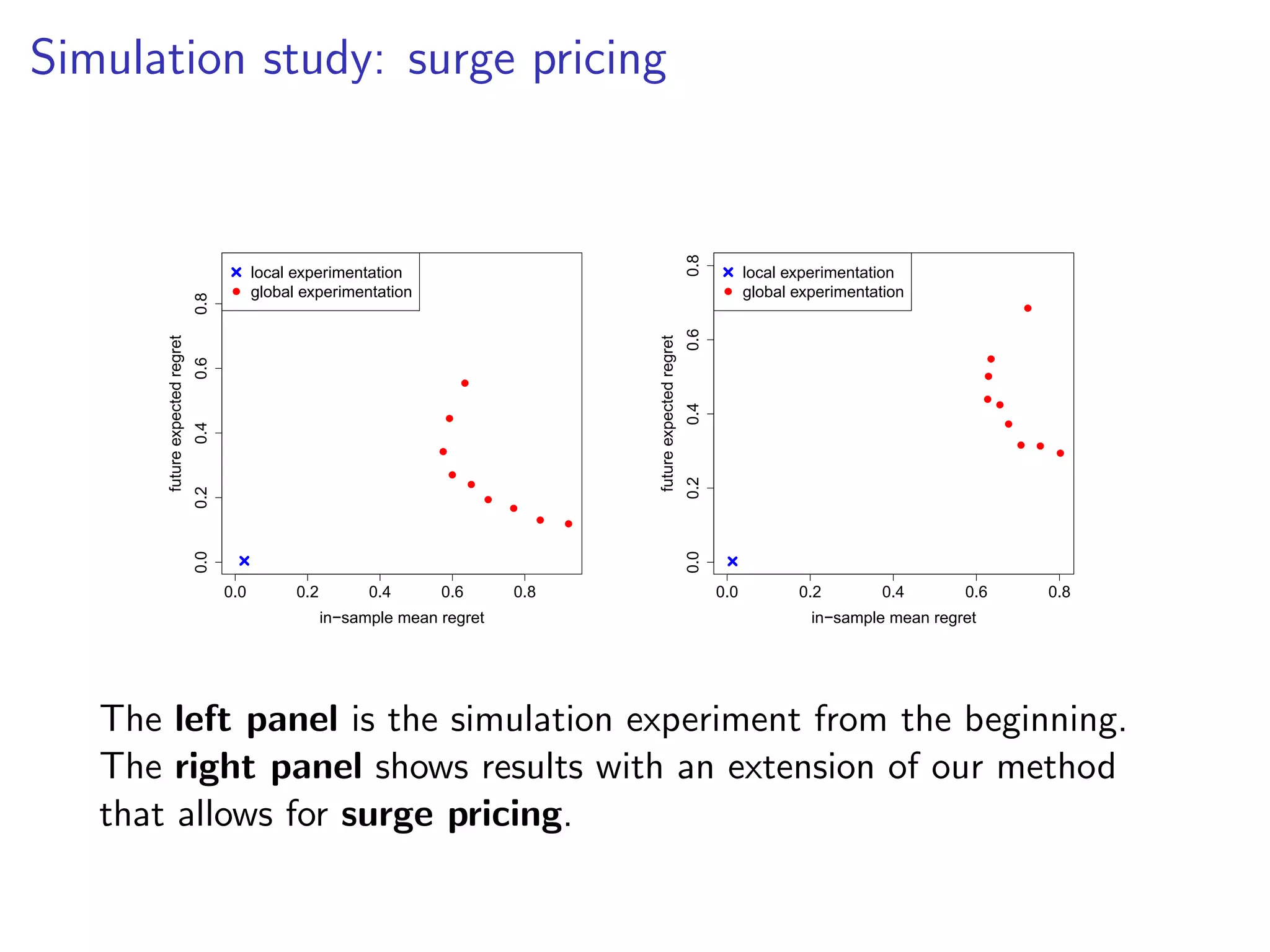
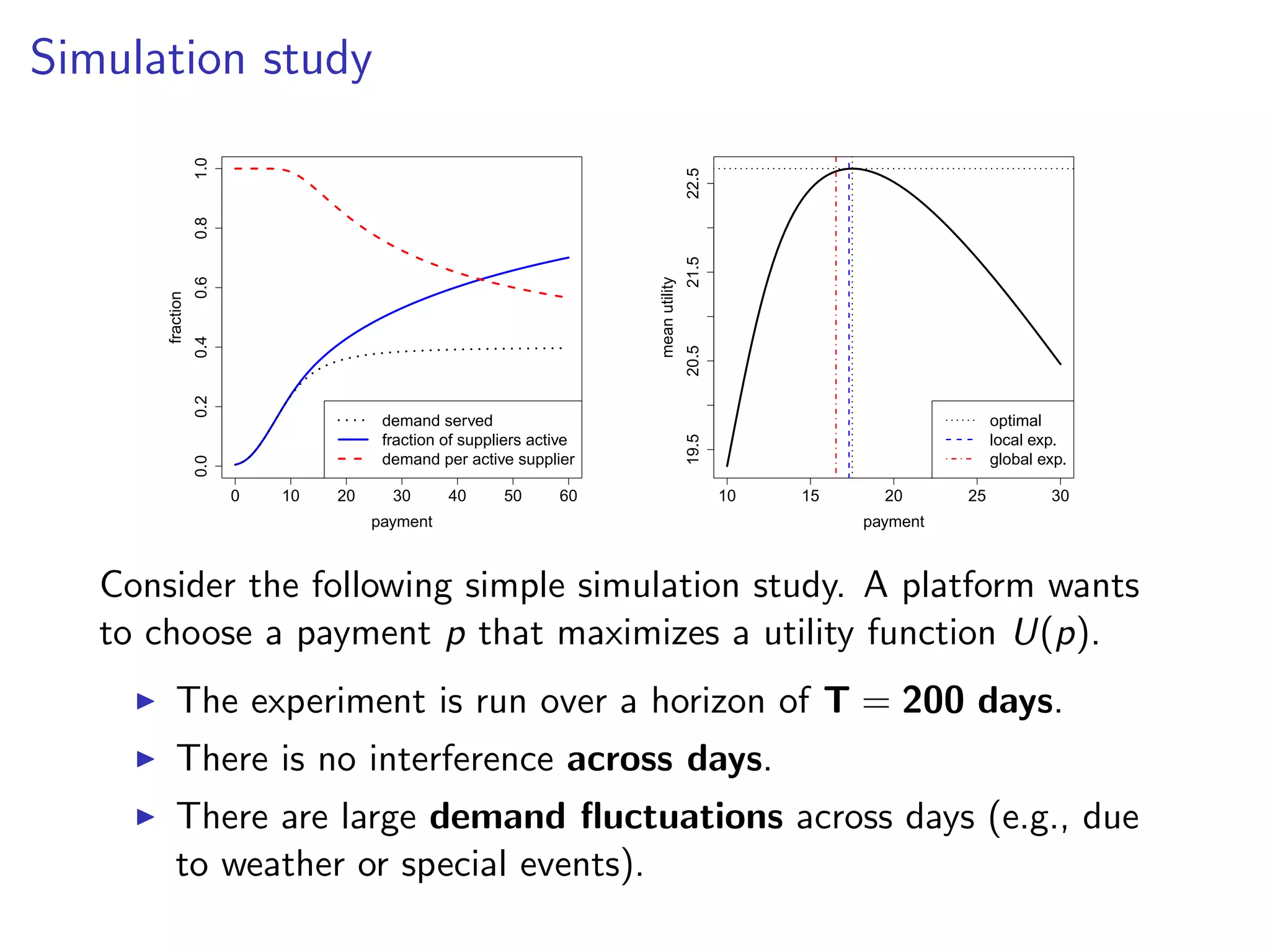
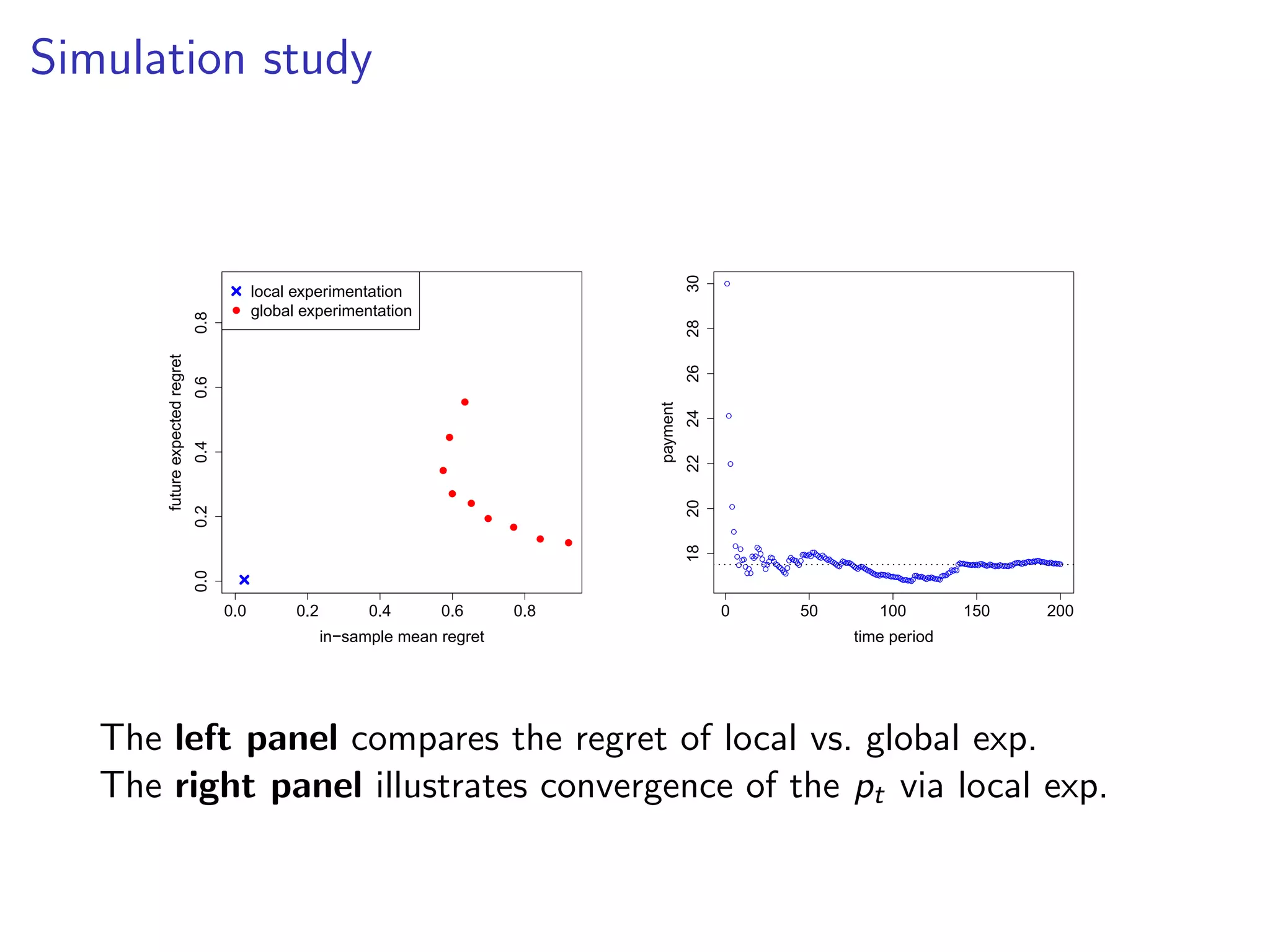
This document discusses challenges and strategies in optimizing payment structures for workers in sharing economy platforms through experimentation. It explores interference effects and proposes a local experimentation approach to efficiently estimate the marginal response of workers to payment changes while correcting for demand cannibalization. Simulation studies highlight the effectiveness of this method compared to traditional global experimentation in improving utility over time.

1. Experimenting in Equilibrium
Stefan Wager
Stanford University
SAMSI Causal Inference
Duke, NC, 9 December 2019
joint work with Kuang Xu

2. Modern computational infrastructure enables us to routinely and
quickly run large-scale data analyses, and has led to a resurgence
of interest in experimental design.
Many companies, ranging from pharmaceuticals to “traditional”
tech, invest heavily in running multiple randomized trials to
optimize their products.
In recent years, we’ve seen the rise of platforms that support
miniature economies. Experimentation in this setting is harder.

3. Motivating Example
The following is a toy version of a problem that comes up with
sharing economy platforms:
A platform wants to satisfy demand using freelance workers.
Each day, the platform commits to a payment pi delivered to
worker i for each unit of demand served.
On seeing the offered pi , each worker decides to become
“active” or not.
Demand is randomly allocated among workers who are active
and are not already busy.
The platform and workers have divergent 1-st order preferences:
Workers would prefer high payment and few active workers.
Platform would prefer low payments and many active workers.
Question: How can we set the payments to optimize utility?

4. Motivating Example
Question: How can we set the payments to optimize utility?
Idea 1: Run a case-control randomized trial, give different
workers different payments.
This won’t work because of interference. Workers who are
paid more are more likely to become active, and cannibalize
demand from others.

5. Motivating Example
Question: How can we set the payments to optimize utility?
Idea 1: Run a case-control randomized trial, give different
workers different payments.
This won’t work because of interference. Workers who are
paid more are more likely to become active, and cannibalize
demand from others.
Idea 2: Run a randomized trial on non-interfering workers.
But all workers interfere with each other. In principle, you
could randomize across cities, at the cost of loss of power.

6. Motivating Example
Question: How can we set the payments to optimize utility?
Idea 1: Run a case-control randomized trial, give different
workers different payments.
This won’t work because of interference. Workers who are
paid more are more likely to become active, and cannibalize
demand from others.
Idea 2: Run a randomized trial on non-interfering workers.
But all workers interfere with each other. In principle, you
could randomize across cities, at the cost of loss of power.
Idea 3: Model and correct for interference?
In a large sample mean-field limit, we may be able to
understand quite well how interference works.

7. Interference
When experimenting in a marketplace, interference is ubiquitous.
In statistics, the classical approach to interference starts from
cutting up the exposure graph (Aronow and Samii, 2017; Athey,
Eckles and Imbens, 2018; Basse, Feller and Toulis, 2019; Hudgens
and Halloran, 2008; Leung, 2019; Manski, 2012; Sobel, 2006).
Main question: Can we design more powerful experiments that are
robust to interference using a little bit of modeling instead.

8. Key Assumption: Workers respond to expected revenue
In order to correct for interference, our core assumption is that all
interference is mediated by driver response to expected revenue.
Strong assumption, but aligned with empirical evidence in the
ride sharing context (Hall, Horton and Knoepfle, 2019).
As with the sufficient statistics approach in economics (Chetty,
2009), we don’t specify a full model and instead just rely on some
simple relationships.

9. Key Assumption: Workers respond to expected revenue
In order to correct for interference, our core assumption is that all
interference is mediated by driver response to expected revenue.
Strong assumption, but aligned with empirical evidence in the
ride sharing context (Hall, Horton and Knoepfle, 2019).
As with the sufficient statistics approach in economics (Chetty,
2009), we don’t specify a full model and instead just rely on some
simple relationships.
=⇒ All interference is due to demand cannibalization, and
mediated by total supply.

10. A simple model
In order to correct for interference, we assume the following model:
The platform chooses a distribution π, and promises a
payment Pi
iid
∼ π to each worker.
If a fraction µ of workers are active, the expected amount of
demand served by any worker if they become active is q(µ).
Workers have random outside options Bi such that, given
the distribution π, the i-th worker is active with probability
fBi
(pi q(µ(π))) = 1/ (1 + exp [−β (pi q(µ(π)) − Bi )]) .
Note: the expected revenue of the i-th worker is pi q(µ(π)).
The system is in equilibrium, i.e., the fraction of active
workers is µ(π) = E [fBi
(pi q(µ(π)))].

11. Key Idea: A local experiment
We start by running an experiment where we independently
perturb each works payment by a small random amount:
pi = p + ζεi , εi
iid
∼ {±1} .
Under reasonable assumptions, local experimentation does not
alter total supply, and so does not lead to any interference.

12. Key Idea: A local experiment
We start by running an experiment where we independently
perturb each works payment by a small random amount:
pi = p + ζεi , εi
iid
∼ {±1} .
Under reasonable assumptions, local experimentation does not
alter total supply, and so does not lead to any interference.
Write Zi for whether the i-th worker gets active, and estimate
∆ ←
1
ζ
OLS (Zi ∼ εi )
for the marginal response ∆ of workers to changes in p.
The marginal response function is not of direct policy interest in
itself, because it ignores cannibalization effects.
But given our key assumption, knowing ∆ gets us a long way
towards answering policy-relevant questions.

13. Simulation study
0 10 20 30 40 50 60
0.00.20.40.60.81.0
payment
fraction
demand served
fraction of suppliers active
demand per active supplier
10 15 20 25 30
19.520.521.522.5
payment
meanutility
optimal
local exp.
global exp.
Consider the following simple simulation study. A platform wants
to choose a payment p that maximizes a utility function U(p).
The experiment is run over a horizon of T = 200 days.
There is no interference across days.
There are large demand fluctuations across days (e.g., due
to weather or special events).

14. Simulation study
The platform considers the following experimental strategies:
Global experimentation: Each day up to T deploy a shared
random price pt and observe the realized utility Ut. At time
T, fit a spline Ut ∼ pt and deploy the max thereafter.
Local experimentation: Estimate ∆ via price perturbations
pit = pt + ζεit. Obtain an estimate of dU(p)/dp that
accounts for interference. Update pt+1 via gradient descent.

15. Simulation study
0.0 0.2 0.4 0.6 0.8
0.00.20.40.60.8
in−sample mean regret
futureexpectedregret
q
q
q
q
q
q
q
q q
q
local experimentation
global experimentation
q
q
q
q
q
q
q
q
q
qq
q
q
q
q
qqq
qq
q
q
q
q
qq
qq
qqqqqqqq
q
qqqqqqq
q
qqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqq
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq
0 50 100 150 200
18202224262830
time period
payment
The left panel compares the regret of local vs. global exp.
The right panel illustrates convergence of the pt via local exp.

16. Mean-field analysis
We adopt an asymptotic setting with n → ∞ workers who could
potentially become active.
Assumption 1: Workers observe a daily state variable A that
allows them to anticipate demand,
lim
n→∞
E |D/n − dA| A = a = 0.
I’ll implicitly condition on a everywhere, and use an a-subscript to
remind us of this.
Assumption 2: The “marketplace dynamics” are scale-invariant:
If there are D units of demand and T = n
i=1 Zi active workers, Ω
units of demand get served, where Ω/T ≈ ω(D/T) for large n,
and ω(·) is a known regular allocation function (taken to be
smooth, concave, non-decreasing, etc.)

17. A simple model
In order to correct for interference, we assume the following model:
The platform chooses a distribution π, and promises a
payment Pi
iid
∼ π to each worker.
If a fraction µ of workers are active and conditionally on daily
state A = a, the expected amount of demand served by
any worker if they become active is qa(µ).
Workers have random outside options Bi such that, given
the distribution π, the i-th worker is active with probability
fBi
(pi q(µ(π))) = 1/ (1 + exp [−β (pi q(µ(π)) − Bi )]) .
Note: the expected revenue of the i-th worker is pi q(µ(π)).
The system is in equilibrium, i.e., the fraction of active
workers is µa(π) = E fBi
(pi qA(µ(π))) A = a .
NB: The distribution of outside options Bi may depend on state A.

18. Mean-field analysis
We adopt an asymptotic setting with n → ∞ workers who could
potentially become active.
Fact 1: Given the choice of payment distribution π, an
equilibrium with µa(π) = E fBi
(pi q(µA(π))) A = a exists and is
unique. The number of active workers has a binomial(µa(π), n)
distribution.
Fact 2: As n → ∞, the equilibrium (and relevant derivatives)
converge to a mean-field limit.

19. Mean-field analysis
Fact 3: Recall our local experiment where we independently
perturb each worker’s payment by a small random amount,
pi = p + ζnεi , εi
iid
∼ {±1} .
Write Zi for whether the i-th worker gets active, and estimate
∆ ←
1
ζn
OLS (Zi ∼ εi ) .
Then, if ζn → 0 and ζn
√
n → ∞,
∆ →p ∆a(p) = q(µa(p))E fBi
(pq(µA(p))) A = a ,
and we refer to ∆a(p) as the marginal response function.

20. Mean-field analysis
Fact 4: Under out assumptions, the marginal response function
∆ and the supply response dµ(p)/dp are linked via the system
dµa(p)
dp
= ∆a(p) − p∆a(p)
da
µ2
a(p)
ω (da/µa(p))
ω(da/µa(p))
dµa(p)
dp
.
Apart from ∆(p), all other quantities in this equation, da and
µa(p), can be readily observed.
Theorem. The local experimentation strategy outlined above
consistently recovers dµa(p)/dp as n → ∞.

21. Learning via Local Experimentation
The ultimate goal of the platform is to maximize its utility U, for
our purposes taken as total cost minus total revenue.
Write γ for the platform’s revenue per unit of demand served. In
the mean-field limit, the utility then converges to
n−1
Ua(p) = (γ − p) ω(da/µa(p)) µa(p), U(p) = E [UA(p)] .
Once we know dµa(p)/dp, working out the utility derivative
dUa(p)/dp amounts to calculus.
We consider a platform that uses these estimates to optimize U(p)
by gradient descent (or rather ascent).

22. A First-Order Algorithm
We now proceed to optimize payments via a variant of mirror
descent Specify a step size η, an interval I = [c−, c+], and an
initial payment p1. Then, at time period t = 1, 2, ...:
1. Deploy randomized payment perturbations εit around pt.
2. Estimate ∆ by regressing market participation on εit.
3. Translate this into an estimate Γt of dUAt (p)/dp via the
transformation implied by the mean-field limit.
4. Perform a gradient update, where θt = t
s=1 sΓs:
pt+1 = argminp
1
2η
t
s=1
s(p − ps)2
− θtp : p ∈ I
If the Ua(p) functions are strongly concave, this attains a 1/t rate
of convergence in large markets, both in regret and squared error.

23. A First-Order Algorithm
If the Ua(p) functions are strongly concave, this attains a 1/t rate
of convergence in large markets, both in regret and squared error.
Theorem. If the Ua(p) functions are σ-strongly concave,
|ua(p)| ≤ M, and we use a step size η > σ−1 then
lim
n→∞
P
1
T
T
t=1
t (UAt (p) − UAt (pt)) ≤
ηM2
2
= 1,
for any fixed payment p ∈ [c−, c+].
Corollary. If in addition the day-specific states At are IID, then
lim sup
n→∞
P (p∗
− ¯pT )2
≤
ηM2
σT
16 log δ−1
+ 4 ≥ 1 − δ,
p∗ = argmax {E [UA(p)] : p ∈ I} and ¯pT = 2
T(T+1)
T
t=1 t pt.

24. Comparison with global experimentation
Conceptually, our problem is closely related to the literature on
continuous-armed bandits, motivated by the following setting:
In each time period, the analyst deploys pt, and observes a
reward Ut = U(pt) + noise.
We want to control regret T−1 T
t=1 (U(p∗) − U(pt)).
Some references include Bubeck et al. (2017), Flaxman et al.
(2005), Kleinberg (2005) and Shamir (2013).
The optimal regret in this problem scales as 1/
√
T, even if we
know U(p) is quadratic (Shamir, 2013).

25. Comparison with global experimentation
Here, instead, the gradients we get via our approach enable a 1/T
rate of convergence.
In other words, if local experimentation is applicable it
fundamentally changes the difficulty of the problem relative to
the continuous-armed bandits setting.
The gain from local experimentation is comparable to the gain we
could get from running two function evaluations with the same
noise (Duchi et al., 2015).

26. Extensions via generalized earning functions
The core assumption that enables our approach is that workers
care only about expected revenue, and thus respond to payments
pi and market-level congestion q(µa(π)) via their product.
Then, we showed that the mean-field limit is characterized by the
following balance condition.
µa(π) = E fBi
(pi q(µA(π))) A = a .
The form of this balance condition is crucial: If fB can have a
generic dependence on pi and q, we may run into intractable
difficulties.

27. Extensions via generalized earning functions
One way to generalize this setting is to let workers respond to pi
and q via a (known) generalized earning function (GEF) θ,
µa(π) = E fBi
(θ(pi , q(µA(π)))) A = a .
Example: Risk aversion. Workers respond to the expectation of
a concave function of revenue. In the binary case where each
worker serves 0 or 1 units of demand, we get θ(p, q) = β(p)q for
some concave β(·).
Example: Supply-side surge pricing. The platform commits to
paying the i-th worker s(D/T)pi for some increasing surge
multiplier s(·). Surge is automatic and anticipated by workers.
With surge, the mean-field limit of expected revenue of the i-th
worker is θ(p, q) = pqs(ω−1(q)).

28. Extensions via generalized earning functions
One way to generalize this setting is to let workers respond to pi
and q via a (known) generalized earning function (GEF) θ,
µa(π) = E fBi
(θ(pi , q(µA(π)))) A = a .
With GEF, the balance condition implies that a marginal
response function can be estimated via local perturbations:
∆a(p) = pθ(p, q(µa(p)))E fBi
(θ(p, q(µA(p)))) A = a .
Then, dµa(p)/dp can be linked to ∆a(p) via a linear system that
depends on system dynamics, thus enabling local experimentation:
dµa(p)
dp
= p + q (µa(p))
dµa(p)
dp
q θ(p, q(µa(p)))
E fBi
(θ(p, q(µA(p)))) A = a .
NB: The above are conjectures; no formal results yet with GEF.

29. Simulation study: surge pricing
0.0 0.2 0.4 0.6 0.8
0.00.20.40.60.8
in−sample mean regret
futureexpectedregret
q
q
q
q
q
q
q
q q
q
local experimentation
global experimentation
0.0 0.2 0.4 0.6 0.8
0.00.20.40.60.8
in−sample mean regret
futureexpectedregret
q
q
q
q
q
q
q q
q
q
local experimentation
global experimentation
The left panel is the simulation experiment from the beginning.
The right panel shows results with an extension of our method
that allows for surge pricing.

30. Most work on experimental design assumes no interference, but
this assumption often fails in a marketplace setting.
We showed, however, that in some cases we can correct for
interference with better power using some light-weight modeling.
exposure graph mechanism
graph cutting sparse and known arbitrary
model based complete mean-field game
There are more open questions than closed ones.

31. Thanks!