The document appears to be notes from a summer school mathematics class. It includes discussions of various mathematical concepts like infinite series, rates of reactions, geometric sequences, Taylor series, and Euler's formula. Students are asked to consider what the most beautiful mathematical formula is and why. Equations like the sum of a geometric series and the derivation of Euler's formula are shown. Overall, the document covers a wide range of mathematical topics through examples, questions, and discussions of concepts like beauty and imagination in mathematics.

1. May 25, 2016
Summer School
I A C S
112/28/2018

2. A three fold challenge
Yet in another School ?
Moreover, in Summer ?
More-moreover in a
Post-Lunch Session ?
212/28/2018

3. 312/28/2018

4. What is
COMMON
among the
images?
412/28/2018

5. 512/28/2018

6. 612/28/2018

7. 712/28/2018

8. 812/28/2018

9. 912/28/2018

10. 1012/28/2018

11. 1112/28/2018

12. 1212/28/2018

13. They are Beautiful,
the Most Beautiful …
1312/28/2018

14. ‘all mathematics is beautiful, yet
some is more beautiful than the
other’
paraphrasing George Orwell
1412/28/2018

15.  What is the most beautiful formula?
 How and Why is it Most Beautiful?
 How and why something is Beautiful?
 A Few Remarks on Mathematics, Mathematicians,
and Formula…
1512/28/2018

16.  The moving power of mathematical invention is
not reasoning but imagination.
Augustus de Morgan
 Imagination is more important than knowledge.
Albert Einstein
How can it be that mathematics, being after all a
product of human thought independent of experience,
is so admirably adapted to the objects of reality?
Albert Einstein 1612/28/2018

17.  There is no branch of mathematics,
however abstract, which may not some
day be applied to phenomena of the real
world.
Nikolai Lobatchevsky.
 A mathematician is a blind man in a
dark room looking for a black cat which
isn’t there.
 Charles Darwin.
1712/28/2018

18. Lt y →xU = 1 ; Buddhahood (enlightened)
y → x is “Human Revolution”,
“Casting off the transient and Revealing the True”.
LIFE
A philosophical Version of the Mathematical Identity
U = x/y y = Bodhisattva, x = true identity
“Yui Butsu, Yo Butsu”
1812/28/2018

19. 1912/28/2018

20.  Does an infinite series necessarily have a finite Answer?
 Convergence
 S = ?
S = 1+x +x2 +x3+ . . .+xn-1 + xn
S.x= x+ x2 +x3 +. . . + xn +xn+1
S.(1-x) = 1 - xn+1
S = (1 – xn+1)/(1-x)
S => 1/(1-x) [since xn+1 =0 for large n]
Check it using calculator and see the convergence
2012/28/2018

21. 2112/28/2018

22. 2212/28/2018

23. The hare and the tortoise
decide to race
2312/28/2018

24. Since I run twice as fast as you do, I
will give you a half mile head start.
Thanks!
2412/28/2018

25. ½ ¼ 8
1
16
1
2512/28/2018

26. ½ ¼ 8
1
16
1
The hare quickly reaches the turtle’s
starting point – but in that same time
The turtle moves ¼ mile ahead.
2612/28/2018

27. ½ ¼ 8
1
16
1
By the time the rabbit reaches the
turtle’s new position, the turtle
has had time to move ahead.
2712/28/2018

28. ½ ¼ 8
1
16
1
No matter how quickly the hare
covers the distance between himself
and the turtle, the turtle uses that
time to move ahead.
2812/28/2018

29. ½ ¼ 8
1
16
1
Can the hare ever catch the
turtle???
2912/28/2018

30. 1+1/2 +1/4 +1/8 + . . . ?
3012/28/2018

31. 3112/28/2018

32. 3212/28/2018

33. 1 mile 2 miles
1+1/2 +1/4 +1/8 + . . . = 2 ???
3312/28/2018

34. let x = ½
S = 1+1/2 +1/4 +1/8 + . . .
S = 1/(1-x) = 1/(1- ½) = 1/(1/2) = 2
3412/28/2018

35. 1 mile 2 miles
3512/28/2018

36. 3612/28/2018

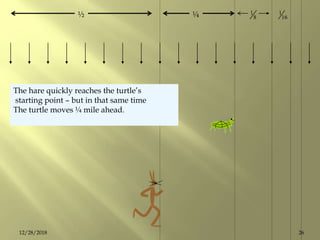
37.  A zeroth order reaction [At = A0 - k t ]
 t1/2 = f(? ? ?) [ half-life time]
= A0 /(2k) [k = rate constant]
 tcomp = A0 / k [completion time]
 A0 → A0 /2 → A0 /4 → A0 /8 → → → zero
 tcomp = t1 + t2 + t3 + …
 A0 / k = A0 /2k + A0 /4k + A0 /8k + …
 A0 / k = (A0 /k) (1/2 + 1 /4 +1 /8 + … )
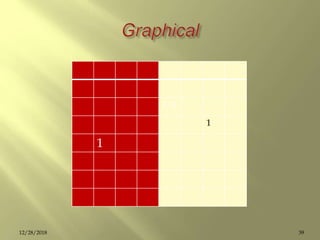
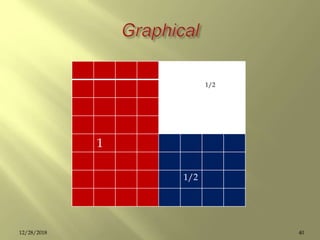
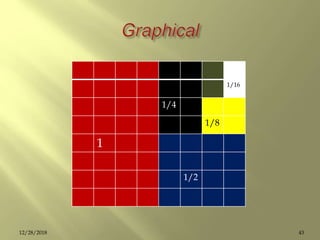
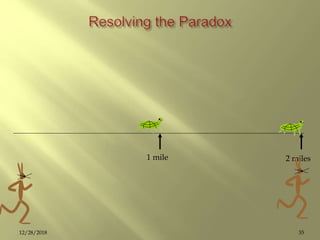
 1 = (1/2 + 1 /4 +1 /8 + … )
 2 = (1+ 1/2 + 1 /4 +1 /8 + … )
3712/28/2018

38.  A zeroth order reaction [At = A0 - k t ]
 tƟ = f(? ? ?) [ half-life time]
= A0 /(2k) [k = rate constant]
 tcomp = A0 / k [completion time]
 A0 → A0 /2 → A0 /4 → A0 /8 → → → zero
 tcomp = t1 + t2 + t3 + …
 A0 / k = A0 /2k + A0 /4k + A0 /8k + …
 A0 / k = (A0 /k) (1/2 + 1 /4 +1 /8 + … )
 1 = (1/2 + 1 /4 +1 /8 + … )
 2 = (1+ 1/2 + 1 /4 +1 /8 + … )
3812/28/2018

39. 1/4
1
1
3912/28/2018

40. 1/2
1/4
1
1/2
4012/28/2018

41. 1/4
1/4
1
1/2
4112/28/2018

42. 1/8
1/4
1/8
1
1/2
4212/28/2018

43. 1/16
1/4
1/8
1
1/2
4312/28/2018

44. 1/16 1/32
1/32
1/4
1/8
1
1/2
4412/28/2018

45. Physicist Richard Feynman wrote in his
notebook in bold scrawl, when he was
fifteen.
4512/28/2018

46.  Kanser and J. Newman, in Mathematics and the
Imagination.
4612/28/2018

47.  A discovery of the
remarkable connection
between the
exponential and the
trigonometric functions,
by all time great
Mathematician,
Euler.
 Euler was a great
experimental
mathematician.
 He played with
formulas like a
child playing
with toys.
4712/28/2018

48. 4812/28/2018

49. Can I expand an arbitrary function f(x) around x=a
as an infinite series?
f(x) =c0 + c1(x-a) +c2(x-a)2 + c3(x-a)3+ . . .+cn (x-a)n ;
But how to get all those {ci}?
4912/28/2018

50. f(x) =c0 + c1(x-a) +c2(x-a)2 + c3(x-a)3+ . . .+cn (x-a)n ;
at x=a,
f(a) = c0
f’ (x) = c1 + 2c2 (x-a) + 3c3 (x-a)2 + . . . + ncn (x-a)n-1 ;
fˊ (a) = c1
f’’ (x) = 2c2 + 3.2c3 (x-a) + . . .+ n(n-1)cn (x-a)n-2 ;
fˊˊ(a) = 2c2 
fˊˊ(a)/2 = c2
fˊˊˊ(a) = 3.2.c3  c3 = fˊˊˊ(a) / 3.2 or
fˊˊˊ(a) /3! = c3
5012/28/2018

51. f(x) =c0 + c1(x-a) +c2(x-a)2 + c3(x-a)3+ . . .+cn (x-a)n ;
at x=a,
f(a) = c0
fˊ (a) = c1
fˊˊ(a)/2 = c2
fˊˊˊ(a) /3! = c3
Similarly …
f(n)(a) /n! = cn
5112/28/2018

52. Thus we get the Taylor’s series
f(x) =c0 + c1(x-a) +c2(x-a)2 + c3(x-a)3+ . . .+ cn (x-a)n ;
with Cn = f(n)(a) /n!
f(x) = f(a) + (x-a) fˊ (a) + {(x-a)2/2!} fˊˊ(a)
+ {(x-a)3/3!} fˊˊˊ(a) + . . .;
take a=0, to get the Maclaurin Series:
f(x) = f(0) + x fˊ (0) + (x2/2!) fˊˊ(0) + (x3/3!) fˊˊˊ(0) + . . .
5212/28/2018

53. 5312/28/2018

54. Example 2
f(x) = f(0) + x fˊ (0) + (x2/2!) fˊˊ(0) + (x3/3!) fˊˊˊ(0) + . . .
f(x)= sin(x) = x - x3/3! + x5/5! – x7/7! + x9/9! - …
5412/28/2018

55.  Replacing x by iy is like playing with meaningless
symbols, but Euler had enough faith in his formula to
make it meaningful. Thus we get,
eiy = 1 + iy - y2/2! - iy3/3! + y4/4! + iy5/5! - y6/6! – iy7/7! + …
5512/28/2018

56. 5612/28/2018
eiy = 1 + iy - y2/2! - iy3/3! + y4/4! + iy5/5! - y6/6! – iy7/7! + …
eiy = (1 - y2/2! + y4/4! - y6/6! + …) +
i (y - y3/3! + y5/5! - y7/7! + …)

57.  eiy = 1 + iy - y2/2! - iy3/3! + y4/4! + iy5/5! - y6/6! – iy7/7! +
eiy = (1 - y2/2! + y4/4! - y6/6! + …) +
i (y - y3/3! + y5/5! - y7/7! + …)
 sin(x) = x - x3/3! + x5/5! – x7/7! + x9/9! - …
 cos(x) = 1 - x2/2! + x4/4! – x6/6! + x8/8! - …
eiy = cos (y) + i sin(y), similarly e-iy = cos (y) - i sin(y)
Take y = π,
eiπ = cos (π) + i sin(π) = -1 + 0
eiπ = -1 5712/28/2018

58.  It involves three most important mathematical operations,
namely
 addition,
 multiplication and
 exponentiation.
 It connects the five most important constants in
mathematics:
e, π, i, 0 and 1.
5812/28/2018

59.  It includes four major branches of classical
mathematics:
 arithmetic (through 0 and 1 ),
 algebra (by i),
 geometry (by π), and
 analysis (by e).
5912/28/2018

60. A Home Task
π/4 = 1 – 1/3 +1/5 -1/7 +1/9 - …
6012/28/2018

61. 1. Use eiπ = -1 = i2 to prove ln i = iπ/2;
4. evaluate ln(1+ i) – ln(1- i) = 2 i (1 – 1/3 +1/5 -1/7 + 1/9 - …)
5. manipulate to have ln {(1+i)/(1-i)} = ln i
6. equate (4) and (5) to get ln i = 2 i (1 – 1/3 +1/5 -1/7 + 1/9 - …)
7. equate (1) and (7) to find
π/4 = 1 – 1/3 +1/5 -1/7 +1/9 - …
Enough Hints
6112/28/2018

62. eiπ = -1 = i2 Solution
ln eiπ = ln i2
iπ = 2 ln i
ln i = iπ/2;
ln(1+ i) – ln(1- i) = 2 i (1 – 1/3 +1/5 -1/7 + 1/9 - …)
ln{(1+i)/(1-i)} = ln{(1+i)(1+i)/(1-i)(1+i)}
= ln(1+i2+ 2i)/(1- i2)=ln(2i/2) = ln i
So, ln i = 2 i (1 – 1/3 +1/5 -1/7 + 1/9 - …)
Or, i π/2 = 2 i (1 – 1/3 +1/5 -1/7 +1/9 - …)
π/4 = 1 – 1/3 +1/5 -1/7 +1/9 - …
6212/28/2018

63. Often we say, Simple is beautiful. If
it’s so, then the formula must be
beautiful.
6312/28/2018

64. 6412/28/2018

65. if you like to relate
beauty with
usefulness and significance,
then also we must say:
The formula is beautiful.
6512/28/2018

66.  The most beautiful is
something lying in
repaying the debt of Gratitude.
6612/28/2018