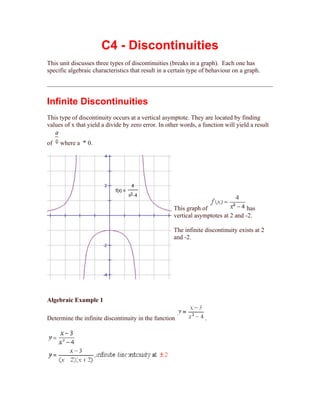
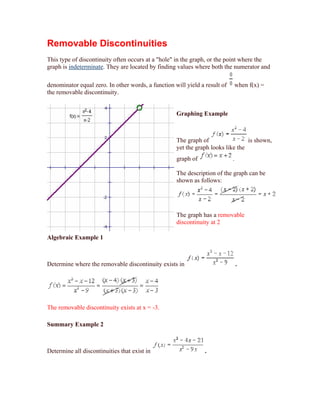
This document discusses three types of discontinuities in graphs: infinite discontinuities which occur at vertical asymptotes, jump discontinuities where the graph "jumps" between values, and removable discontinuities which appear as "holes" in the graph. Infinite discontinuities are found where functions yield division by zero errors. Jump discontinuities occur where the absolute value of a function changes signs. Removable discontinuities are located where both the numerator and denominator equal zero. Examples are provided to demonstrate identifying each discontinuity type algebraically.

1. C4 - Discontinuities
This unit discusses three types of discontinuities (breaks in a graph). Each one has
specific algebraic characteristics that result in a certain type of behaviour on a graph.
Infinite Discontinuities
This type of discontinuity occurs at a vertical asymptote. They are located by finding
values of x that yield a divide by zero error. In other words, a function will yield a result
of where a 0.
This graph of has
vertical asymptotes at 2 and -2.
The infinite discontinuity exists at 2
and -2.
Algebraic Example 1
Determine the infinite discontinuity in the function .

2. Algebraic Example 2
Determine the infinite discontinuity in the function .
Jump Discontinuities
This type of discontinuity is typically a step function, where the graph "jumps" from one
step to another.. They are located by finding values of x wher the absolute value of a
function changes from positive to negative.
This graph of becomes
The jump discontinuity occurs where
the function steps up from -1 to 1, at 3
Algebraic Example
.

3. Removable Discontinuities
This type of discontinuity often occurs at a "hole" in the graph, or the point where the
graph is indeterminate. They are located by finding values where both the numerator and
denominator equal zero. In other words, a function will yield a result of when f(x) =
the removable discontinuity.
Graphing Example
The graph of is shown,
yet the graph looks like the
graph of .
The description of the graph can be
shown as follows:
The graph has a removable
discontinuity at 2
Algebraic Example 1
Determine where the removable discontinuity exists in .
The removable discontinuity exists at x = -3.
Summary Example 2
Determine all discontinuities that exist in .

4. A removable discontinuity exists at x = -3.
An infinite discontinuity exists at x = 0 and x = 3.