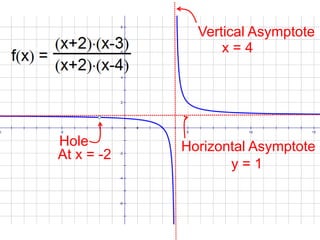
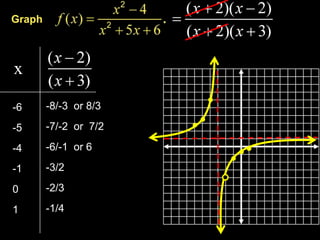
This document discusses key concepts for graphing rational functions: 1) Vertical and horizontal asymptotes are determined by factors in the denominator that do or do not cancel out. A vertical asymptote is indicated at x = -3 and there is a hole at x = -2. 2) The horizontal asymptote is the line y = 1. 3) Examples are provided to demonstrate graphing rational functions based on identifying discontinuities and asymptotes.

1. Vertical Asymptotex = 4HoleHorizontal AsymptoteAt x = -2y = 1

2. Graphing rational functionsFactor numerator and denominatorDiscontinuities occur where denominator equals zeroHoles are indicated by factors of denominator that cancel out

3. Vertical asymptotes are indicated by factors of denominator that do not cancelHorizontal Asymptotes (predict end behavior) – look at highest degree term of numerator and denominatorDegree of top > degree of bottom: no HA

4. Degree of top < degree of bottom: HA is y = 0

5. Degrees equal: HA is y = Determine the equations of any asymptotes and the values of x for any holes in the graph of Undefined for x = –2 and –3Hole at x = -2Vertical asymptote is the line x = -3Horizontal asymptote: the line y = 1 Example 3-1a

6. GraphVA: x = -3HA: y = 1Hole at x = -2(-2, -4)-2= -4-2

7. Graphx-8/-3 or 8/3-7/-2 or 7/2-6/-1 or 6-3/2-2/3-1/4-6-5-4-101

8. GraphVA: x = –1No holesHA: y = 1Example 3-2a

9. GraphExample 3-2b