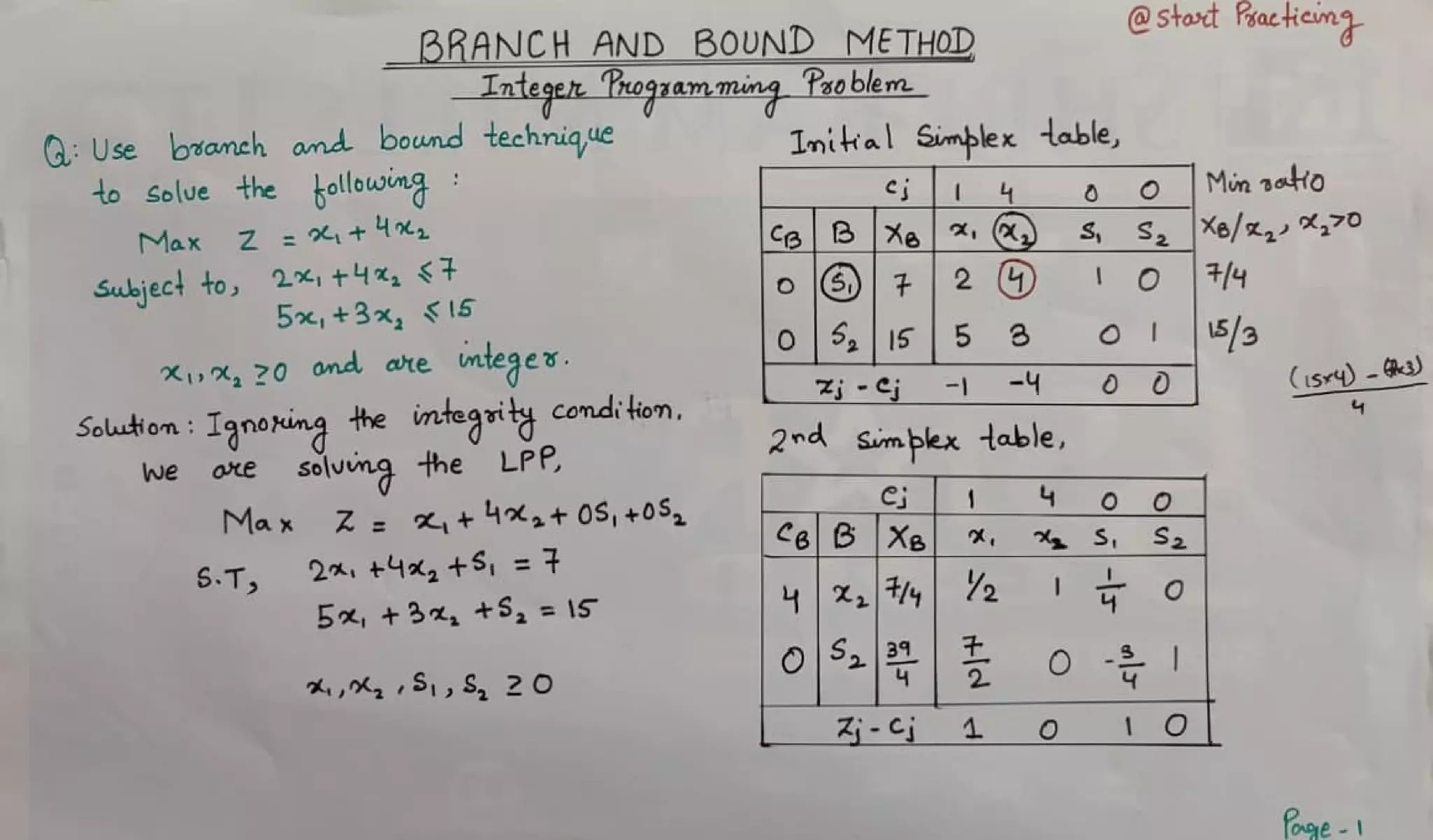
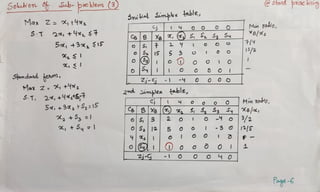
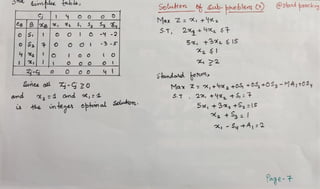
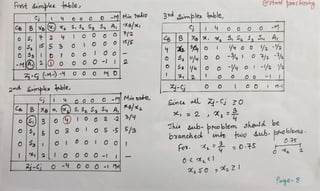
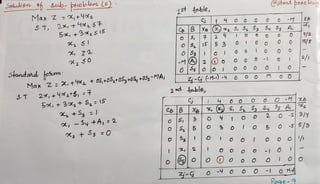
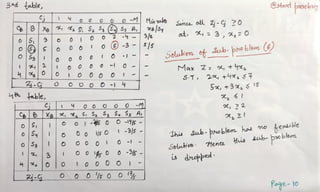
The document describes using the branch and bound technique to solve an integer programming problem. The problem is broken into 5 sub-problems. Sub-problems 1, 2, and 3 are solved, with optimal solutions of x1=2, x2=2 for sub-problem 1; x1=1, x2=2 for sub-problem 2; and x1=1, x2=0 for sub-problem 3. Sub-problems 4 and 5 are not feasible. The best overall integer solution is x1=1 and x2=2, with an optimal objective value of 5.

1. @Stoxt acHieun2
BRANCH AND BOUND METHOD
Lnteger rogxam ming faoblem
G: Use branch amd bound techriaue
to Solue the tollououng
Inital Simplex table,
Min oto
Max Z =+ 4*2
Subject to, 2 +4 $t
5%,+3x, S15
Ce B Xe s, S2 Xe/,,70
2
o5 15 5 8
/4
K1u 20 ond ae mteger.
Z-Ci -4 1 5 -
Solution: Ianoting the integity comditiom
soluung he LPP,
Z = Z+ 4 t 0S +05,
2 4xa +5, = 4
2 nd Sumplex Hable,
we ae
Ma x
S, S2
S.T
5, +3, +S2 = 1S 4
o o
a S1, S 20
Z-Cj 4 0_1 O|
oe

2. @slotprachicing
Sub-problem(2)
Sunce all Zj-C 70 Siub-problem(1)
o btoumed
An obtmal
soukion is
at
Max Z , +4%2 Max Z: d+9
ST, 2 +4, <4
0 .75
Max 7 +
5x, +3 $ 15
5+3,s15
, 22.
Jhis problem should be brane hed
into o sub-pso blems
Fov,
2 2
1 2 2 2
Apblng ese tuwo conditions spesoty
in ha ven
LPP we get two sub-problems
Poge-

3. Staitt POCHO
SolukionoSub- poblm (4)
Fist Sumplex teble,
Max 2= Ki
+4a
S.T, 2x, +4 t
5a, +3a & 15
1
O Mn roto
S s
/4
o S, 7 2
o S| IS5 O1S/3
o oI 1
Standard bewm
Z -
Max z +ya+ 0S, +0S,+0S3
2,+ tS, *
5, +3 + S 155
+$3 = 1
274 able,
ST
C 4 0 o 0N 1ako,
Cs BXa S S2 S|Ke/%
O 4 3/2
I-3 1|s
o3. 2 5
4 o
Poge-3

4. 35d 4able, @stabd b3acm
Sub-paoblem(9) Sub. problem (
40 0
Se BXe S S, S3|
| 3/a o V2 -2
oS/ao o -5/a
Max Z +Y
S.T, 2, +4, S7
5+3 SI5
Max Z- % +4d2
S T, 2x, +4*, 3+
2 S1
Z-Ci o a o 2 , 1 2 2.
Sunee all -Cj 2o a
Sub pro blem shsuld be
two sub- problems
Jhis
bxan hed vmto
Fo 'S
I < , 2
s1, *,22
Page-4

5. Solukon oSub-boblm (2) @shoret bxackeing
2m table
Max Z 7,+42
S.T, 2+ <t+
5 +3 15
a 2
Ca BXsX 2 S S S A
4 / 4 a 4 o o
o
Standahd borm, A Y -2 -y -I
Max Z x, +Y«,t 0Si t08 +0S,-MA,
2% 4 +S, =*
5x, +3x +S2 1S
-S2 t+Ai = 2
Snca oll i-g 20 bd,
ST
am ai hicial vau able A Um fhe
basis ts at bosite devel
Sni Hal Simplex table, solukon .
no heasi ble
Sub-poblem is
Thee exsis
drspped
St, Ihis
o72
155
A 2
3
o -12/Y1
L3- (M) 0 0 MO

6. Sokuh on Sub-broblem (3) @Stot OC
Sniial Simphx table,
Max Z t4x2
0 0 0 0
Ce BXe S S, Sa S
Min gado,
B/2
S T 2, +4* $+
5 +3x S1s
15/3
Stemdord koxm,
Max Z +9«2
S.T, 2%, +4,t5t
5, +3 tS, = 15
2md Simples table,
Min soo,
o S3 2 0 IO-1 o
9/2
+Sy =I o S12 I-3 o 12S
5
Poge-6

7. Aumblax tab
Soluton 6 Sub- broblem @Shoad brocheg
o S o O o --2
o S
Max Z 1 +|%a
S.T, 24+4 < t
5 t3 I5
oo 3 5
O 000L 72
Stomdord tom
Max Z +4d2+0S, +0S+0Sg -MAjt0Sy
S.T 2, +Y*2 +S: +
5%, +3x +S2 =l5s
2+Sg
Sunce oll -9 20
amd 1 and o«,:i
t h e intege optnal Solukon.
Sy +A,:2
age-F

8. Rst &implaz table, Cstod backeng
4 0 0 0 0 -M Mintuko
Ce B Xe S S, Sg S Ae/
oS, 7|24I o o o t/2
|S|155 3 0 o o o 5/s
S3 D O o 00
-M2O o o o 0 -1
12
-G(M-)-4 0 0 o O
37d Simplex 4ble,
B Xe , 3,S2 Su A
4 0 o -4o -/2
2nd Sumpkx teble, - O 0 M-
o 0 0 0 -Minsako,
C BXe S S, SaSy A/
3 o o 2
2 /4
Os, 5 o 3 'o5 -5 5/3
Since ol - i z
= 2 K, *
This &ub- þhoblem sheld be
branched Unko tw0 ub- bkoblems
0
Fos. = 0-S
2 o oo o-I
-Ci o -4 0 0 0 -
Poge-8

9. Seluken th áub- ptoblam (s)2 CStot aCHo
1st toble,
Max Z +Y2
S.T, 2 + 4x2 S+
5x, +3x, S IS
4 0 0 0 0 0 -
5
O 7 |2 4
Ss A
/2
5/5
O 0 0
Z 2
2 0 -M 2 o 0 o - o
Standord hotum: Z- (-M) 9 o o0 Mo O
2 oble,
Max Z : Xi t*2 0S,+0S,+0Sg+0S +05-MA
S.T
5o +3xt Sa =I5
O o o2 o-2 3/y
O
o IO 50 5|5/3
- Sy +A = 2
+ S 5 0
2
-g O- O O O - 0 M
Roge-9

10. 3d table, @hot pracko
0 0 0 0 0 -M Minralo
6Xe S, S2 S (5 Ss Ae|Sy
Sunu oll -g 20
a 3,%,=OO
oo o -35/5
o
0 0 0 0 I Selukon ot Sub-problem (6)
Max 7 = +H
S.T 2a +42 7
5x, +3X 'S
O0 0 0
h fable
2 2
Cp6Xe, , S Sa S S, Ss A
o S
Sy
2
Sub- problem.
hos mo heosible
Seluion
is dropbed
0 s
0 I -3/s Ihis
S
is ub- þroblem
Hence
Oo s 0 0-%.
I 0 0 0 0
O 00Ys 0 0 J
Poge-to

11. Among the
the best integer
aNoilable indeget-valued solukon,
Condilien/Soluiom is ven
@sHordt procko
Sub- þroblem (3).
Jhe otimsm deges
solukon is
=Iaond
Max Z=5
foge-

12. C5tatt pacti
Ornigtnal Problem
Max Z , +4Xa
S.T, 2 +41 +
5at 3x, |5
Solukion 0 ,
Sub- þroblem() Suh-ppobn(a
Max Z X +4a
5.T 2, +Hx1 S+
5x 3,S 15
Max Ze +1
S.T 2x +42 st
5a, +3, S1S
a22
Soluhiom:1, ar4.| Solukion : nbe Hon
2 2
| Suub-probLm (8)
|Max Z =it9*2
S.T 2,+4at
Sa+3 SIS
Sub-pro blem ()
Max Z *t4X2|
S.T, 2 +Y1
2 2
Soludiom: , =|| Seluukion:2, 3=
sol
1-5
Sub-problam.5)
Max 2- , +442
S.T, 24t4 t
5a, +3x I5
Sub-Probem (
Max : +92
S.T, 2, +YX, 7
5t3x T1S
72
.
72
aZ
ueen: i , 0 Seluken : No kesible
Soton