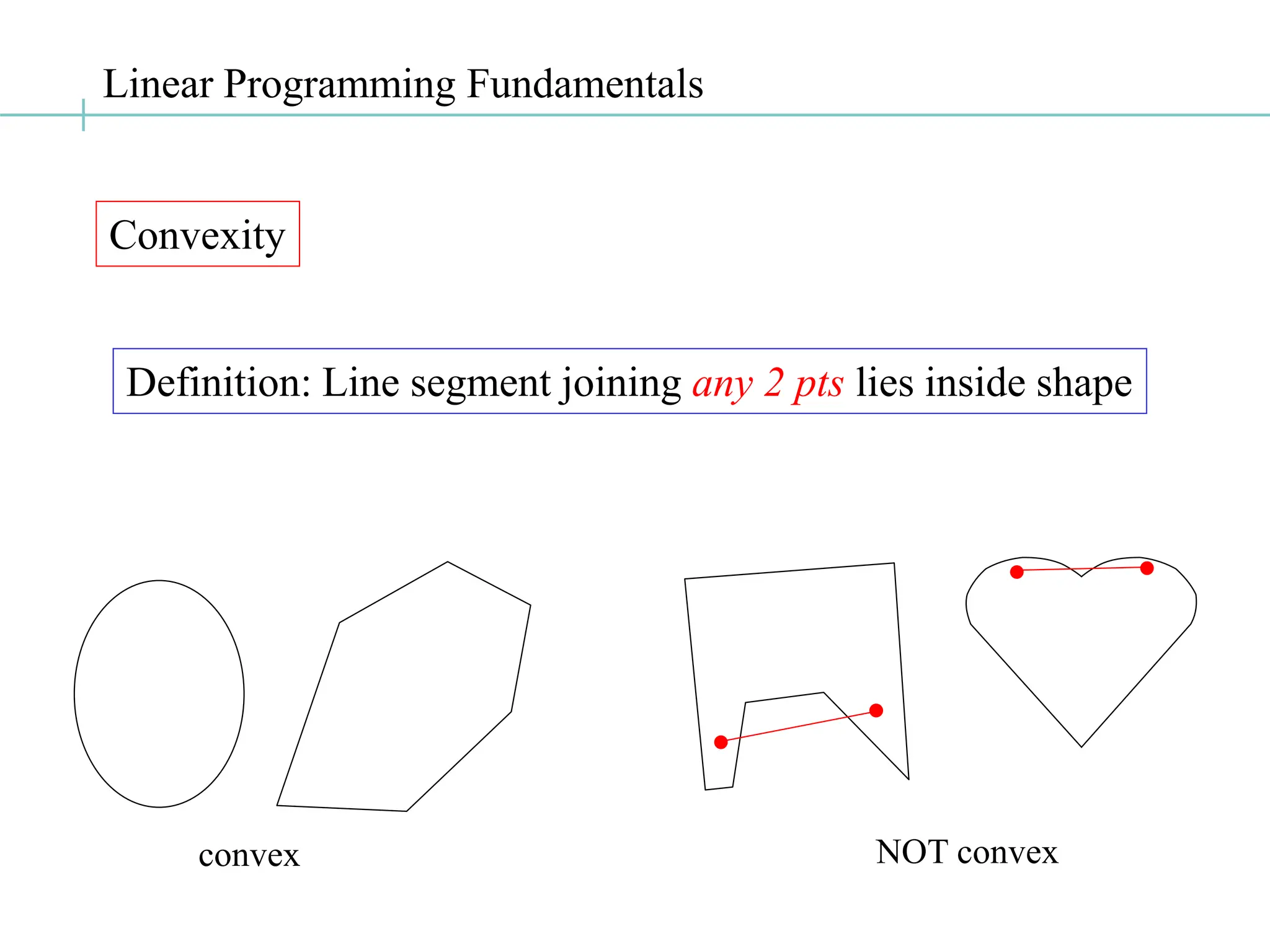
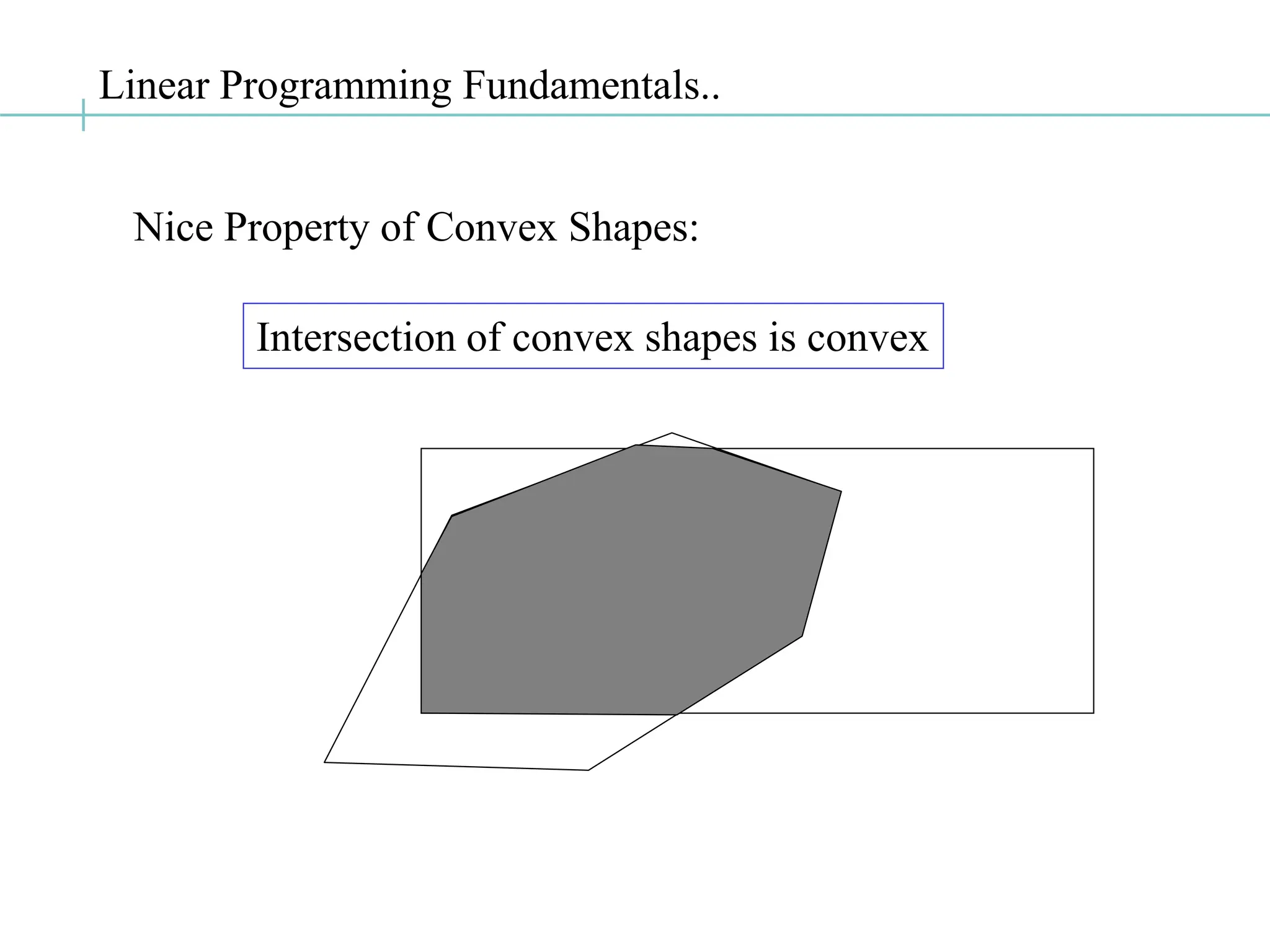
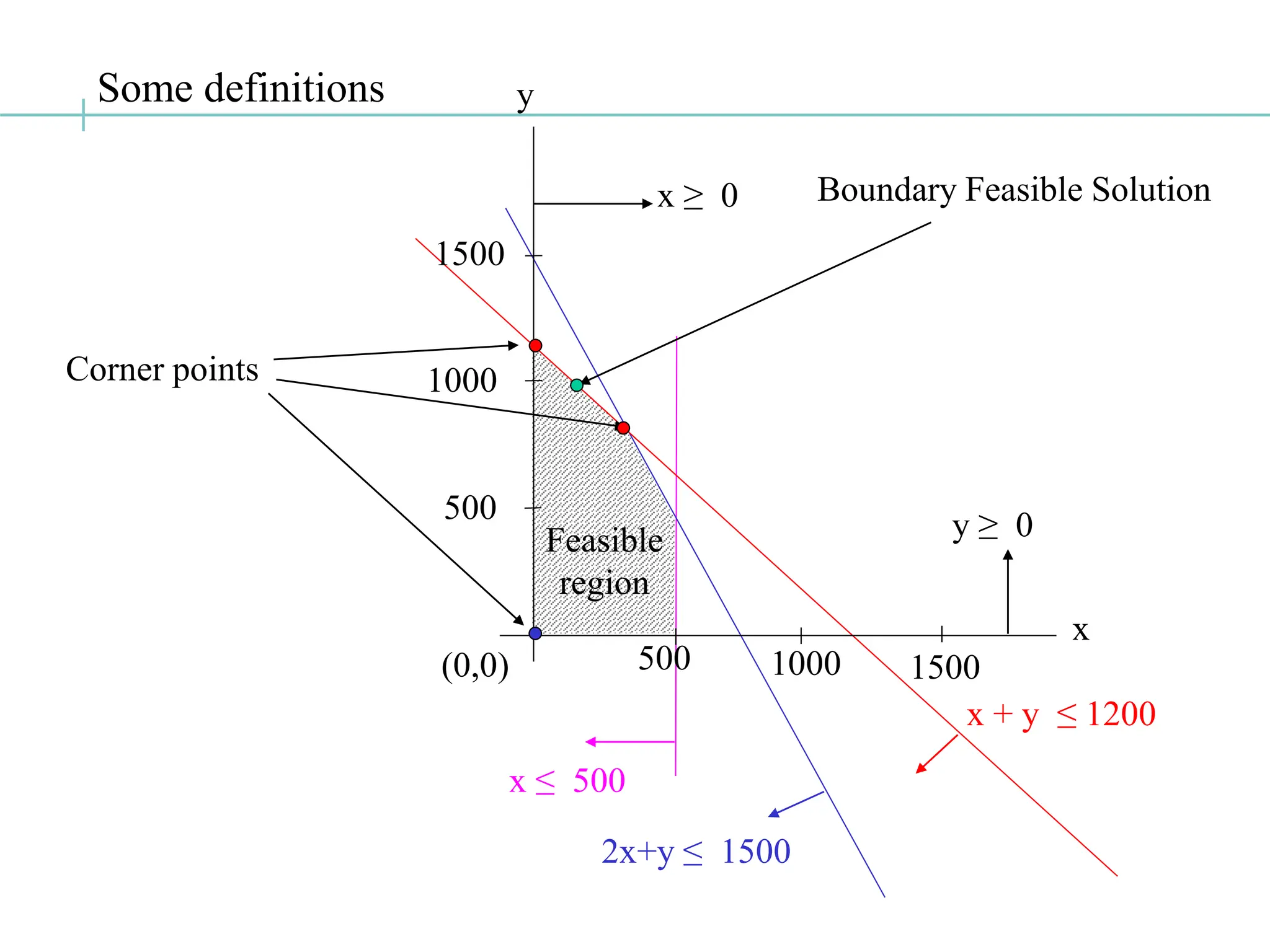
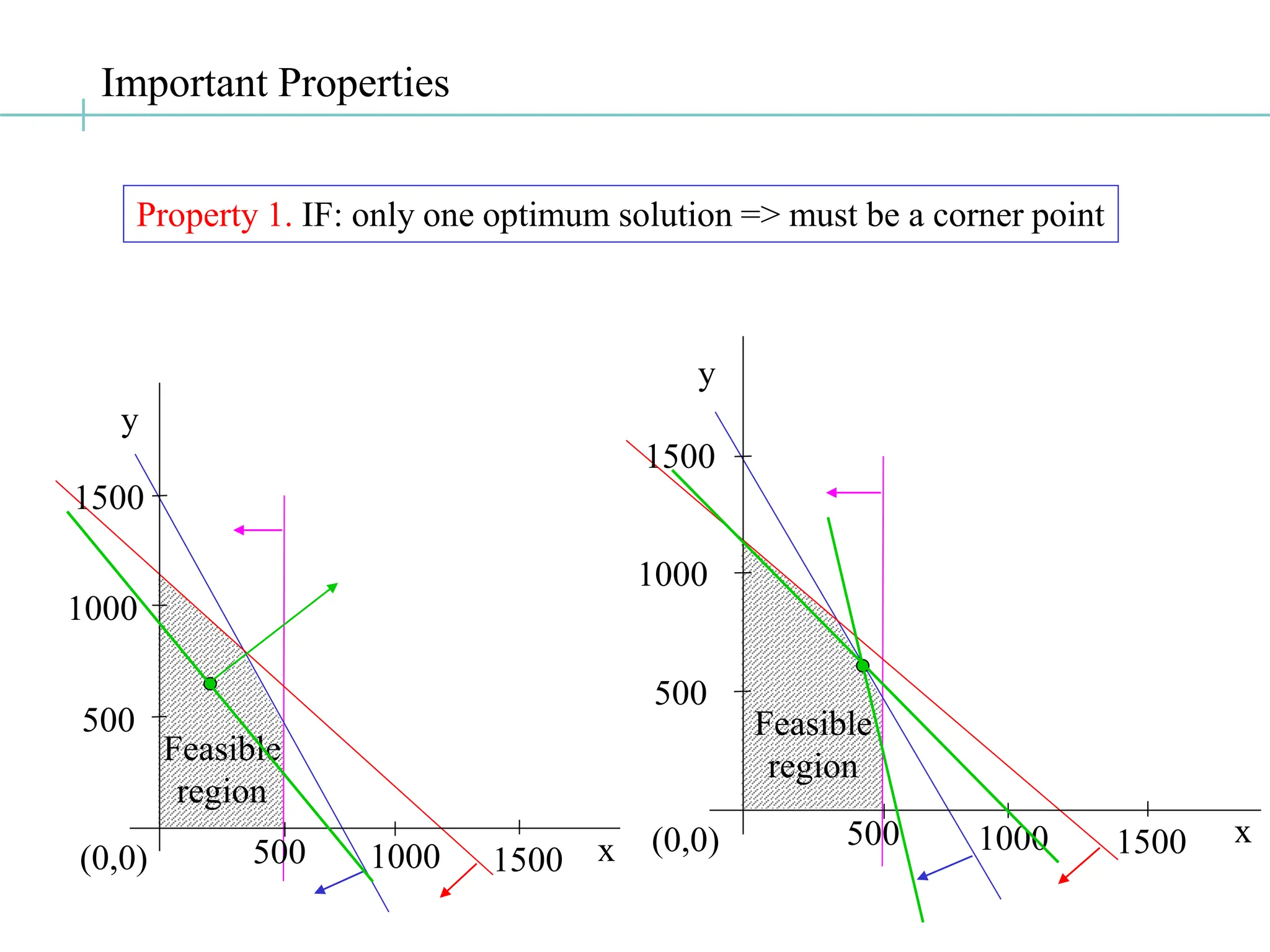
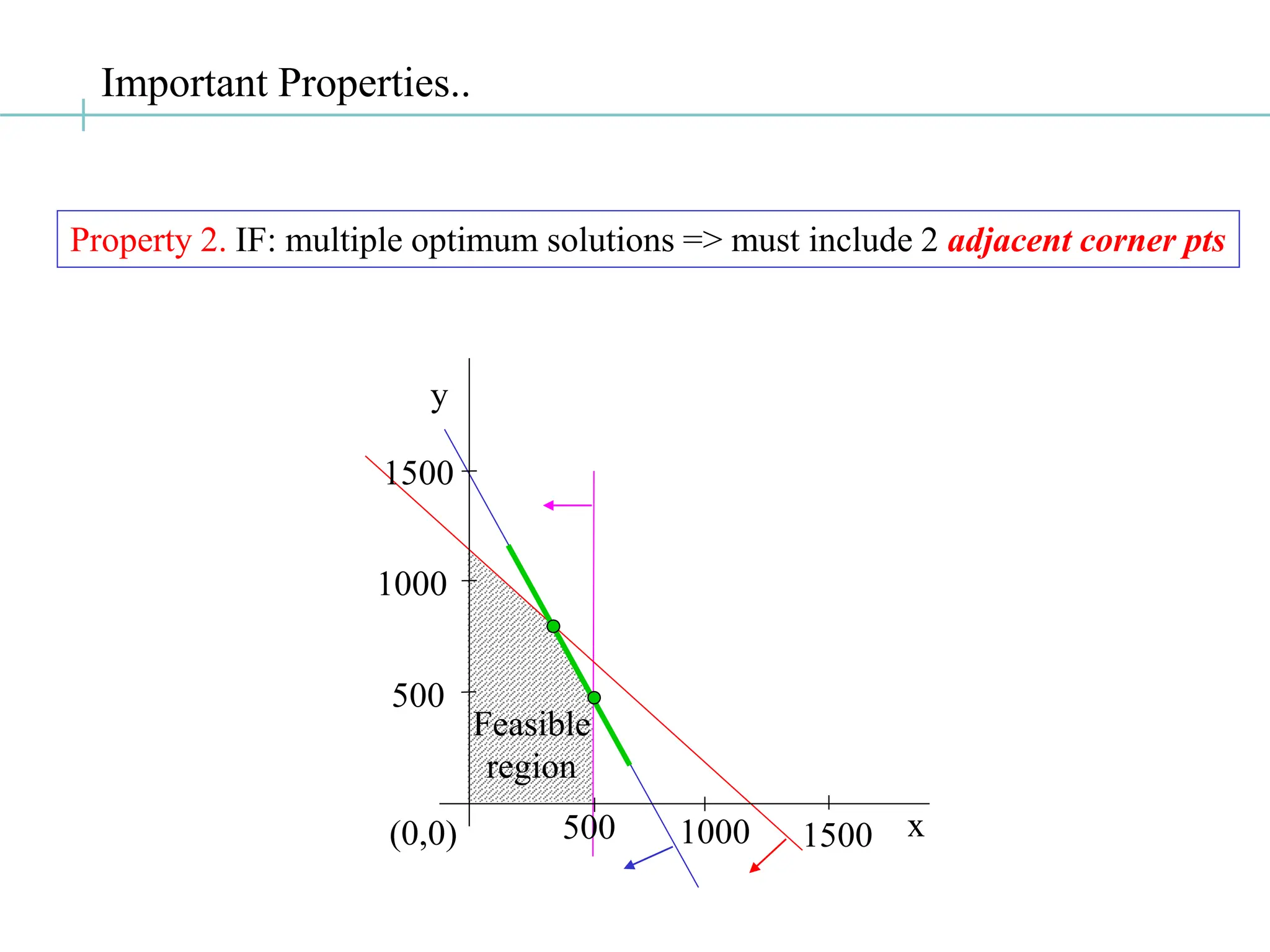
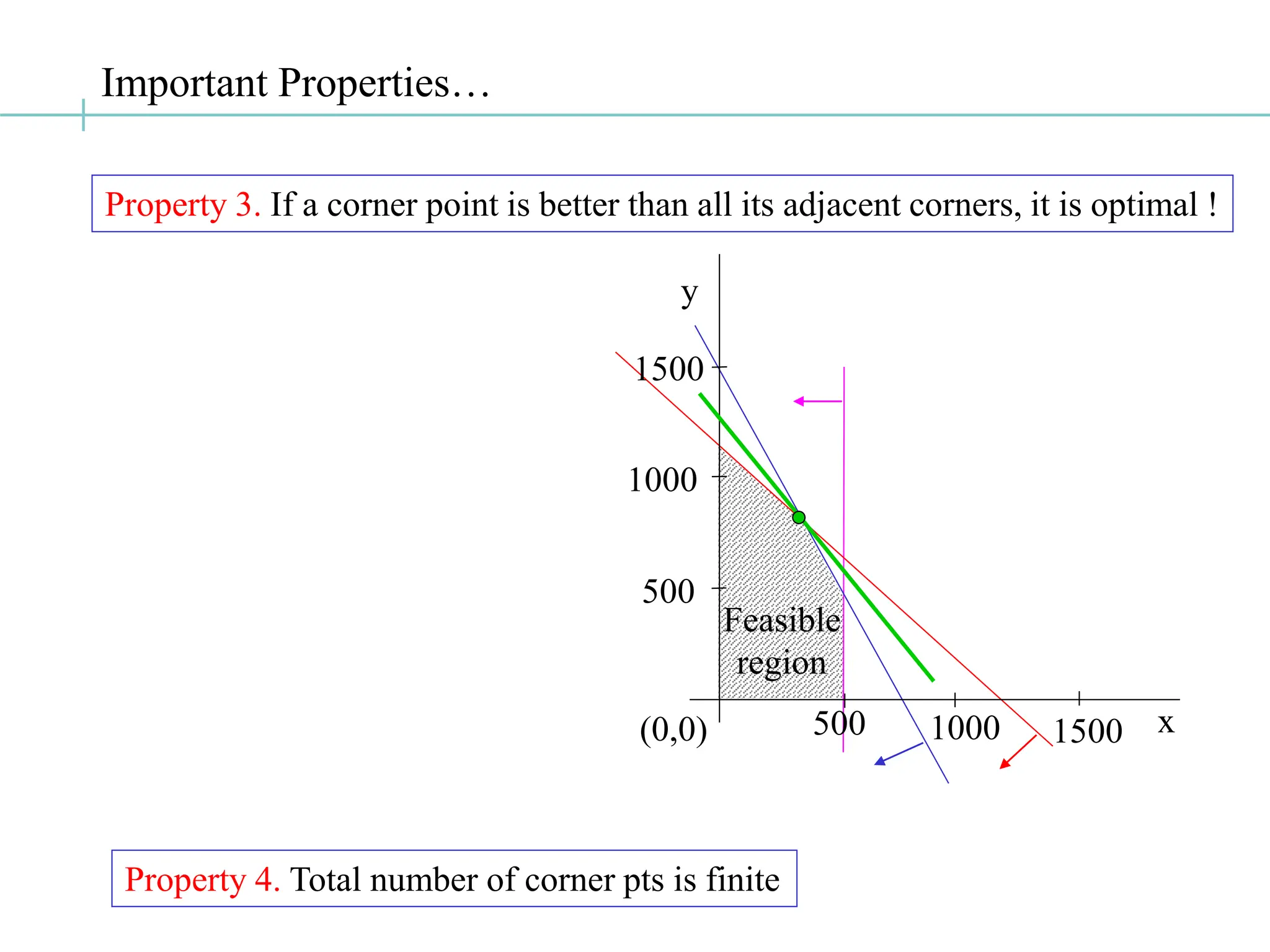
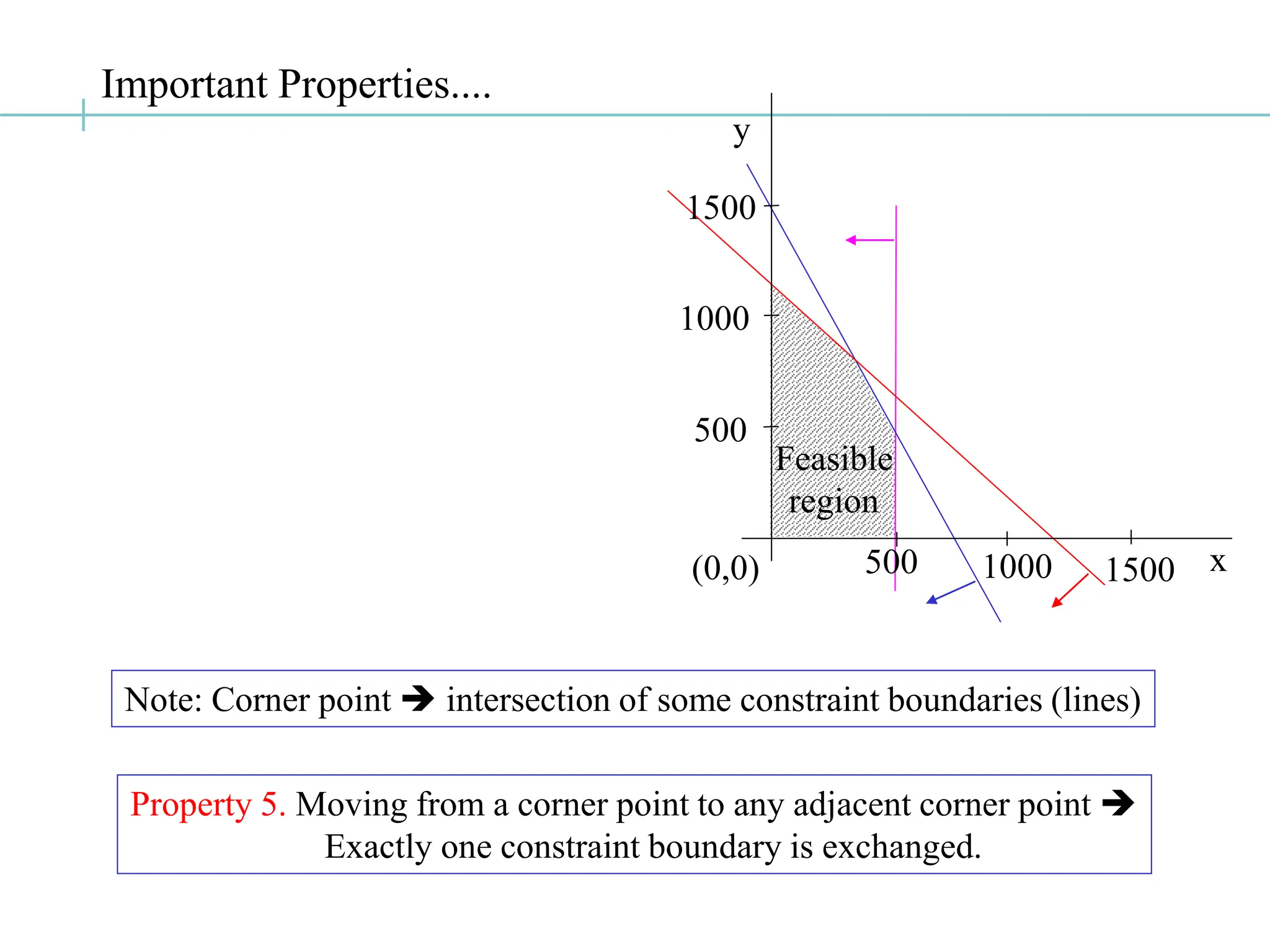
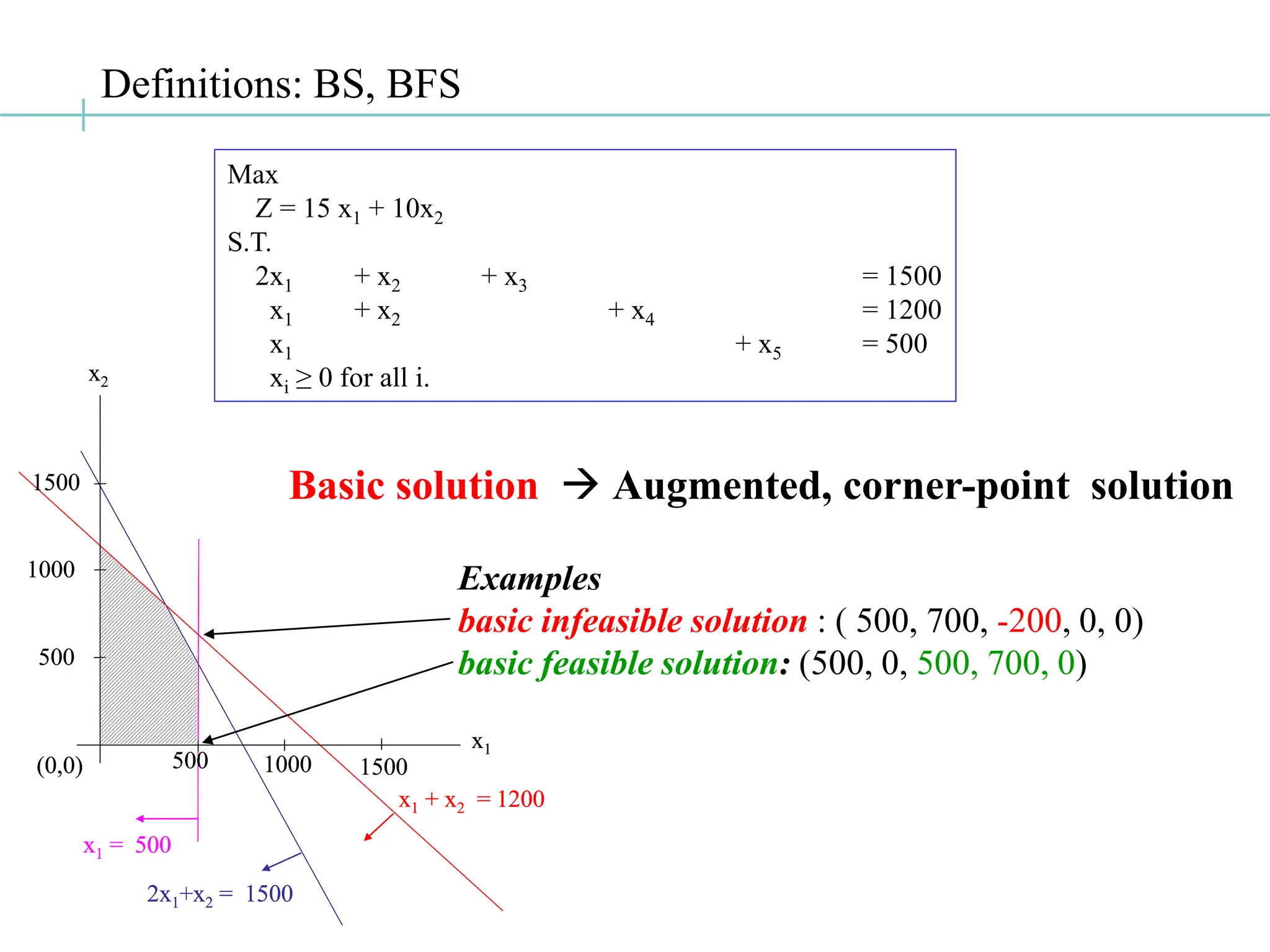
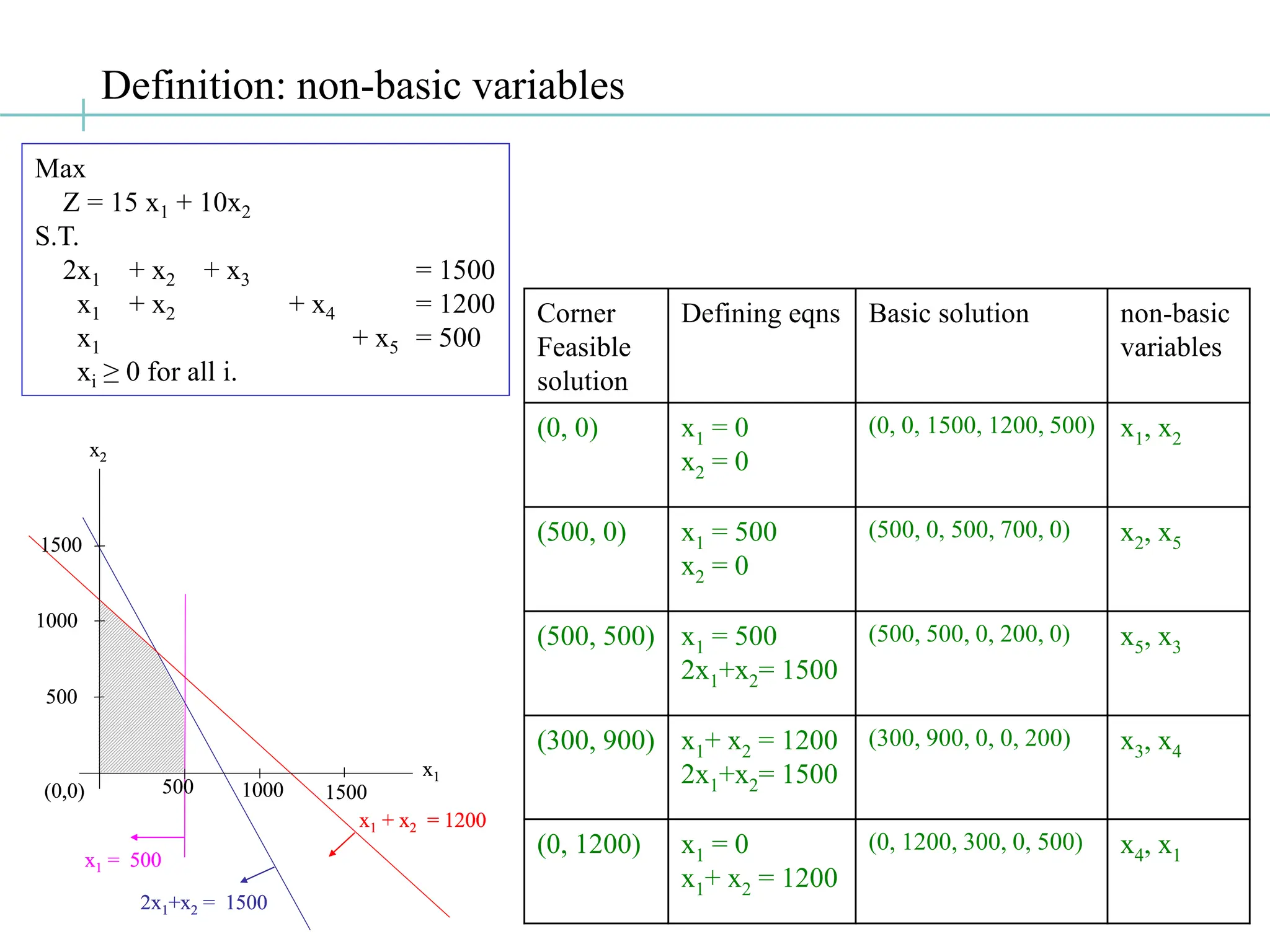
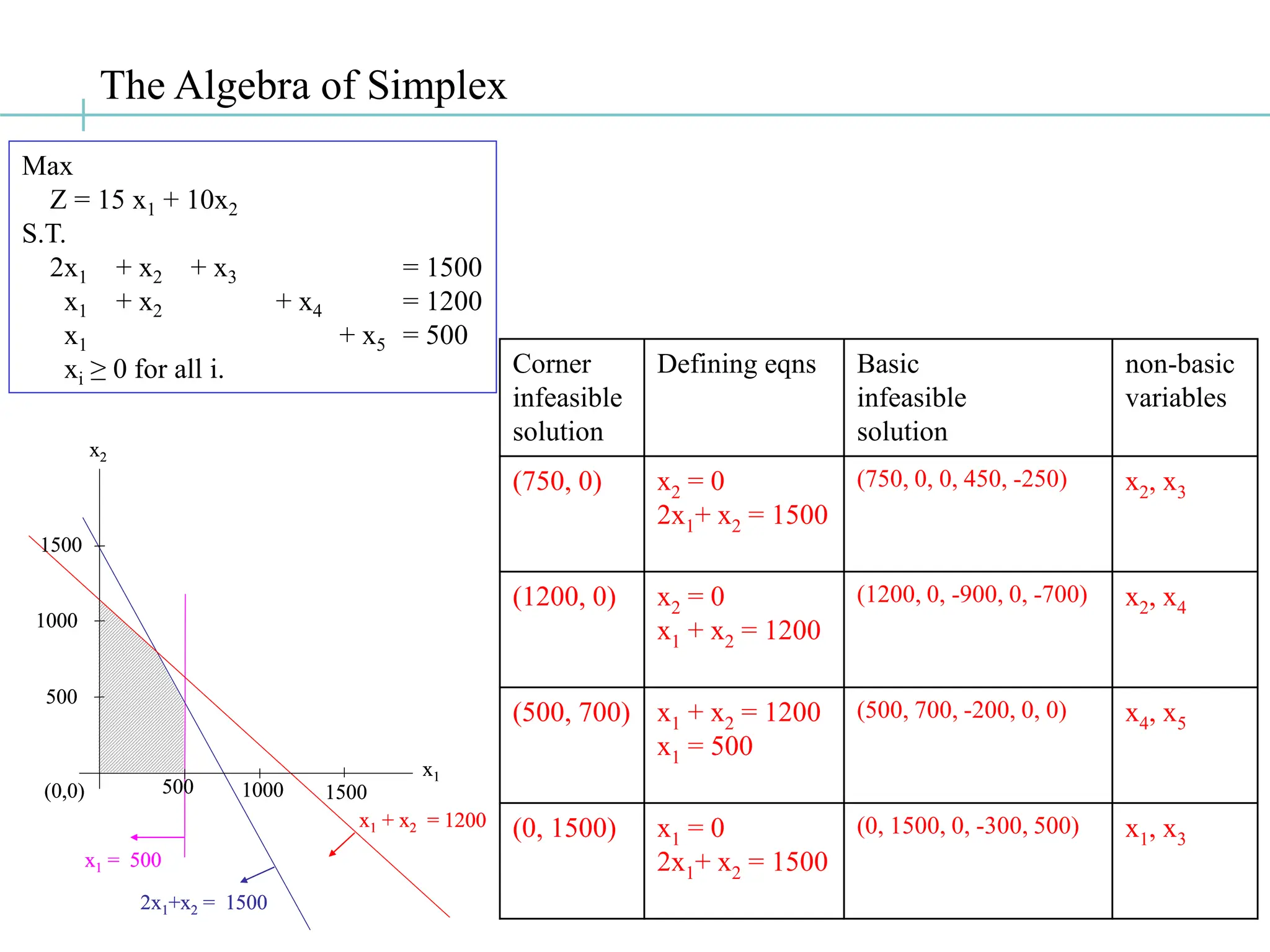
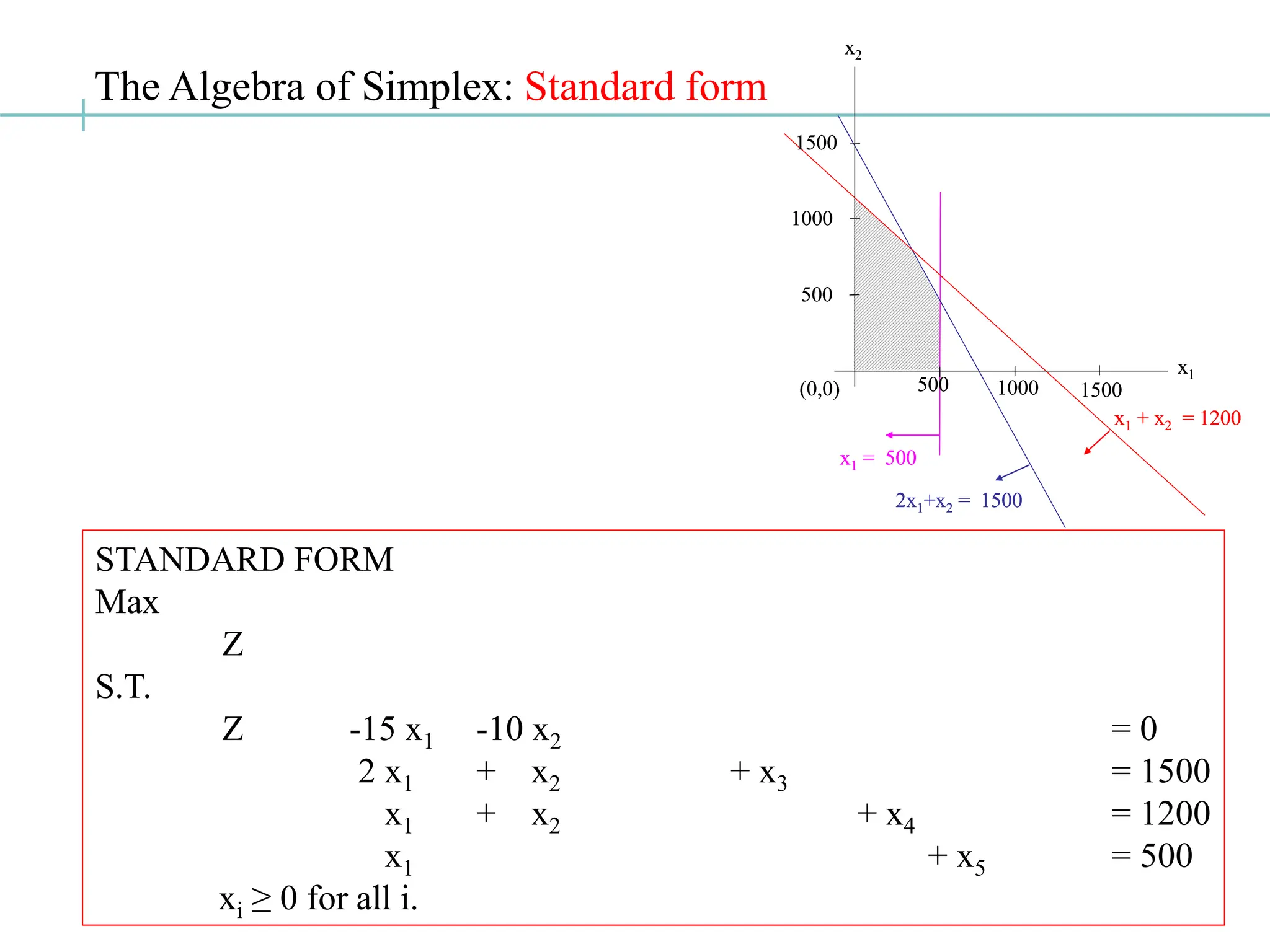
The document discusses the fundamentals of linear programming, focusing on the concept of convexity and the properties of feasible solutions represented as convex polyhedra. It outlines important characteristics of corner points, optimum solutions, and the simplex method for solving linear optimization problems, including an example conversion to standard form and the use of Gaussian elimination. The algebra of simplex is elaborated with steps on finding basic feasible solutions and iterations to optimize the objective function.

1. Linear Programming Fundamentals
Convexity
Definition: Line segment joining any 2 pts lies inside shape
convex NOT convex

2. Linear Programming Fundamentals..
Nice Property of Convex Shapes:
Intersection of convex shapes is convex

3. Linear Programming Fundamentals…
Every Half-space is convex
 Set of feasible solutions is a convex polyhedron
Each constraint of an LP  half space

4. Some definitions
y ≥ 0
x ≥ 0
x ≤ 500
2x+y ≤ 1500
x + y ≤ 1200
(0,0)
1000
1500
500 1000 1500
500
y
x
Feasible
region
Boundary Feasible Solution
Corner points

5. Important Properties
(0,0)
1000
1500
500 1000 1500
500
y
x
Feasible
region
Property 1. IF: only one optimum solution => must be a corner point
(0,0)
1000
1500
500 1000 1500
500
y
x
Feasible
region

6. Important Properties..
(0,0)
1000
1500
500 1000 1500
500
y
x
Feasible
region
Property 2. IF: multiple optimum solutions => must include 2 adjacent corner pts

7. Important Properties…
(0,0)
1000
1500
500 1000 1500
500
y
x
Feasible
region
Property 4. Total number of corner pts is finite
Property 3. If a corner point is better than all its adjacent corners, it is optimal !

8. Important Properties....
(0,0)
1000
1500
500 1000 1500
500
y
x
Feasible
region
Note: Corner point  intersection of some constraint boundaries (lines)
Property 5. Moving from a corner point to any adjacent corner point 
Exactly one constraint boundary is exchanged.

9. The algebra of Simplex
Good news
We only need to search for the best feasible corner point
Good news
We can use property 5 to guide our searching
Bad news
A problem with 50 variables, 100 constraints =>
100 !
50 ! (100-50) !
=> ~ 1029 corner points

10. The outline of Simplex
1. Start at a corner point feasible solution
2. If (there is a better adjacent corner feasible point) then
go to one such adjacent corner point;
repeat Step 2;
else (report this point as the optimum point).
Why does this method work ?
1. Constant improvement (=> no cycling)
2. Finite number of corners

11. The Algebra of Simplex: Gauss elimination
Solving for corner points   solving a set of simultaneous equations
Method: Gaussian elimination
Example:
x + y = 2 [1]
x – 2y = 1 [2]
Solve by:
2x[1] + [2]: 3x = 5 => x = 5/3
[1] - 1x[2]: 3y = 1 => y = 1/3

12. The Algebra of Simplex: need for Slack !
Cannot add (multiples of) INEQUATIONS !!
Consider:
x >= 0 [1]
y >= 0 [2]
[1] + [2]: x + y >= 0 [3]
x
y
x + y >= 0

13. The Algebra of Simplex: Slack
To allow us to use Gaussian elimination,
Convert the inequalities to equations by using SLACK Variables
2x + y ≤ 1500,
x, y ≥ 0
2x + y + s = 1500,
x, y, s ≥ 0
x + y ≥ 200
x, y ≥ 0
x + y – s = 200,
x, y, s ≥ 0.
Inequality Equality, with slack variable

14. The Algebra of Simplex..
Conversion of the Product mix problem
ORIGINAL
Maximize
z( x, y) = 15 x + 10y
subject to
2x + y ≤ 1500
x + y ≤ 1200
x ≤ 500
x ≥ 0,
y ≥ 0
(almost) STANDARD FORM
Maximize
Z = 15 x1 + 10x2
subject to
2x1 + x2 + x3 = 1500
x1 + x2 + x4 = 1200
x1 + x5 = 500
xi ≥ 0 for all i.

15. ORIGINAL
Maximize
z( x, y) = 15 x + 10y
subject to
2x + y ≤ 1500
x + y ≤ 1200
x ≤ 500
x ≥ 0,
y ≥ 0
(almost) STANDARD FORM
Maximize
Z = 15 x1 + 10x2
subject to
2x1 + x2 + x3 = 1500
x1 + x2 + x4 = 1200
x1 + x5 = 500
xi ≥ 0 for all i.
Original problem: n variables, m constraints
Standard form: (m+n) variables, m constraints
The Algebra of Simplex…

16. Original problem: n variables, m constraints
Standard form: (m+n) variables, m constraints
How to use Gaussian elimination ??
Force some variables = 0
How many to be forced to be 0 ?
The Algebra of Simplex…

17. Definitions: augmented solution
x1 = 500
2x1+x2 = 1500
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
x1 = 500
x1 = 500
2x1+x2 = 1500
2x1+x2 = 1500
x1 + x2 = 1200
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
Solution: Augmented solution
(x1 x2) = (200, 200) (200, 200, 900, 800, 300)
Max
Z = 15 x1 + 10x2
S.T.
2x1 + x2 + x3 = 1500
x1 + x2 + x4 = 1200
x1 + x5 = 500
xi ≥ 0 for all i.

18. Definitions: BS, BFS
x1 = 500
2x1+x2 = 1500
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
x1 = 500
x1 = 500
2x1+x2 = 1500
2x1+x2 = 1500
x1 + x2 = 1200
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
Basic solution  Augmented, corner-point solution
Max
Z = 15 x1 + 10x2
S.T.
2x1 + x2 + x3 = 1500
x1 + x2 + x4 = 1200
x1 + x5 = 500
xi ≥ 0 for all i.
Examples
basic infeasible solution : ( 500, 700, -200, 0, 0)
basic feasible solution: (500, 0, 500, 700, 0)

19. Definition: non-basic variables
x1 = 500
2x1+x2 = 1500
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
x1 = 500
x1 = 500
2x1+x2 = 1500
2x1+x2 = 1500
x1 + x2 = 1200
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
Max
Z = 15 x1 + 10x2
S.T.
2x1 + x2 + x3 = 1500
x1 + x2 + x4 = 1200
x1 + x5 = 500
xi ≥ 0 for all i.
Corner
Feasible
solution
Defining eqns Basic solution non-basic
variables
(0, 0) x1 = 0
x2 = 0
(0, 0, 1500, 1200, 500) x1, x2
(500, 0) x1 = 500
x2 = 0
(500, 0, 500, 700, 0) x2, x5
(500, 500) x1 = 500
2x1+x2= 1500
(500, 500, 0, 200, 0) x5, x3
(300, 900) x1+ x2 = 1200
2x1+x2= 1500
(300, 900, 0, 0, 200) x3, x4
(0, 1200) x1 = 0
x1+ x2 = 1200
(0, 1200, 300, 0, 500) x4, x1

20. The Algebra of Simplex
x1 = 500
2x1+x2 = 1500
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
x1 = 500
x1 = 500
2x1+x2 = 1500
2x1+x2 = 1500
x1 + x2 = 1200
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
Max
Z = 15 x1 + 10x2
S.T.
2x1 + x2 + x3 = 1500
x1 + x2 + x4 = 1200
x1 + x5 = 500
xi ≥ 0 for all i. Corner
infeasible
solution
Defining eqns Basic
infeasible
solution
non-basic
variables
(750, 0) x2 = 0
2x1+ x2 = 1500
(750, 0, 0, 450, -250) x2, x3
(1200, 0) x2 = 0
x1 + x2 = 1200
(1200, 0, -900, 0, -700) x2, x4
(500, 700) x1 + x2 = 1200
x1 = 500
(500, 700, -200, 0, 0) x4, x5
(0, 1500) x1 = 0
2x1+ x2 = 1500
(0, 1500, 0, -300, 500) x1, x3

21. The Algebra of Simplex: Standard form
x1 = 500
2x1+x2 = 1500
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
x1 = 500
x1 = 500
2x1+x2 = 1500
2x1+x2 = 1500
x1 + x2 = 1200
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
STANDARD FORM
Max
Z
S.T.
Z -15 x1 -10 x2 = 0
2 x1 + x2 + x3 = 1500
x1 + x2 + x4 = 1200
x1 + x5 = 500
xi ≥ 0 for all i.

22. The Algebra of Simplex: Step 1. Initial solution
x1 = 500
2x1+x2 = 1500
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
x1 = 500
x1 = 500
2x1+x2 = 1500
2x1+x2 = 1500
x1 + x2 = 1200
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
Max
Z
S.T.
Z -15 x1 -10 x2 = 0
2 x1 + x2 + x3 = 1500
x1 + x2 + x4 = 1200
x1 + x5 = 500
xi ≥ 0 for all i.
( 0, 0)
Initial non-basic variables: (x1, x2)
Initial basic variables: (x3, x4 , x5)
Initial BFS: (0, 0, 1500, 1200, 500)

23. The Algebra of Simplex: Step 2. Iteration Step
x1 = 500
2x1+x2 = 1500
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
x1 = 500
x1 = 500
2x1+x2 = 1500
2x1+x2 = 1500
x1 + x2 = 1200
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
Entering variable:
Z = 15 x1 + 10x2
Fastest rate of ascent

24. The Algebra of Simplex: Step 2. Iteration Step
Leaving variable
Max Z
S.T.
Z -15 x1 - 10x2 = 0
2x1 + x2 + x3 = 1500
x1 + x2 + x4 = 1200
x1 + x5 = 500
xi ≥ 0 for all i.
Consider first constraint:
Entering
2x1 + x2 + x3 = 1500
x3 = 1500 - 2x1 - x2
Bound on x1: 1500/2 = 750

25. The Algebra of Simplex: Step 2. Iteration Step
Basic
variable
Equation Upper bound for x1
x3 x3 = 1500 - 2x1 - x2 x2 = 0, so x1 ≤ 1500/2; UB = 750
x4 x4 = 1200 - x1 - x2 x2 = 0, so x1 ≤ 1200; UB = 1200
x5 x5 = 500 - x1 x1 ≤ 500  minimum
Max Z
S.T.
Z -15 x1 - 10x2 = 0
2x1 + x2 + x3 = 1500
x1 + x2 + x4 = 1200
x1 + x5 = 500
xi ≥ 0 for all i.
Leaving variable

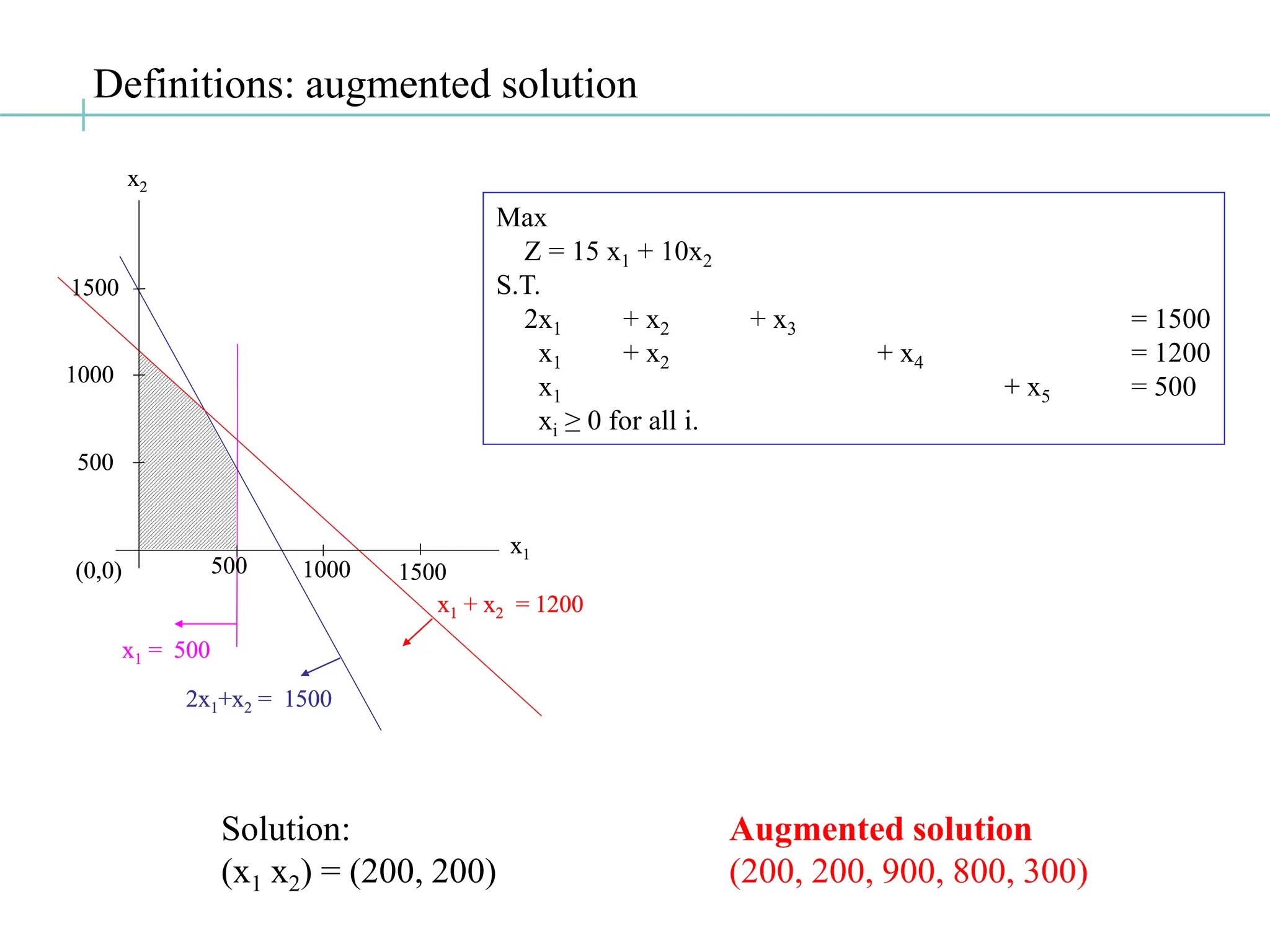
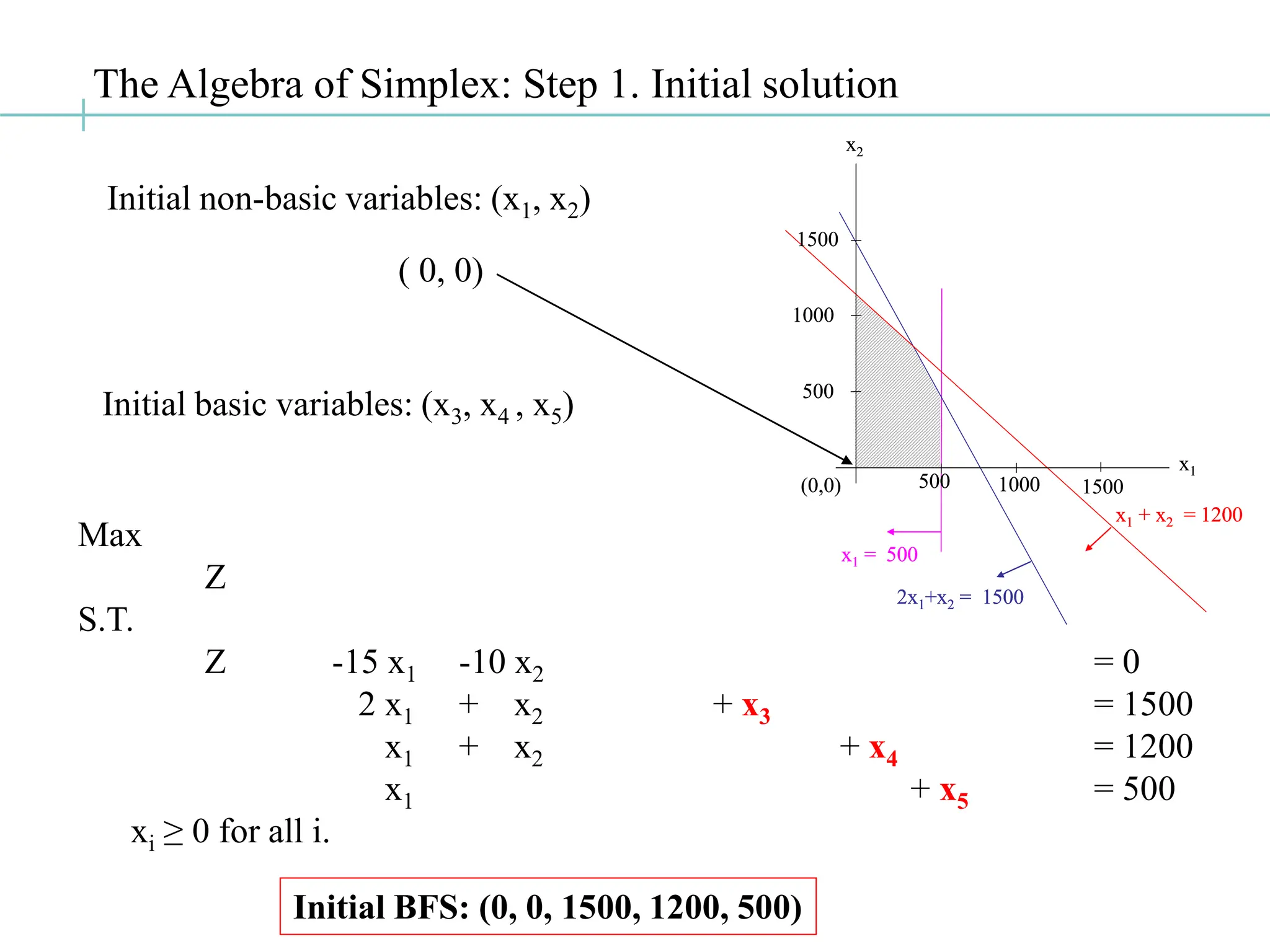
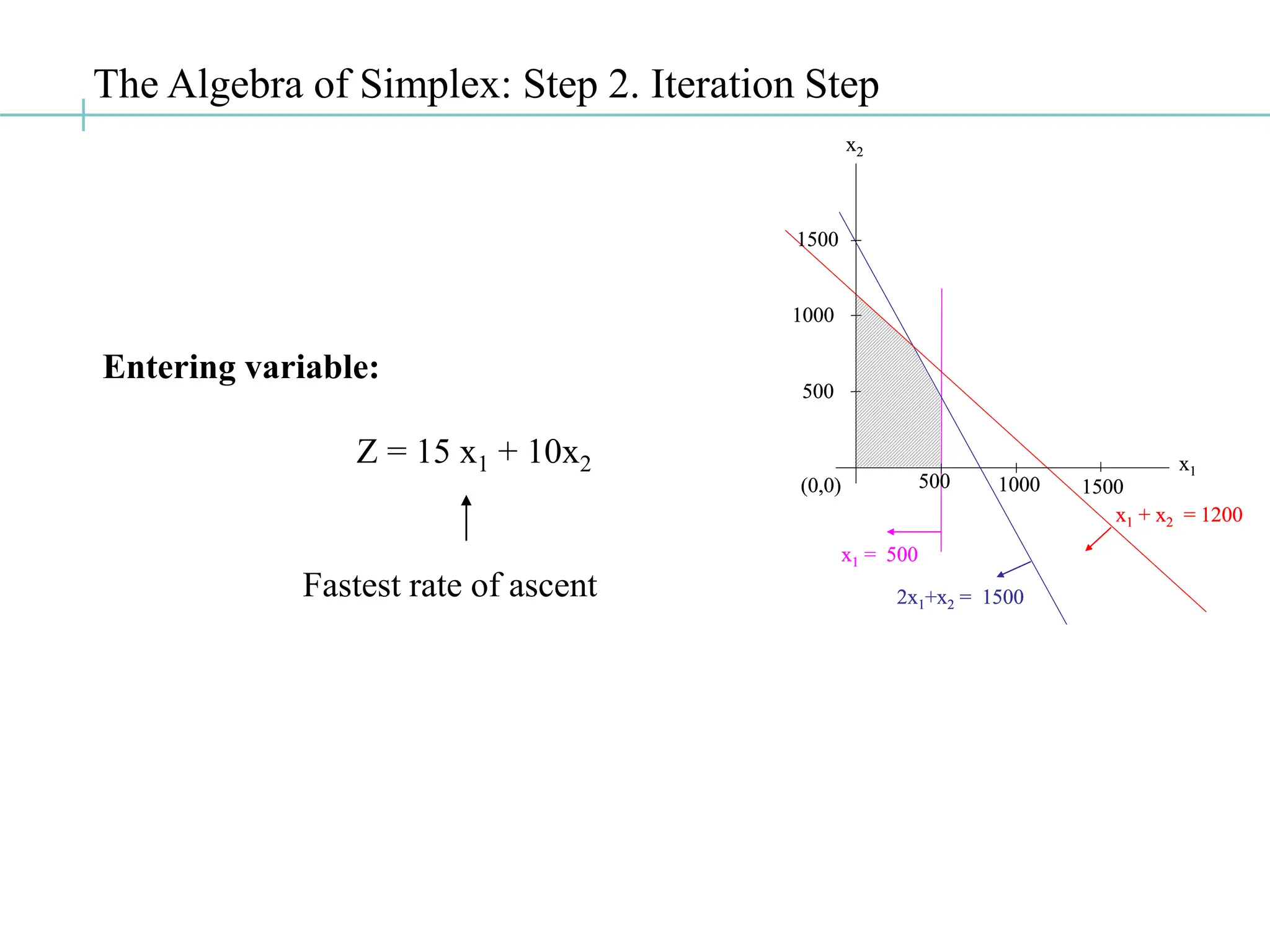
26. The Algebra of Simplex: Step 2. Iteration Step
Enter: x1 Leave: x5
Z -15 x1 -10x2 = 0 [0-0]
2 x1 + x2 + x3 = 1500 [0-1]
x1 + x2 + x4 = 1200 [0-2]
x1 + x5 = 500 [0-3]
ROW OPERATIONS so that
Each row has exactly one basic variable
The coefficient of each basic variable = +1
- [0-3]
- 2x [0-3]
+ 15x [0-3]

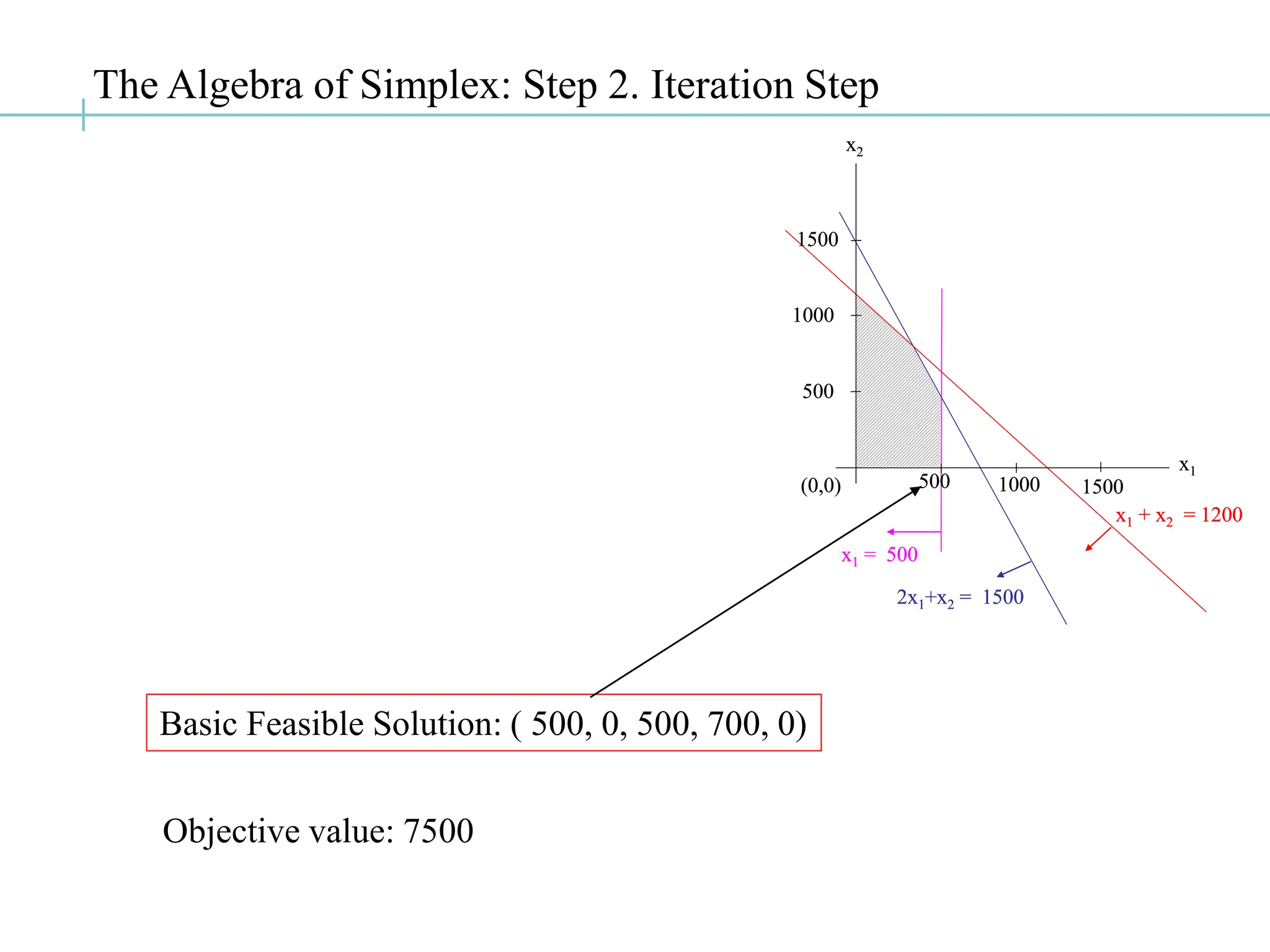
27. The Algebra of Simplex: Step 2. Iteration Step
Z -15 x1 -10x2 = 0 [0-0]
2 x1 + x2 + x3 = 1500 [0-1]
x1 + x2 + x4 = 1200 [0-2]
x1 + x5 = 500 [0-3]
Z -10x2 +15 x5 = 7500 [1-0]
x2 + x3 - 2 x5 = 500 [1-1]
x2 + x4 - x5 = 700 [1-2]
x1 + x5 = 500 [1-3]
Row operations
Basic Feasible Solution: ( 500, 0, 500, 700, 0)

28. The Algebra of Simplex: Step 2. Iteration Step
x1 = 500
2x1+x2 = 1500
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
x1 = 500
x1 = 500
2x1+x2 = 1500
2x1+x2 = 1500
x1 + x2 = 1200
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
Basic Feasible Solution: ( 500, 0, 500, 700, 0)
Objective value: 7500

29. The Algebra of Simplex: Step 3. Stopping condition
Z -10x2 +15 x5 = 7500 [1-0]
x2 + x3 - 2 x5 = 500 [1-1]
x2 + x4 - x5 = 700 [1-2]
x1 + x5 = 500 [1-3]
Stopping Rule: Stop when objective cannot be improved.
New entering variable: x2

30. The Algebra of Simplex: Second Iteration..
Z -10x2 +15 x5 = 7500 [1-0]
x2 + x3 - 2x5 = 500 [1-1]
x2 + x4 - x5 = 700 [1-2]
x1 + x5 = 500 [1-3]
New entering variable: x2
Basic
variable
Equation Upper bound for x2
x3 x3 = 500 – x2 + 2x5 x2 ≤ 500  minimum
x4 x4 = 700 – x2 + x5 x2 ≤ 700
x1 x1 = 500 – x5 no limit on x2
Analysis for leaving variable:

31. The Algebra of Simplex: Step 2. Iteration Step
Enter: x2 Leave: x3
ROW OPERATIONS so that
Each row has exactly one basic variable
The coefficient of each basic variable = +1
- [1-1]
+ 10x [1-1]
Z -10x2 +15 x5 = 7500 [1-0]
x2 + x3 - 2x5 = 500 [1-1]
x2 + x4 - x5 = 700 [1-2]
x1 + x5 = 500 [1-3]

32. The Algebra of Simplex: Step 2. Iteration Step
Basic Feasible Solution:
After row operations:
Z +10 x3 -5 x5 = 12,500 [2-0]
x2 + x3 - 2x5 = 500 [2-1]
- x3 + x4 + x5 = 200 [2-2]
x1 + x5 = 500 [2-3]
x1 = 500
2x1+x2 = 1500
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
x1 = 500
x1 = 500
2x1+x2 = 1500
2x1+x2 = 1500
x1 + x2 = 1200
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
( 500, 500, 0, 200, 0)
Have we found the OPTIMUM ?

33. The Algebra of Simplex: Third Iteration
New entering variable: x5
Analysis for leaving variable:
Z +10 x3 -5 x5 = 12,500 [2-0]
x2 + x3 - 2x5 = 500 [2-1]
- x3 + x4 + x5 = 200 [2-2]
x1 + x5 = 500 [2-3]
Basic
variable
Equation Upper bound for x5
x2 x2 = 500 + 2x5 - x3 no limit on x5
x4 x4 = 200 + x3 - x5 x5 ≤ 200  minimum
x1 x1 = 500 – x5 x5 ≤ 500

34. The Algebra of Simplex: Step 2. Third iteration..
ROW OPERATIONS so that
Each row has exactly one basic variable
The coefficient of each basic variable = +1
- [2-2]
+ 5x [2-2]
Enter: x5 Leave: x4
Z +10 x3 -5 x5 = 12,500 [2-0]
x2 + x3 - 2x5 = 500 [2-1]
- x3 + x4 + x5 = 200 [2-2]
x1 + x5 = 500 [2-3]
+ 2x [2-2]

35. The Algebra of Simplex: Step 2. Iteration Step
Basic Feasible Solution:
x1 = 500
2x1+x2 = 1500
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
x1 = 500
x1 = 500
2x1+x2 = 1500
2x1+x2 = 1500
x1 + x2 = 1200
x1 + x2 = 1200
(0,0)
1000
1500
500 1000 1500
500
x2
x1
( 300, 900, 0, 0, 200)
Have we found the OPTIMUM ?
After row operations:
Z +5 x3 + 5x4 = 13,500 [3-0]
x2 - x3 + 2x4 = 900 [3-1]
- x3 + x4 + x5 = 200 [3-2]
x1 + x3 - x4 = 300 [3-3]

36. The Algebra of Simplex: Some important points
1. Higher dimensions
2. Many candidates for entering variable
Each step:
ONE entering variable
ONE leaving variable
 Each constraint equation has
has same format as our example
e.g. Z = 200 + 10x1 + x2 + 10x3
Just pick any one

37. The Algebra of Simplex: Some important points..
3. Many candidates for leaving variable
4. No candidate for leaving variable
5. Minimization problems
Degenerate case, rare.
Unbounded objective !?
Minimize Z == Maximize -Z
next topic: inventory control