The document contains 8 solved problems related to linear programming and network flows:
1. Uses the simplex method to solve a linear programming problem to maximize an objective function subject to constraints.
2. Again uses the simplex method to solve another linear programming problem with an objective function and constraints.
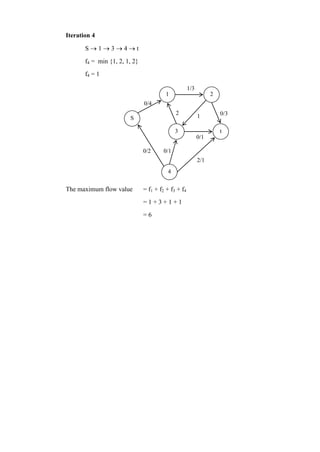
3. Solves a transportation problem through iterative steps to find the maximum flow between sources and targets.
4. Finds the maximum flow in a network using multiple paths and iterations.
5. Finds the maximum matching in a bipartite graph through unique pairings.
6. Finds the maximum matching for another matching problem instance.
7. Finds a good matching for a marriage problem by considering men's and women's