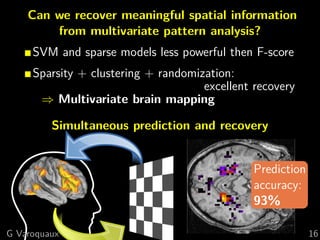
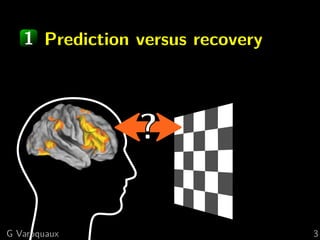
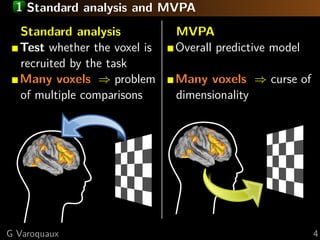
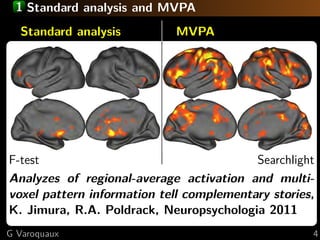
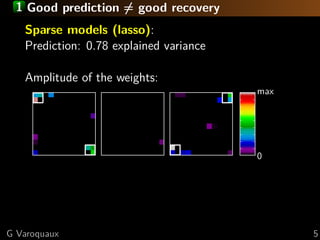
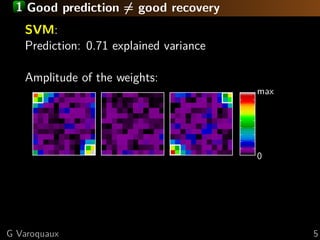
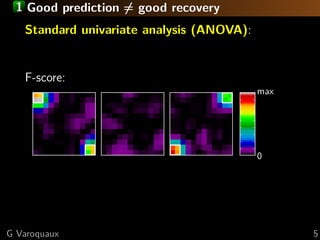
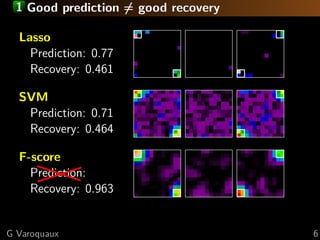
The document discusses the potential of recovering meaningful spatial information using multivariate pattern analysis (MVPA) techniques in fMRI studies. It compares various methods, including sparse models and standard univariate analysis, to highlight the effectiveness of combining clustering and randomization for feature recovery. The findings suggest that with appropriate modeling, high prediction accuracy can be achieved in brain mapping tasks.

1. Can we recover meaningful spatial informa-
tion from multivariate pattern analysis?
Ga¨l Varoquaux
e INRIA/Parietal
Alexandre
Gramfort
Bertrand
Thirion

2. Can we recover meaningful spatial informa-
tion from multivariate pattern analysis?
Ga¨l Varoquaux
e INRIA/Parietal
Alexandre
Gramfort
Bertrand
Thirion
Yes we can!

3. Can we recover meaningful spatial informa-
tion from multivariate pattern analysis?
Ga¨l Varoquaux
e INRIA/Parietal
Alexandre
Gramfort
Bertrand
Thirion

4. 1 Prediction versus recovery
2 Random parcellations and sparsity
G Varoquaux 2

5. 1 Prediction versus recovery
?
G Varoquaux 3

6. 1 Standard analysis and MVPA
Standard analysis MVPA
Test whether the voxel is Overall predictive model
recruited by the task
Many voxels ⇒ problem Many voxels ⇒ curse of
of multiple comparisons dimensionality
G Varoquaux 4

7. 1 Standard analysis and MVPA
Standard analysis MVPA
Test whether the voxel is Overall predictive model
recruited by the task
Many voxels ⇒ problem Many voxels ⇒ curse of
of multiple comparisons dimensionality
F-test Searchlight
Analyzes of regional-average activation and multi-
voxel pattern information tell complementary stories,
K. Jimura, R.A. Poldrack, Neuropsychologia 2011
G Varoquaux 4

8. 1 Good prediction = good recovery
Simple simulations: y = w X + e
X: observed fMRI images: spatially smooth
e: noise
w: coefficients (brain regions)
Ground truth
G Varoquaux 5

9. 1 Good prediction = good recovery
Sparse models (lasso):
Prediction: 0.78 explained variance
Amplitude of the weights:
max
0
G Varoquaux 5

10. 1 Good prediction = good recovery
SVM:
Prediction: 0.71 explained variance
Amplitude of the weights:
max
0
G Varoquaux 5

11. 1 Good prediction = good recovery
Standard univariate analysis (ANOVA):
F-score:
max
0
G Varoquaux 5

12. 1 Good prediction = good recovery
Lasso
Prediction: 0.77
Recovery: 0.461
SVM
Prediction: 0.71
Recovery: 0.464
F-score
Prediction:
Recovery: 0.963
G Varoquaux 6

13. 1 Multivariate analysis for recovery?
Considering each voxel separately is
suboptimal: they share information
Most often, we know that we are looking for
a small fraction of the cortex
A voxel is more likely to be activated
if its neighbor is
G Varoquaux 7

14. 1 Multivariate analysis for recovery?
Considering each voxel separately is
suboptimal: they share information
Most often, we know that we are looking for
a small fraction of the cortex
Sparse models
A voxel is more likely to be activated
if its neighbor is
Spatial models
G Varoquaux 7

15. 1 Sparse models
Compressive sensing:
detection of k signals out of p (voxels)
with only n observations ∝ k
Iterpretable
Selects random subsets in correlated signals
Face vs house
discrimination
Data from [Haxby 2001]
G Varoquaux 8

16. 1 Sparse models
Compressive sensing:
detection of k signals out of p (voxels)
with only n observations ∝ k
Iterpretable
Selects random subsets in correlated signals
Stability selection:
Face vsrandom perturbations to the data
Apply house
discrimination that are selected often
Keep voxels
Data from [Haxby 2001] [Meinhausen 2010]
G Varoquaux 8

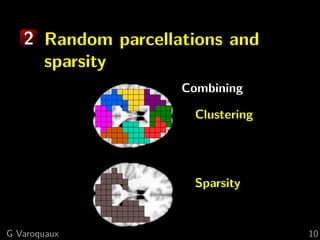
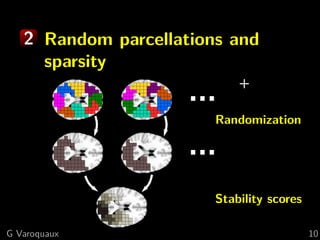
17. 1 Spatial models
Brain parcellations:
Ward clustering to reduce voxel numbers
Supervised clustering [Michel 2011]
... ... ...
... ...
Clustering blind to experimental conditions
G Varoquaux 9

18. 2 Random parcellations and
sparsity
Combining
Clustering
Sparsity
G Varoquaux 10

19. 2 Random parcellations and
sparsity
+
Randomization
Stability scores
G Varoquaux 10

20. 2 Algorithm
1 loop: perturb randomly data
2 Ward agglomeration to form n features
3 sparse linear model on reduced features
4 accumulate non-zero features
5 threshold map of apparition counts
G Varoquaux 11

21. 2 Recovery performance
RandomizedClusteredLasso:
Selection scores
max
0
G Varoquaux 12

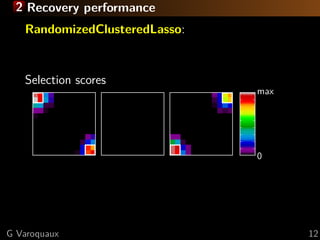
22. 2 What is the best method for feature recovery?
For small brain regions: elastic net
For large brain regions: randomized-clustered sparsity
Large regions and very smooth images: F-tests
[Varoquaux 2012] ICML
G Varoquaux 13

23. 2 fMRI: face vs house discrimination [Haxby 2001]
F-scores
L R
L R
y=-31 x=17
z=-17
G Varoquaux 14

24. 2 fMRI: face vs house discrimination [Haxby 2001]
Randomized Clustered Sparsity
L R
L R
y=-31 x=17
z=-17
Less background noise
(source of false positive)
G Varoquaux 14

25. 2 Predictive power of selected voxels
Object recognition [Haxby 2001]
Using recovered voxels improves prediction
G Varoquaux 15

26. Can we recover meaningful spatial information
from multivariate pattern analysis?
SVM and sparse models less powerful then F-score
Sparsity + clustering + randomization:
excellent recovery
⇒ Multivariate brain mapping
Simultaneous prediction and recovery
Prediction
accuracy:
93%
G Varoquaux 16

27. For more details
G. Varoquaux, A. Gramfort, and B. Thirion, Small-sample
brain mapping: sparse recovery on spatially correlated de-
signs with randomization and clustering, ICML 2012
Acknowledgments, for sharing data:
J. Haxby R. Poldrack K. Jimura
Software
scikit-learn: machine learning in Python
G Varoquaux 17