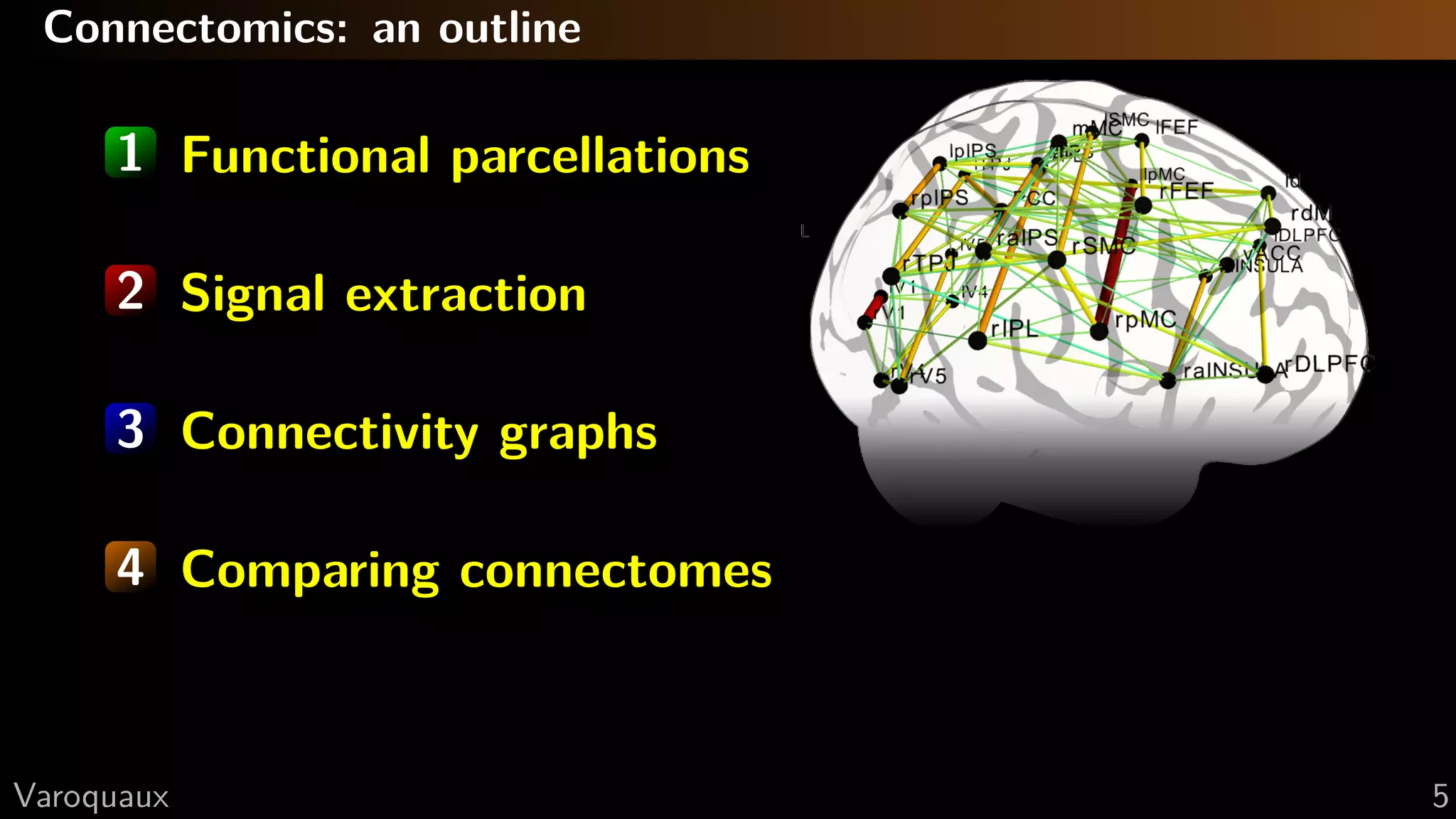
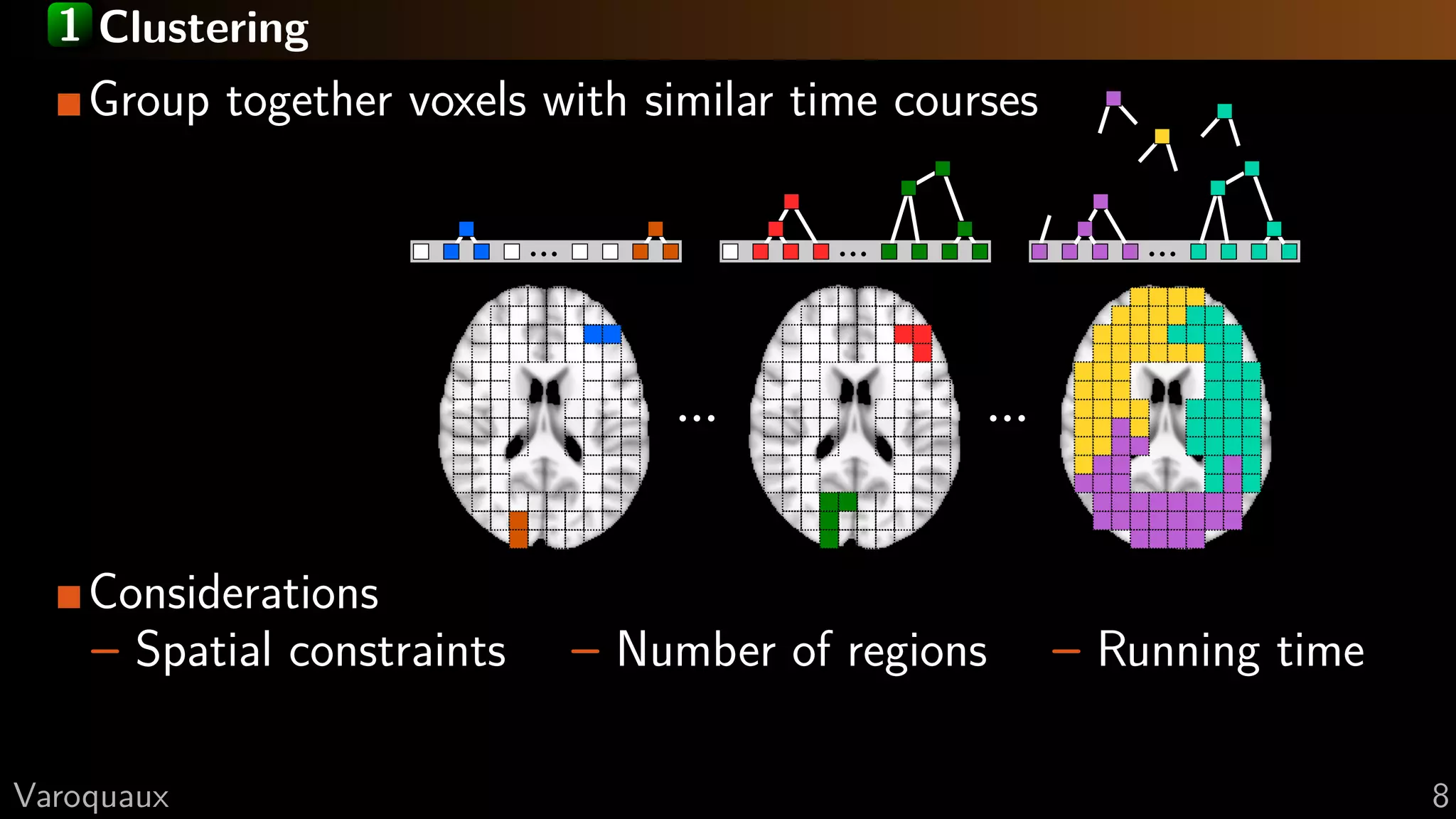
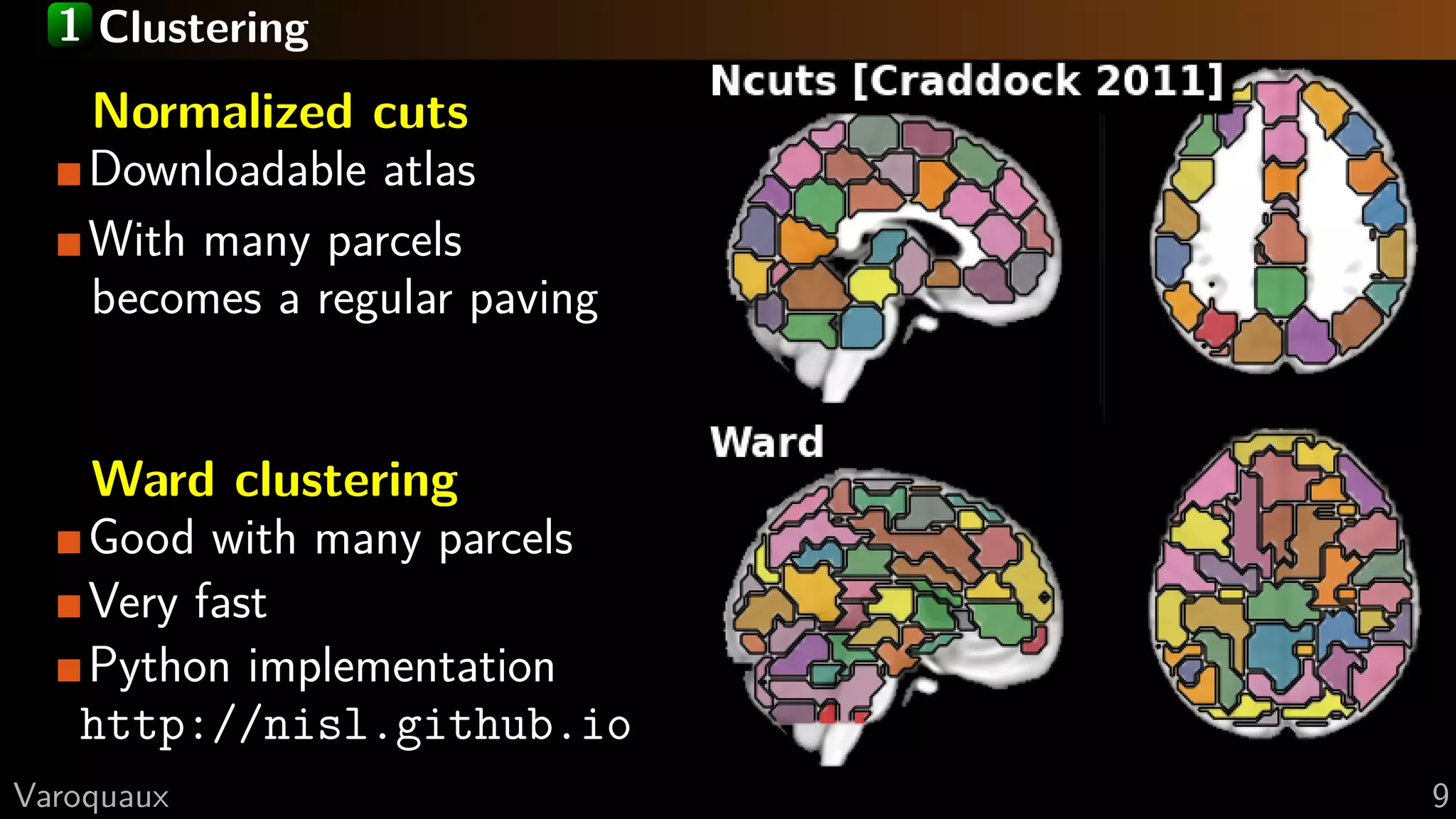
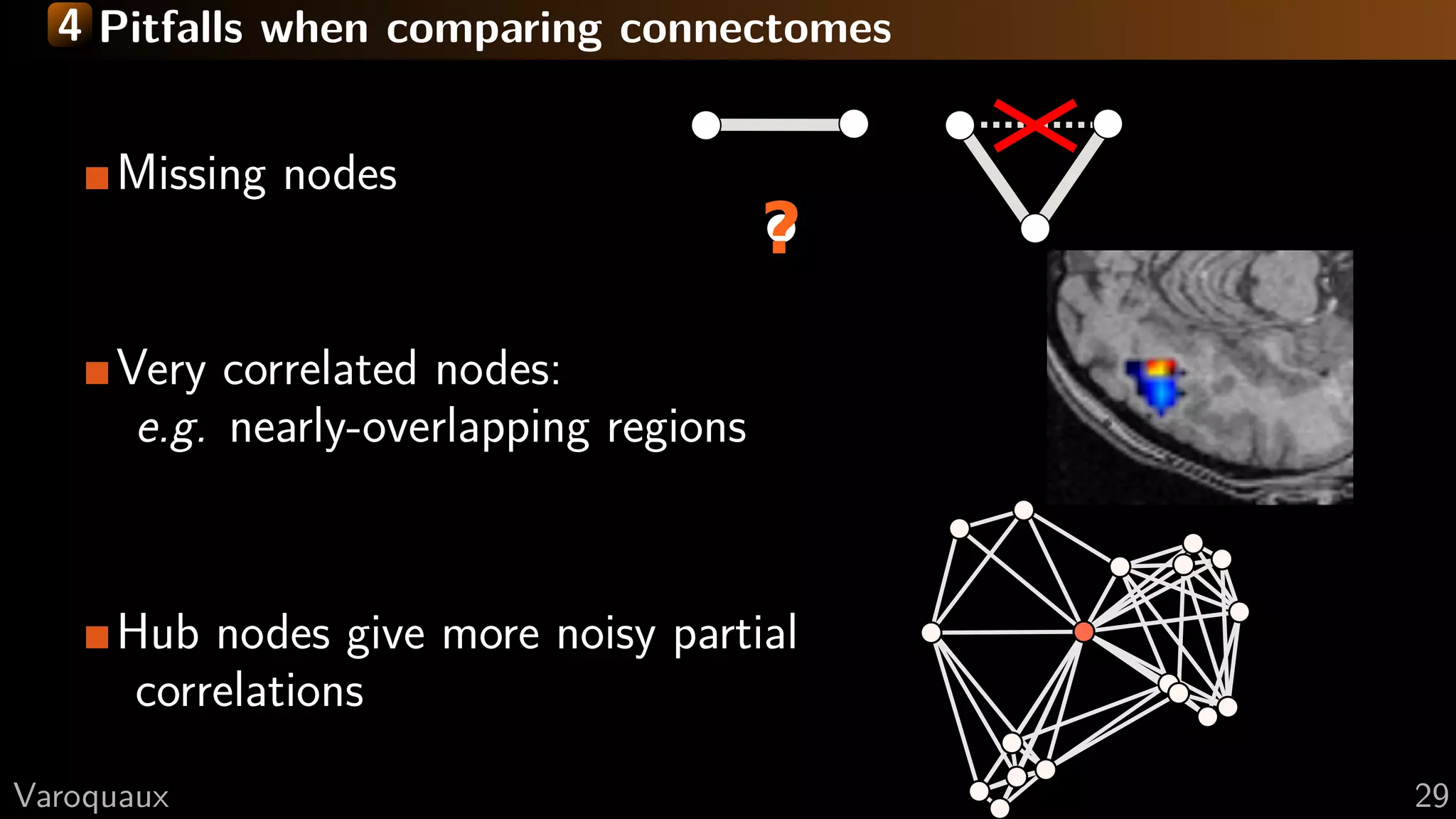
The document focuses on connectomics, specifically methodologies for parcellation and network analysis in the context of functional connectivity. It emphasizes the importance of selecting appropriate regions for connectivity analysis, extracting signal, and comparing connectomes, highlighting challenges such as statistical problems with too many regions and the need for confound regression. The document concludes with practical recommendations and references relevant research in the field.






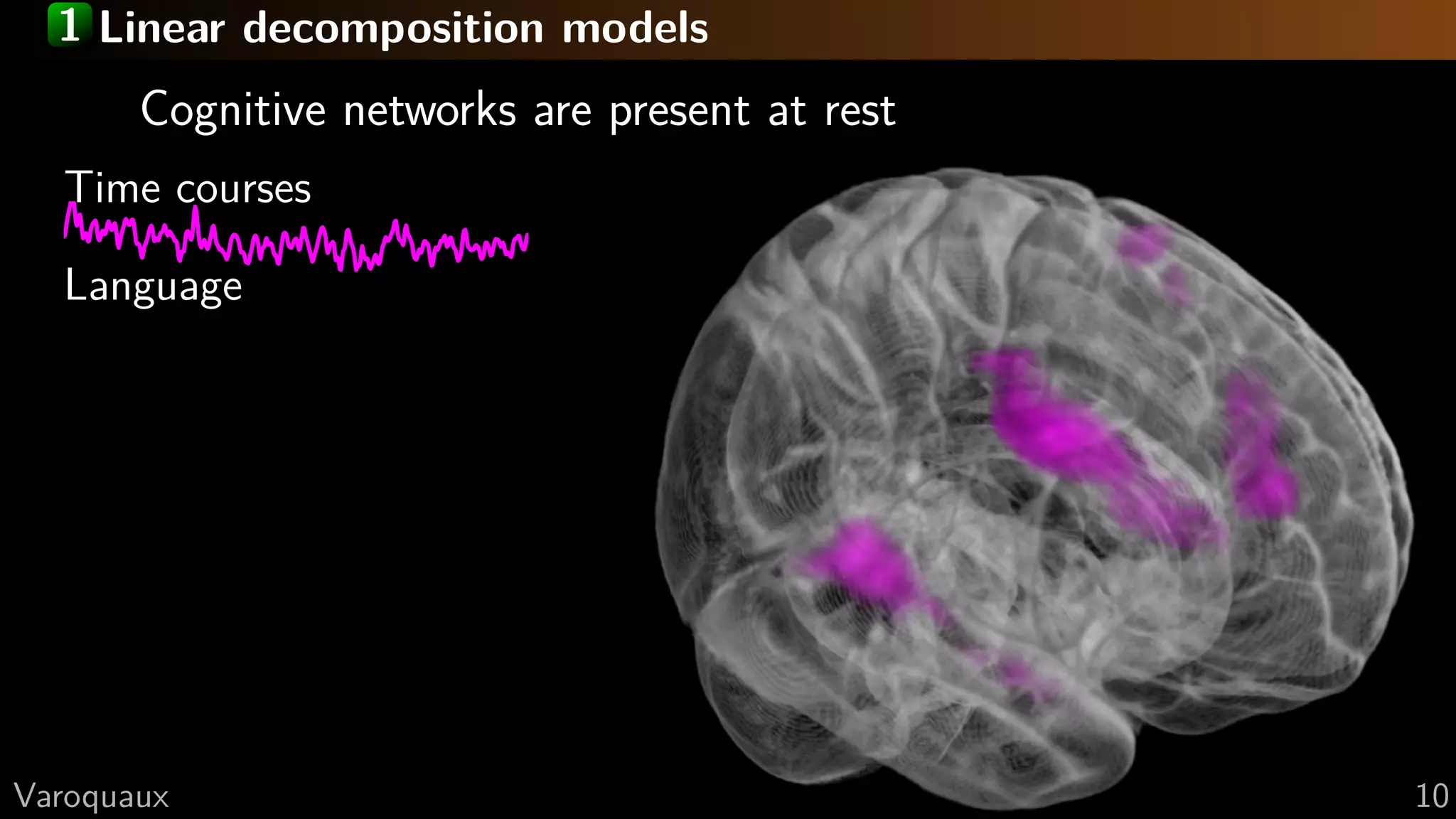

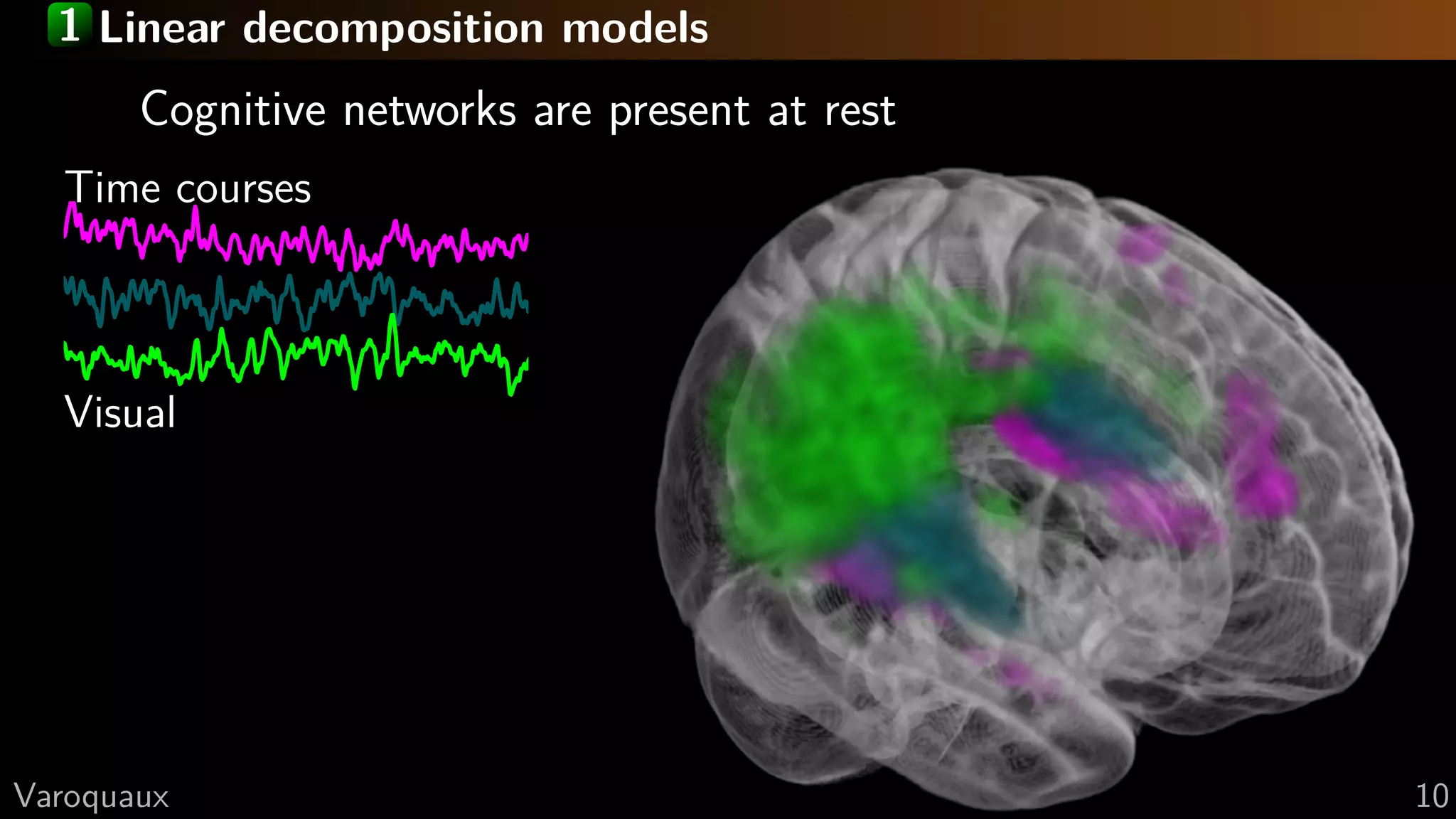






![1 Linear decomposition models
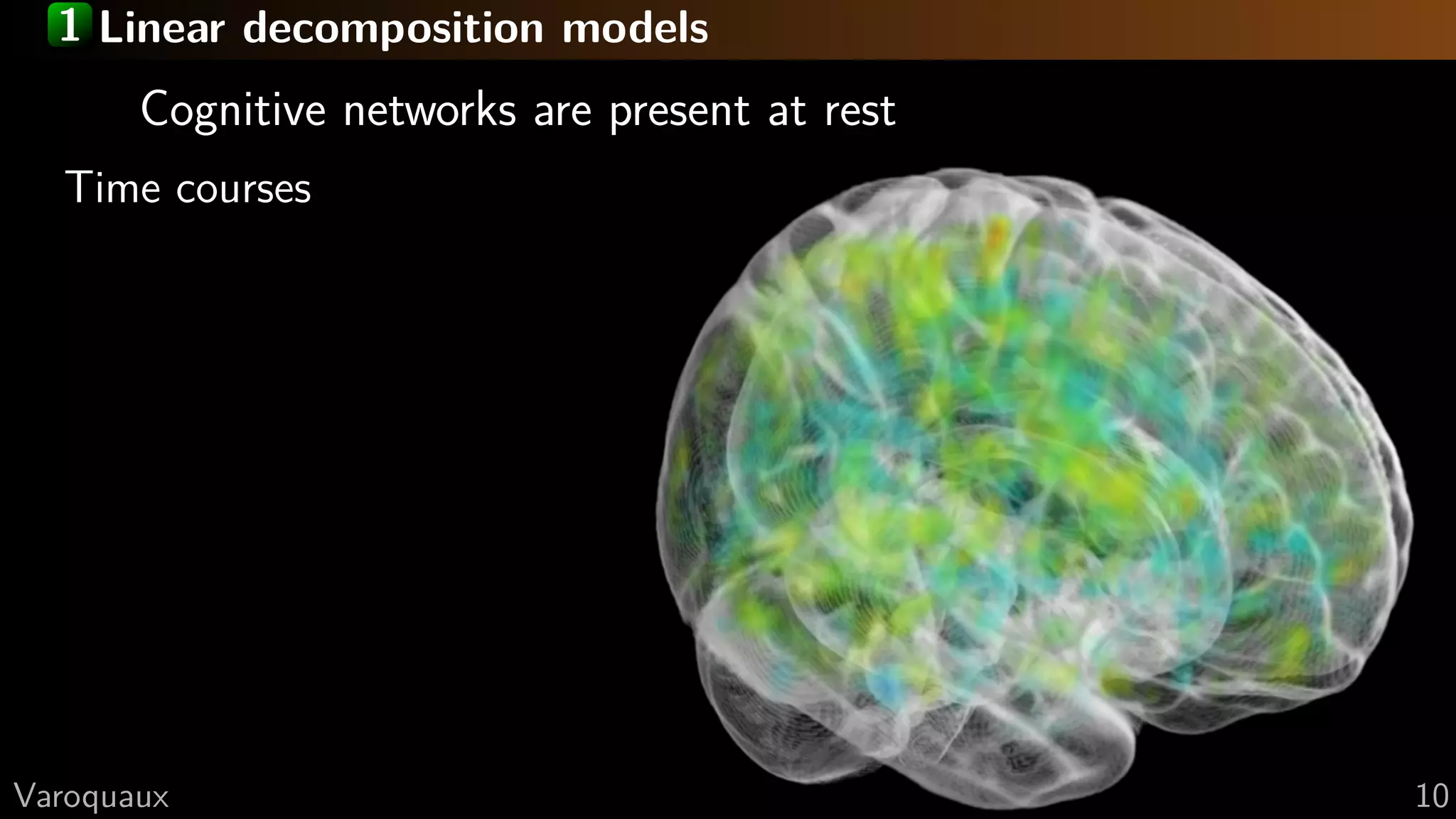
Independent Component Analysis
Extracts networks
Downloadable atlas
[Smith 2009]
Sparse dictionary learning
Networks outlined cleanly
Bleeding edge
Atlas on request
G Varoquaux 11](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-20-2048.jpg)
![1 Linear decomposition models
Independent Component Analysis
Extracts networks
Downloadable atlas
[Smith 2009]
Sparse dictionary learning
Networks outlined cleanly
Bleeding edge
Atlas on request
G Varoquaux 11](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-21-2048.jpg)


![2 Time-series extraction
Extract ROI-average signal:
weighted-mean with weights
given by grey-matter probability
Regress out confounds:
- movement parameters
- CSF and white matter signals
- Compcorr: data-driven noise identification
[Behzadi 2007]
- Global mean... overhyped discussion (see later)
G Varoquaux 14](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-24-2048.jpg)

![3 Correlation, covariance
1
For x and y centered:
covariance: cov(x, y) =
1
n i
xiyi
correlation: cor(x, y) =
cov(x, y)
std(x) std(y)
Correlation is normalized: cor(x, y) ∈ [−1, 1]
Quantify linear dependence between x and y
Correlation matrix
functional connectivity graphs
[Bullmore1996, Achard2006...]
G Varoquaux 16](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-26-2048.jpg)
![3 Partial correlation
Remove the effect of z by regressing it out
x/z = residuals of regression of x on z
In a set of p signals,
partial correlation: cor(xi/Z, xj/Z), Z = {xk, k = i, j}
partial variance: var(xi/Z), Z = {xk, k = i}
Partial correlation matrix
[Marrelec2006, Fransson2008, ...]
G Varoquaux 17](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-27-2048.jpg)
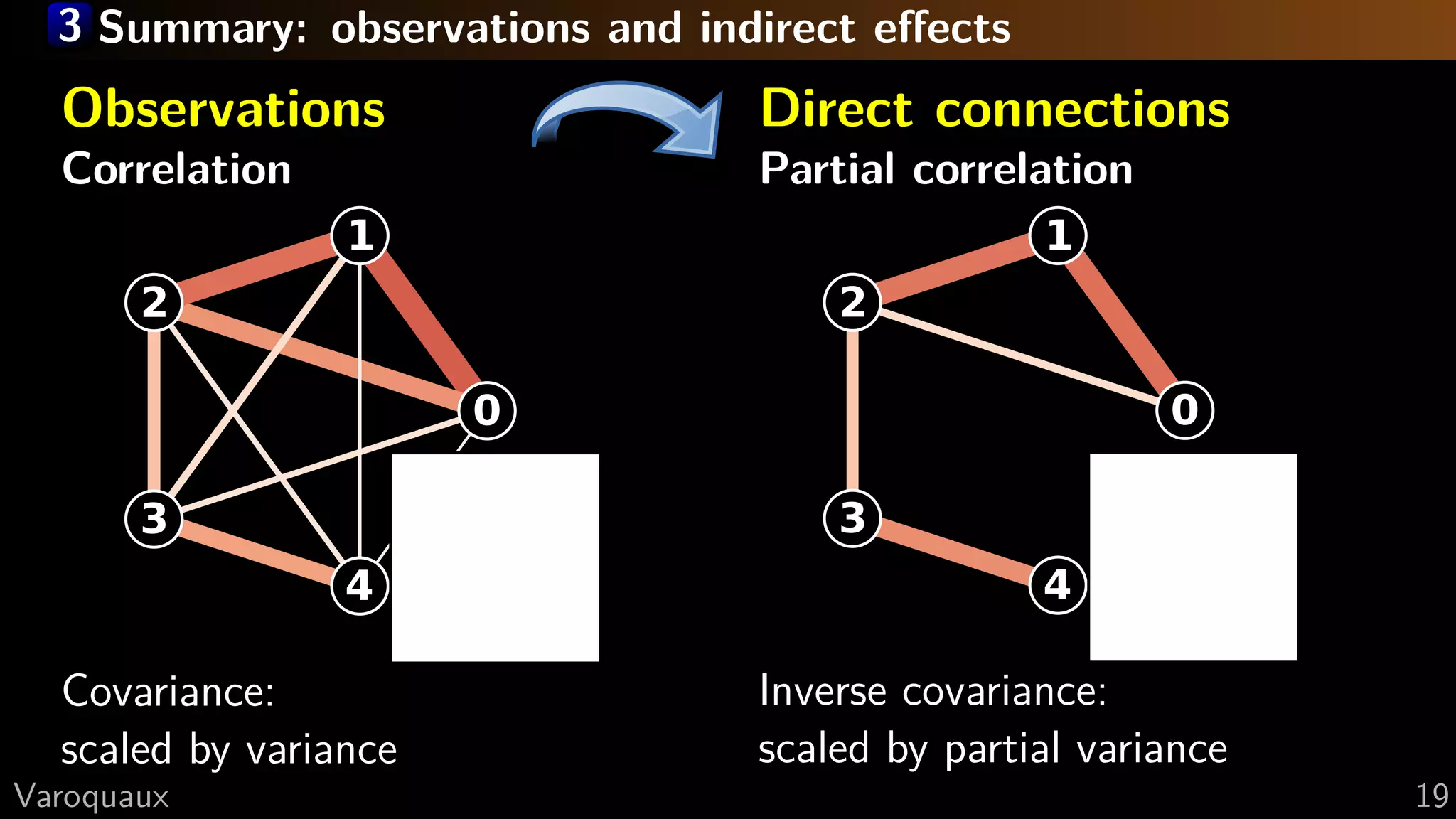
![3 Inverse covariance
K = Matrix inverse of the covariance matrix
On the diagonal: partial variance
Off diagonal: scaled partial correlation
Ki,j = −cor(xi/Z, xj/Z) std(xi/Z) std(xj/Z)
Inverse covariance matrix
[Smith 2011, Varoquaux NIPS 2010, ...]
G Varoquaux 18](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-28-2048.jpg)





![3 Inverse covariance matrix estimation
Sparse Inverse Covariance estimators: Independence between
nodes makes estimation of partial correlation easier
0
1
2
3
4
Independence
structure
+ 0
1
2
3
4
Connectivity
values
Joint estimation
Group-sparse inverse covariance: learn different connectomes
with same independence structure
[Varoquaux, NIPS 2010]
G Varoquaux 22](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-35-2048.jpg)
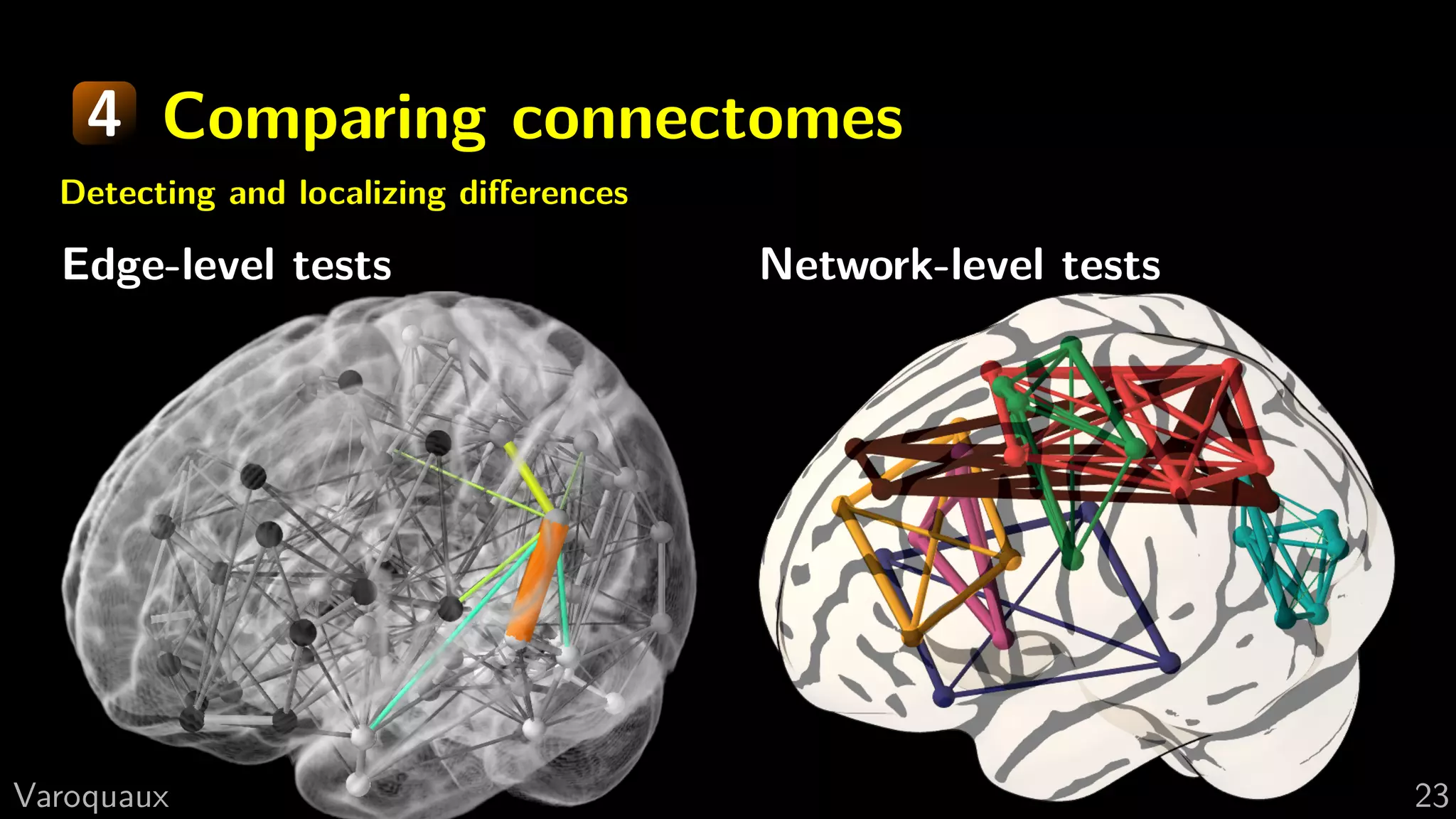
![4 Pair-wise tests on correlations
Correlations ∈ [−1, 1]
⇒ cannot apply Gaussian
statistics, e.g. T tests
Z-transform:
Z = arctanh cor =
1
2
ln
1 + cor
1 − cor
Z(cor) is normaly-distributed:
For n observations, Z(cor) = N
Z(cor),
1
√
n
G Varoquaux 24](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-38-2048.jpg)
![4 Indirect effects: to partial or not to partial?
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25Large lesion
Correlation matrices
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25Large lesion
Partial correlation matrices
Spread-out variability in correlation matrices
Noise in partial-correlations
Strong dependence between coefficients
[Varoquaux MICCAI 2010]G Varoquaux 25](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-39-2048.jpg)
![4 Indirect effects versus noise: a trade off
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25Large lesion
Correlation matrices
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25Large lesion
Partial correlation matrices
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25 Control
0 5 10 15 20 25
0
5
10
15
20
25Large lesion
Tangent-space residuals
[Varoquaux MICCAI 2010]
G Varoquaux 26](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-40-2048.jpg)


![4 Network-level metrics
Network-wide activity
Quantify amount of signal in Σnetwork
Determinant: |Σnetwork|
= generalized variance
Network integration: = log |ΣA|
Cross-talk between network A and B
Mutual information
= log |ΣAB| − log |ΣA| − log |ΣB|
[Marrelec 2008, Varoquaux NIPS 2010]G Varoquaux 28](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-43-2048.jpg)
![Practical connectomics: take home messages
Need to choose
functionally-relevent regions
Regress confounds out from signals
Partial correlations to isolate
direct effects
Networks are interesting units
for comparison
http://gael-varoquaux.info [NeuroImage 2013]](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-45-2048.jpg)
![References (not exhaustive)
[Achard 2006] A resilient, low-frequency, small-world human brain functional network
with highly connected association cortical hubs, J Neurosci
[Behzadi 2007] A component based noise correction method (CompCor) for BOLD
and perfusion based fMRI, NeuroImage
[Bullmore 2009] Complex brain networks: graph theoretical analysis of structural
and functional systems, Nat Rev Neurosci
[Craddock 2011] A Whole Brain fMRI Atlas Generated via Spatially Constrained
Spectral Clustering, Hum Brain Mapp
[Frasson 2008] The precuneus/posterior cingulate cortex plays a pivotal role in the
default mode network: Evidence from a partial correlation network analysis,
NeuroImage
[Marrelec 2006] Partial correlation for functional brain interactivity investigation in
functional MRI, NeuroImage
[Marrelec 2008] Regions, systems, and the brain: hierarchical measures of functional
integration in fMRI, Med Im Analys](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-46-2048.jpg)
![References (not exhaustive)
[Smith 2010] Network Modelling Methods for fMRI, NeuroImage
[Smith 2009] Correspondence of the brain’s functional architecture during activation
and rest, PNAS
[Varoquaux MICCAI 2010] Detection of brain functional-connectivity difference in
post-stroke patients using group-level covariance modeling, Med Imag Proc Comp
Aided Intervention
[Varoquaux NIPS 2010] Brain covariance selection: better individual functional
connectivity models using population prior, Neural Inf Proc Sys
[Varoquaux 2011] Multi-subject dictionary learning to segment an atlas of brain
spontaneous activity, IPMI
[Varoquaux 2012] Markov models for fMRI correlation structure: is brain functional
connectivity small world, or decomposable into networks?, J Physio Paris
[Varoquaux 2013] Learning and comparing functional connectomes across subjects,
NeuroImage](https://image.slidesharecdn.com/slides-130422085753-phpapp01/75/Connectomics-Parcellations-and-Network-Analysis-Methods-47-2048.jpg)