The document provides an overview of imprecision in statistical learning, focusing on the implications of having imprecise data, models, and predictions within a learning framework. It discusses model selection through loss minimization, the challenges faced when data or models are imprecise, and various approaches to define optimal models in uncertain settings. Additionally, it explores the effects of imprecision on both inductive processes and predictions, emphasizing the importance of context in choosing either optimistic or pessimistic strategies for model evaluation.






![Imprecision in learning Imprecise data (and precise models)
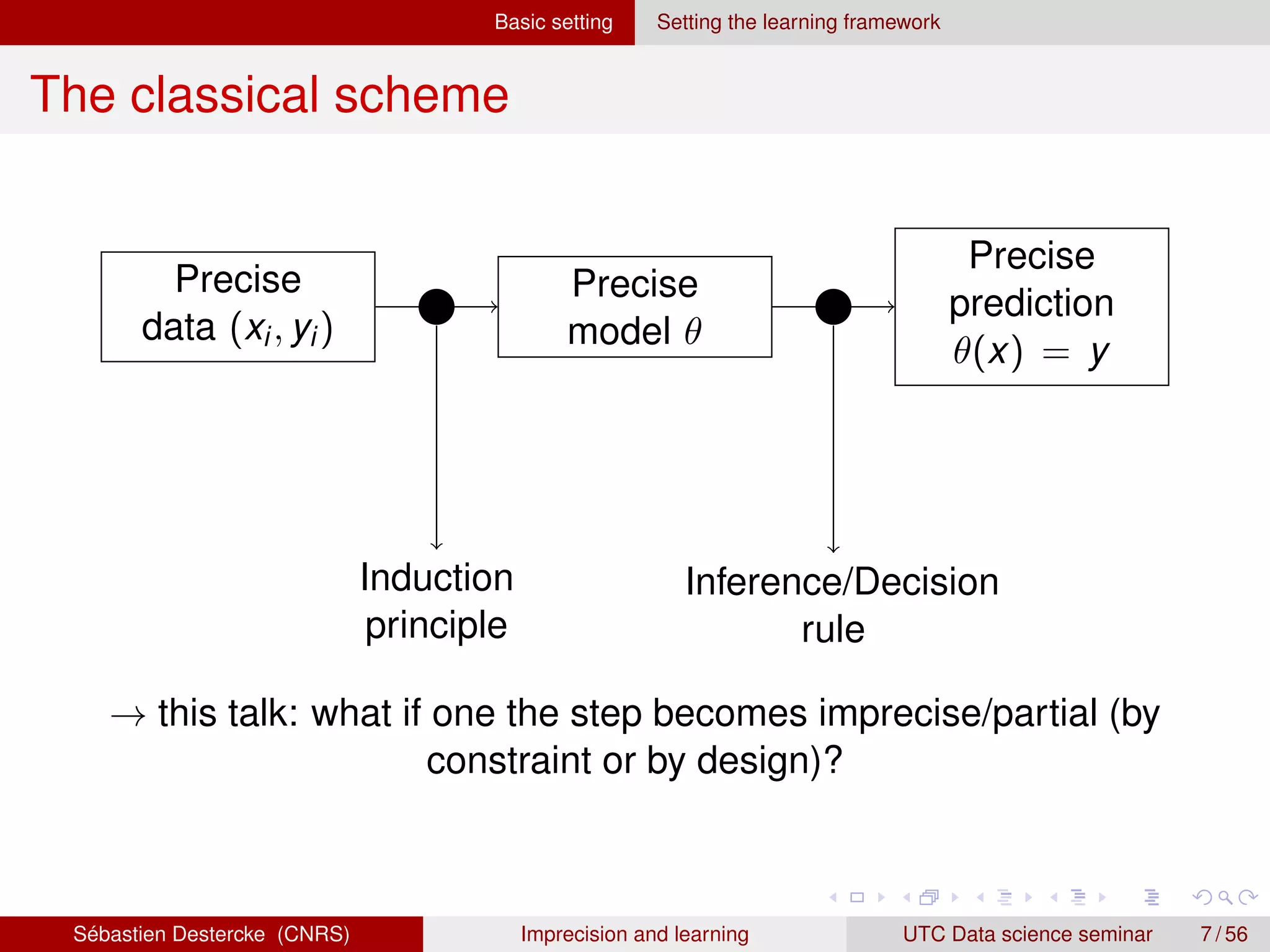
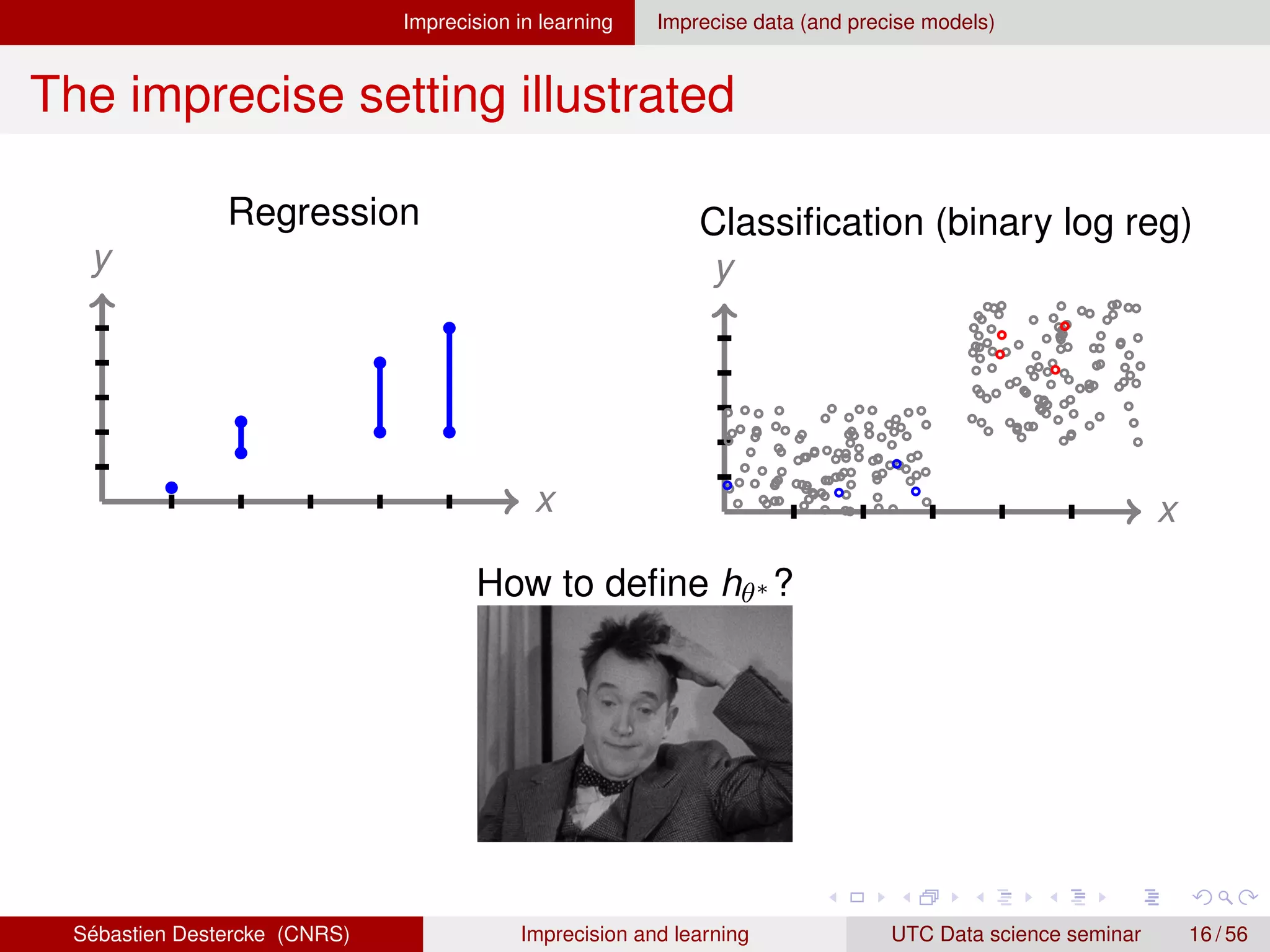
Induction with imprecise data
We observe possibly imprecise input/output (X, Y) containing the
truth (one (x, y) ∈ (X, Y) are true, unobserved values)
Losses3 both become set-valued [2]:
`(θ(X), Y) = {`(θ(X), Y)|y ∈ Y, x ∈ X}
Previous induction principles are no longer well-defined
What if we still want to get one model?
3
And likelihoods/posteriors alike
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 15 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-15-2048.jpg)
![Imprecision in learning Imprecise data (and precise models)
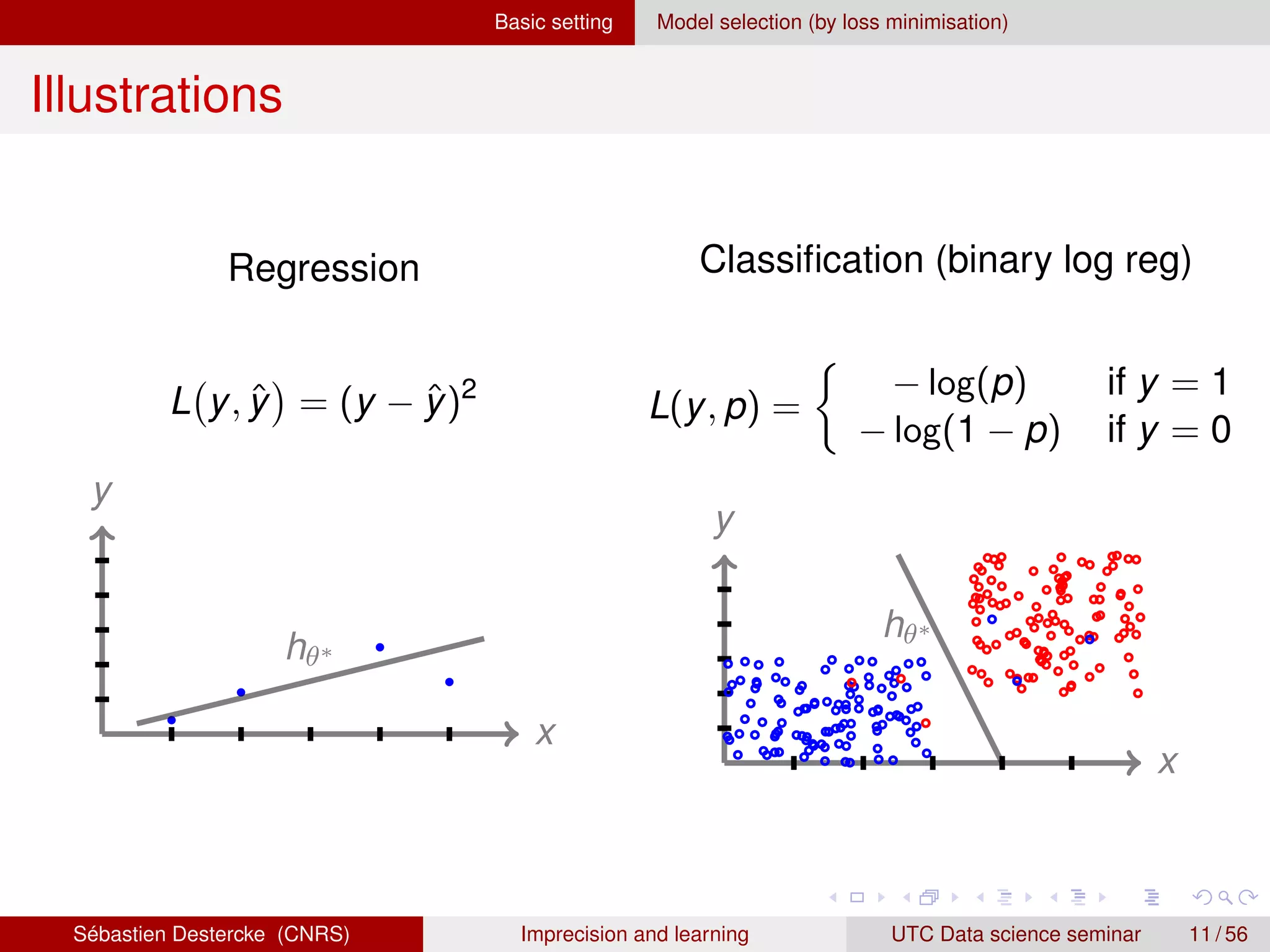
Illustration on toy example
`0/1(ŷ, y)
R(θ) =
P
i min(xi ,yi )∈(Xi ,Yi ) `(θ(xi), yi) → best case scenario
R(θ) =
P
i max(xi ,yi )∈(Xi ,Yi ) `(θ(xi), yi) → worst case scenario
X1
X2
1 2
3
4
5
θ2
θ1
[R(θ1), R(θ1)] = [0, 5/13]
[R(θ2), R(θ2)] = [1/13, 3/13]
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 17 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-17-2048.jpg)
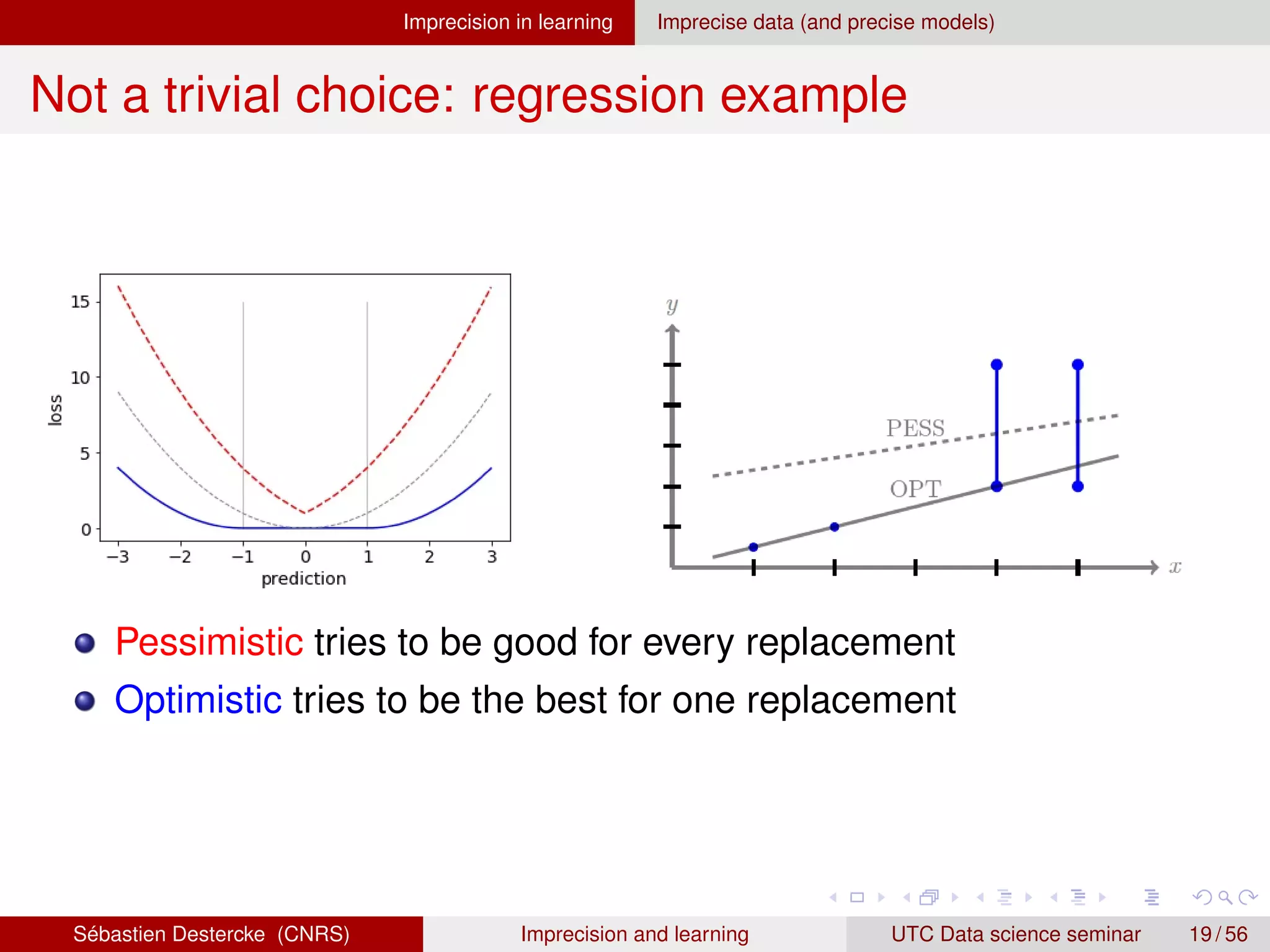
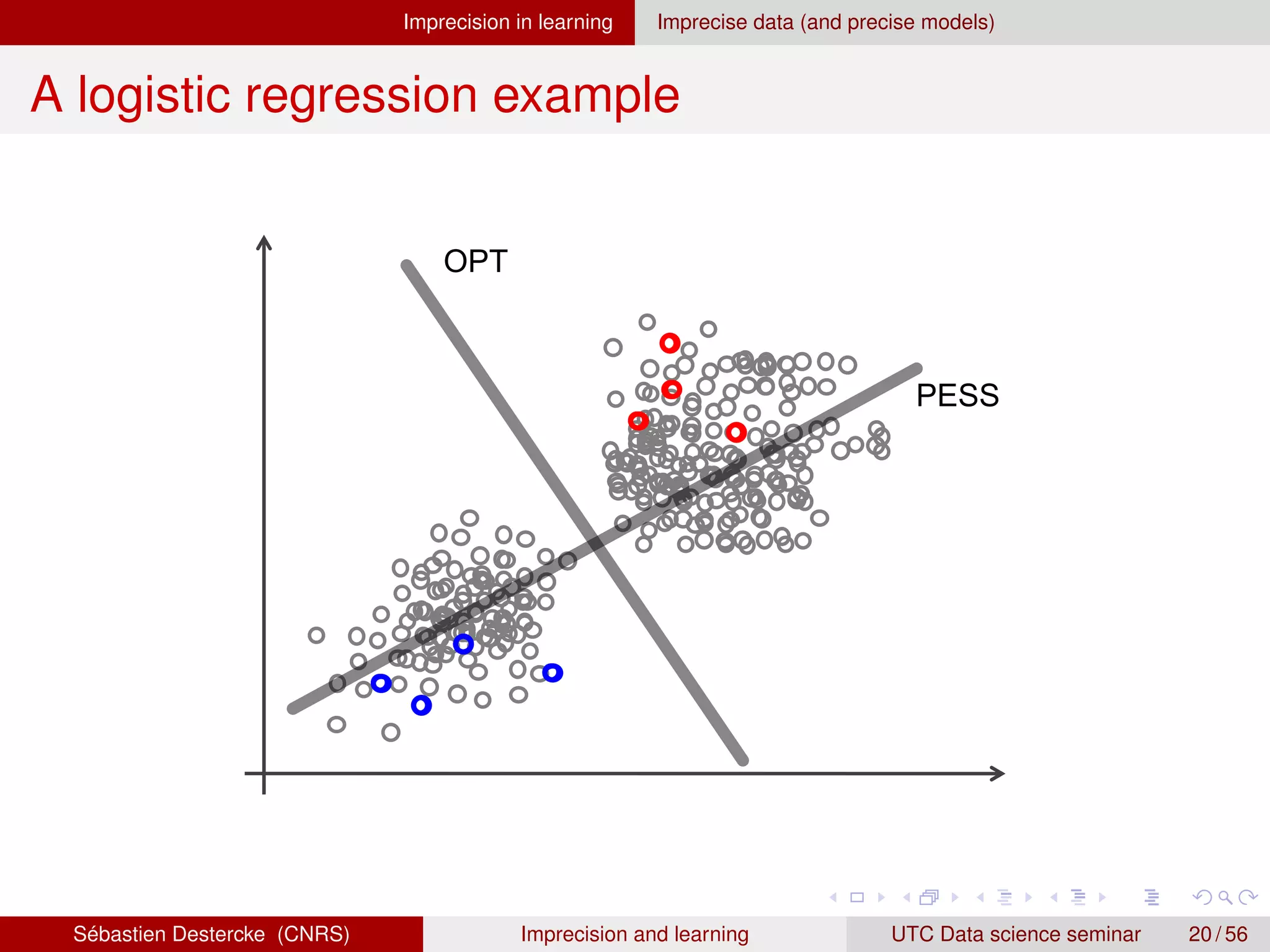
![Imprecision in learning Imprecise data (and precise models)
Going back to a precise model
If we know the “imprecisiation” process Pobs((X, Y)|(x, y)), no
theoretical problem → “merely” a computational one
If not, common approaches are to redefine a precise criterion:
Optimistic (Maximax/Minimin) approach [8, 1]:
`opt (θ(x), Y) = min{`(θ(x), Y)|y ∈ Y}
Pessimistic (Maximin/Minimax) approach [6]:
`pes(θ(x), Y) = max{`(θ(x), Y)|y ∈ Y}
EM-like or averaging/weighting approaches4
approach
`w (θ(x), Y) =
X
y∈Y
wy `(θ(x), y),
4
With likelihood ∼ Lav (θ|(x, Y)) = P((x, Y)|θ) [4]
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 18 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-18-2048.jpg)




![Imprecision in learning Imprecision in models
Back to the toy example
`0/1(ŷ, y)
Unless we commit to a behaviour, models θ1, θ2 incomparable
X1
X2
1 2
3
4
5
θ2
θ1
[R(θ1), R(θ1)] = [0, 5/13]
[R(θ2), R(θ2)] = [1/13, 3/13]
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 29 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-30-2048.jpg)
![Imprecision in learning Imprecision in models
Induced partial order
Each model is now set- or interval-valued
θ1 θ2 θ3 θn
[R(θ1), R(θ1)] [R(θ2), R(θ2)] [R(θ3), R(θ3)] [R(θn), R(θn)]
θi θj for sure if R(θi) R(θj)
this is known as an interval-order
(very) safe bet: take all maximal models θ, i.e., without θ0 θ
works also if [R(θi), R(θi)] is a statistical confidence interval
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 30 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-31-2048.jpg)
![Imprecision in learning Imprecision in models
Sets of best models
Not taking the best, but the k-best
θ(1) θ(2) θ(3) θ(k) θ(k+1)
R(θ(1)) R(θ(2)) R(θ(3)) R(θ(k)) R(θ(k+1))
One common way to do it [5] (dates back to Birnbaum, at least):
Normalize likelihood by computing
L∗
(θ|(x·, y·)) =
L(θ|(x·, y·))
arg supθ L(θ|(x·, y·))
Take as set estimate cut of level α
Θα = {θ|L∗
(θ|(x·, y·)) ≥ α}
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 32 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-33-2048.jpg)
![Imprecision in learning Imprecision in models
Robust Bayes and imprecise probabilities [12, 14]
Consider a set of priors, and its corresponding set of posteriors
θ(1) θ(2) θ(3) θ(n)
R(θ(1)) R(θ(2)) R(θ(3)) R(θ(n))
[P(θ1), P(θ1)] [P(θ2), P(θ2)] [P(θ3), P(θ3)] [P(θn), P(θn)]
6= from pure Bayesian approach, as priors are not weighted5
5
Anarchy!
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 33 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-34-2048.jpg)
![Imprecision in learning Imprecision in models
Other reasons
You want to make some robustness analysis around your top
models or your weighting scheme (because of limited data, of the
fact that they are not the theoretical optimal ones, . . . );
You suspect the observed data will be different6 from the training
ones (transfer learning, distributional robustness [9]);
You want a rich uncertainty quantification where there is a clear
distinction between aleatory uncertainty (irreducible, due to fixed
learning setting) and epistemic uncertainty (reducible by collecting
information). This can be used to:
produce cautious predictions (see next slides)
perform active learning [10]
explain uncertainty sources (largely unexplored topic)
6
In practice, issued from a distribution Ptest (X, Y) 6= Ptrain(X, Y)
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 36 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-37-2048.jpg)
![Imprecision in learning Imprecision in models
Two kinds of uncertainties
Aleatory uncertainty: classes are really mixed → irreducible with
more data (but possibly by adding features)
Epistemic uncertainty: lack of information → reducible
X2
X1
x
a
a
a
b
b
b
Aleatory uncertainty
P(a) ∈ [0.45, 0.55]
X2
X1
x
a
b
Epistemic uncertainty
P(a) ∈ [0.2, 0.8]
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 37 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-38-2048.jpg)
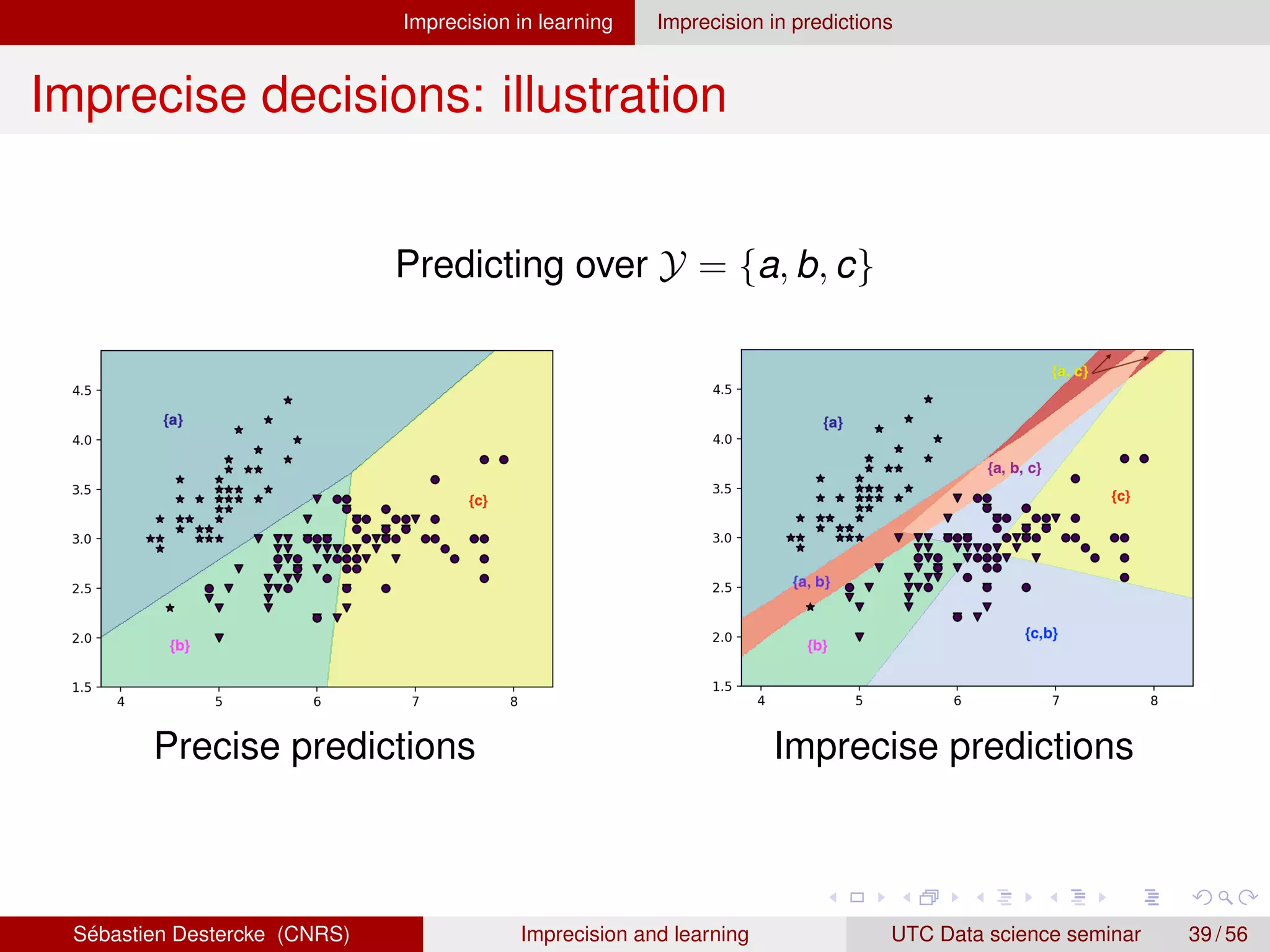
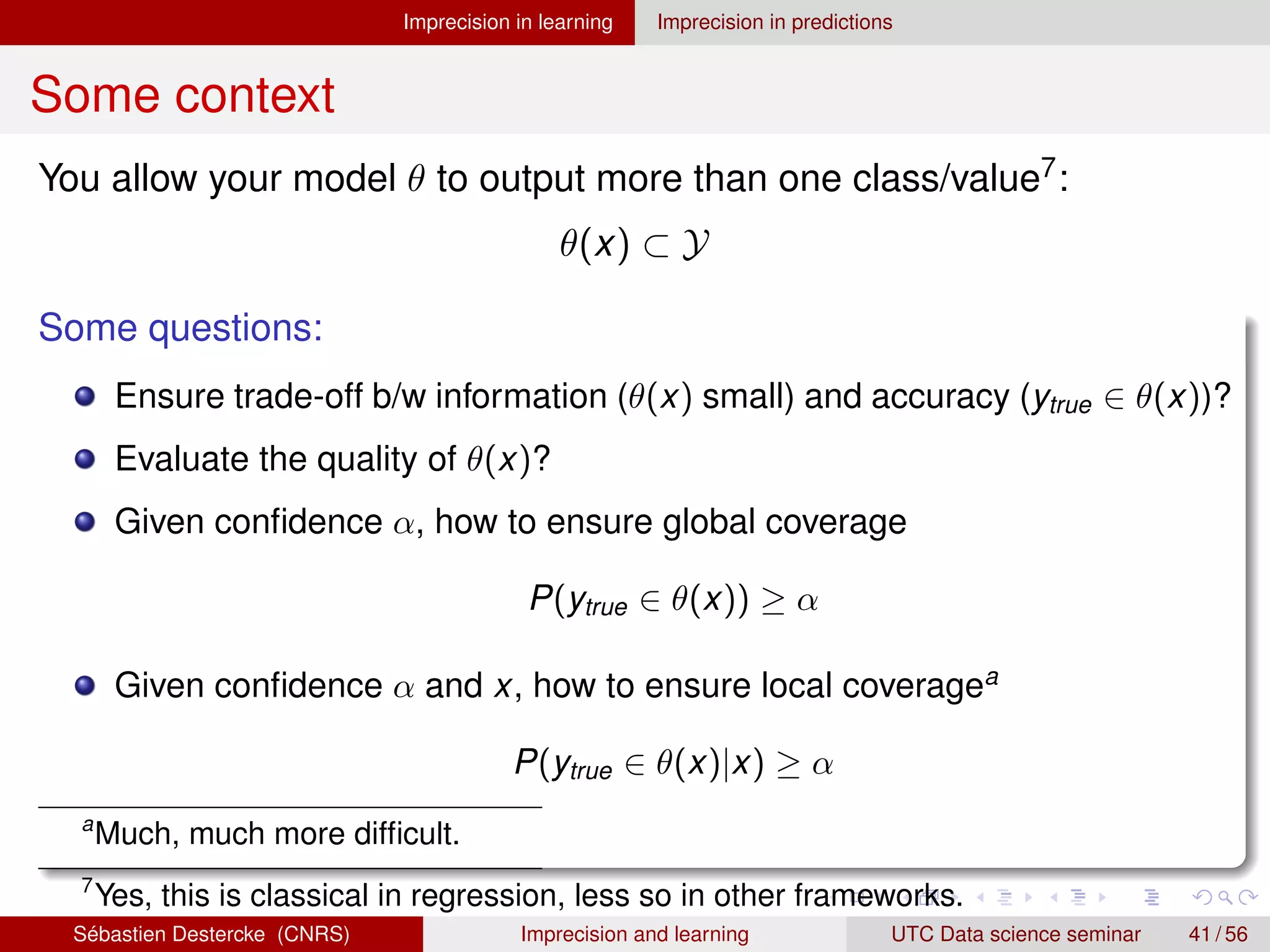
![Imprecision in learning Imprecision in predictions
Probabilistic partial reject [3, 7]
Assume we have p(y|x) as training output
Fix a confidence value α ∈ [0, 1]
Consider the permutation () on Y such that
p(y(1)
|x) ≥ p(y(2)
|x) ≥ . . . ≥ p(y(K)
|x)
Take all classes until cumulated probability is above
θ(x) = {y(1)
, . . . , y(j)
:
j−1
X
i=1
p(y(i)
|x) ≤ α,
j
X
i=1
p(y(i)
|x) ≥ α}
Example
α = 0.9
P(a|x) = 0.7, P(b|x) = 0.05, P(c|x) = 0.25
θ(x) =
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 42 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-43-2048.jpg)
![Imprecision in learning Imprecision in predictions
Probabilistic partial reject [3, 7]
Assume we have p(y|x) as training output
Fix a confidence value α ∈ [0, 1]
Consider the permutation () on Y such that
p(y(1)
|x) ≥ p(y(2)
|x) ≥ . . . ≥ p(y(K)
|x)
Take all classes until cumulated probability is above
θ(x) = {y(1)
, . . . , y(j)
:
j−1
X
i=1
p(y(i)
|x) ≤ α,
j
X
i=1
p(y(i)
|x) ≥ α}
Example
α = 0.9
P(a|x) = 0.7 P(c|x) = 0.25 P(b|x) = 0.05
θ(x) = {a, c}
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 42 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-44-2048.jpg)

![Imprecision in learning Imprecision in predictions
(inductive) Conformal prediction [11]
Take a validation set9 of I instances (xi, yi)
To each yi associate a score αi = maxy6=yi
(p(y|xi) − p(yi|xi))
Given new instance xI+1, define p-value of each prediction yj as
pv(yj
) =
|{i = 1, . . . , I, I + 1 : αi ≥ αyj
}|
n + 1
.
with αyj
score of (xI+1, yj)
Fix a confidence value α ∈ [0, 1]
Get as prediction
θ(x) = {yj
: pv(yj
) ≥ 1 − α}.
9
6= training and test sets
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 44 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-46-2048.jpg)










![Imprecision in learning Imprecision in predictions
References I
[1] Timothee Cour, Ben Sapp, and Ben Taskar.
Learning from partial labels.
Journal of Machine Learning Research, 12(May):1501–1536, 2011.
[2] Inés Couso and Luciano Sánchez.
Machine learning models, epistemic set-valued data and generalized loss functions: An encompassing approach.
Information Sciences, 358:129–150, 2016.
[3] Juan José del Coz, Jorge Díez, and Antonio Bahamonde.
Learning nondeterministic classifiers.
Journal of Machine Learning Research, 10(Oct):2273–2293, 2009.
[4] Thierry Denoeux.
Maximum likelihood estimation from uncertain data in the belief function framework.
IEEE Transactions on knowledge and data engineering, 25(1):119–130, 2013.
[5] D. Dubois, S. Moral, and H. Prade.
A semantics for possibility theory based on likelihoods,.
Journal of Mathematical Analysis and Applications, 205(2):359 – 380, 1997.
[6] Romain Guillaume, Inés Couso, and Didier Dubois.
Maximum likelihood with coarse data based on robust optimisation.
In Proceedings of the Tenth International Symposium on Imprecise Probability: Theories and Applications, pages 169–180,
2017.
[7] Thien M Ha.
The optimum class-selective rejection rule.
IEEE Transactions on Pattern Analysis and Machine Intelligence, 19(6):608–615, 1997.
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 54 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-59-2048.jpg)
![Imprecision in learning Imprecision in predictions
References II
[8] Eyke Hüllermeier.
Learning from imprecise and fuzzy observations: Data disambiguation through generalized loss minimization.
International Journal of Approximate Reasoning, 55(7):1519–1534, 2014.
[9] Daniel Kuhn, Peyman Mohajerin Esfahani, Viet Anh Nguyen, and Soroosh Shafieezadeh-Abadeh.
Wasserstein distributionally robust optimization: Theory and applications in machine learning.
In Operations Research Management Science in the Age of Analytics, pages 130–166. INFORMS, 2019.
[10] Vu-Linh Nguyen, Sébastien Destercke, and Eyke Hüllermeier.
Epistemic uncertainty sampling.
In International Conference on Discovery Science, pages 72–86. Springer, 2019.
[11] Harris Papadopoulos.
Inductive conformal prediction: Theory and application to neural networks.
In Tools in artificial intelligence. Citeseer, 2008.
[12] P. Walley.
Statistical reasoning with imprecise Probabilities.
Chapman and Hall, New York, 1991.
[13] Gen Yang, Sébastien Destercke, and Marie-Hélène Masson.
The costs of indeterminacy: How to determine them?
IEEE transactions on cybernetics, 47(12):4316–4327, 2017.
[14] M. Zaffalon.
The naive credal classifier.
J. Probabilistic Planning and Inference, 105:105–122, 2002.
[15] Marco Zaffalon, Giorgio Corani, and Denis Mauá.
Evaluating credal classifiers by utility-discounted predictive accuracy.
International Journal of Approximate Reasoning, 53(8):1282–1301, 2012.
Sébastien Destercke (CNRS) Imprecision and learning UTC Data science seminar 55 / 56](https://image.slidesharecdn.com/hdslearningimprecision-210602094220/75/Imprecision-in-learning-an-overview-60-2048.jpg)