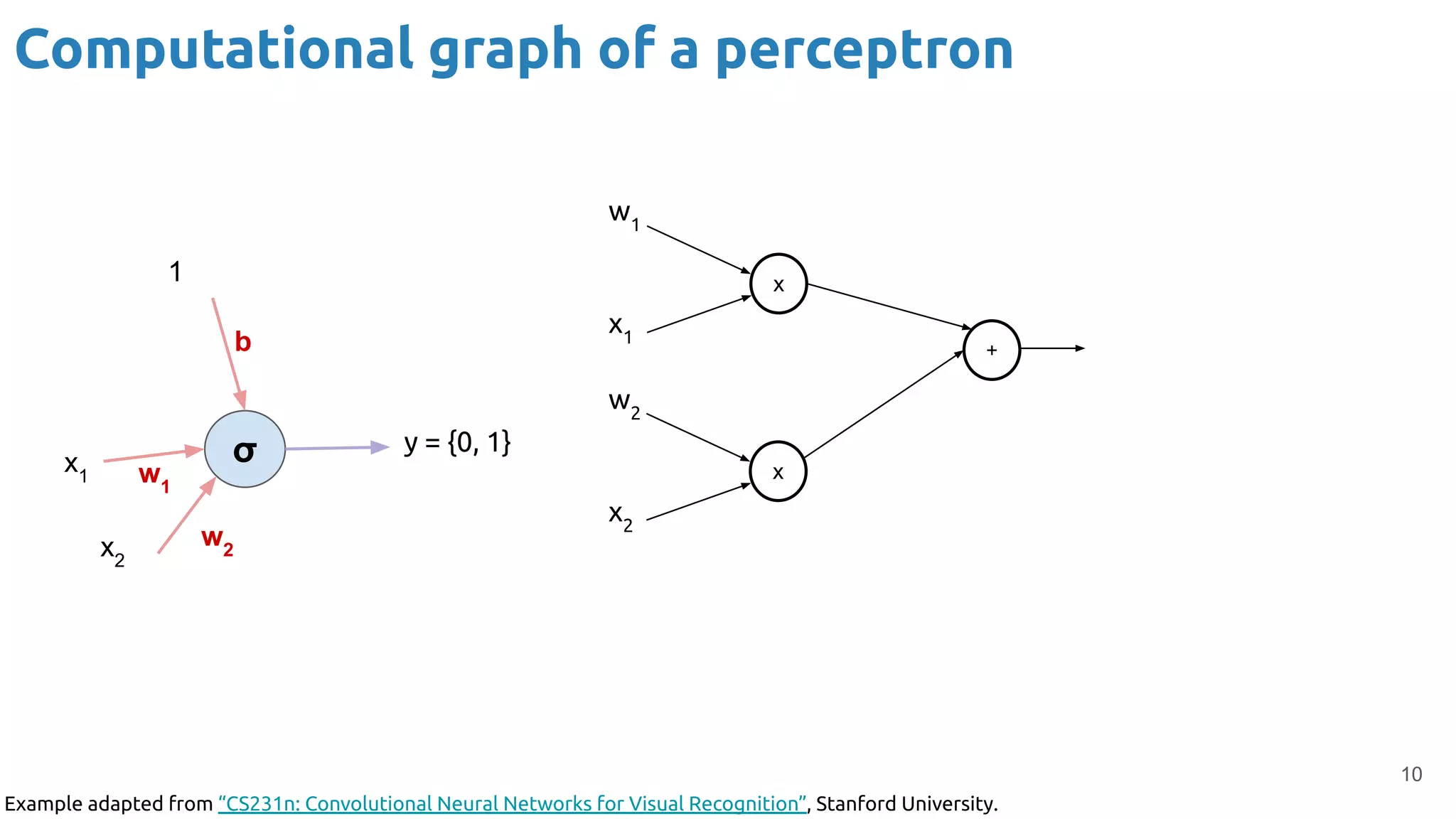
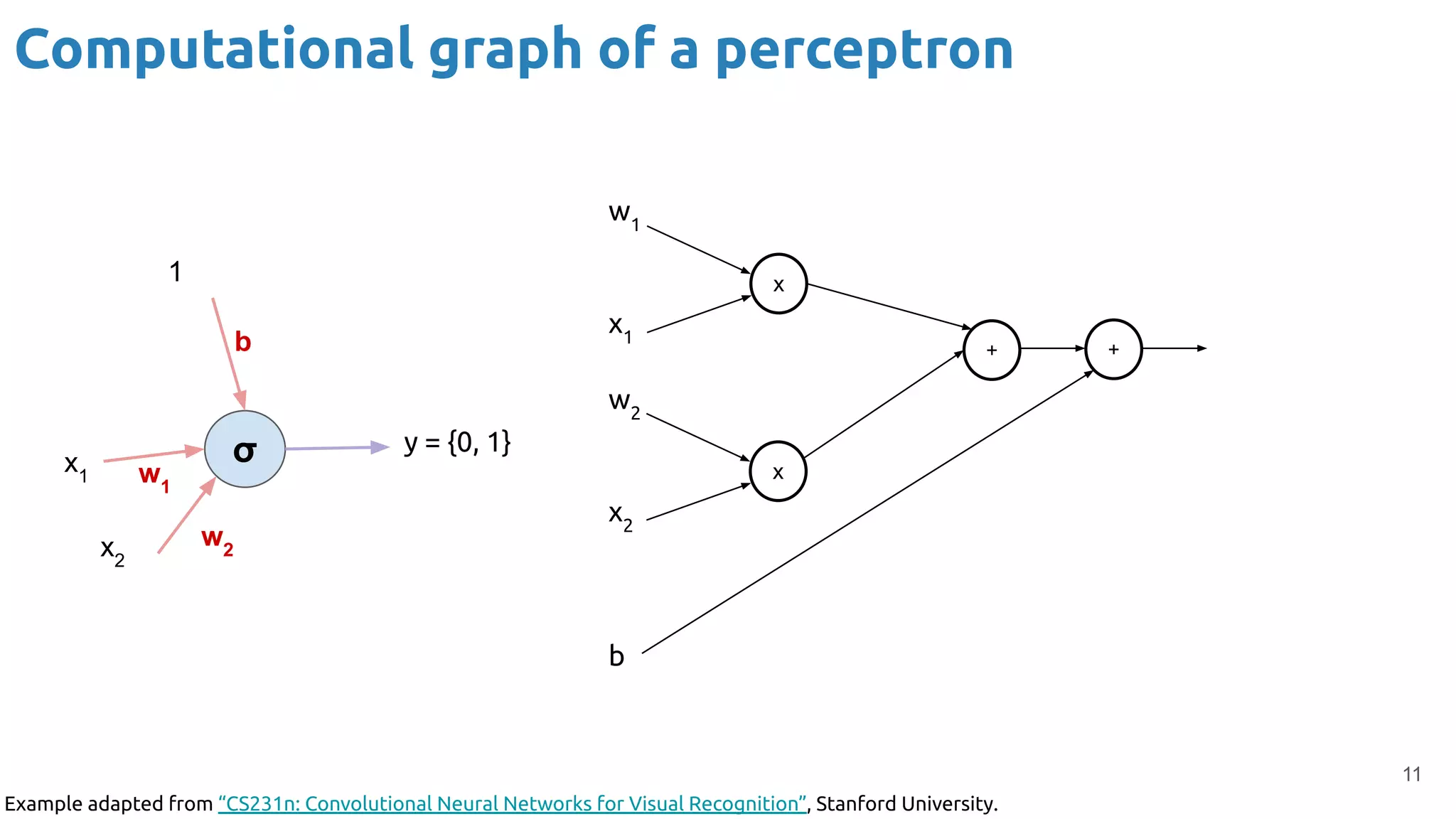
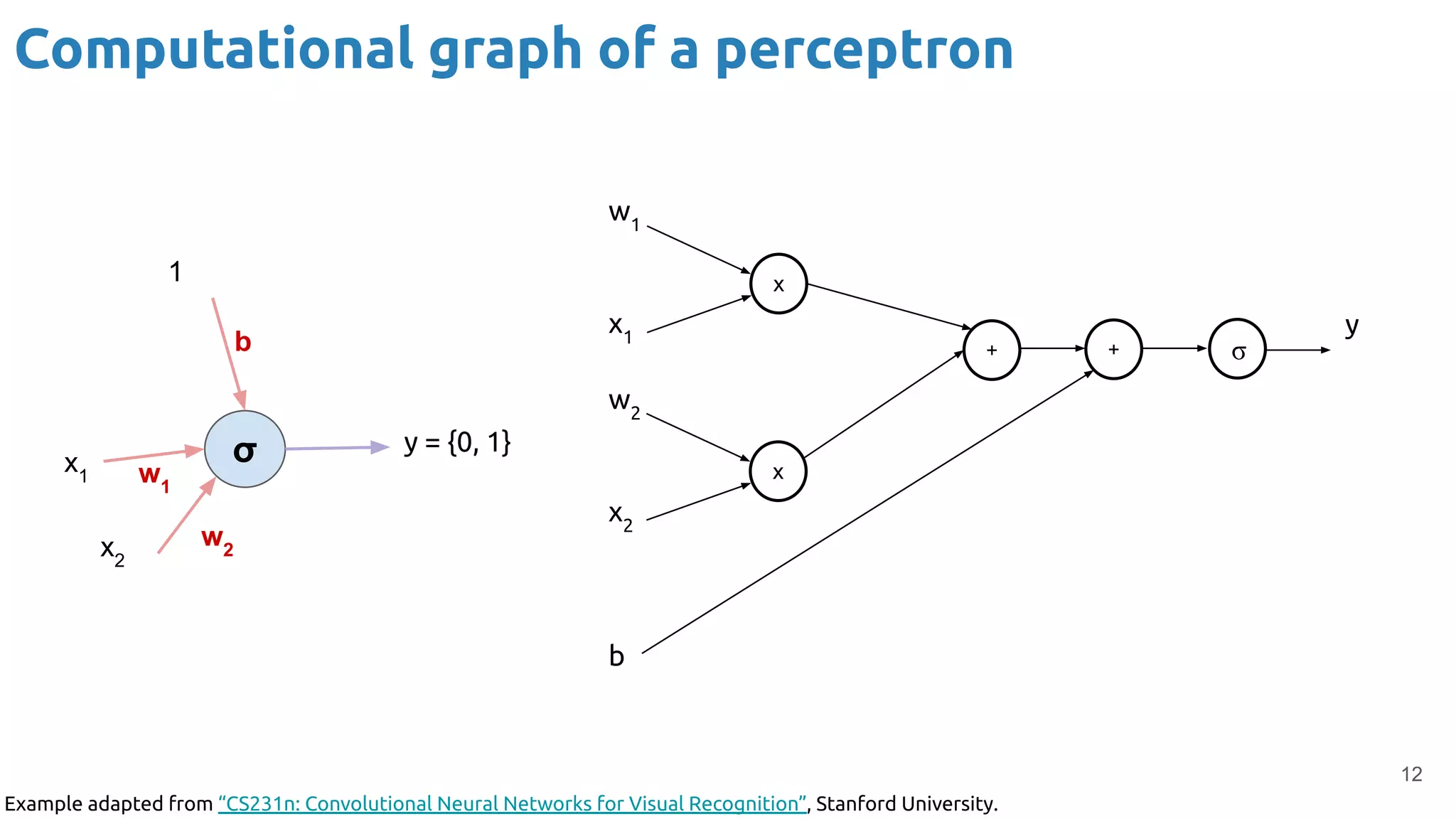
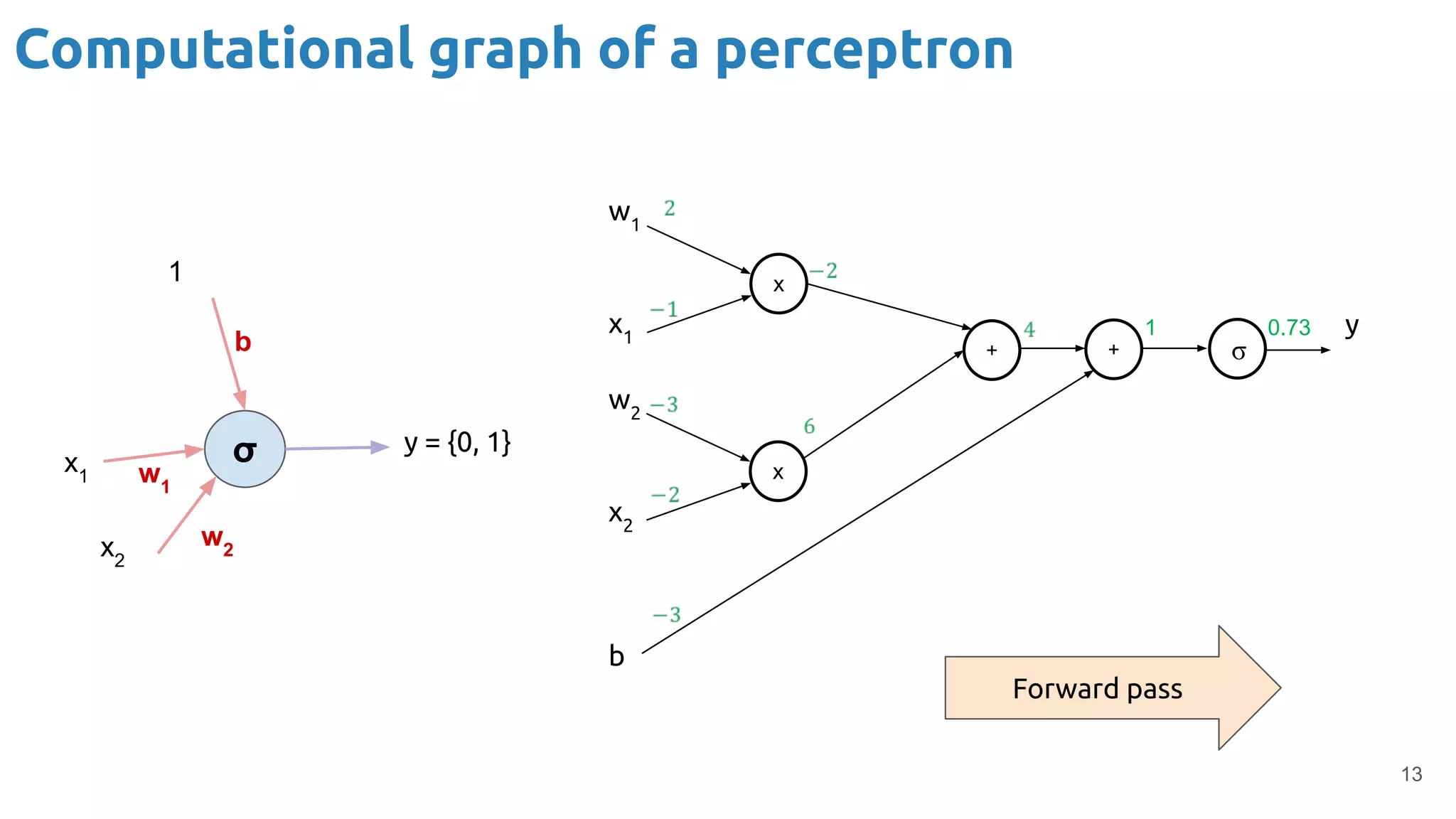
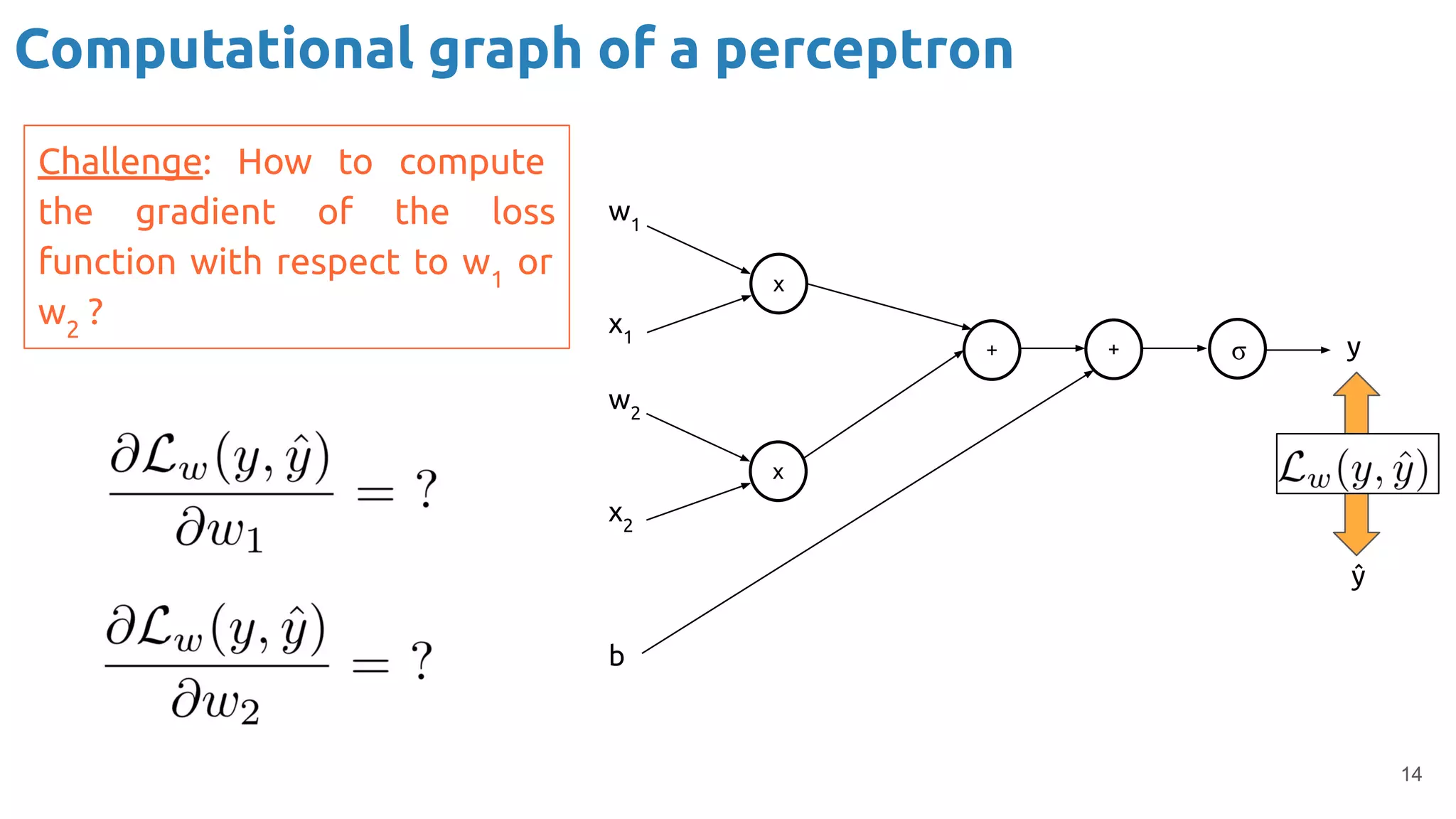
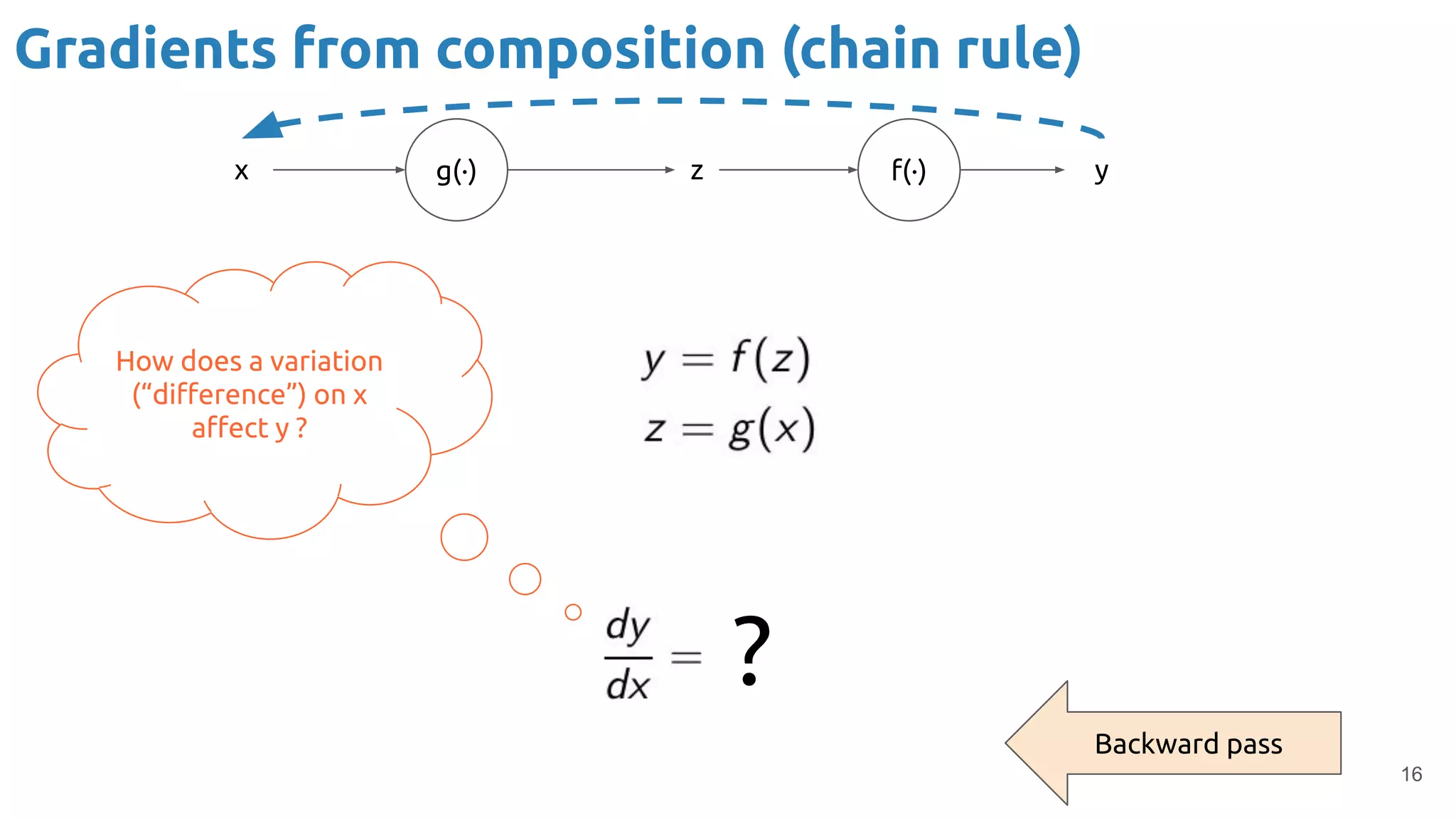
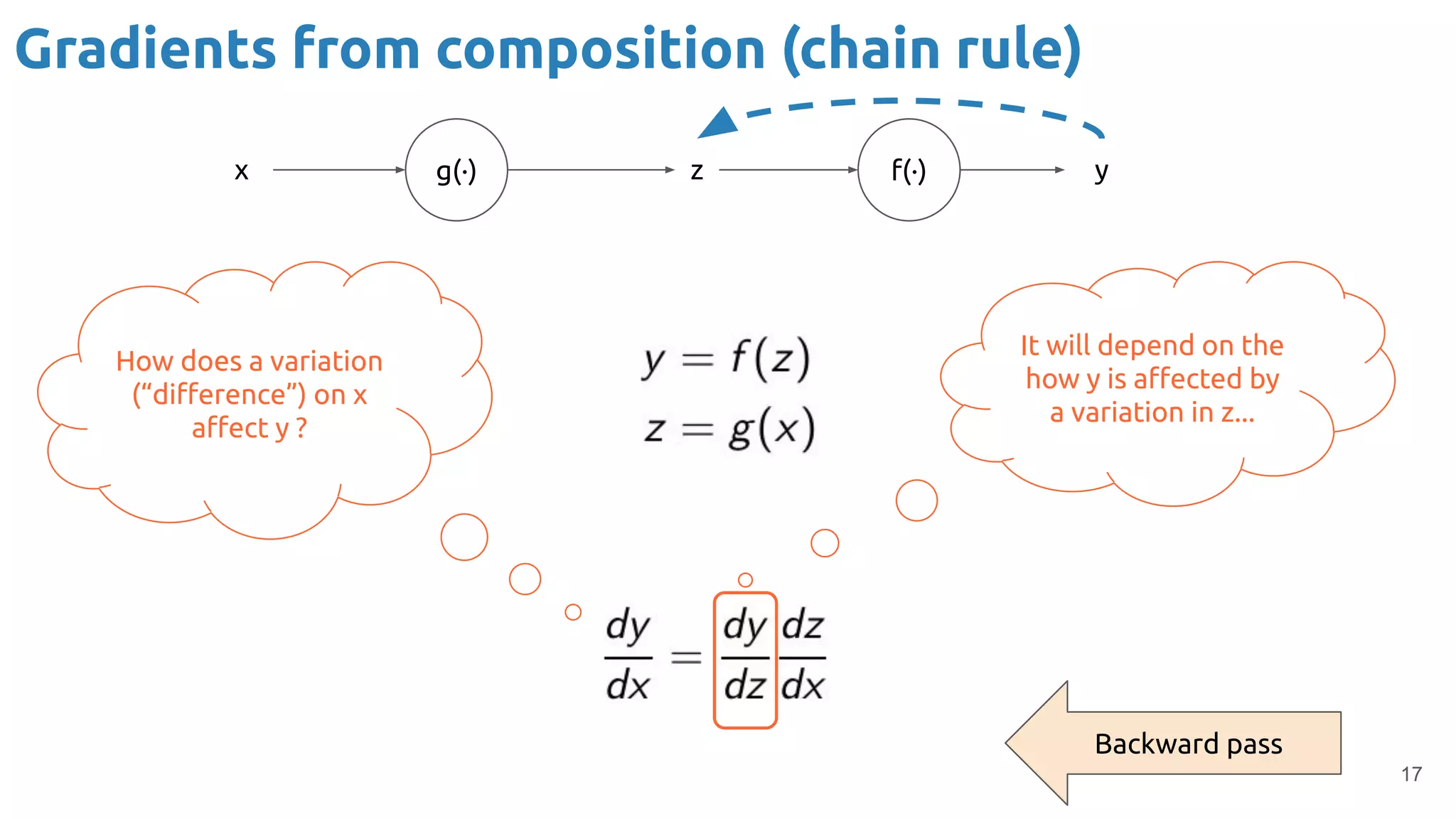
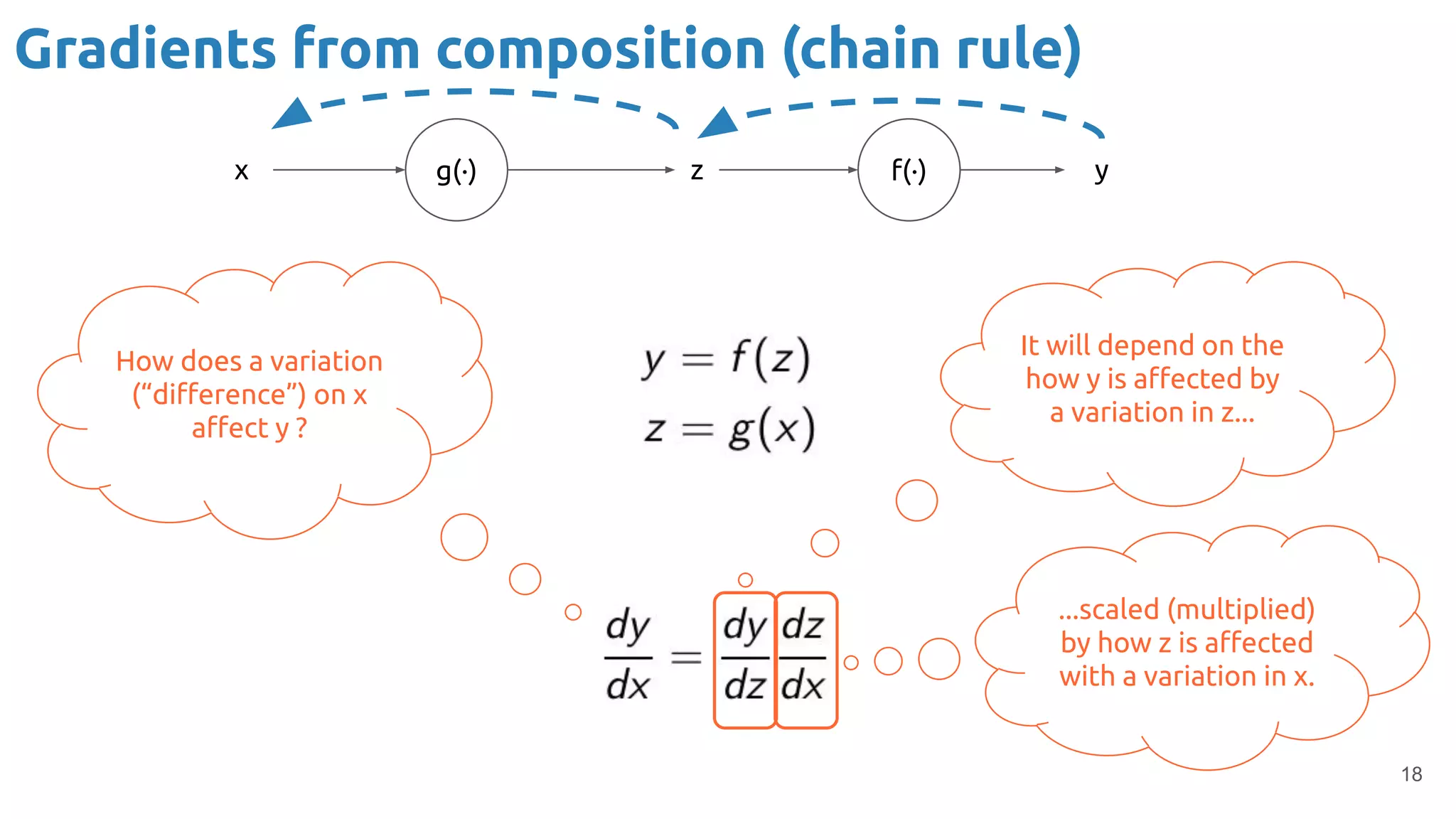
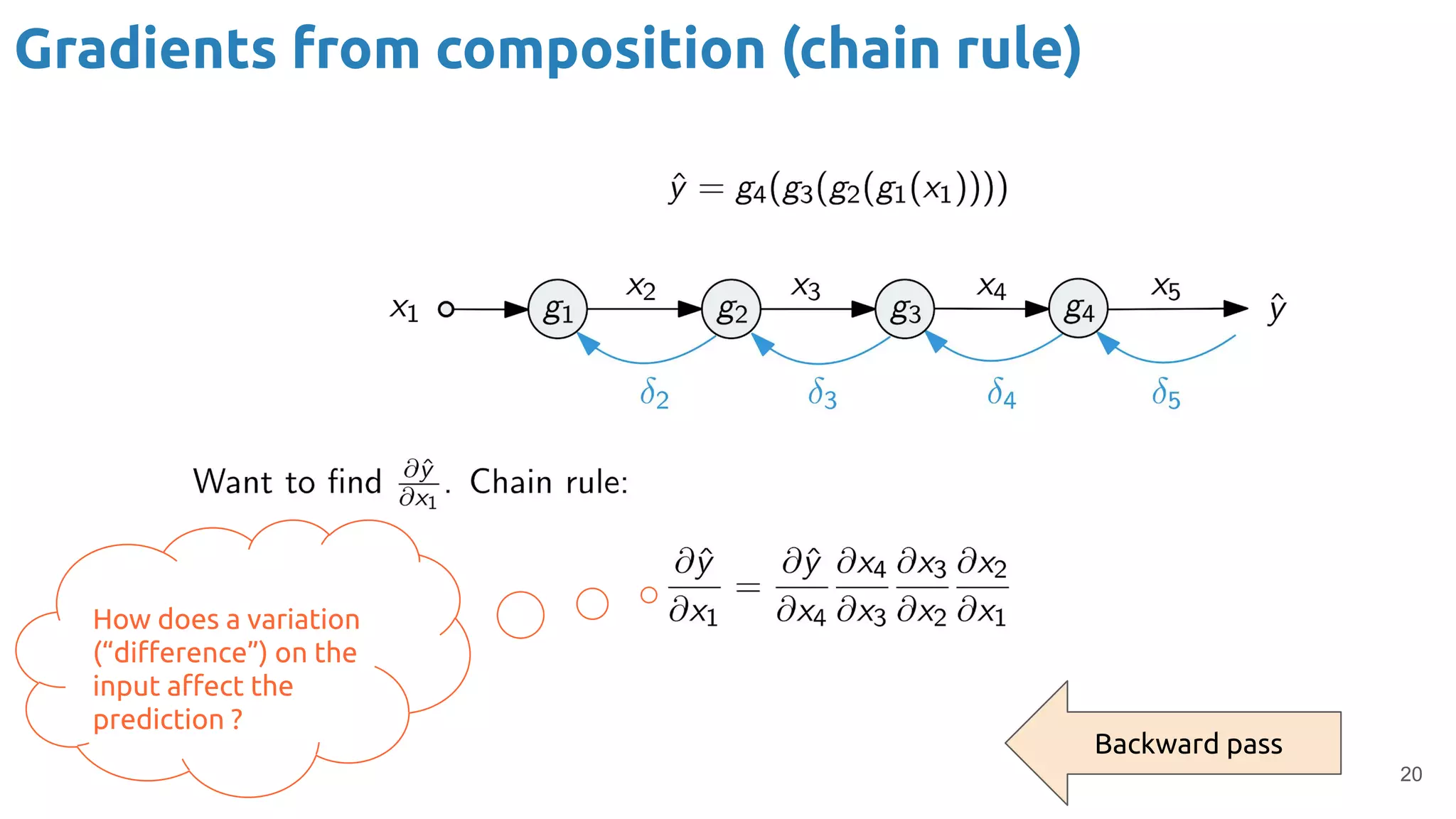
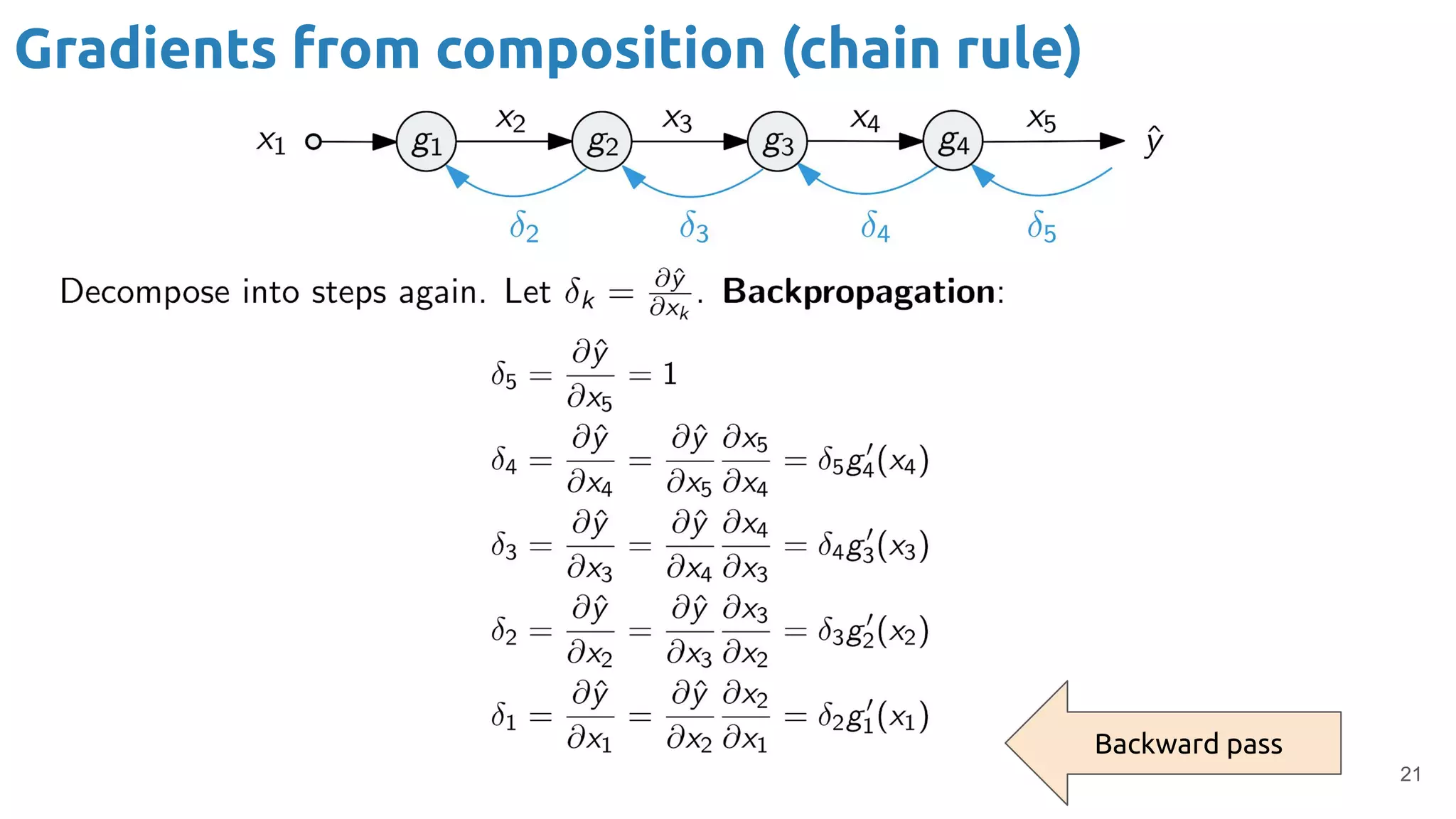
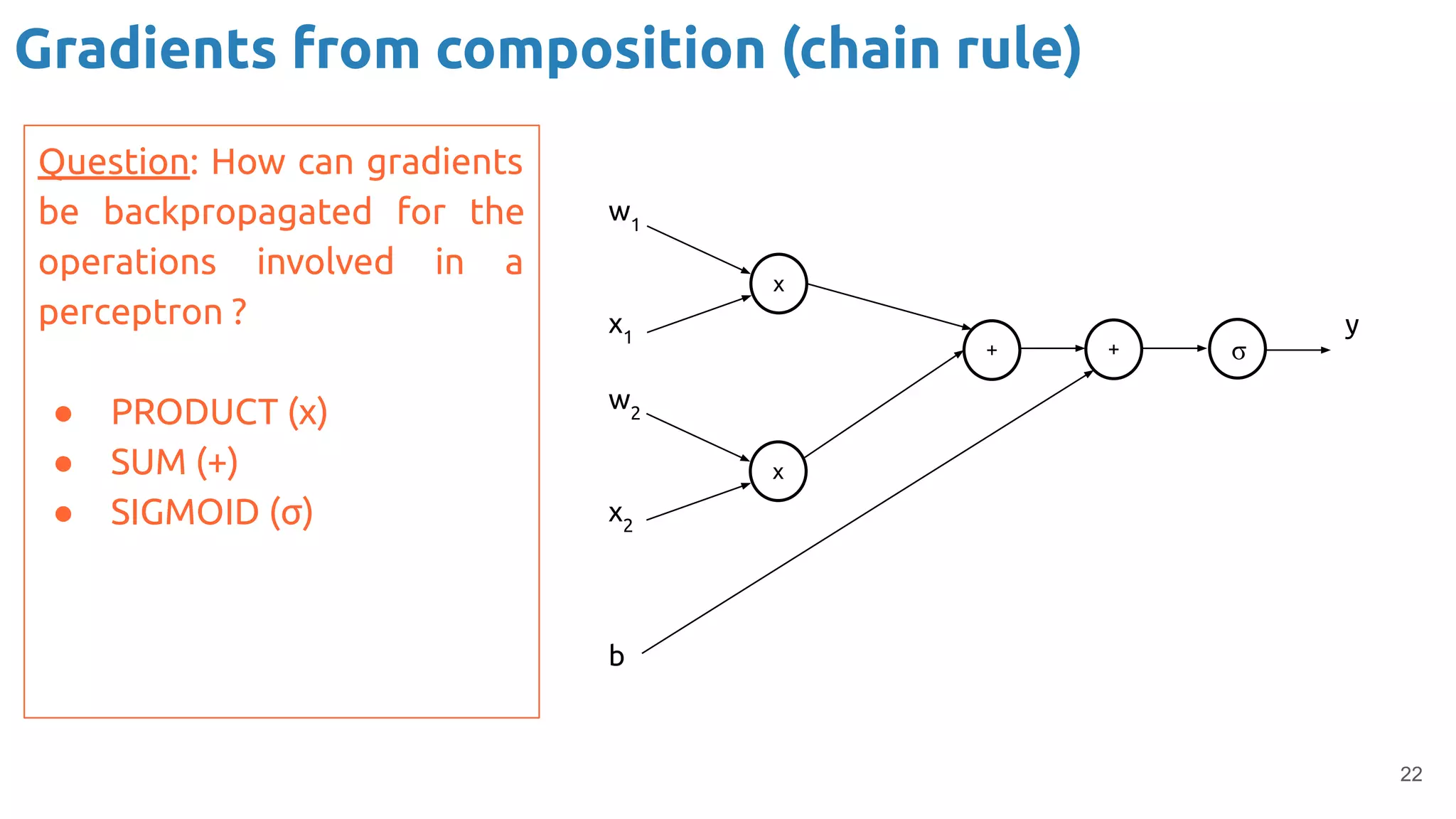
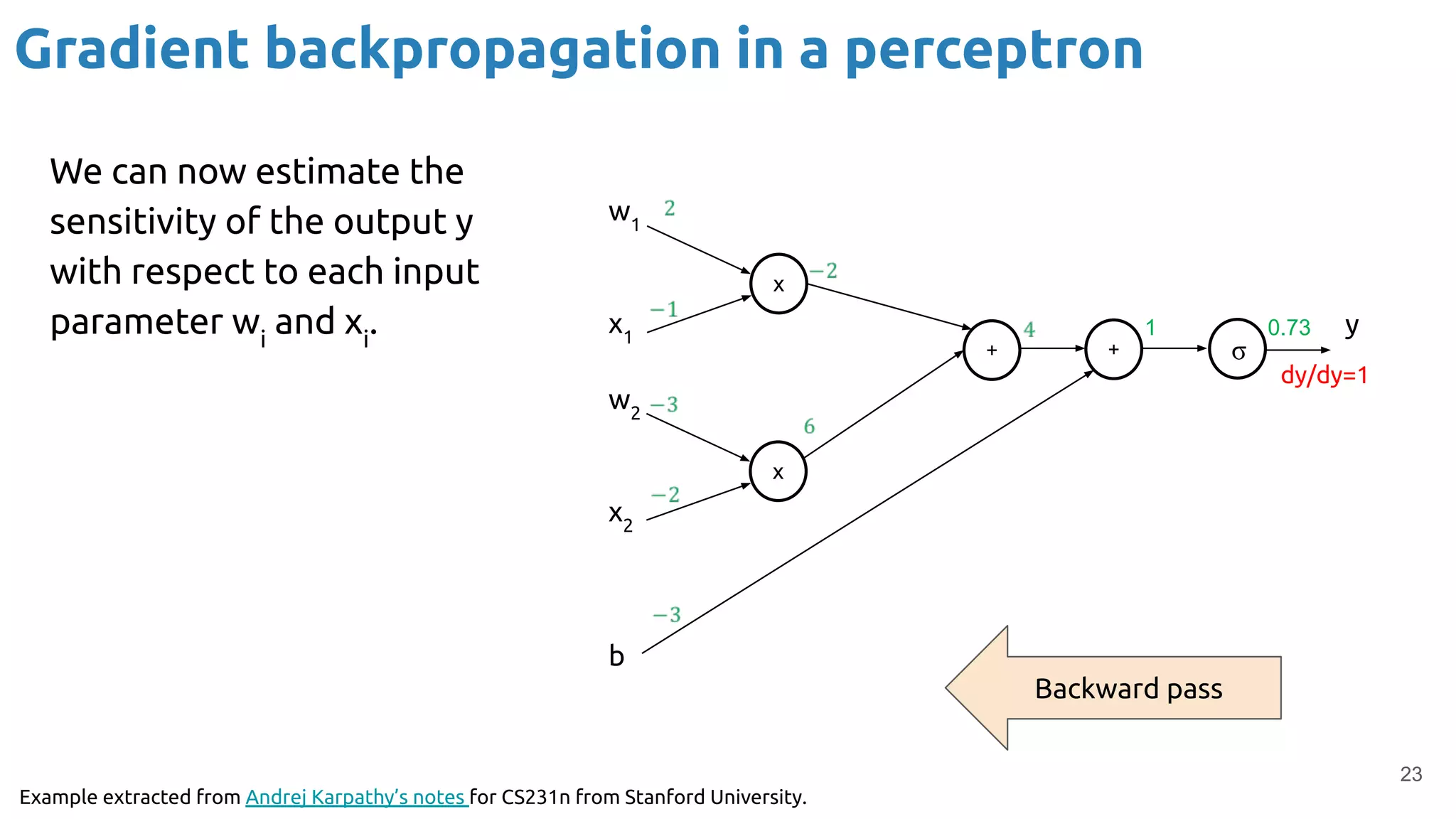
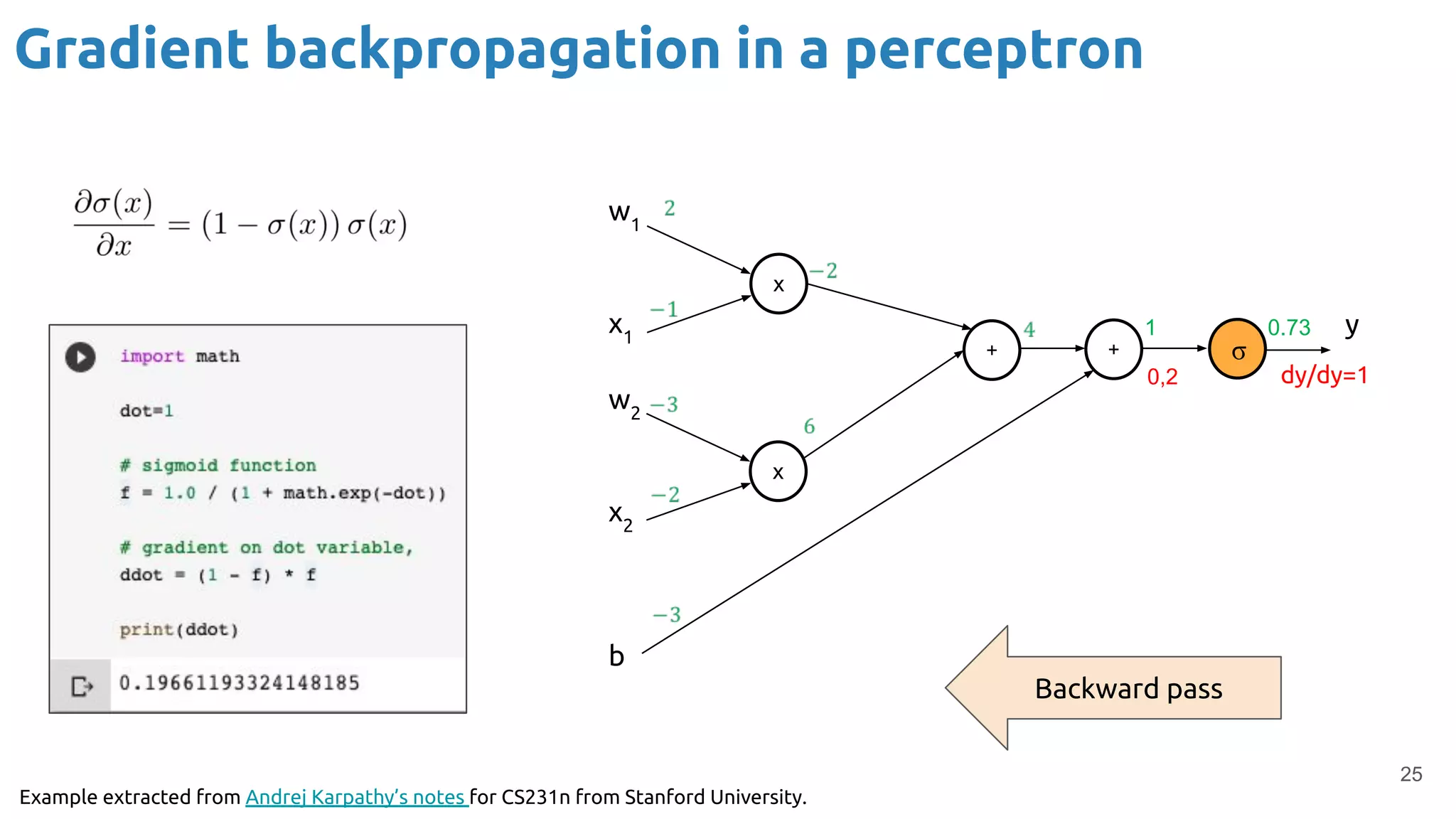
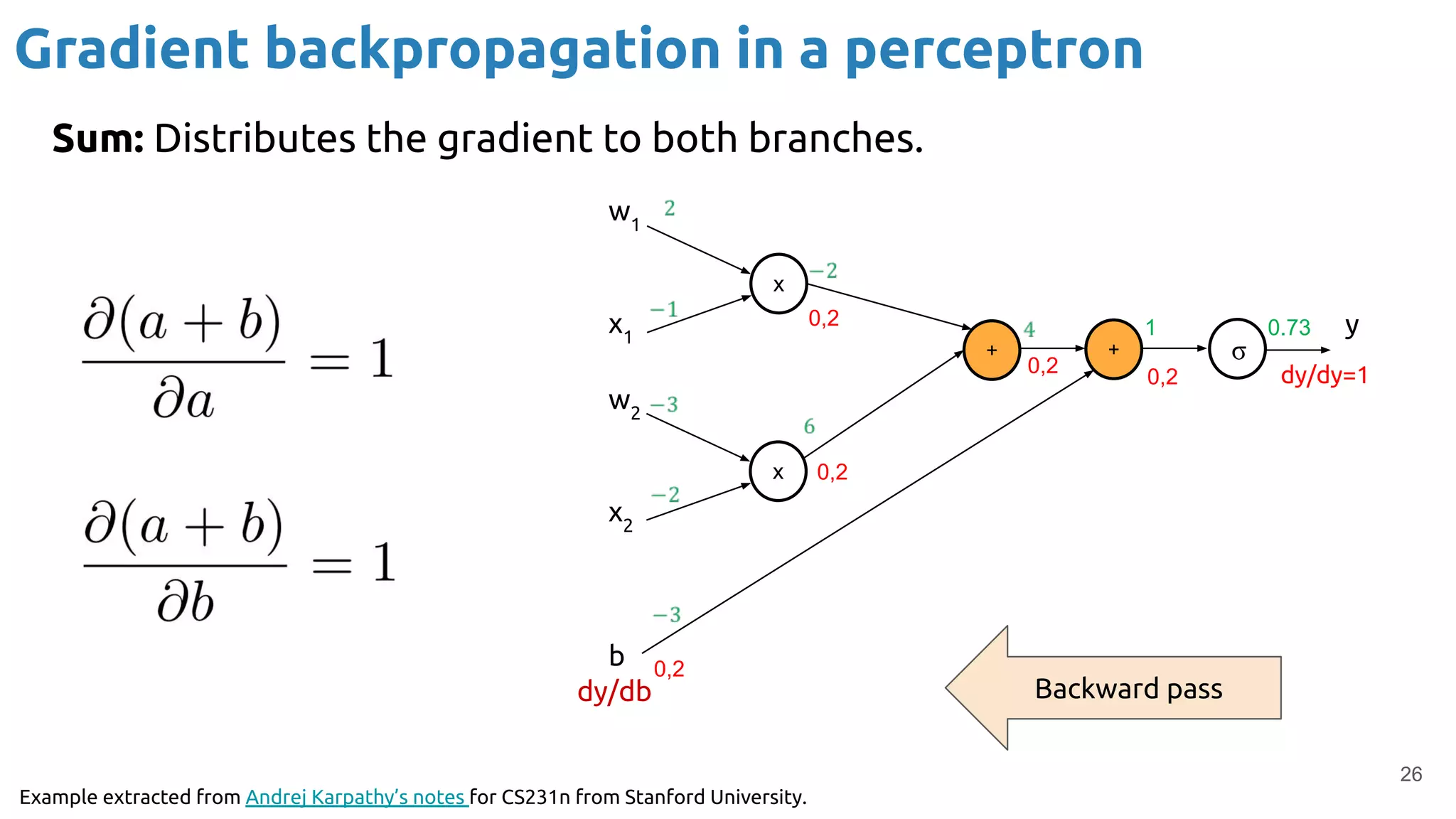
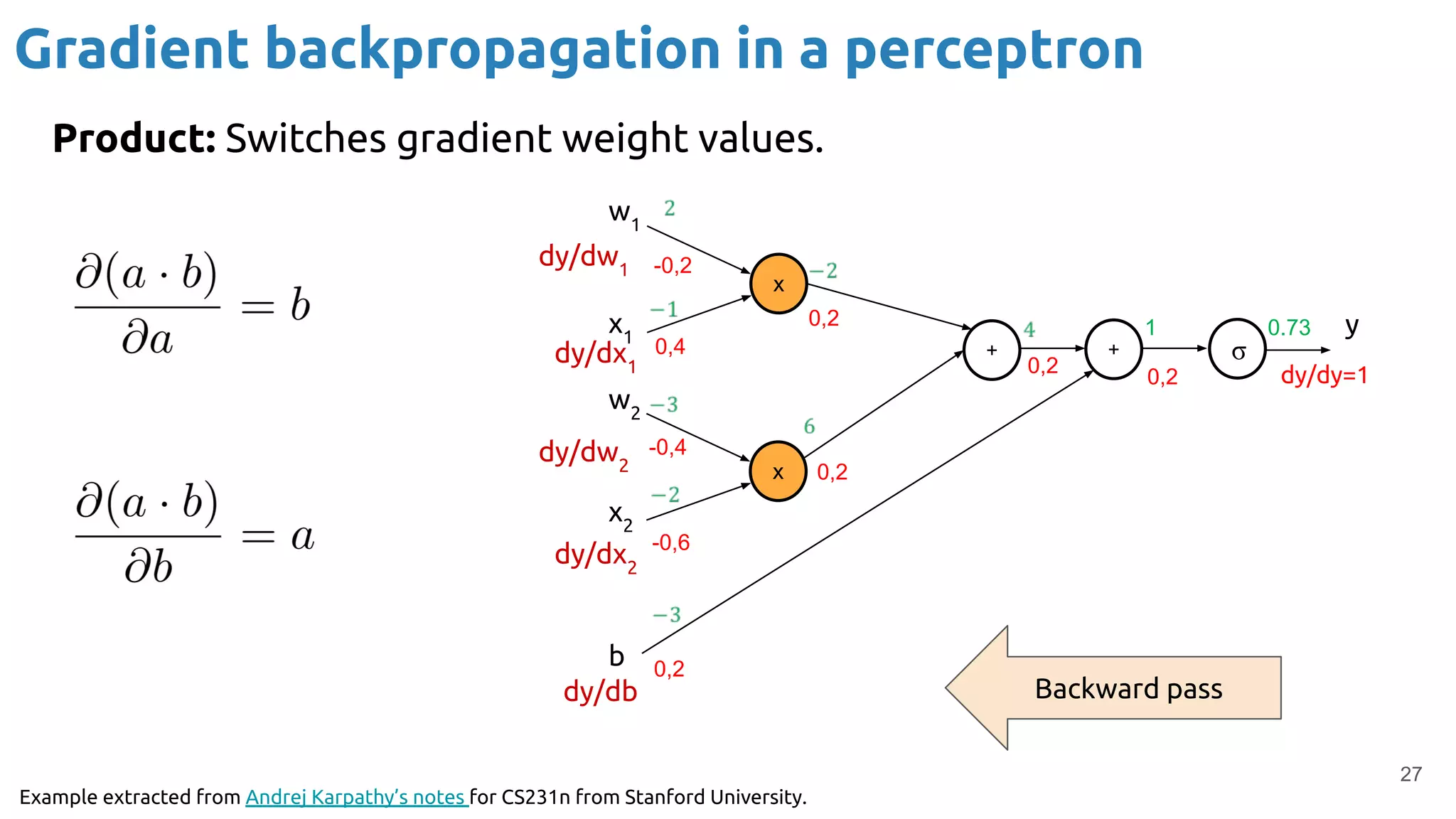
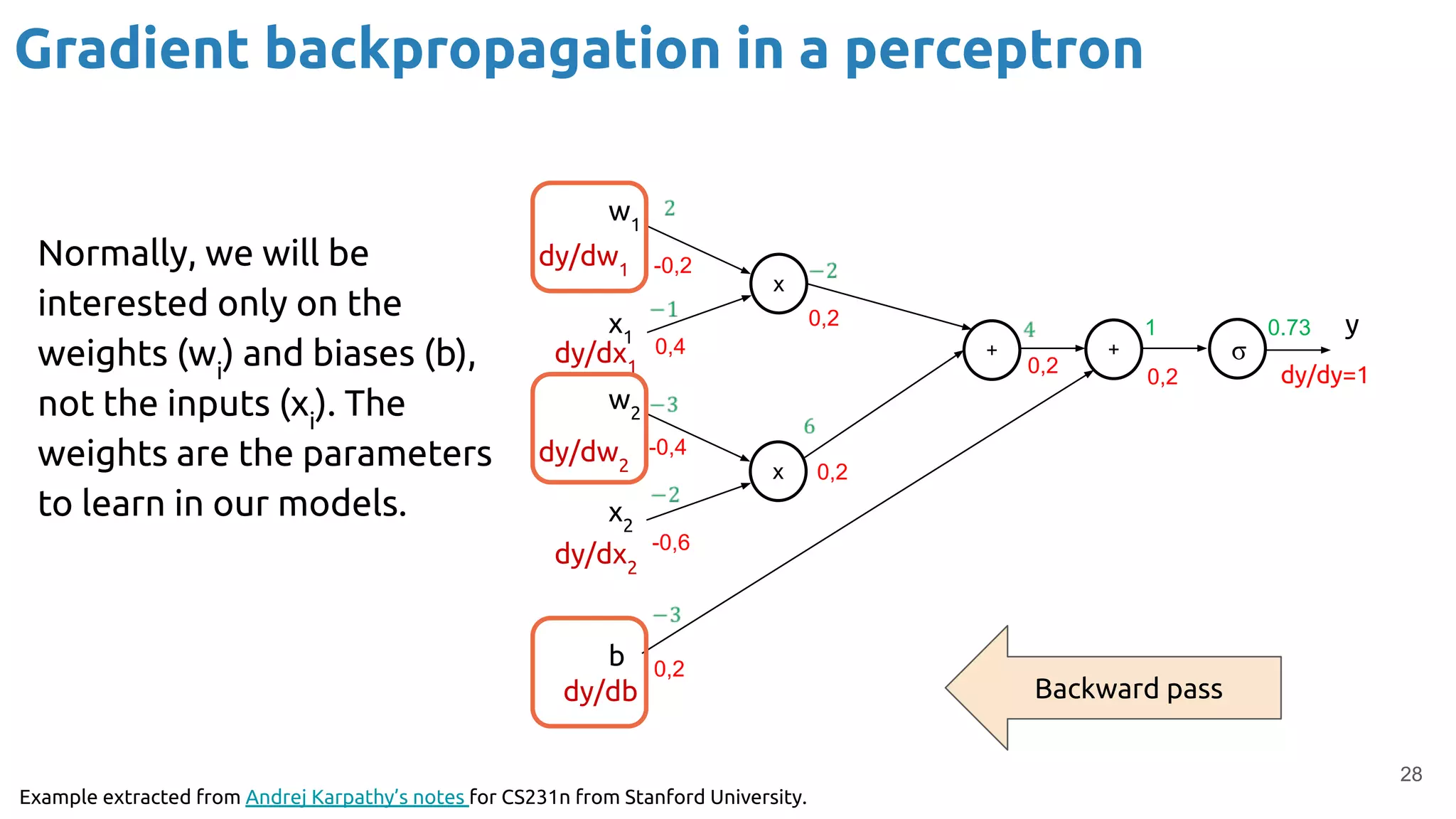
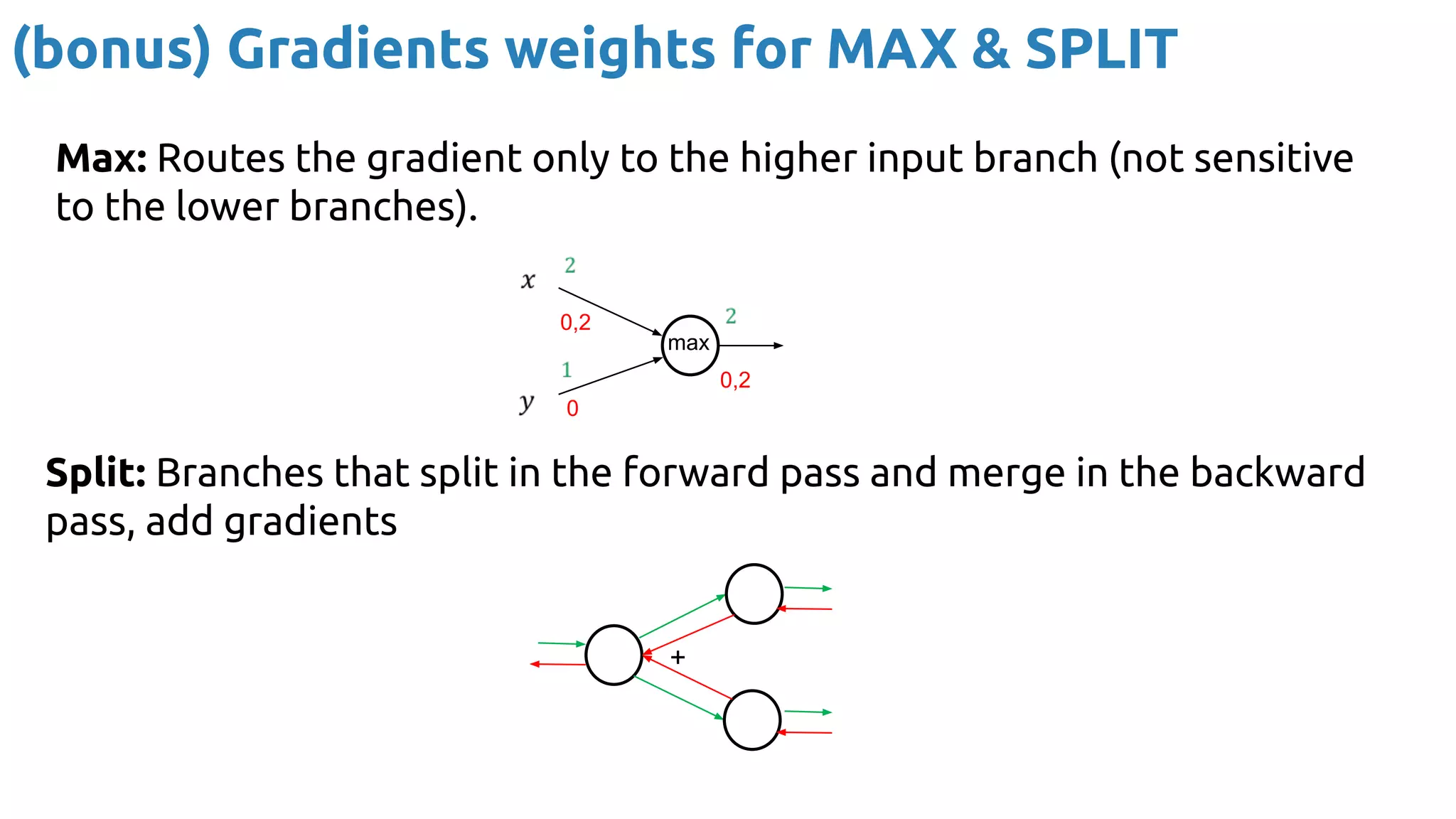
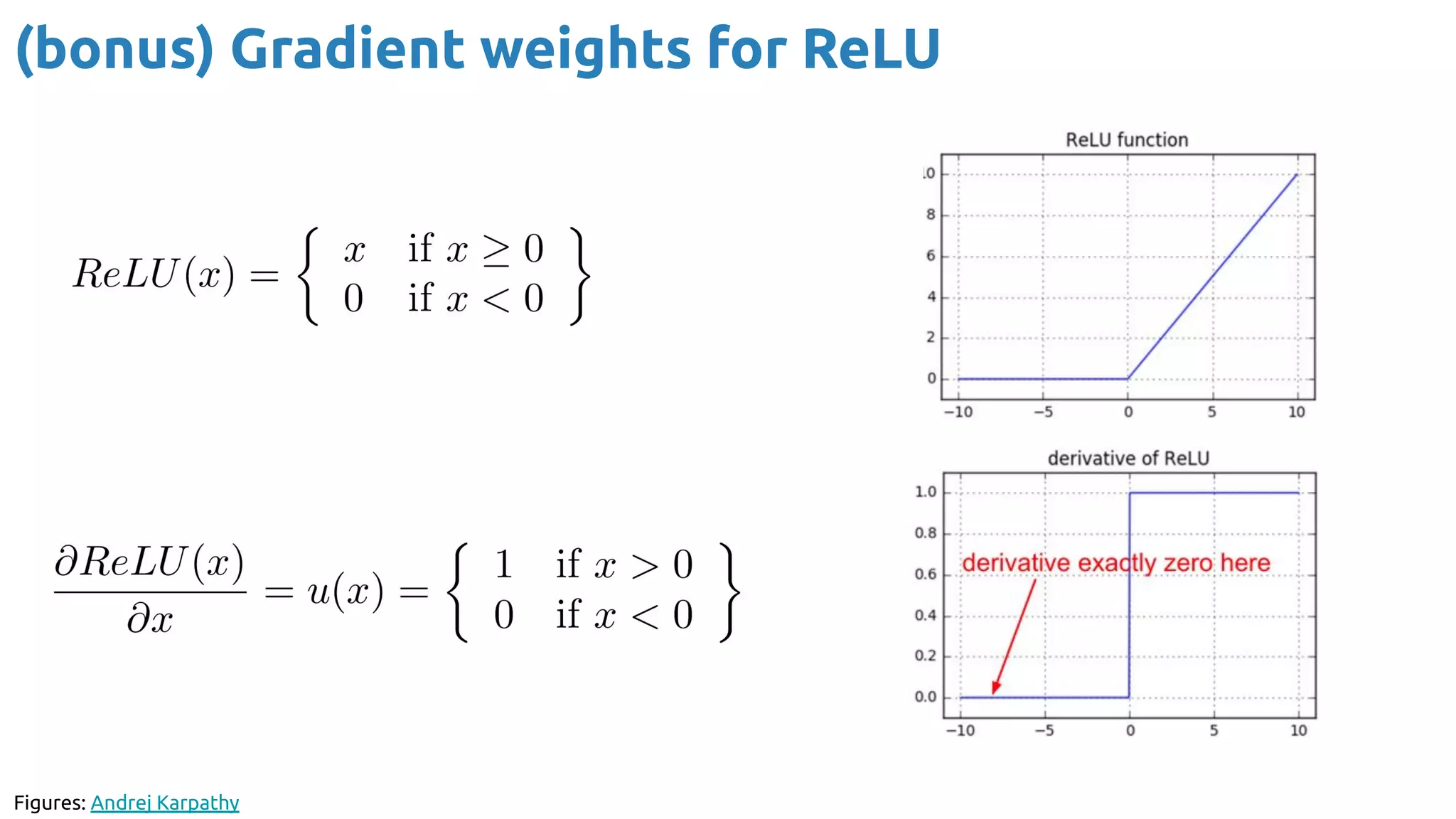
The document discusses the loss function and gradient descent in the context of neural networks, specifically focusing on backpropagation as a method to compute gradients that optimize model parameters. It includes explanations of computational graphs for perceptrons and the role of activation functions, along with derivations of how gradients are propagated through different operations. Additionally, it offers insights into learning rates and links to further resources for deeper understanding.

1. Xavier Giro-i-Nieto
xavier.giro@upc.edu
Associate Professor
Universitat Politècnica de Catalunya
Technical University of Catalonia
Backpropagation
#DLUPC
[course site]

2. 2
Acknowledgements
Kevin McGuinness
kevin.mcguinness@dcu.ie
Research Fellow
Insight Centre for Data Analytics
Dublin City University
Elisa Sayrol
elisa.sayrol@upc.edu
Associate Professor
ETSETB TelecomBCN
Universitat Politècnica de Catalunya

3. 3
Video lecture

4. Loss function - L(y, ŷ)
The loss function assesses the performance of our model by comparing its
predictions (y) to an expected value (ŷ), typically coming from ground truth
labels.
Example: the predicted price (y) and one actually paid
could be compared with the Euclidean distance (also
referred as L2 distance or Mean Square Error - MSE): 1
x1
x2
x3
y = {-∞, ∞}
b
w1
w2
w3

5. Discussion: Consider the very simple
model...
…....and that, given a pair (y, ŷ), we would
like to update the current wt
value to a
new wt+1
based on the loss function Lw
.
(a) Would you increase or decrease wt
?
(b) What operation could indicate which
way to go ?
(c) How much would you increase or
decrease wt
?
Loss function - L(y, ŷ)
Lw

6. Motivation for this lecture:
if we had a way to compute the
gradient of the loss with respect to
the parameter(s), we could use
gradient descent to optimize them.
6
Gradient Descent (GD)
Descend
(minus sign)
Learning
rate (LR)
Lw

7. Backpropagation will allow us to compute the gradients of the loss function
with respect to:
● all model parameters (w) - final goal during training
● input/intermediate data - visualization & interpretability purposes.
Gradients will “flow” from the output of the model towards the input (“back”).
Gradient Descent (GD)

8. Computational graph of a simple perceptron
8
σ
1
x1
x2
y = {0, 1}
b
w1
w2
Question: What is the computational graph
(operations & order) of this perceptron with a
sigmoid activation ?

9. Computational graph of a perceptron
9
σ
1
x1
x2
y = {0, 1}
b
w1
w2
x
x
w1
x1
w2
x2
Example adapted from “CS231n: Convolutional Neural Networks for Visual Recognition”, Stanford University.

10. 10
σ
1
x1
x2
y = {0, 1}
b
w1
w2
x
+
x
w1
x1
w2
x2
Example adapted from “CS231n: Convolutional Neural Networks for Visual Recognition”, Stanford University.
Computational graph of a perceptron

11. 11
σ
1
x1
x2
y = {0, 1}
b
w1
w2
x
+
x
+
w1
x1
w2
x2
b
Example adapted from “CS231n: Convolutional Neural Networks for Visual Recognition”, Stanford University.
Computational graph of a perceptron

12. 12
σ
1
x1
x2
y = {0, 1}
b
w1
w2
x
+
x
+ σ
w1
x1
w2
x2
b
Example adapted from “CS231n: Convolutional Neural Networks for Visual Recognition”, Stanford University.
y
Computational graph of a perceptron

13. 13
σ
1
x1
x2
y = {0, 1}
b
w1
w2
x
+
x
+ σ
1 0.73
Computational graph of a perceptron
y
Forward pass
w1
x1
w2
x2
b

14. 14
x
+
x
+ σ
Challenge: How to compute
the gradient of the loss
function with respect to w1
or
w2
?
w1
x1
w2
x2
b
y
ŷ
Computational graph of a perceptron

15. 15
Gradients from composition (chain rule)
f(·)g(·) zx y
Forward pass

16. 16
How does a variation
(“difference”) on x
affect y ?
?
Gradients from composition (chain rule)
f(·)g(·) zx y
Backward pass

17. 17
How does a variation
(“difference”) on x
affect y ?
It will depend on the
how y is affected by
a variation in z...
Gradients from composition (chain rule)
f(·)g(·) zx y
Backward pass

18. 18
How does a variation
(“difference”) on x
affect y ?
It will depend on the
how y is affected by
a variation in z...
...scaled (multiplied)
by how z is affected
with a variation in x.
Gradients from composition (chain rule)
f(·)g(·) zx y

19. 19
Gradients from composition (chain rule)
Forward pass

20. 20
Gradients from composition (chain rule)
How does a variation
(“difference”) on the
input affect the
prediction ?
Backward pass

21. 21
Gradients from composition (chain rule)
Backward pass

22. 22
Gradients from composition (chain rule)
x
+
x
+ σ
y
w1
x1
w2
x2
b
Question: How can gradients
be backpropagated for the
operations involved in a
perceptron ?
● PRODUCT (x)
● SUM (+)
● SIGMOID (σ)

23. 23
Gradient backpropagation in a perceptron
We can now estimate the
sensitivity of the output y
with respect to each input
parameter wi
and xi
.
Example extracted from Andrej Karpathy’s notes for CS231n from Stanford University.
w1
x1
w2
x2
b
x
+
x
+ σ
1 0.73 y
dy/dy=1
Backward pass

24. Gradient weights for sigmoid σ
Even more details: Arunava, “Derivative of the Sigmoid function” (2018)
x
+
x
+ σ
y
w1
x1
w2
x2
b
...which can be re-arranged as...
(*)
(*)
Figure: Andrej Karpathy

25. 25
Gradient backpropagation in a perceptron
w1
x1
w2
x2
b
x
+
x
+ σ
1 0.73
0,2
y
dy/dy=1
Example extracted from Andrej Karpathy’s notes for CS231n from Stanford University.
Backward pass

26. 26
Sum: Distributes the gradient to both branches.
w1
x1
w2
x2
b
x
+
x
+ σ
1 0.73
0,2
0,2
0,2
0,2
y
dy/dy=1
Gradient backpropagation in a perceptron
Example extracted from Andrej Karpathy’s notes for CS231n from Stanford University.
Backward passdy/db
0,2

27. 27
x
+
x
+ σ
1 0.73
0,2
0,2
0,2
-0,2
0,2
0,2
0,4
-0,4
-0,6
y
dy/dy=1
Product: Switches gradient weight values.
Gradient backpropagation in a perceptron
Example extracted from Andrej Karpathy’s notes for CS231n from Stanford University.
Backward pass
w1
x1
w2
x2
b
dy/dw1
dy/dx1
dy/dw2
dy/dx2
dy/db

28. 28
w1
x1
w2
x2
b
x
+
x
+ σ
1 0.73
0,2
0,2
0,2
-0,2
0,2
0,2
0,4
-0,4
-0,6
y
dy/dy=1
Gradient backpropagation in a perceptron
Example extracted from Andrej Karpathy’s notes for CS231n from Stanford University.
Normally, we will be
interested only on the
weights (wi
) and biases (b),
not the inputs (xi
). The
weights are the parameters
to learn in our models.
Backward pass
dy/dw1
dy/dx1
dy/dw2
dy/dx2
dy/db

29. (bonus) Gradients weights for MAX & SPLIT
0,2
0,2
0
max
Max: Routes the gradient only to the higher input branch (not sensitive
to the lower branches).
Split: Branches that split in the forward pass and merge in the backward
pass, add gradients
+

30. (bonus) Gradient weights for ReLU
Figures: Andrej Karpathy

31. Learn more
31
READ
● Chris Olah, “Calculus on Computational Graphs: Backpropagation” (2015).
● Andrej Karpathy,, “Yes, you should understand backprop” (2016), and his “course notes at
Stanford University CS231n.
WATCH
● Gilbert Strang, “27. Backpropagation: Find Partial Derivatives”. MIT 18.065 (2018)