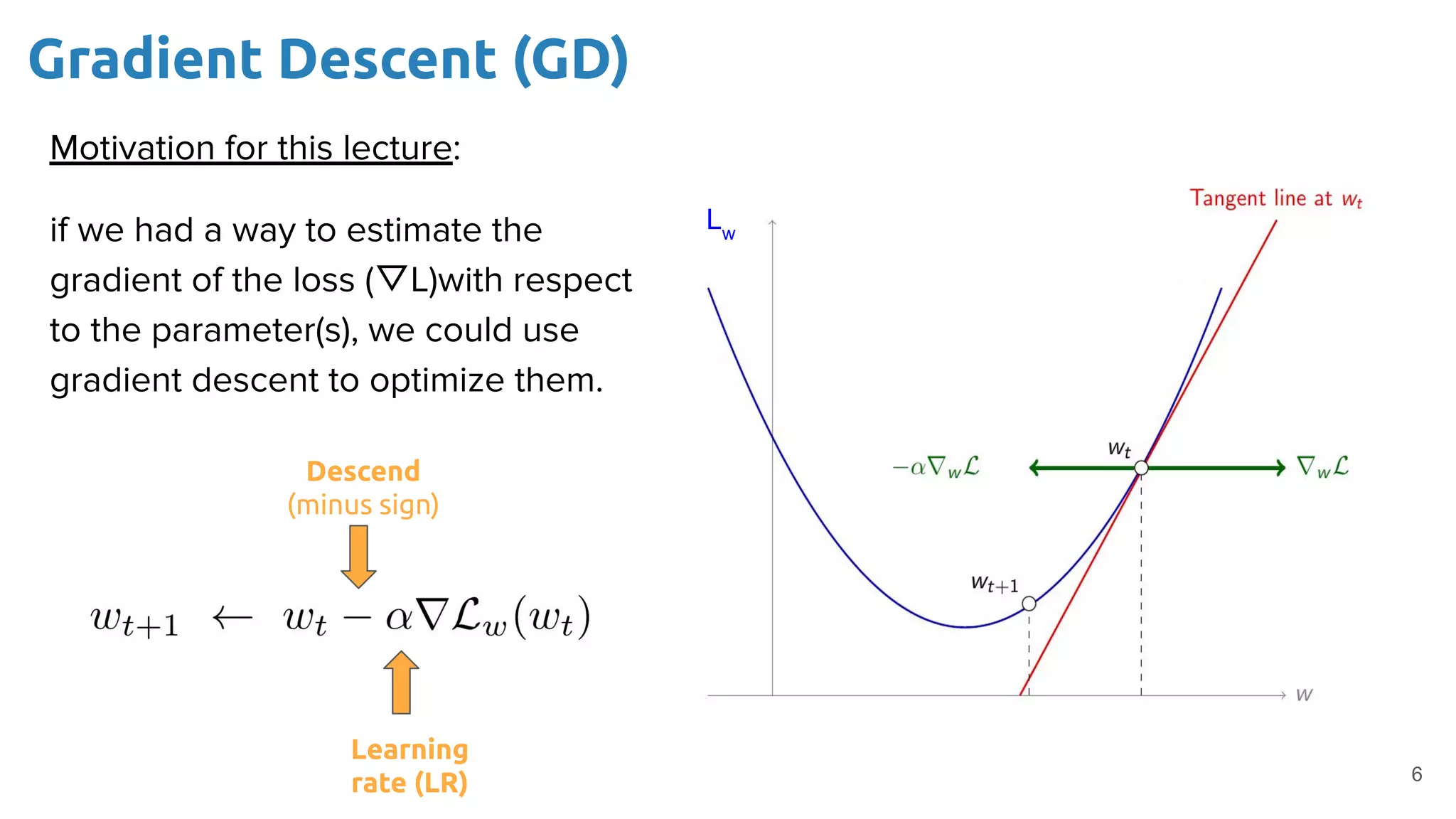
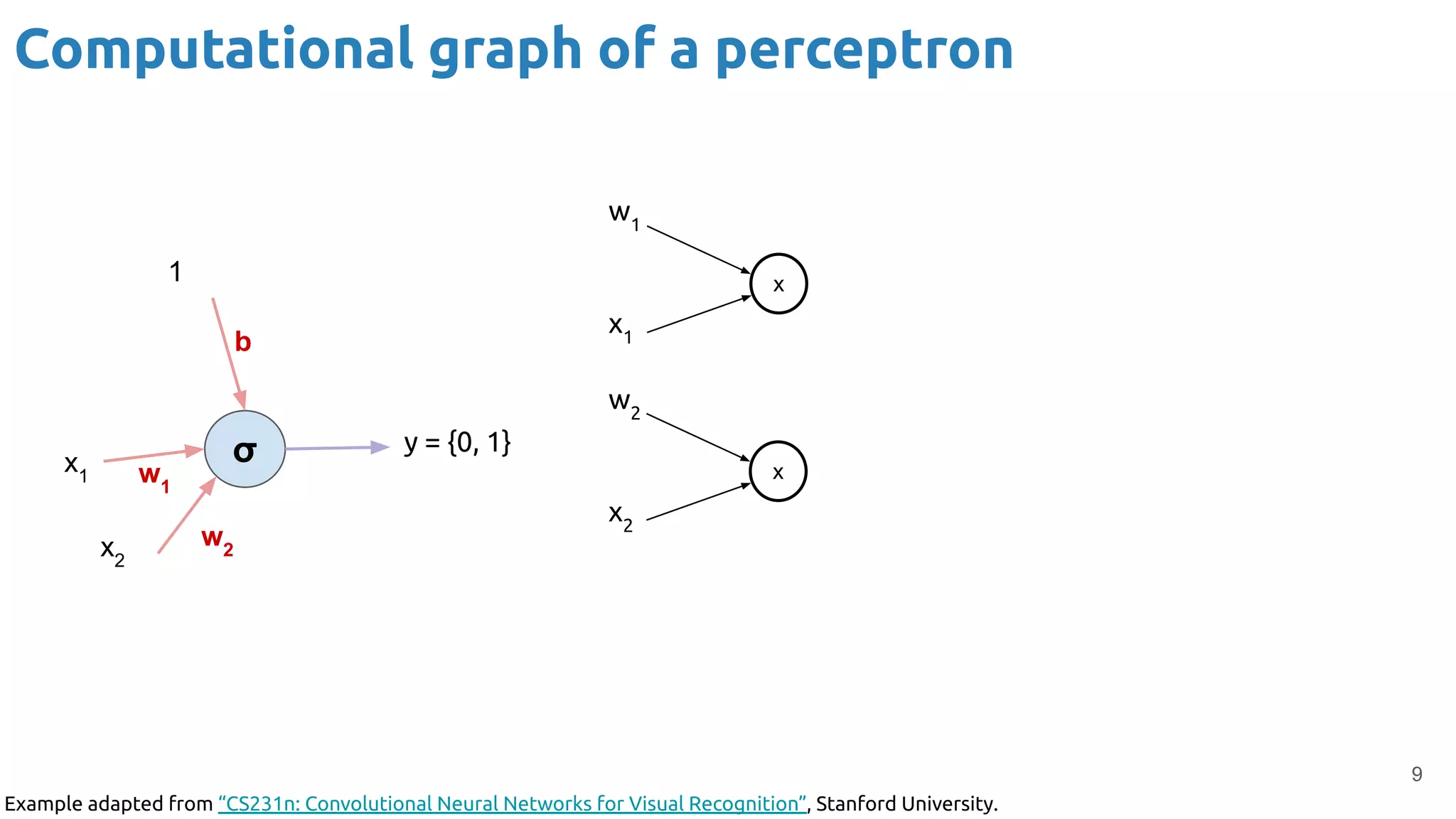
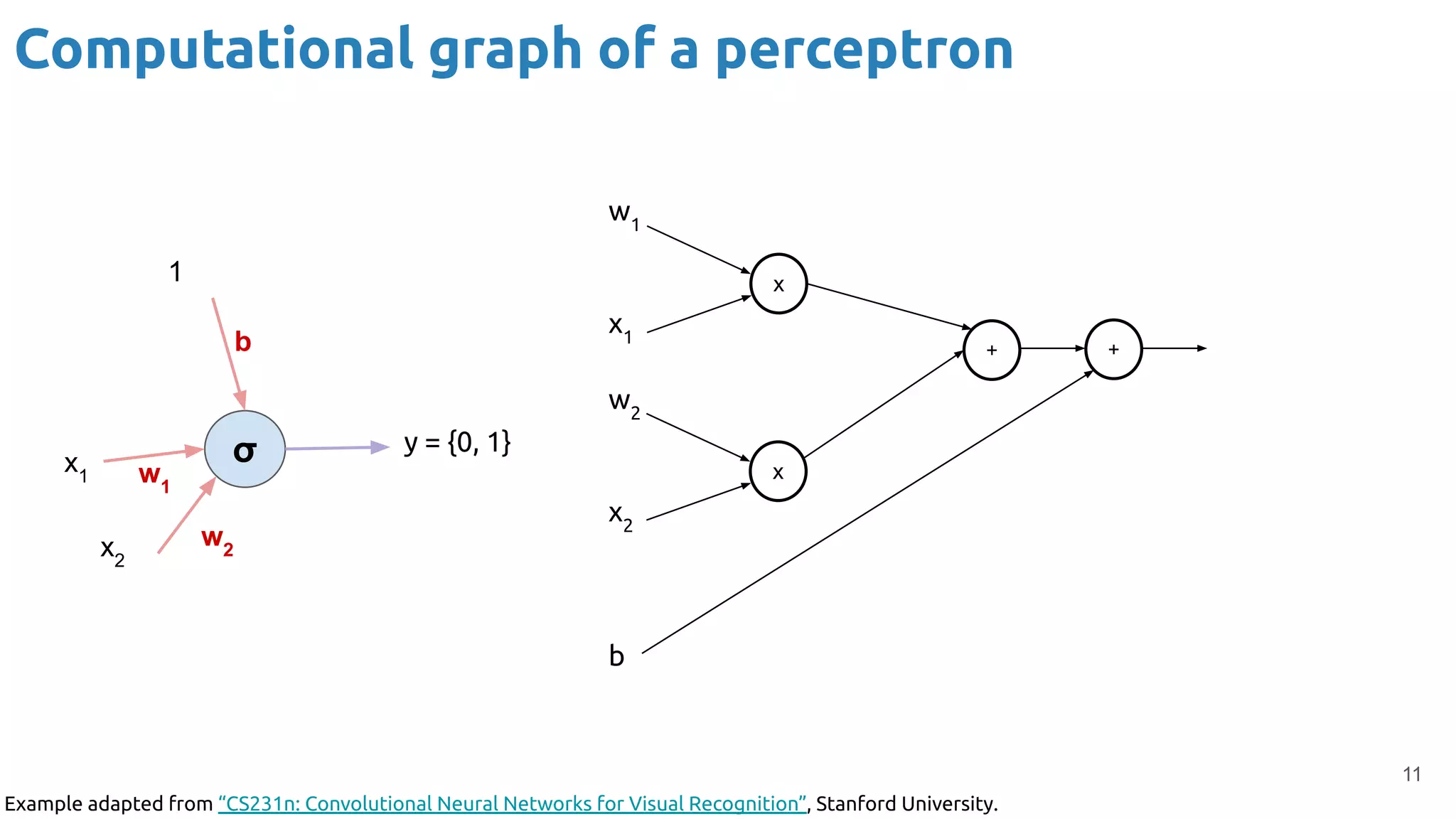
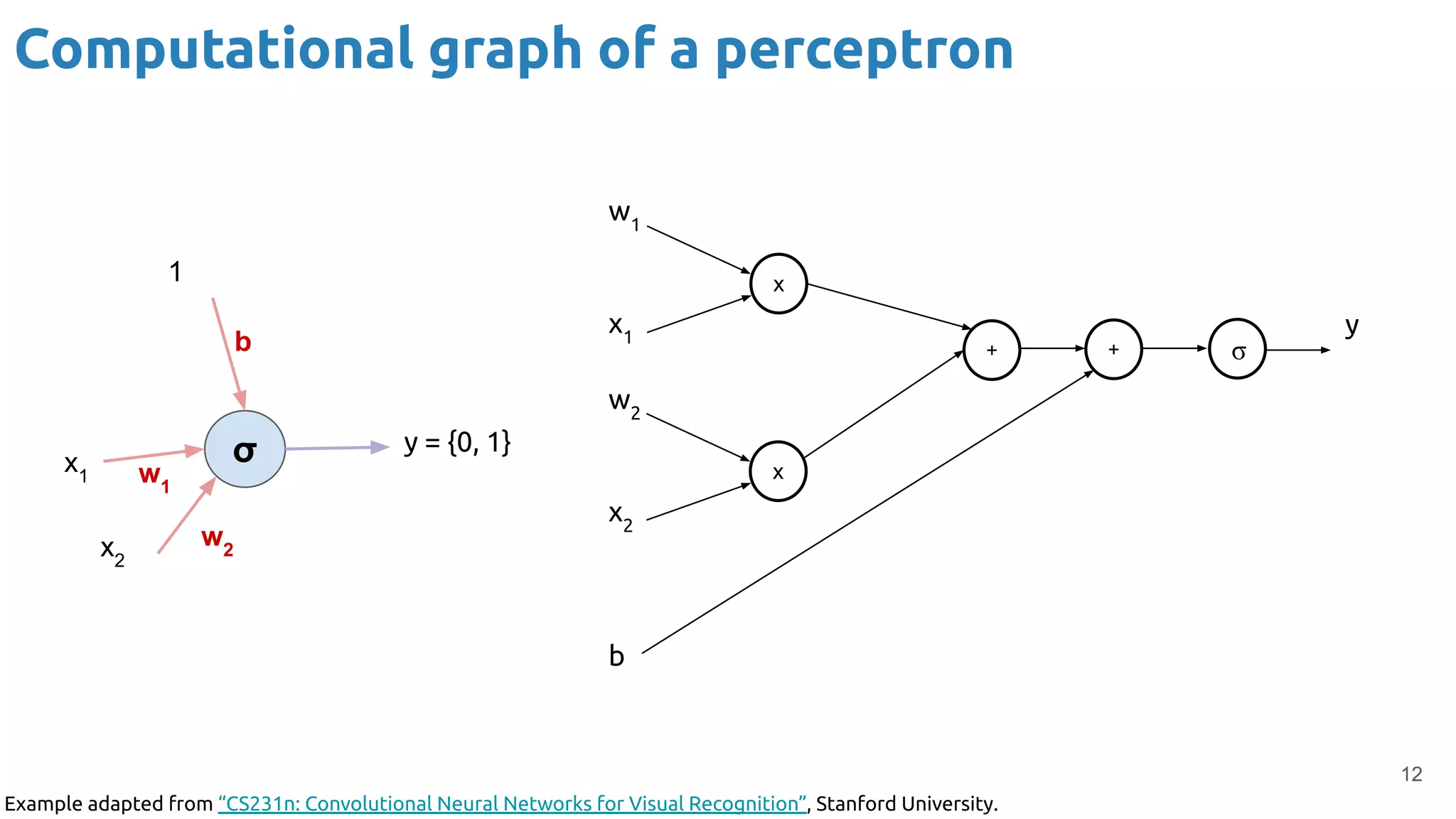
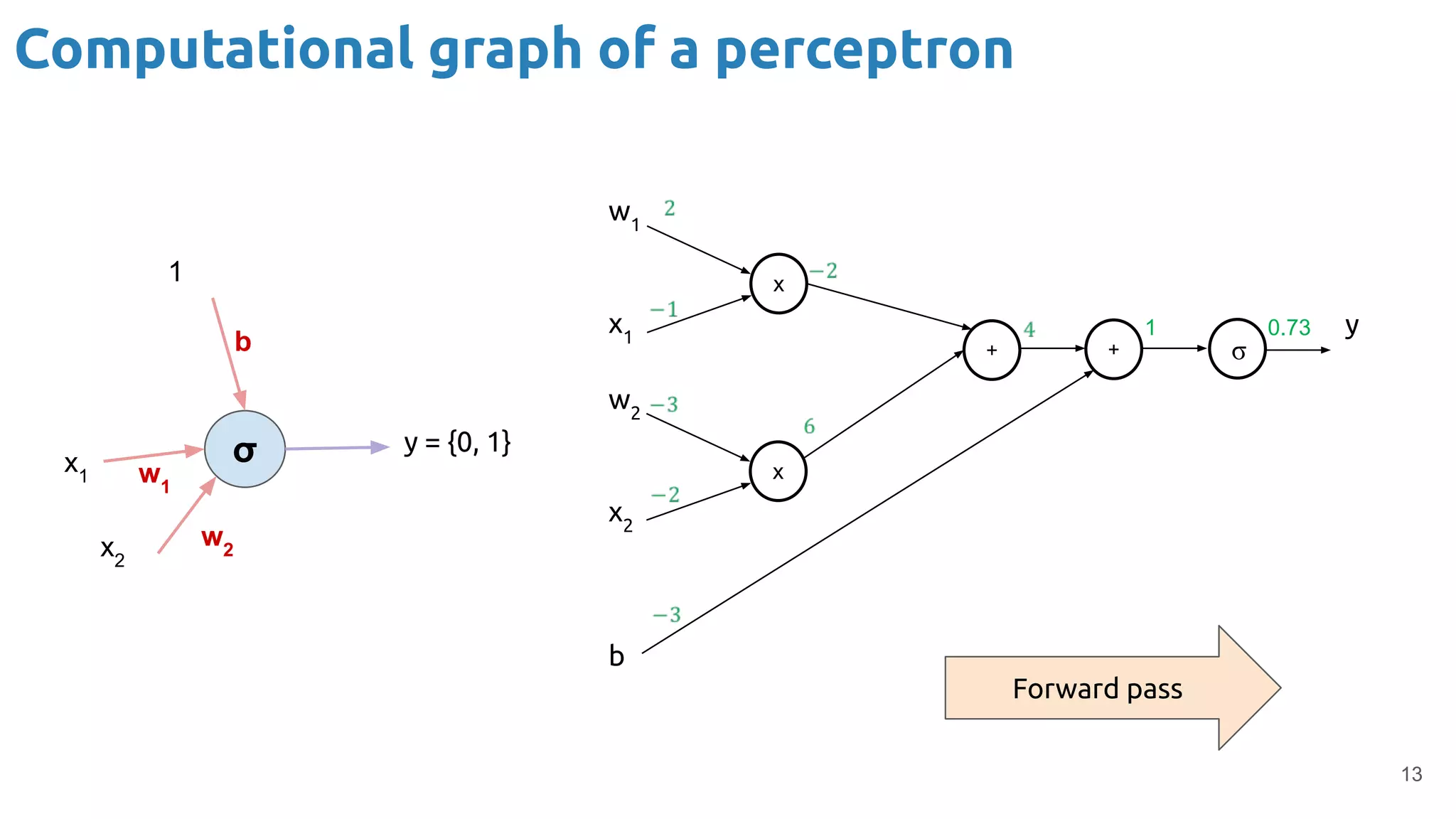
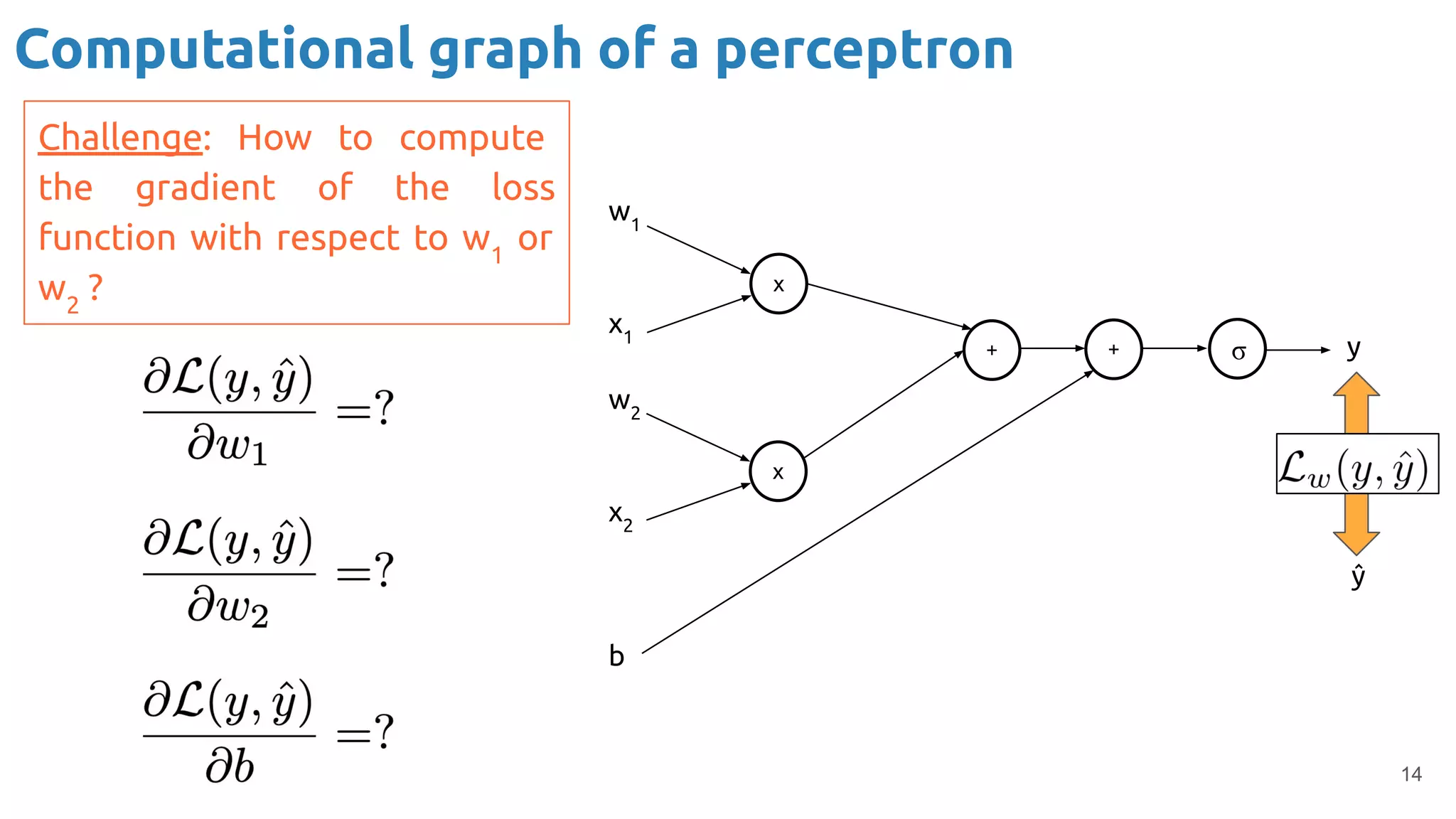
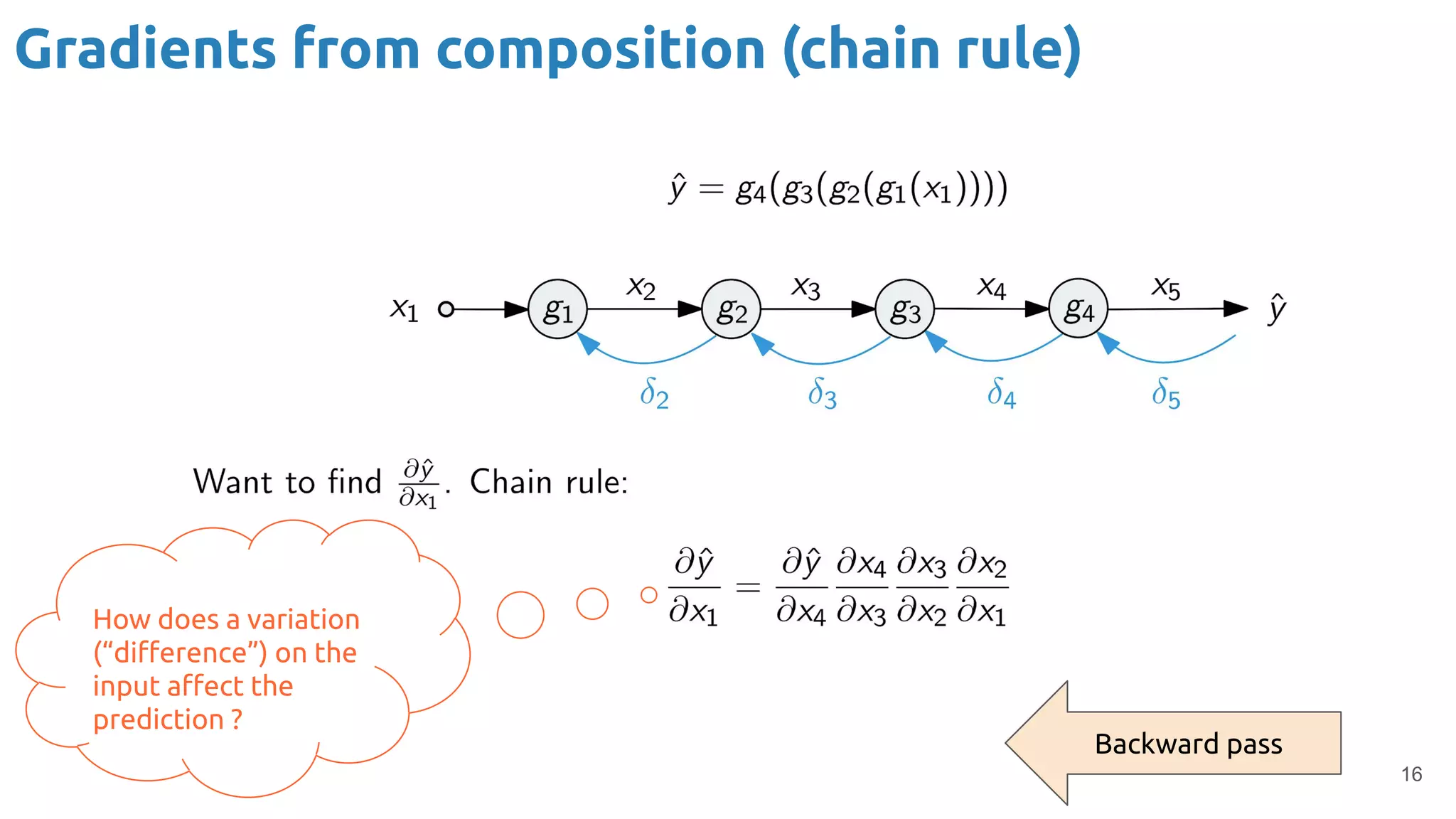
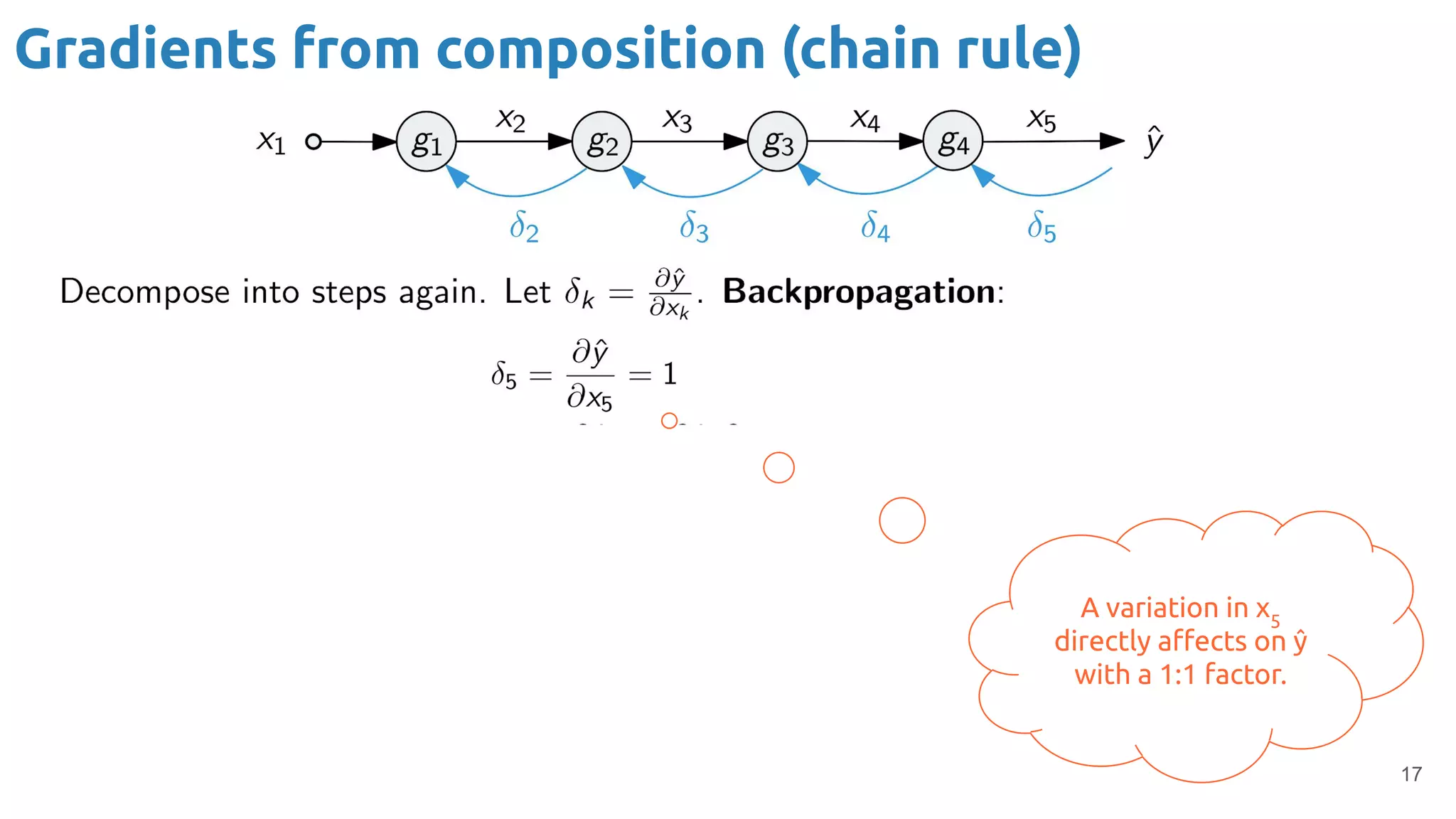
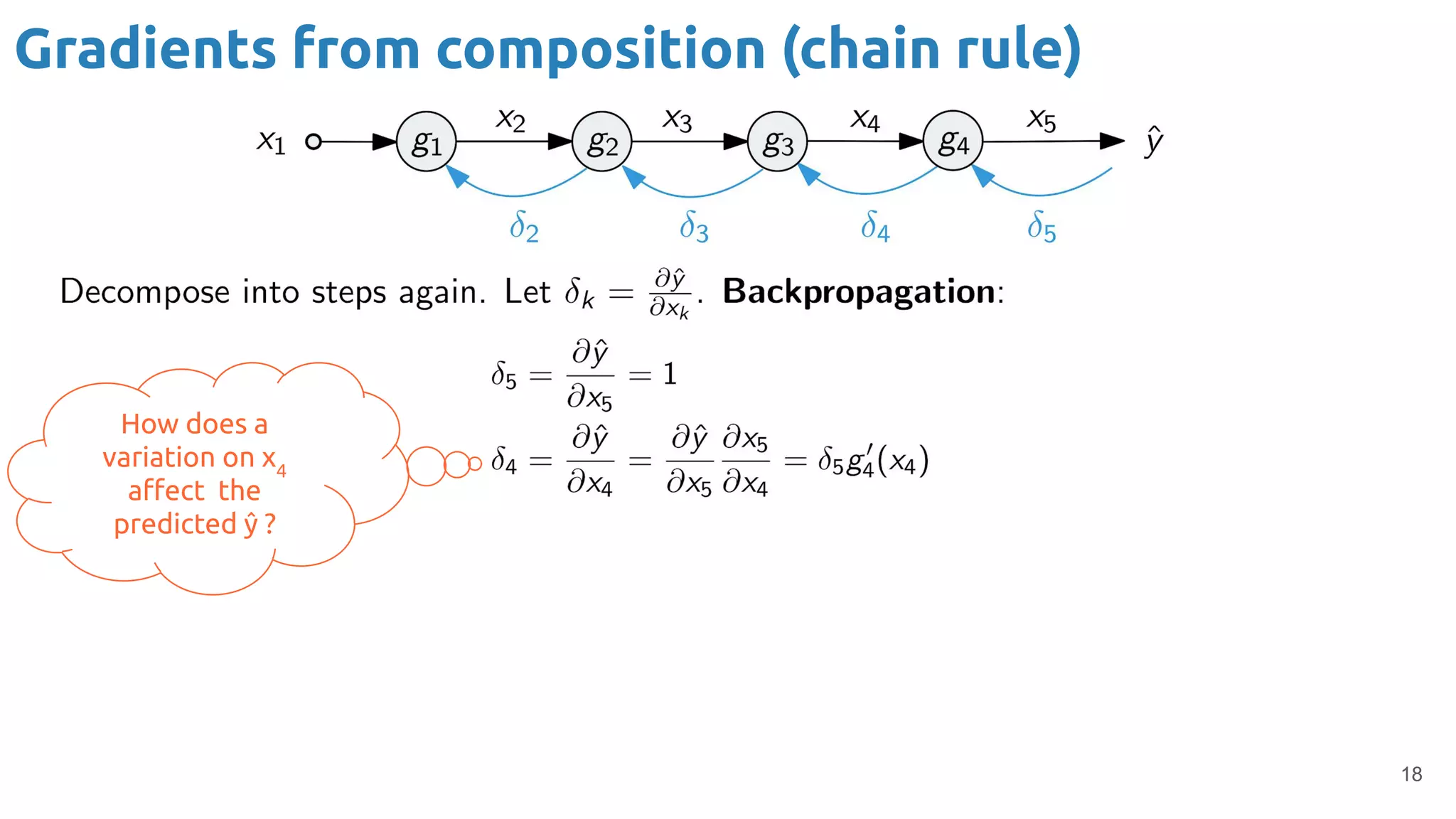
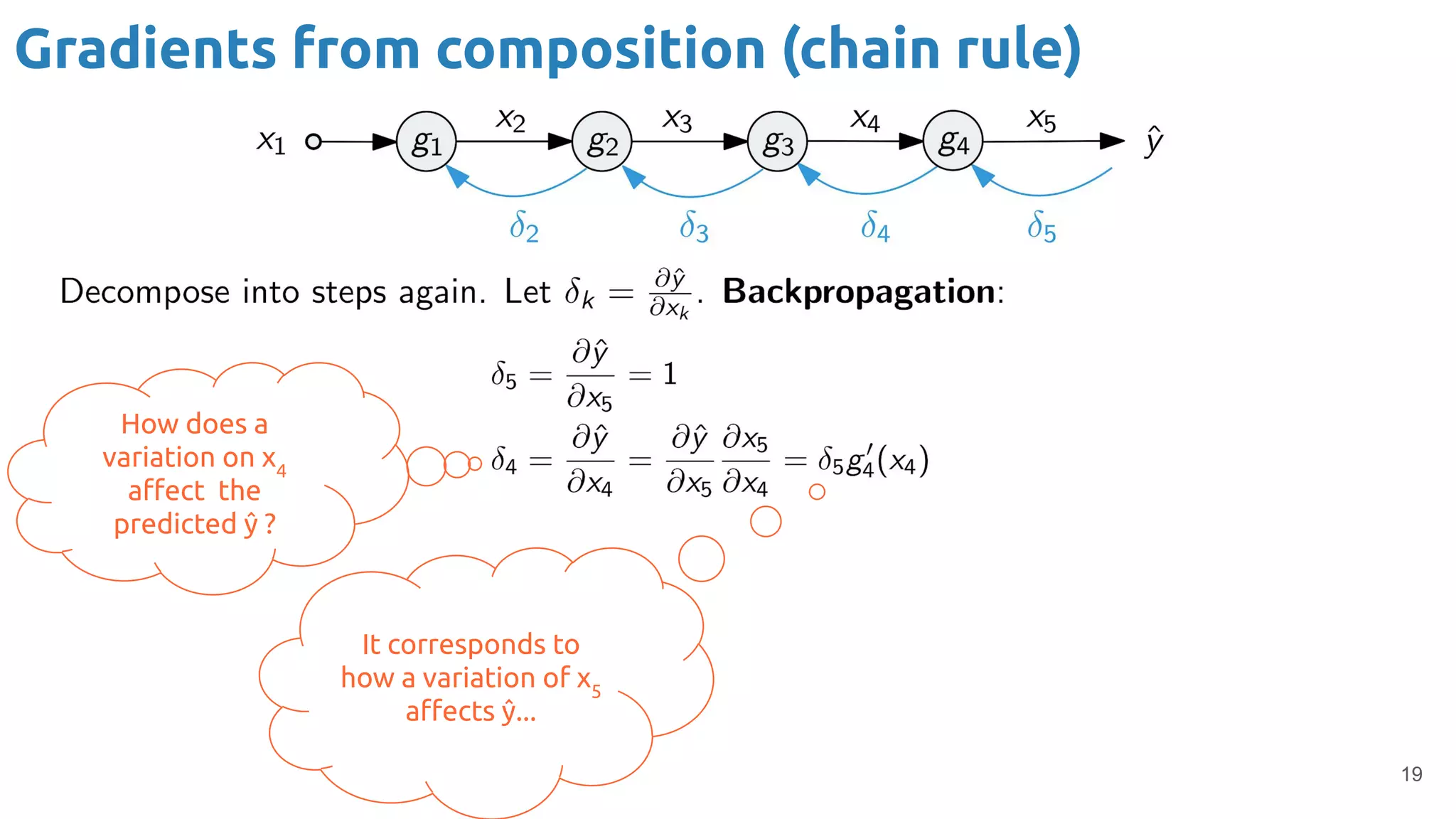
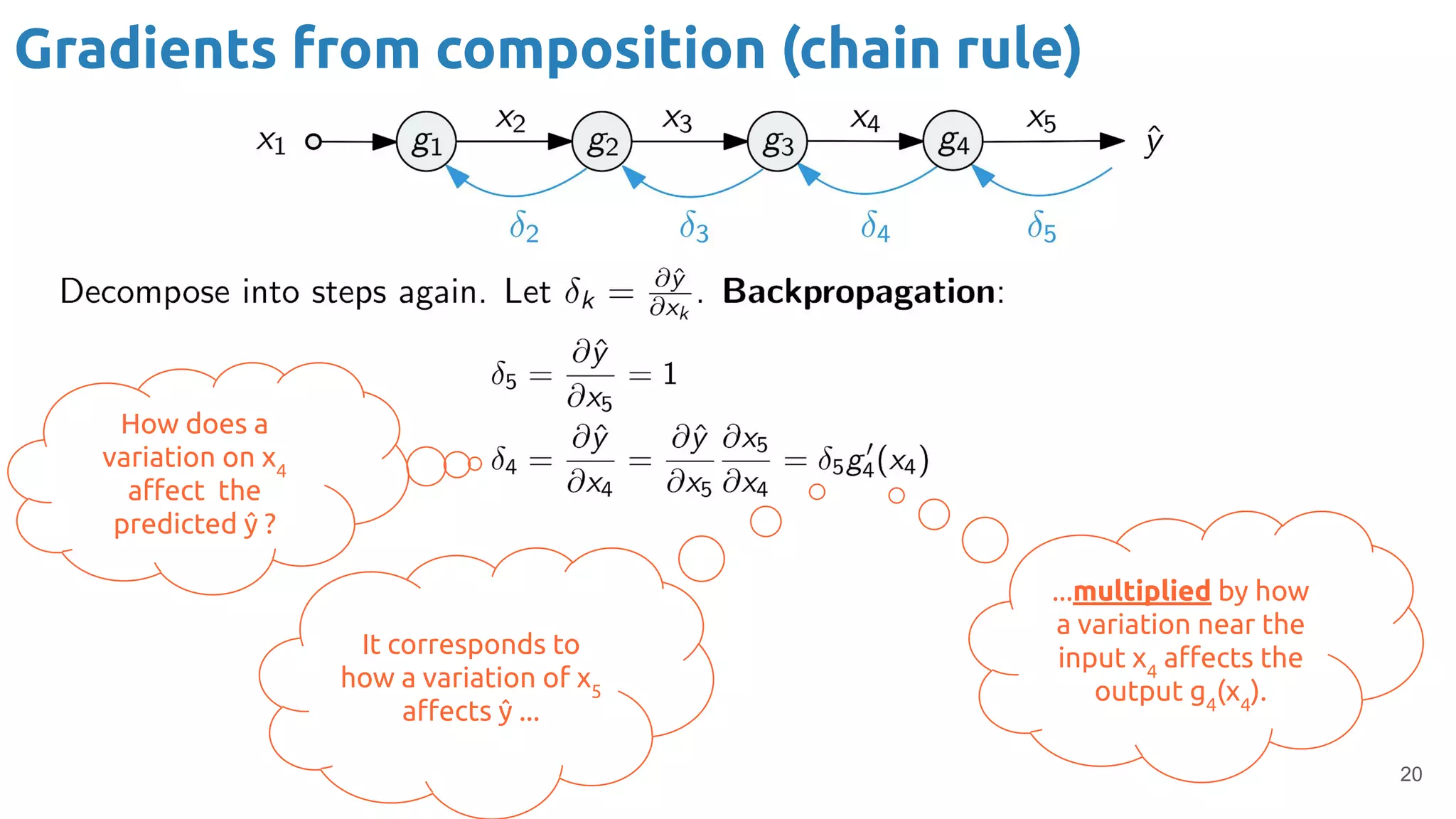
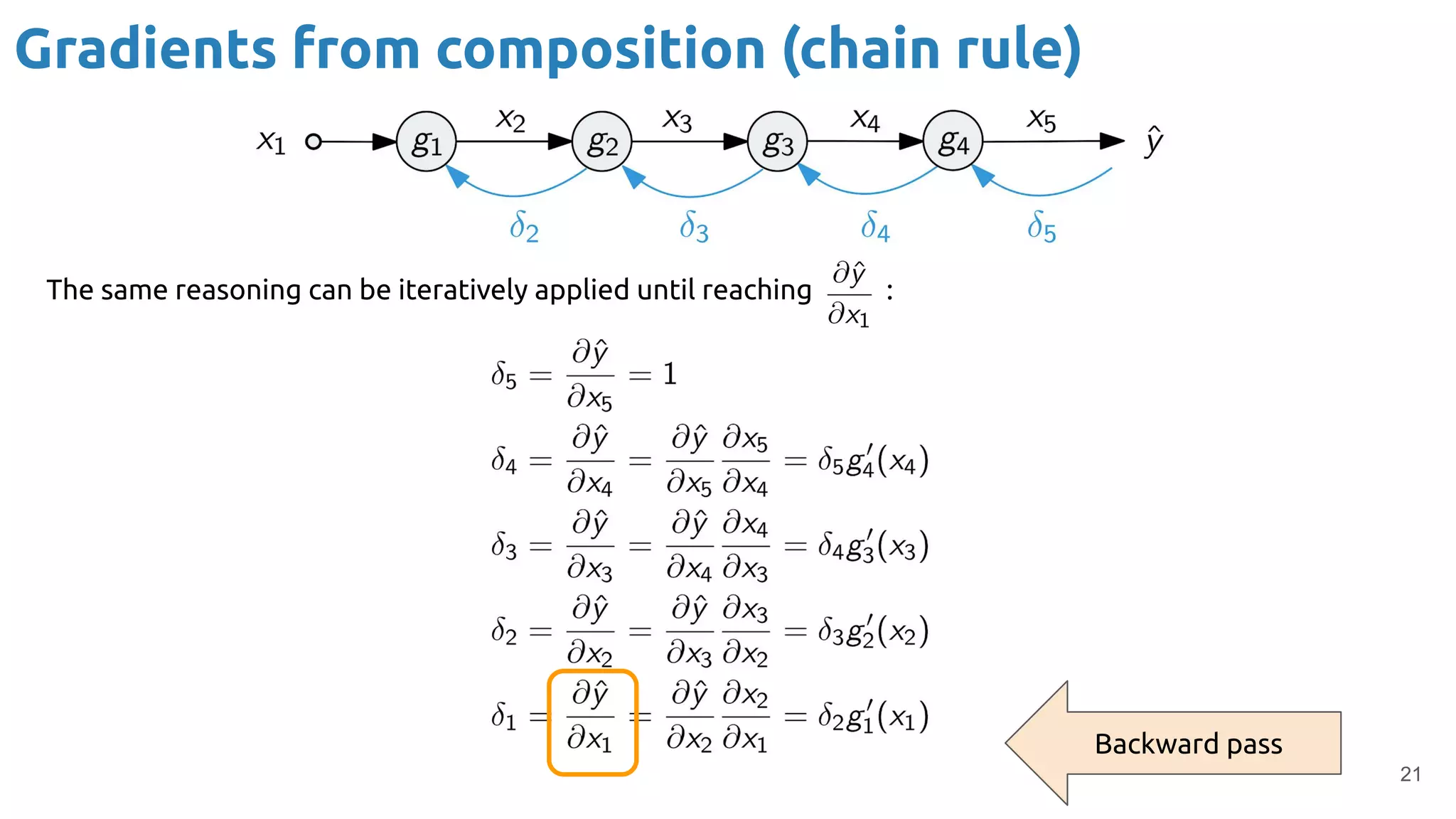
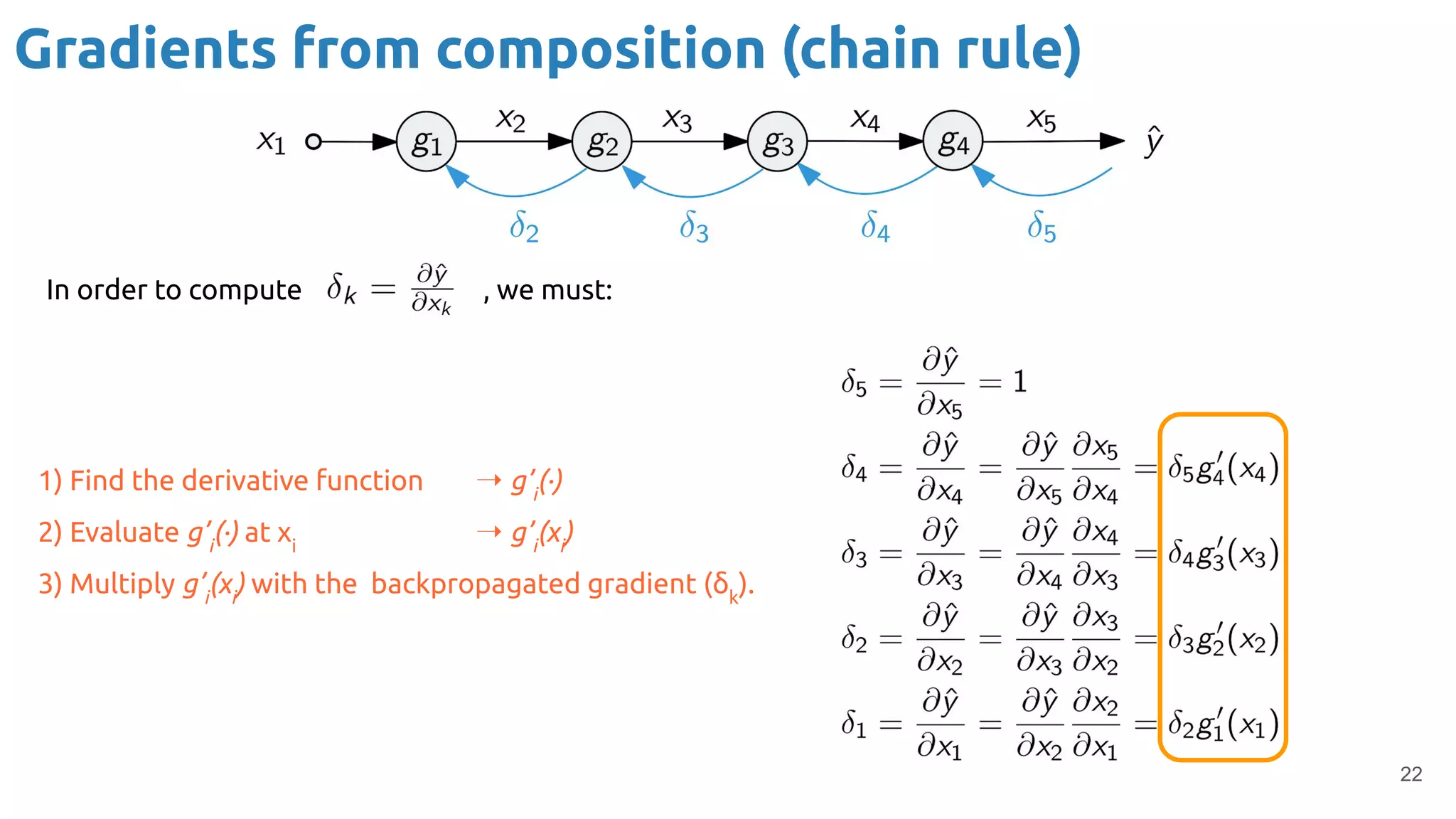
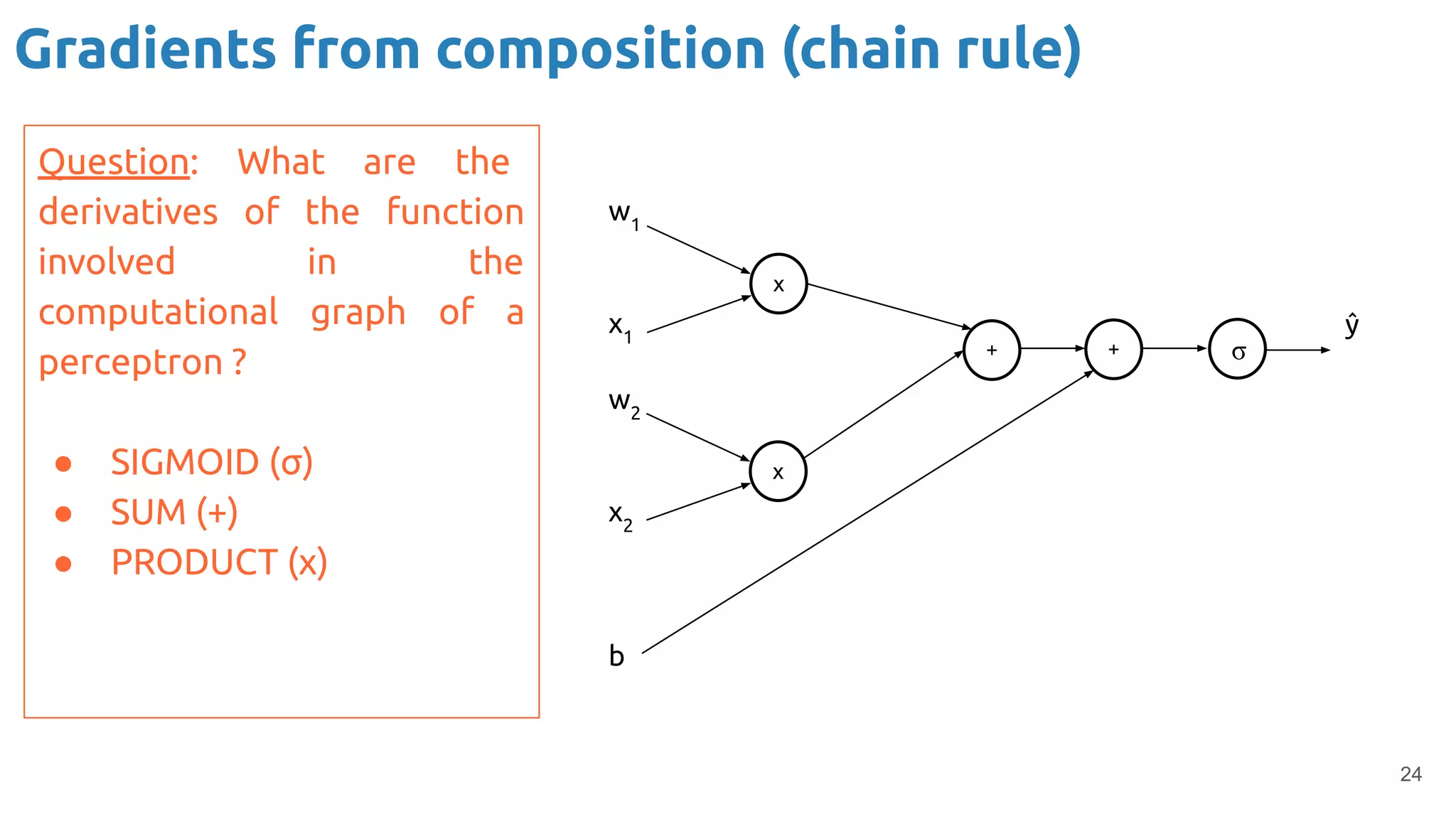
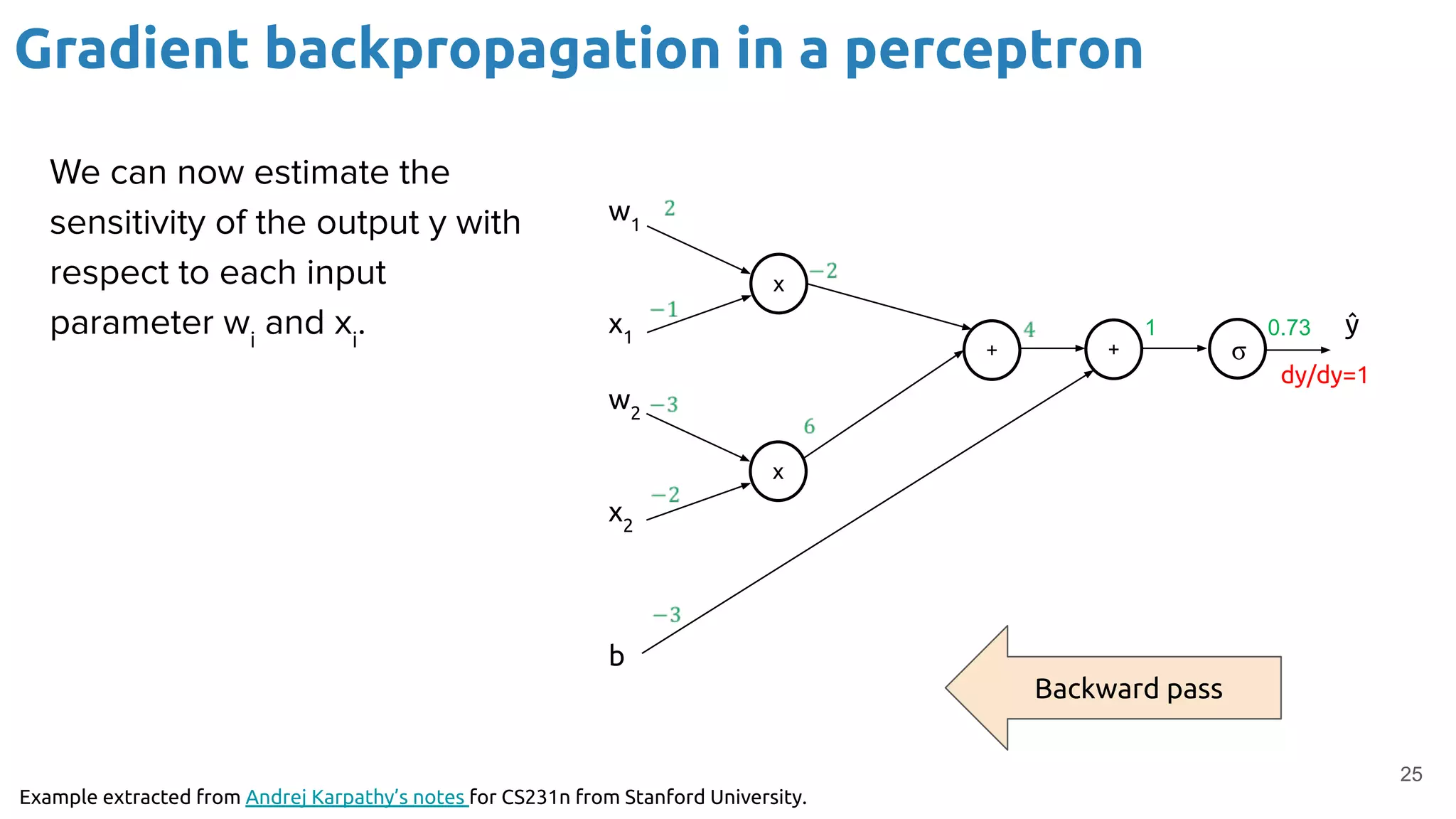
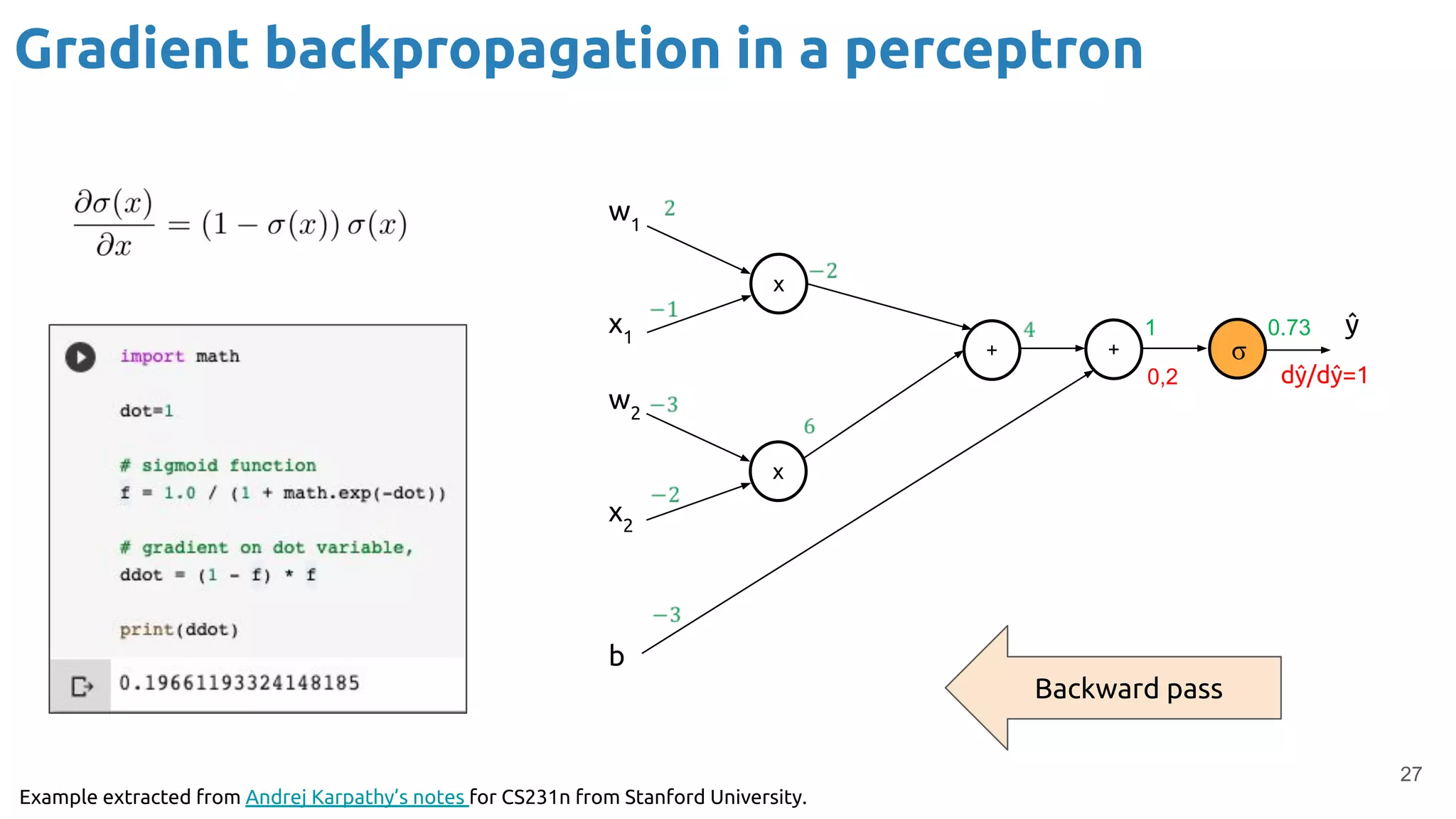
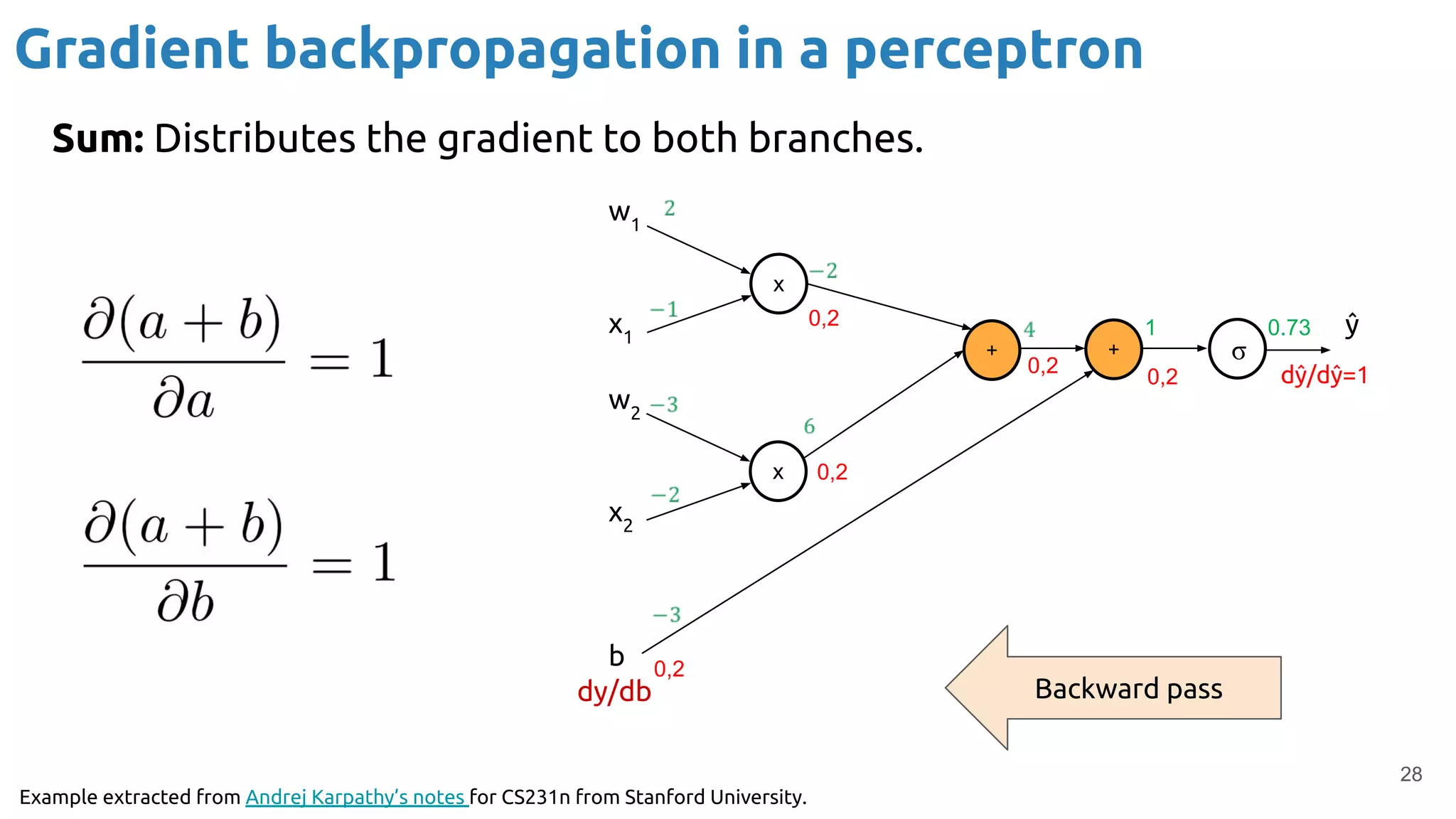
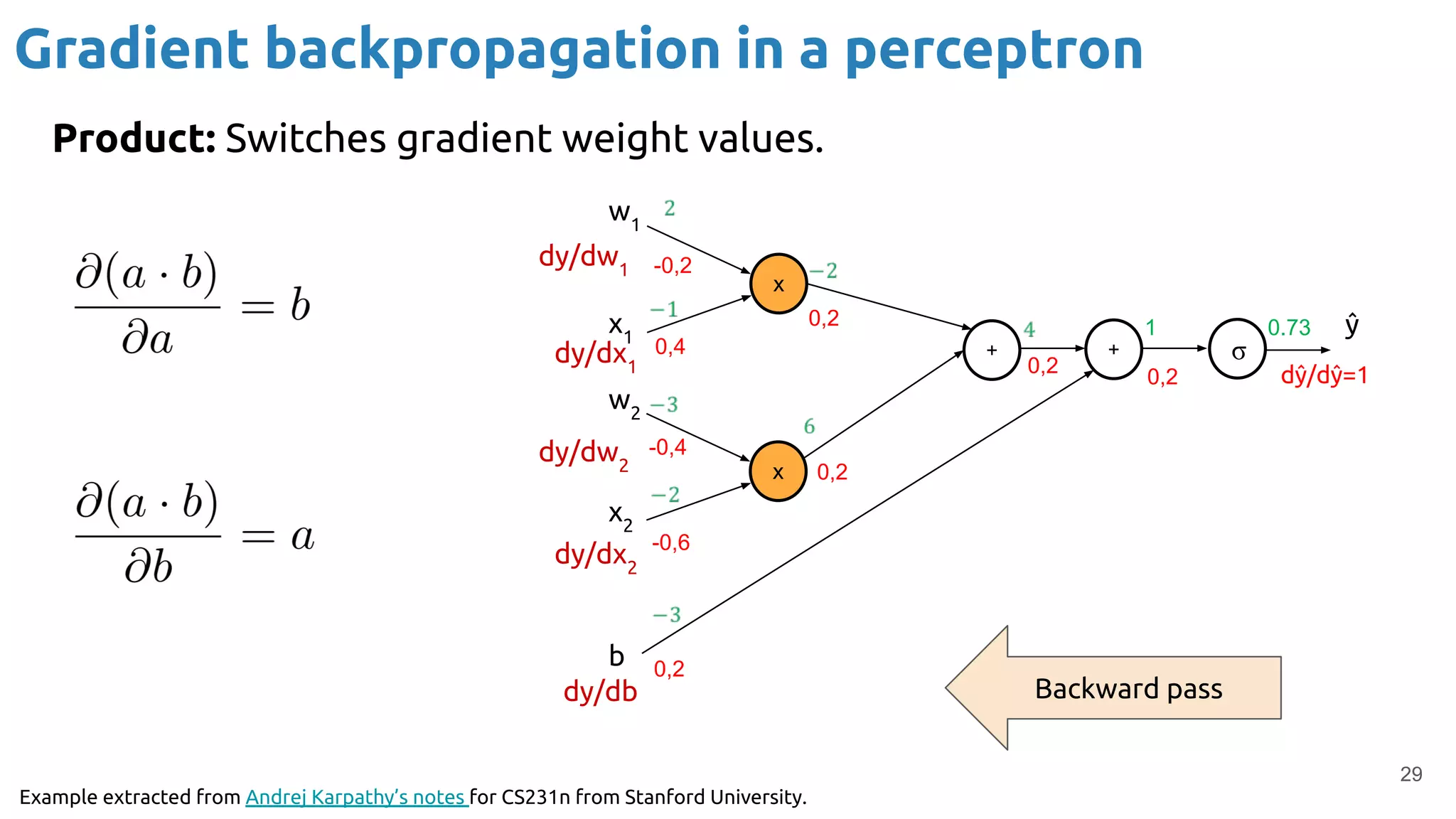
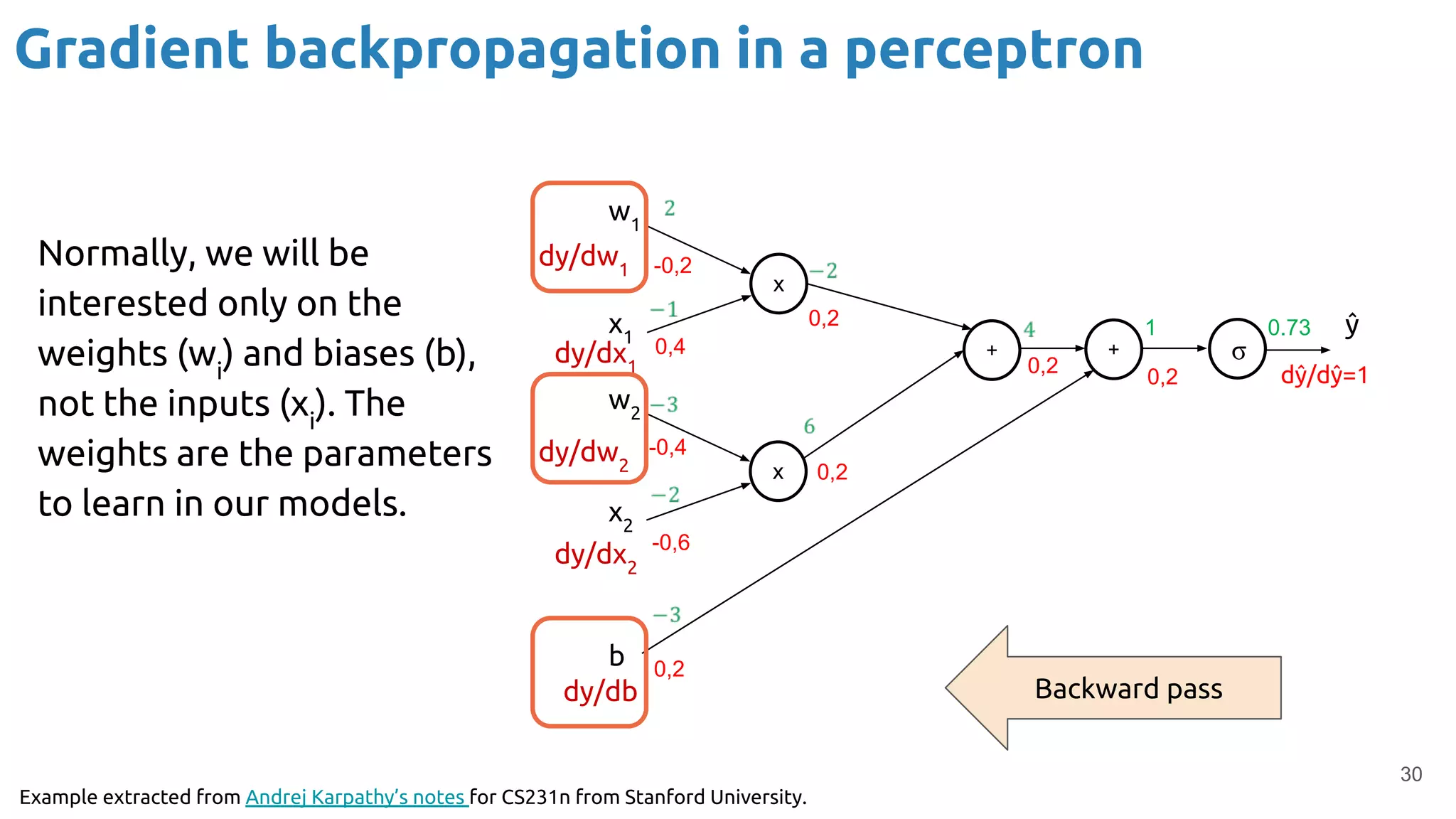
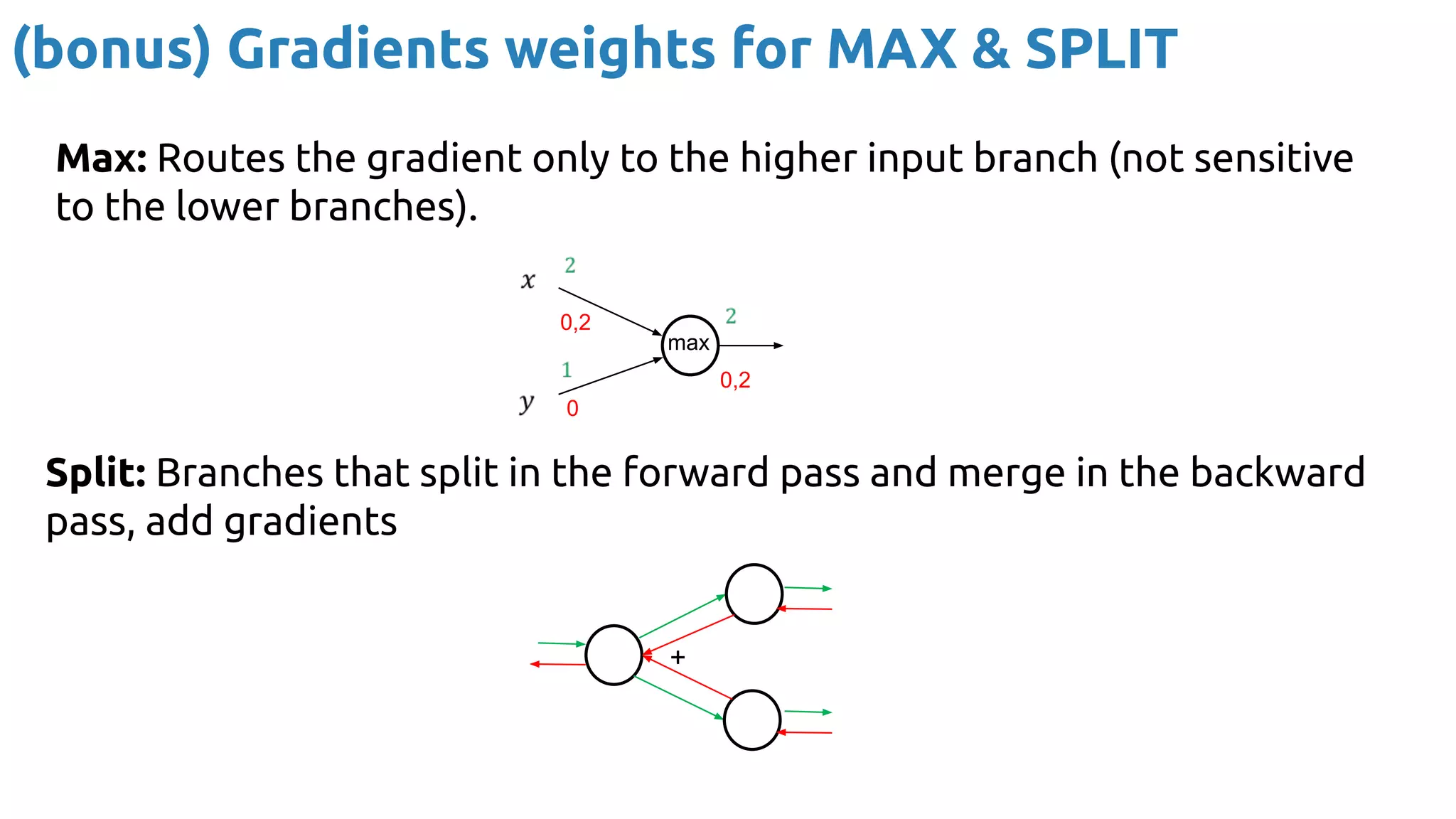
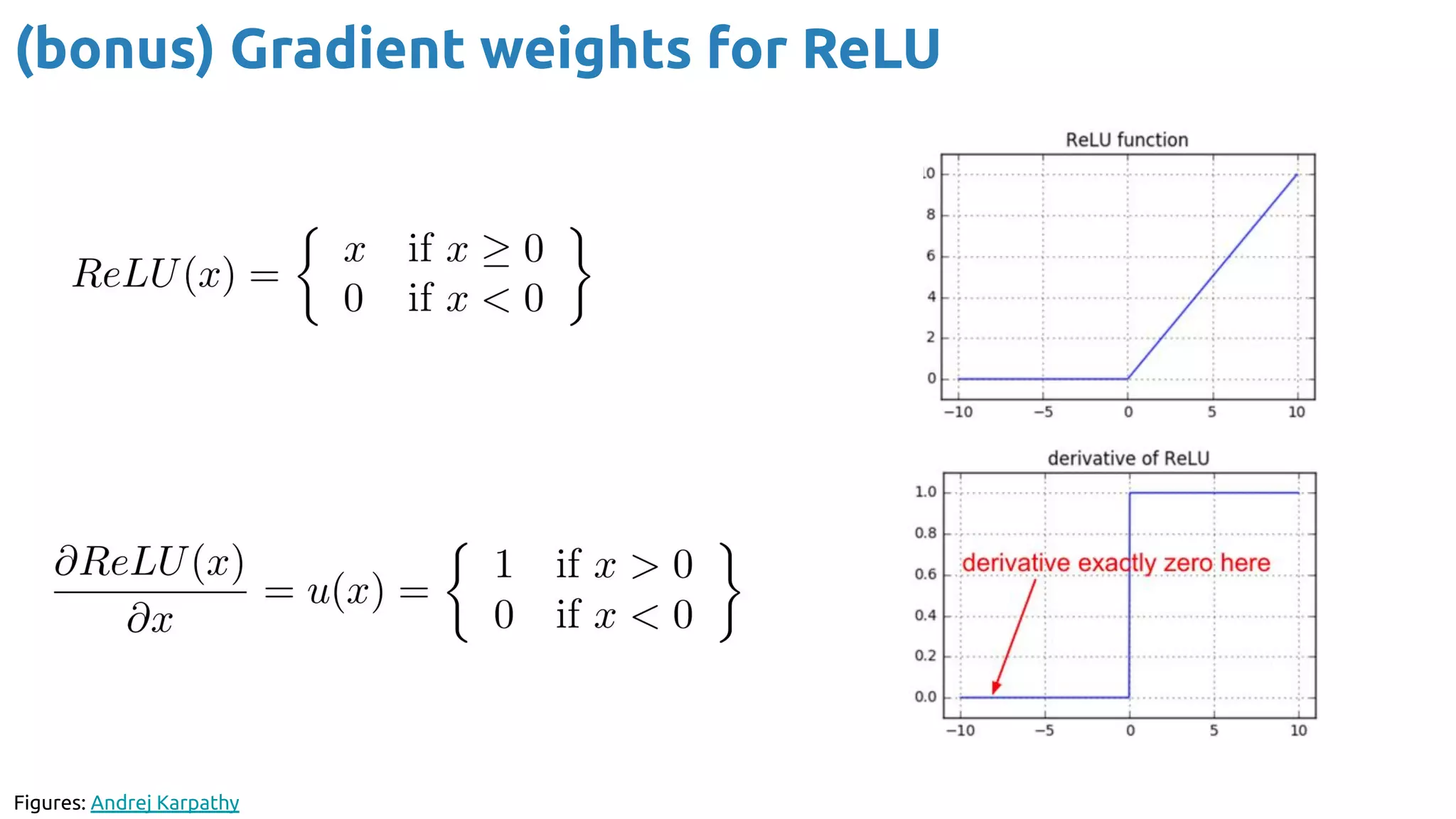
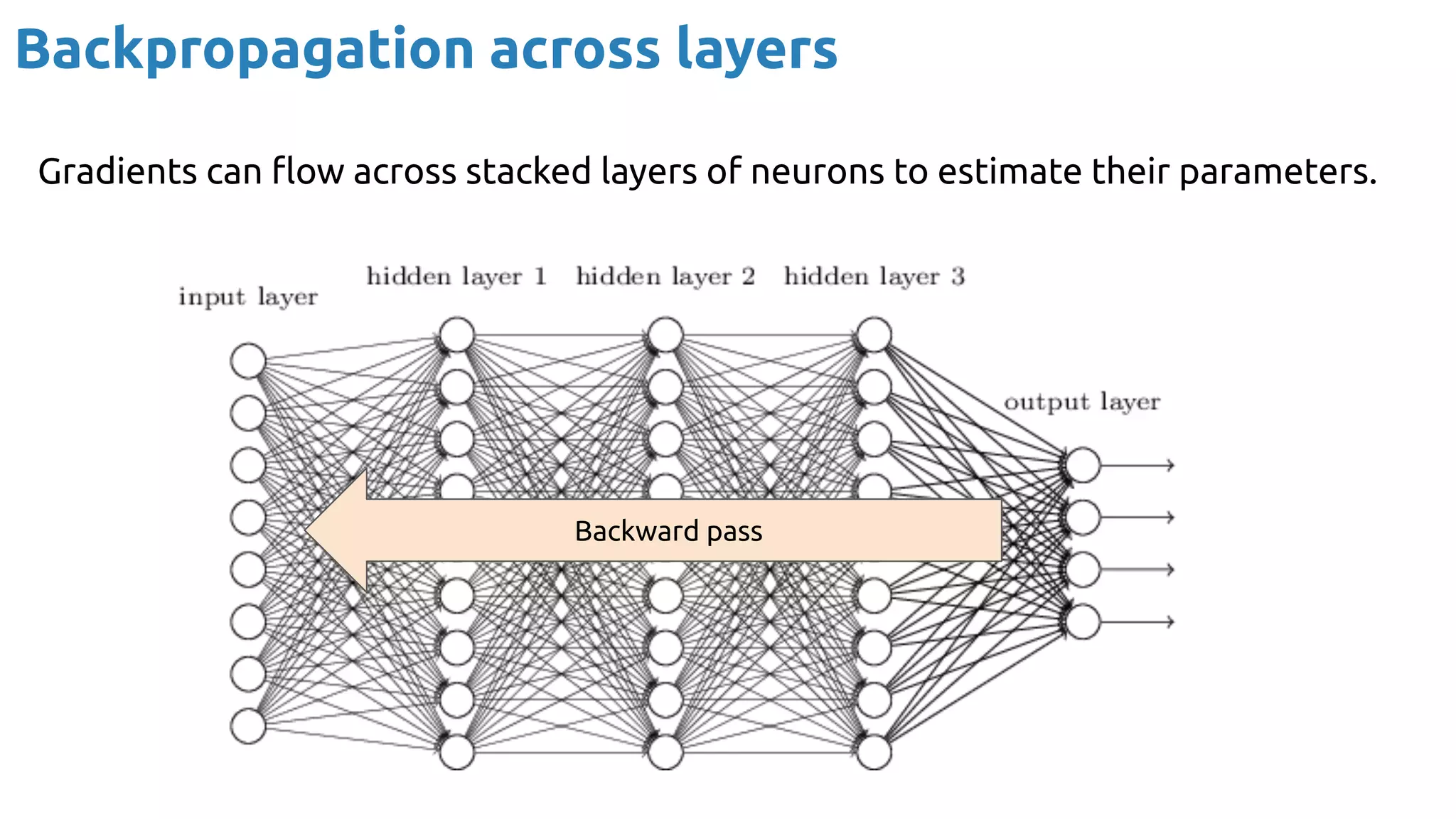
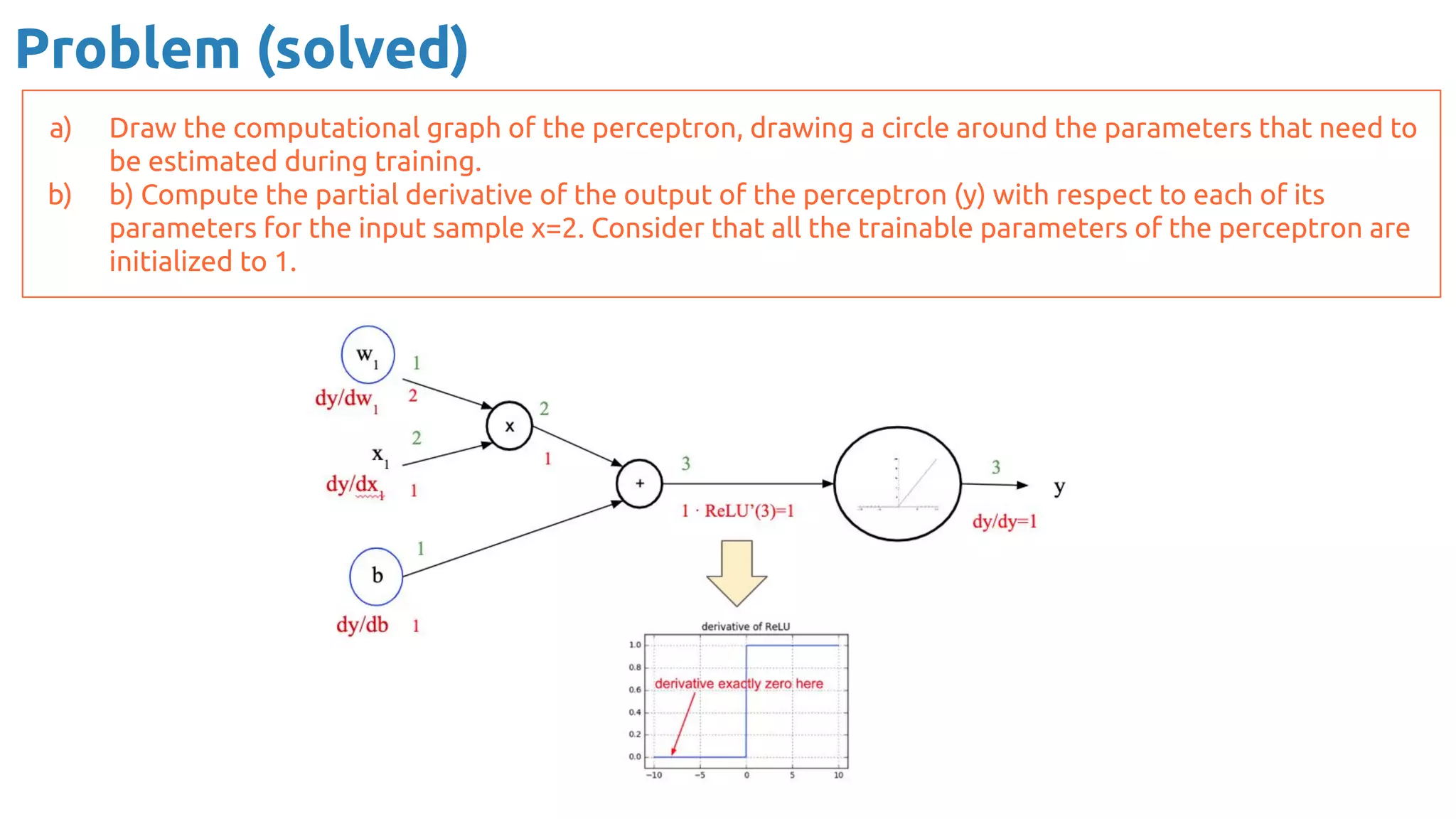
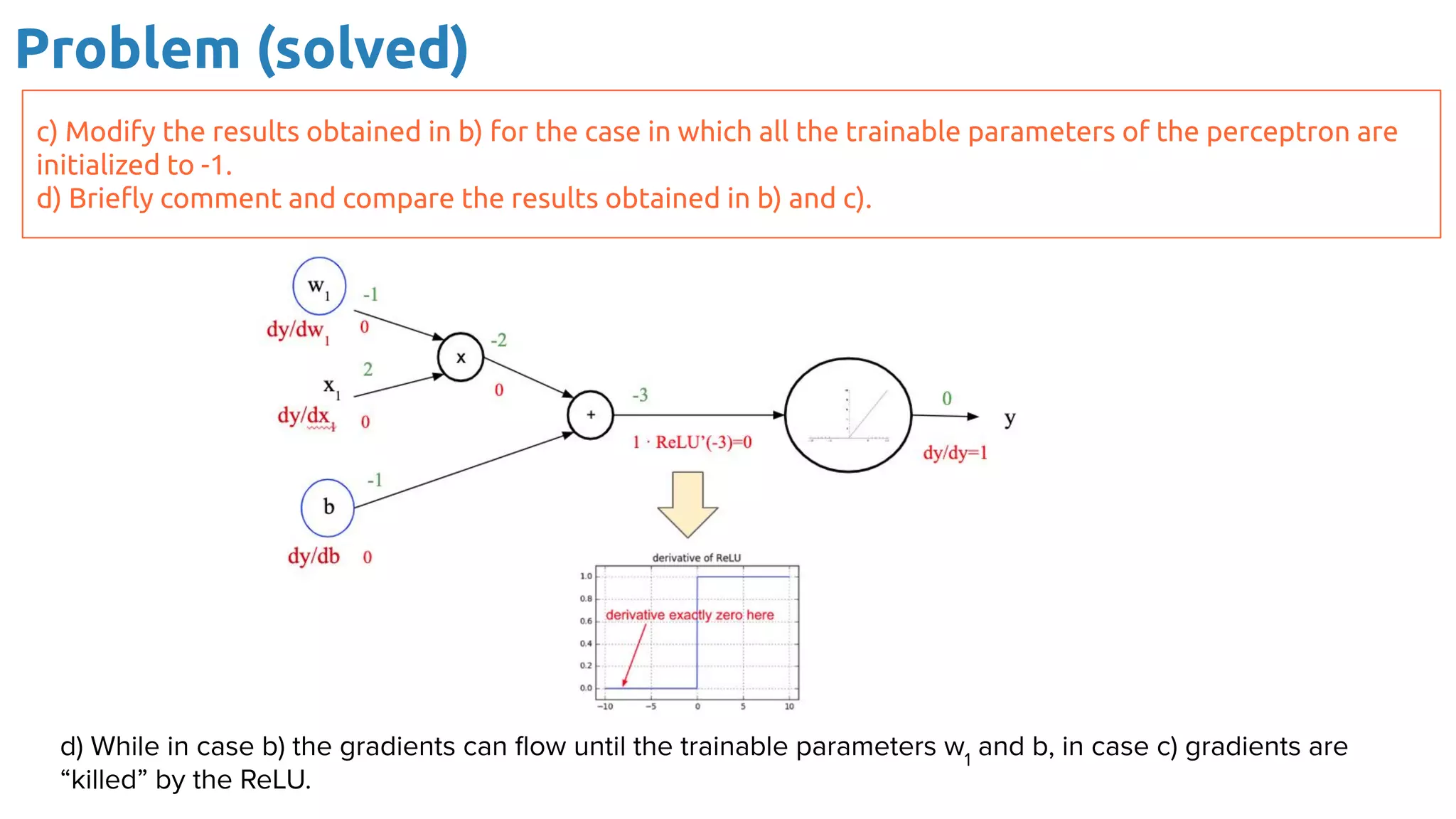
The document provides an overview of backpropagation for neural networks. It begins by defining the loss function and discussing gradient descent. It then walks through the computational graph of a simple perceptron and derives the gradients for each operation using the chain rule. This allows computing the gradient of the loss with respect to the weights and biases, which are then updated using gradient descent. It discusses computing gradients for different activation functions like sigmoid, ReLU, and max pooling. Finally, it notes that backpropagation allows estimating parameters across stacked neural network layers.

1. Backpropagation
Day 2 Lecture 1
http://bit.ly/idl2020
Xavier Giro-i-Nieto
@DocXavi
xavier.giro@upc.edu
Associate Professor
Universitat Politècnica de Catalunya

2. 2
Acknowledgements
Kevin McGuinness
kevin.mcguinness@dcu.ie
Research Fellow
Insight Centre for Data Analytics
Dublin City University
Elisa Sayrol
elisa.sayrol@upc.edu
Associate Professor
ETSETB TelecomBCN
Universitat Politècnica de Catalunya

3. 3
Video lecture

4. Loss function - L(y, ŷ)
The loss function assesses the performance of our model by comparing its
predictions (ŷ) to an expected value (y), typically coming from annotations.
Example: the predicted price (ŷ) and one actually paid (y)
could be compared with the Euclidean distance (also
referred as L2 distance or Mean Square Error - MSE):
1
x1
x2
x3
y = {-∞, ∞}
b
w1
w2
w3

5. Discussion: Consider the
single-parameter model...
…....and that, given a pair (y, ŷ), we would
like to update the current wt
value to a
new wt+1
based on the loss function Lw
.
(a) Would you increase or decrease wt
?
(b) What operation could indicate which
way to go ?
(c) How much would you increase or
decrease wt
?
Loss function - L(y, ŷ)
ŷ = x · w
Lw

6. Motivation for this lecture:
if we had a way to estimate the
gradient of the loss (▽L)with respect
to the parameter(s), we could use
gradient descent to optimize them.
6
Gradient Descent (GD)
Descend
(minus sign)
Learning
rate (LR)
Lw

7. Backpropagation will allow us to compute the gradients of the loss function with
respect to:
● all model parameters (w & b) - final goal during training
● input/intermediate data - visualization & interpretability purposes.
Gradients will “flow” from the output of the model towards the input (“back”).
Gradient Descent (GD)

8. Computational graph of a simple perceptron
8
σ
1
x1
x2
y = {0, 1}
b
w1
w2
Question: What is the computational graph
(operations & order) of this perceptron with a
sigmoid activation ?

9. Computational graph of a perceptron
9
σ
1
x1
x2
y = {0, 1}
b
w1
w2
x
x
w1
x1
w2
x2
Example adapted from “CS231n: Convolutional Neural Networks for Visual Recognition”, Stanford University.

10. 10
σ
1
x1
x2
y = {0, 1}
b
w1
w2
x
+
x
w1
x1
w2
x2
Example adapted from “CS231n: Convolutional Neural Networks for Visual Recognition”, Stanford University.
Computational graph of a perceptron

11. 11
σ
1
x1
x2
y = {0, 1}
b
w1
w2
x
+
x
+
w1
x1
w2
x2
b
Example adapted from “CS231n: Convolutional Neural Networks for Visual Recognition”, Stanford University.
Computational graph of a perceptron

12. 12
σ
1
x1
x2
y = {0, 1}
b
w1
w2
x
+
x
+ σ
w1
x1
w2
x2
b
Example adapted from “CS231n: Convolutional Neural Networks for Visual Recognition”, Stanford University.
y
Computational graph of a perceptron

13. 13
σ
1
x1
x2
y = {0, 1}
b
w1
w2
x
+
x
+ σ
1 0.73
Computational graph of a perceptron
y
Forward pass
w1
x1
w2
x2
b

14. 14
x
+
x
+ σ
Challenge: How to compute
the gradient of the loss
function with respect to w1
or
w2
?
w1
x1
w2
x2
b
y
ŷ
Computational graph of a perceptron

15. 15
Gradients from composition (chain rule)
Forward pass

16. 16
Gradients from composition (chain rule)
How does a variation
(“difference”) on the
input affect the
prediction ?
Backward pass

17. 17
Gradients from composition (chain rule)
A variation in x5
directly affects on ŷ
with a 1:1 factor.

18. 18
Gradients from composition (chain rule)
How does a
variation on x4
affect the
predicted ŷ ?

19. 19
Gradients from composition (chain rule)
How does a
variation on x4
affect the
predicted ŷ ?
It corresponds to
how a variation of x5
affects ŷ...

20. 20
Gradients from composition (chain rule)
...multiplied by how
a variation near the
input x4
affects the
output g4
(x4
).
It corresponds to
how a variation of x5
affects ŷ ...
How does a
variation on x4
affect the
predicted ŷ ?

21. 21
Gradients from composition (chain rule)
Backward pass
The same reasoning can be iteratively applied until reaching :

22. 22
Gradients from composition (chain rule)
In order to compute , we must:
1) Find the derivative function ➝ g’i
(·)
2) Evaluate g’i
(·) at xi
➝ g’i
(xi
)
3) Multiply g’i
(xi
) with the backpropagated gradient (δk
).

23. 23
Gradients from composition (chain rule)
Backward pass
When training NN, we
will actually compute
the derivative over the
loss function, not over
the predicted value ŷ.
L(y, ŷ)

24. 24
Gradients from composition (chain rule)
x
+
x
+ σ
w1
x1
w2
x2
b
Question: What are the
derivatives of the function
involved in the
computational graph of a
perceptron ?
● SIGMOID (σ)
● SUM (+)
● PRODUCT (x)
ŷ

25. 25
Gradient backpropagation in a perceptron
We can now estimate the
sensitivity of the output y with
respect to each input
parameter wi
and xi
.
Example extracted from Andrej Karpathy’s notes for CS231n from Stanford University.
w1
x1
w2
x2
b
x
+
x
+ σ
1 0.73
dy/dy=1
Backward pass
ŷ

26. Gradient weights for sigmoid σ
Even more details: Arunava, “Derivative of the Sigmoid function” (2018)
x
+
x
+ σ
w1
x1
w2
x2
b
...which can be re-arranged as...
(*)
(*)
Figure: Andrej Karpathy
ŷ

27. 27
Gradient backpropagation in a perceptron
w1
x1
w2
x2
b
x
+
x
+ σ
1 0.73
0,2
Example extracted from Andrej Karpathy’s notes for CS231n from Stanford University.
Backward pass
ŷ
dŷ/dŷ=1

28. 28
Sum: Distributes the gradient to both branches.
w1
x1
w2
x2
b
x
+
x
+ σ
1 0.73
0,2
0,2
0,2
0,2
Gradient backpropagation in a perceptron
Example extracted from Andrej Karpathy’s notes for CS231n from Stanford University.
Backward passdy/db
0,2
ŷ
dŷ/dŷ=1

29. 29
x
+
x
+ σ
1 0.73
0,2
0,2
0,2
-0,2
0,2
0,2
0,4
-0,4
-0,6
Product: Switches gradient weight values.
Gradient backpropagation in a perceptron
Example extracted from Andrej Karpathy’s notes for CS231n from Stanford University.
Backward pass
w1
x1
w2
x2
b
dy/dw1
dy/dx1
dy/dw2
dy/dx2
dy/db
ŷ
dŷ/dŷ=1

30. 30
w1
x1
w2
x2
b
x
+
x
+ σ
1 0.73
0,2
0,2
0,2
-0,2
0,2
0,2
0,4
-0,4
-0,6
dŷ/dŷ=1
Gradient backpropagation in a perceptron
Example extracted from Andrej Karpathy’s notes for CS231n from Stanford University.
Normally, we will be
interested only on the
weights (wi
) and biases (b),
not the inputs (xi
). The
weights are the parameters
to learn in our models.
Backward pass
dy/dw1
dy/dx1
dy/dw2
dy/dx2
dy/db
ŷ

31. (bonus) Gradients weights for MAX & SPLIT
0,2
0,2
0
max
Max: Routes the gradient only to the higher input branch (not sensitive
to the lower branches).
Split: Branches that split in the forward pass and merge in the backward
pass, add gradients
+

32. (bonus) Gradient weights for ReLU
Figures: Andrej Karpathy

33. Backpropagation across layers
Backward pass
Gradients can flow across stacked layers of neurons to estimate their parameters.

34. Watch more
34
Gilbert Strang, “27. Backpropagation: Find
Partial Derivatives”. MIT 18.065 (2018)
Creative Commons, “Yoshua Bengio Extra
Footage 1: Brainstorm with students” (2018)

35. Learn more
35
READ
● Chris Olah, “Calculus on Computational Graphs: Backpropagation” (2015).
● Andrej Karpathy,, “Yes, you should understand backprop” (2016), and his “course notes at
Stanford University CS231n.
THREAD

36. Advanced discussion
36

37. Problem
Consider a perceptron with a ReLU as activation function designed to process a single-dimensional inputs x.
a) Draw the computational graph of the perceptron, drawing a circle around the parameters that need to
be estimated during training.
b) Compute the partial derivative of the output of the perceptron (y) with respect to each of its
parameters for the input sample x=2. Consider that all the trainable parameters of the perceptron are
initialized to 1.
c) Modify the results obtained in b) for the case in which all the trainable parameters of the perceptron
are initialized to -1.
d) Briefly comment and compare the results obtained in b) and c).

38. Problem (solved)
a) Draw the computational graph of the perceptron, drawing a circle around the parameters that need to
be estimated during training.
b) b) Compute the partial derivative of the output of the perceptron (y) with respect to each of its
parameters for the input sample x=2. Consider that all the trainable parameters of the perceptron are
initialized to 1.

39. Problem (solved)
c) Modify the results obtained in b) for the case in which all the trainable parameters of the perceptron are
initialized to -1.
d) Briefly comment and compare the results obtained in b) and c).
d) While in case b) the gradients can flow until the trainable parameters w1
and b, in case c) gradients are
“killed” by the ReLU.