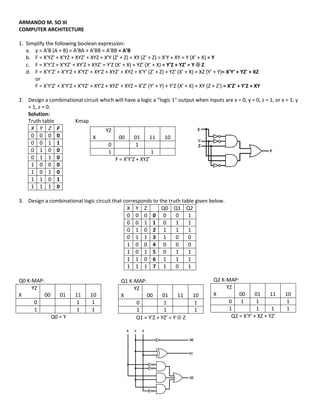
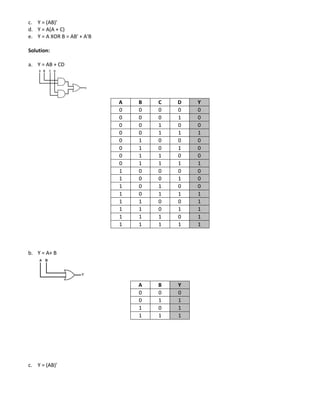
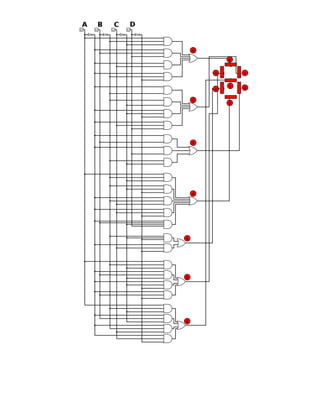
The document contains examples and solutions to problems involving boolean algebra, combinational logic circuits, binary number systems, and basic digital logic components like flip-flops. Some key points: - It provides solutions to simplifying boolean expressions and designing combinational logic circuits from truth tables. - Examples are given for binary coded decimal to seven segment decoding and frequency point calculations based on input frequency division. 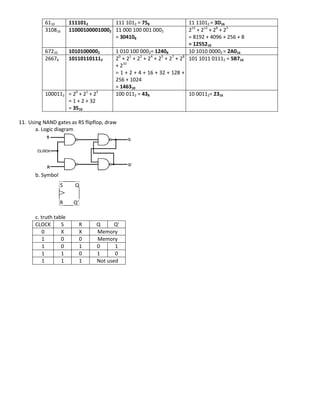- Conversions between binary, decimal, and hexadecimal number systems are demonstrated. - The logic diagram, symbol, and truth table for an RS flip-flop implemented with NAND gates is illustrated.

1. ARMANDO M. SO III
COMPUTER ARCHITECTURE
1. Simplify the following boolean expression:
a. y = A'B (A + B) = A'BA + A'BB = A'BB = A'B
b. F = X'YZ' + X'YZ + XYZ' + XYZ = X'Y (Z' + Z) + XY (Z' + Z) = X'Y + XY = Y (X' + X) = Y
c. F = X'Y'Z + X'YZ' + XY'Z + XYZ' = Y'Z (X' + X) + YZ' (X' + X) = Y'Z + YZ' = Y  Z
d. F = X'Y'Z' + X'Y'Z + X'YZ' + XY'Z + XYZ' + XYZ = X'Y' (Z' + Z) + YZ' (X' + X) + XZ (Y' + Y)= X'Y' + YZ' + XZ
or
F = X'Y'Z' + X'Y'Z + X'YZ' + XY'Z + XYZ' + XYZ = X'Z' (Y' + Y) + Y'Z (X' + X) + XY (Z + Z') = X'Z' + Y'Z + XY
2. Design a combinational circuit which will have a logic a "logic 1" output when inputs are x = 0, y = 0, z = 1, or x = 1, y
= 1, z = 0.
Solution:
Truth table Kmap
X Y Z F
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 0
3. Design a combinational logic circuit that corresponds to the truth table given below.
X Y Z Q0 Q1 Q2
0 0 0 0 0 0 1
0 0 1 1 0 1 1
0 1 0 2 1 1 1
0 1 1 3 1 0 0
1 0 0 4 0 0 0
1 0 1 5 0 1 1
1 1 0 6 1 1 1
1 1 1 7 1 0 1
Q0 K-MAP:
YZ
X 00 01 11 10
0 1 1
1 1 1
Q0 = Y
YZ
X 00 01 11 10
0 1
1 1
F = X'Y'Z + XYZ'
Q2 K-MAP:
YZ
X 00 01 11 10
0 1 1 1
1 1 1 1
Q2 = X'Y' + XZ + YZ'
Q1 K-MAP:
YZ
X 00 01 11 10
0 1 1
1 1 1
Q1 = Y'Z + YZ' = Y  Z

2. 4. Design a binary coded decimal (BCD) to seven segment decoder.
Solution:
INPUT SEGMENT
A B C D 0 - TOP 1 - UR 2 - LR 3 - BOT 4 - LL 5 - UL 6 - MID
0 0 0 0 1 1 1 1 1 1 0
0 0 0 1 0 1 1 0 0 0 0
0 0 1 0 1 1 0 1 1 0 1
0 0 1 1 1 1 1 1 0 0 1
0 1 0 0 0 1 1 0 0 1 1
0 1 0 1 1 0 1 1 0 1 1
0 1 1 0 1 0 1 1 1 1 1
0 1 1 1 1 1 1 0 0 0 0
1 0 0 0 1 1 1 1 1 1 1
1 0 0 1 1 1 1 1 0 1 1
SEGMENT 0 (TOP)
CD
AB 00 01 11 10
00 1 1 1
01 1 1 1
11
10 1 1
AB’C’ + A’BD + A’C + A’B’D’
SEGMENT 1 (UR)
CD
AB 00 01 11 10
00 1 1 1 1
01 1 1
11
10 1 1
A'B'+B'C'+A'C'D'+A'CD
SEGMENT 2 (LR)
CD
AB 00 01 11 10
00 1 1 1
01 1 1 1 1
11
10 1 1
A’B + A’D + B’C’
SEGMENT 3 (BOTTOM)
CD
AB 00 01 11 10
00 1 1 1
01 1 1
11
10 1 1
AB’C’+B’C’D’+A’B’C+A’CD’+A’BC’D
SEGMENT 4 (LL)
CD
AB 00 01 11 10
00 1 1
01 1
11
10 1
B’C’D’ + A’CD’
SEGMENT 5 (UL)
CD
AB 00 01 11 10
00 1
01 1 1 1
11
10 1 1
AB’C’ + A’BC’ + A’C’D’ + A’BD’
SEGMENT 6 (MIDDLE)
CD
AB 00 01 11 10
00 1 1
01 1 1 1
11
10 1 1
AB’C’ + A’BC’ + A’B’C + A’CD’

3. 0
1
2
3
4
5
6
0
1
2
3
04
5
6

4. 5. Given the Boolean expression below
F1 = AB + B
F2 = (AB' + C)(A + B')C
F3 = AB + (B' + C') + A'C
a. Simplify the expression using boolean algebra and implement using maximum of two levels of logic.
b. Using NAND to implement these functions and show the diagram.
Solution:
a. F1 = AB + B = B (A + 1) = B
F2 = (AB' +C)(A + B')C = C(AB' + C)(A + B') = (AB'C + C)(A + B')= C(AB' + 1)(A + B') = C(A + B')
F3 = AB + (B' + C') + A'C = AB + B' + C' + A'C = B' + AB + C' + A'C = (B' + A)(B' + B) + (C' + A') = A + B' + A' + C'
= A' + A + B' + C' = 1 + B' + C'= 1
b.
6. Illustrate or represent symbolically the following function switching system.
a. AND function b. OR function c. NOT function
d. MEMORY function e. TIME DELAY function
Solution:
a. AND function
b. OR function
c. NOT function
d. MEMORY function

5. e. TIME DELAY function
7. Find the truth table for the circuit output Y. Show your solution, use positive logic.
Solution:
Y = A'BC + (A  B  C) + D
A B C D Y = A'BC
0 1 1 X 1
A B C D K = A  B Y = K  C
0 0 1 X 0 1
0 1 0 X 1 1
1 0 0 X 1 1
1 1 1 X 0 1
A B C D Y = D
X X X 1 1
Truth Table:
A B C D Y
0 0 0 0 0
0 0 0 1 1
0 0 1 0 1
0 0 1 1 1
0 1 0 0 1
0 1 0 1 1
0 1 1 0 1
0 1 1 1 1
1 0 0 0 1
1 0 0 1 1
1 0 1 0 0
1 0 1 1 1
1 1 0 0 0
1 1 0 1 1
1 1 1 0 1
1 1 1 1 1
8. Give the equivalent binary logic gate symbol combinations, corresponding truth tables, and significant meaning of
the truth tables for the following expressions.
a. Y = AB + CD
b. Y = A+ B

6. c. Y = (AB)'
d. Y = A(A + C)
e. Y = A XOR B = AB' + A'B
Solution:
a. Y = AB + CD
A B C D Y
0 0 0 0 0
0 0 0 1 0
0 0 1 0 0
0 0 1 1 1
0 1 0 0 0
0 1 0 1 0
0 1 1 0 0
0 1 1 1 1
1 0 0 0 0
1 0 0 1 0
1 0 1 0 0
1 0 1 1 1
1 1 0 0 1
1 1 0 1 1
1 1 1 0 1
1 1 1 1 1
b. Y = A+ B
A B Y
0 0 0
0 1 1
1 0 1
1 1 1
c. Y = (AB)'

7. C B Y
0 0 1
0 1 1
1 0 1
1 1 0
d. Y = A(A + C) = A + AC = A
or
A C Y
0 0 0
0 1 0
1 0 1
1 1 1
e. Y = A XOR B
or
A B Y
0 0 0
0 1 1
1 0 1
1 1 0
9. Given the input frequency of 4800 Hz. Determine the frequency points A, B, C and D.
at A F = (F/2) = 4800 / 2 = 2400 hz
at B F = (F/4) = 4800 / 4 = 1200 hz
at C F = (F/8) = 4800 / 8 = 600 hz
at D F = (F/16) = 4800 / 16 = 300 hz
10. Convert the following numbers as indicated (show solutions)

8. 6110 1111012 111 1012 = 758 11 11012 = 3D16
310816 110001000010002 11 000 100 001 0002
= 304108
213
+ 212
+ 28
+ 23
= 8192 + 4096 + 256 + 8
= 1255210
67210 10101000002 1 010 100 0002= 12408 10 1010 00002 = 2A016
26678 101101101112 20
+ 21
+ 22
+ 24
+ 25
+ 27
+ 28
+ 210
= 1 + 2 + 4 + 16 + 32 + 128 +
256 + 1024
= 146310
101 1011 01112 = 5B716
1000112 = 20
+ 21
+ 25
= 1 + 2 + 32
= 3510
100 0112 = 438 10 00112= 2316
11. Using NAND gates as RS flipflop, draw
a. Logic diagram
b. Symbol
c. truth table
CLOCK S R Q Q'
0 X X Memory
1 0 0 Memory
1 0 1 0 1
1 1 0 1 0
1 1 1 Not used
S
R
Q
Q'