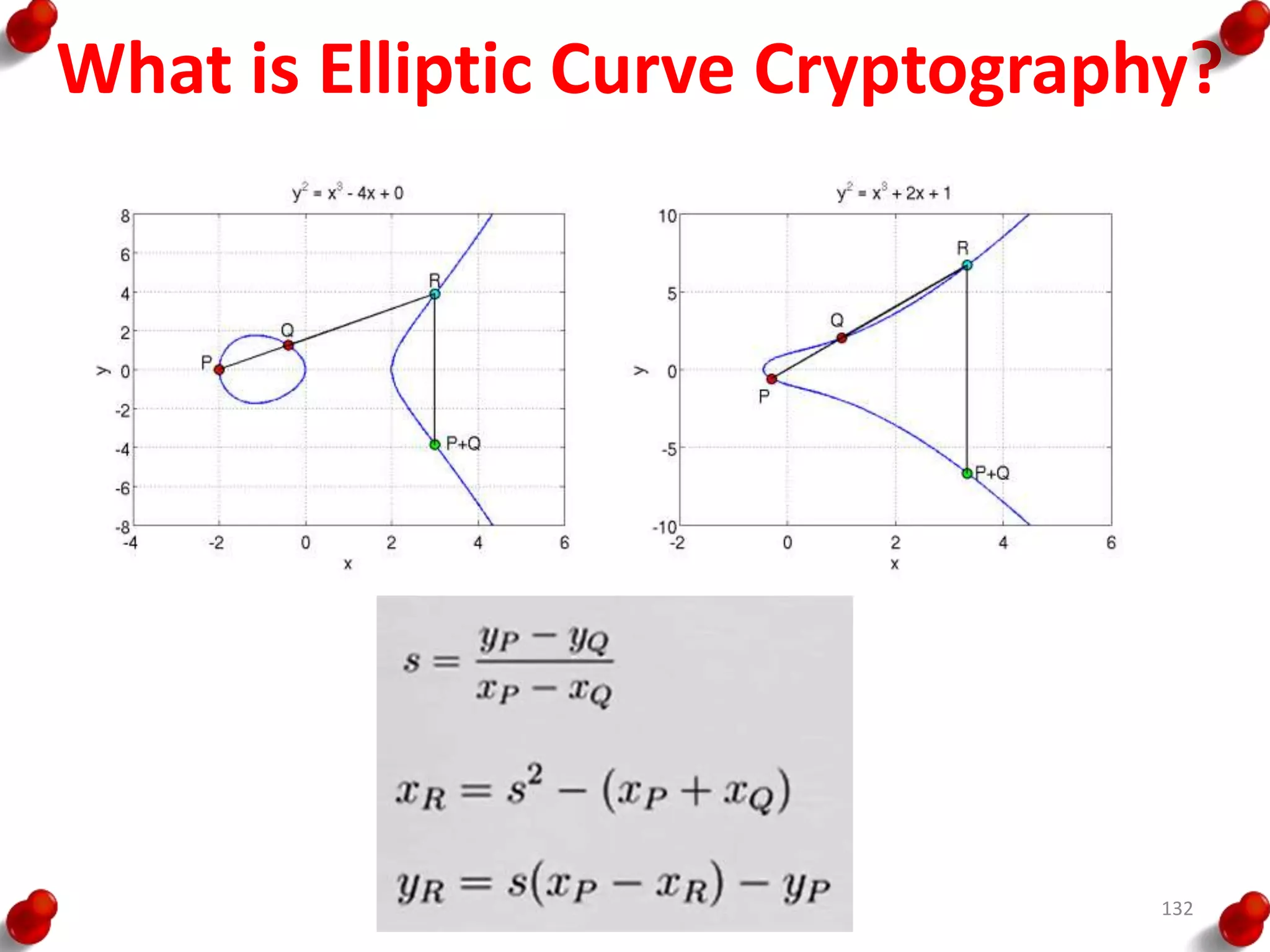
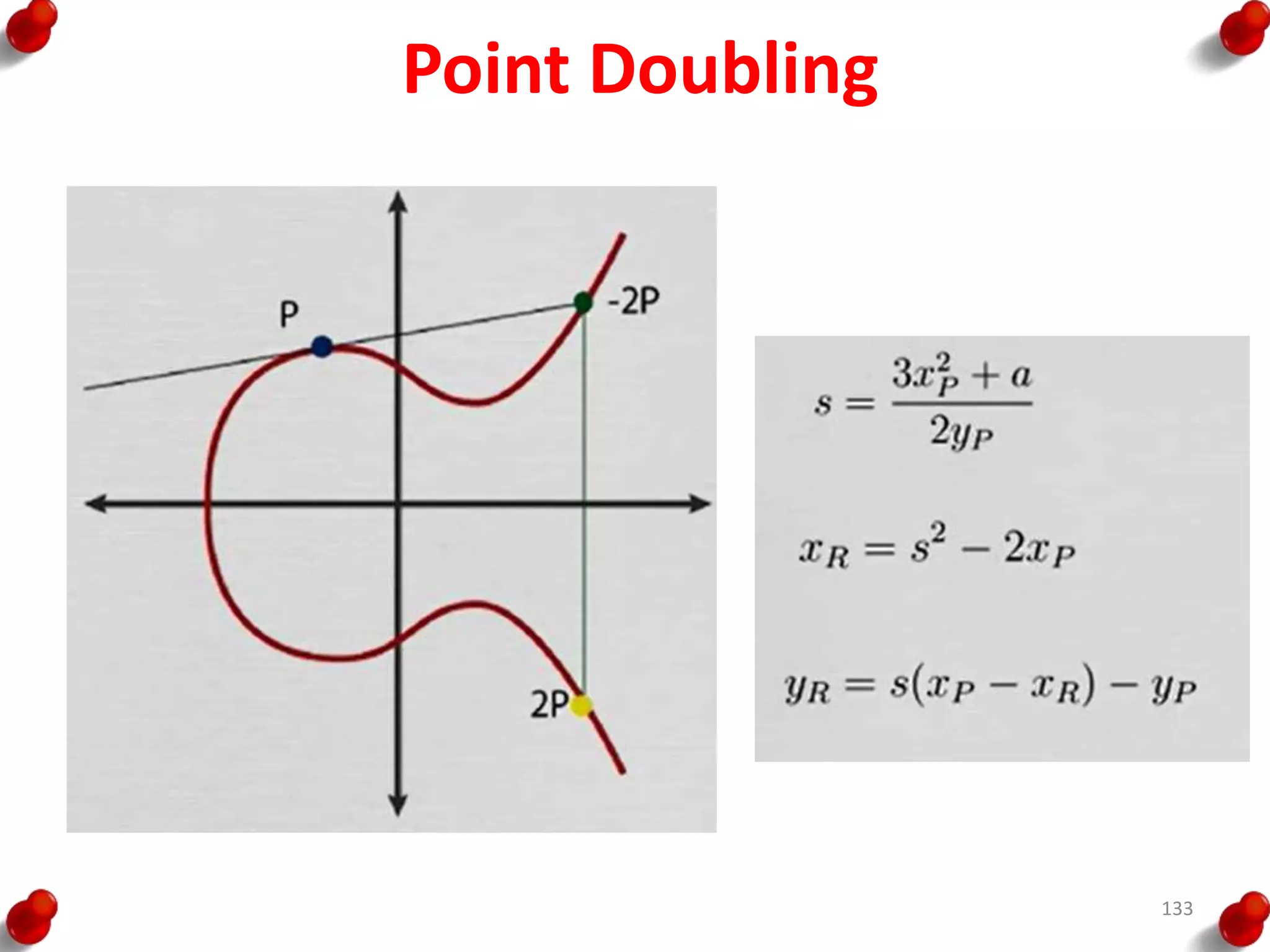
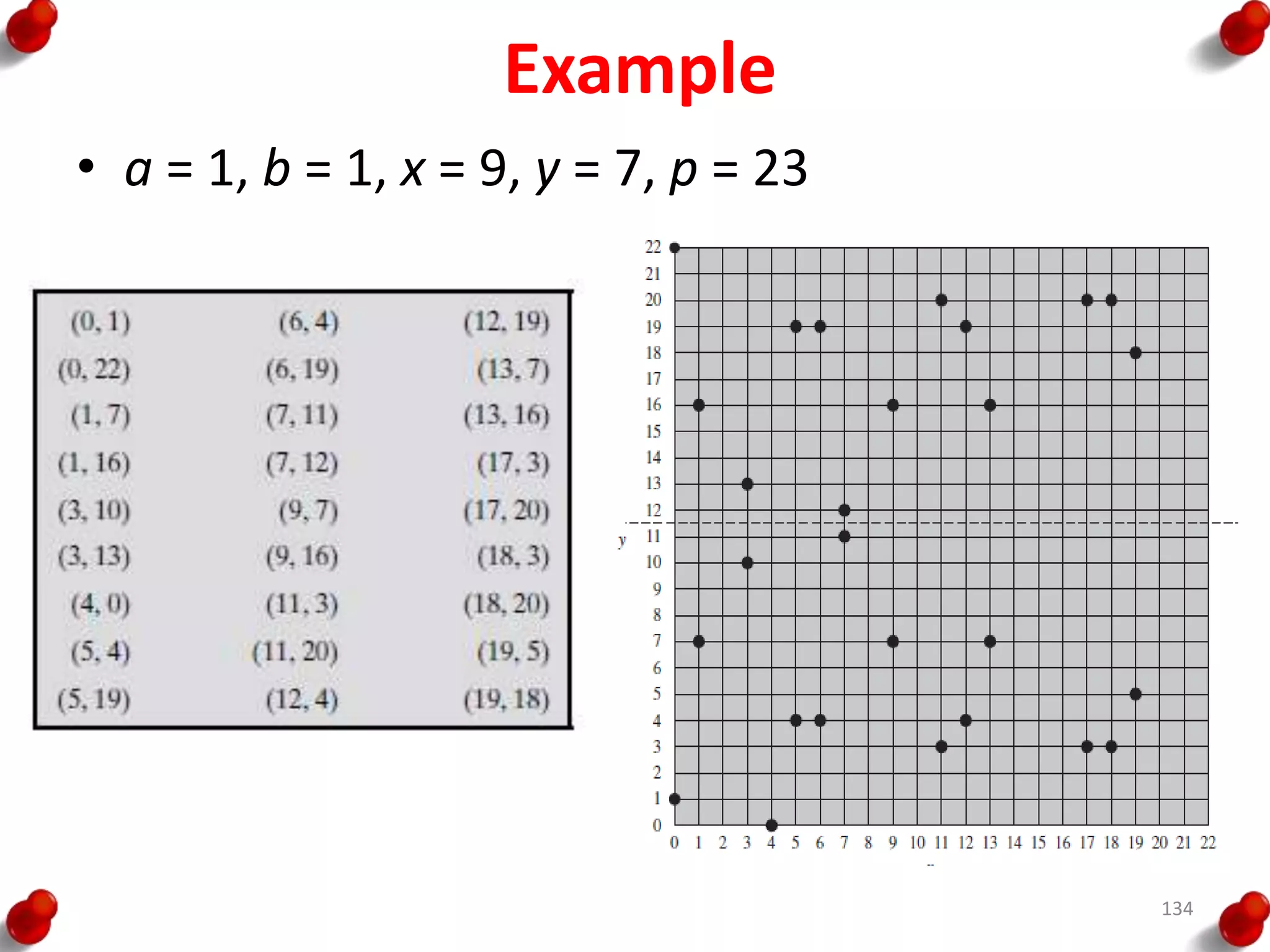
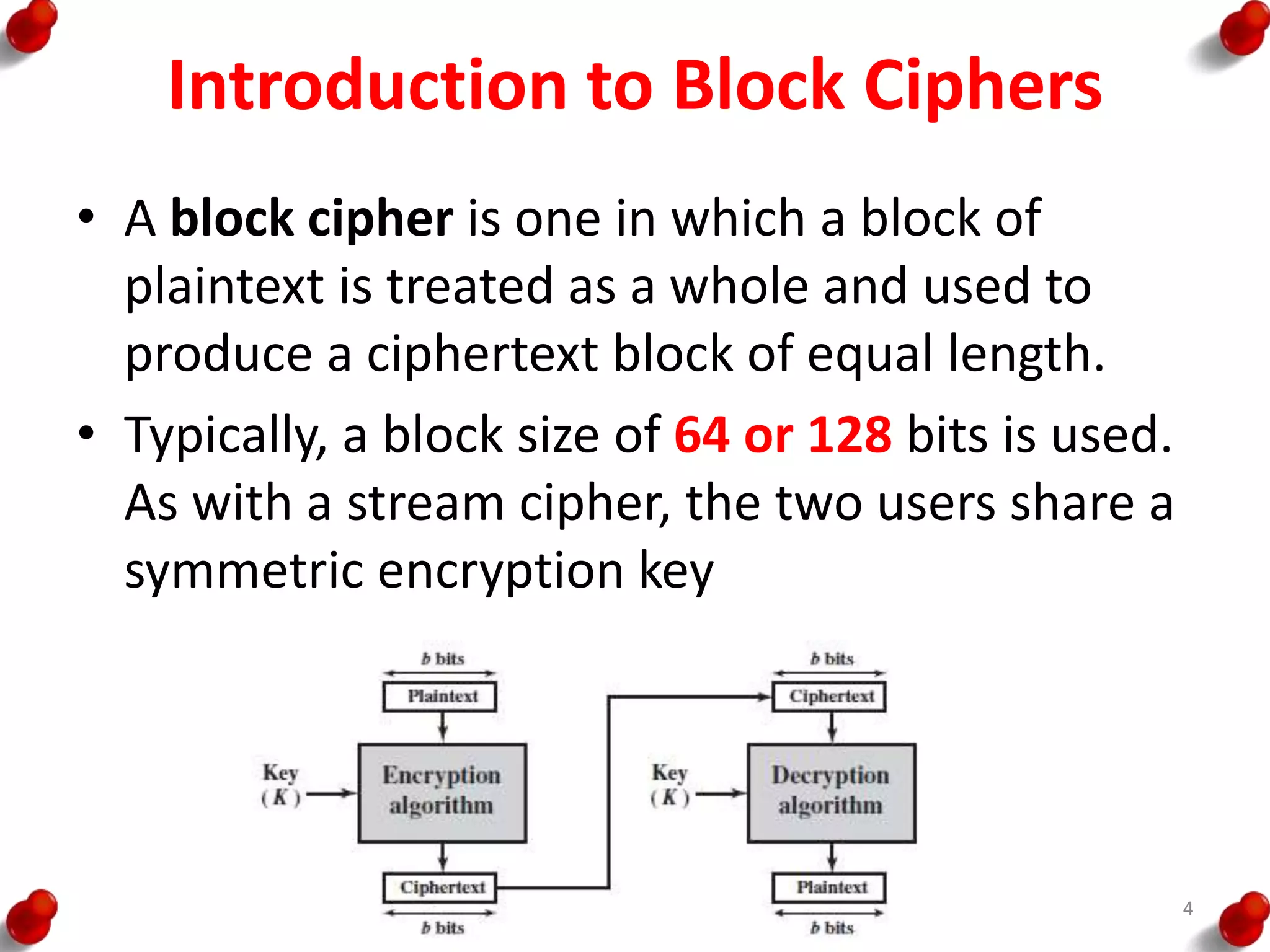
This document provides an overview of block ciphers and public key cryptography. It discusses the principles of block ciphers, including block cipher modes of operation. Popular block ciphers like DES, AES, Triple DES and Blowfish are described. The document also covers public key cryptography principles and algorithms like RSA and Diffie-Hellman key exchange. It provides details on elliptic curve cryptography and the arithmetic behind it.














![DES - Encryption
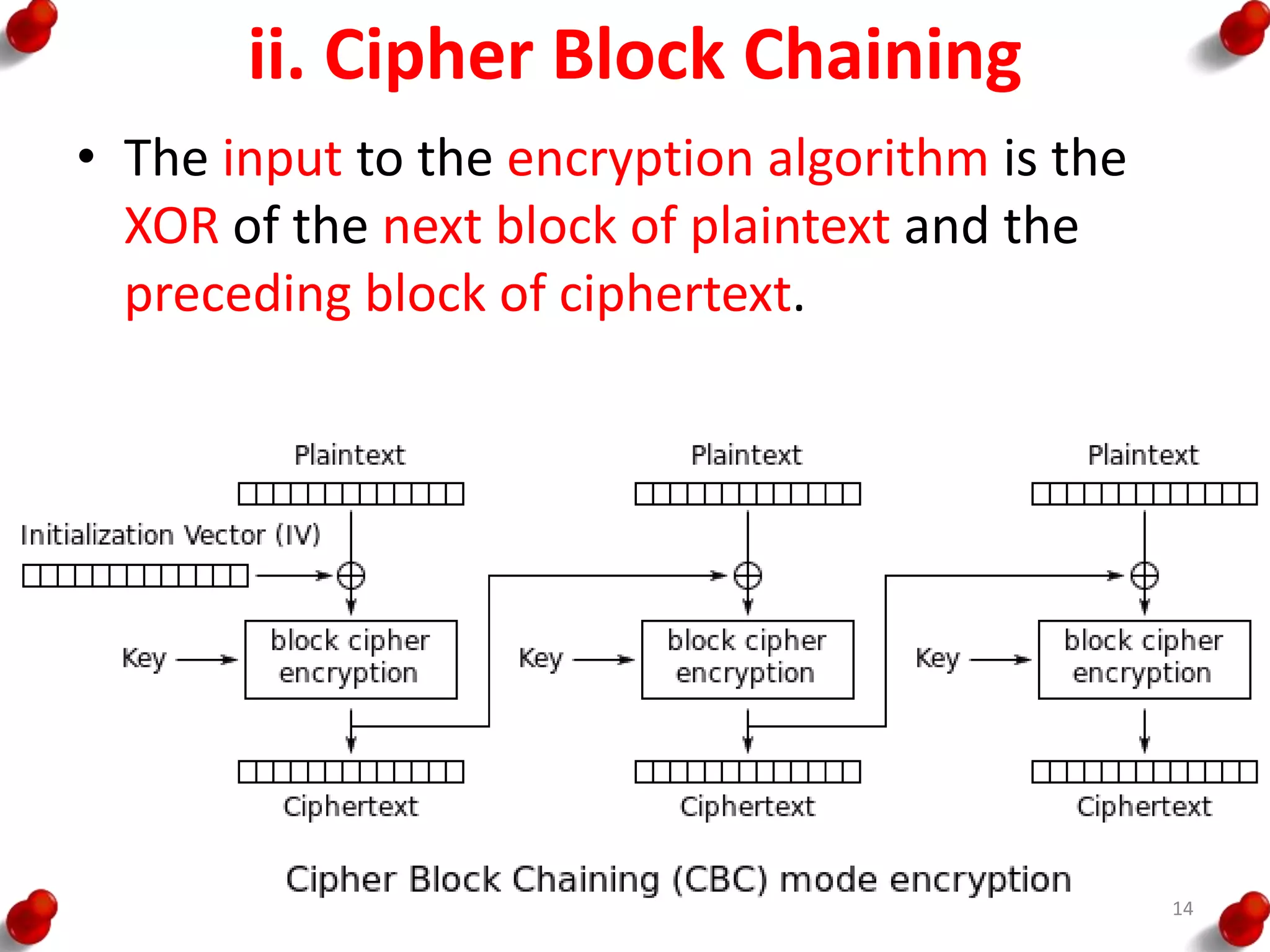
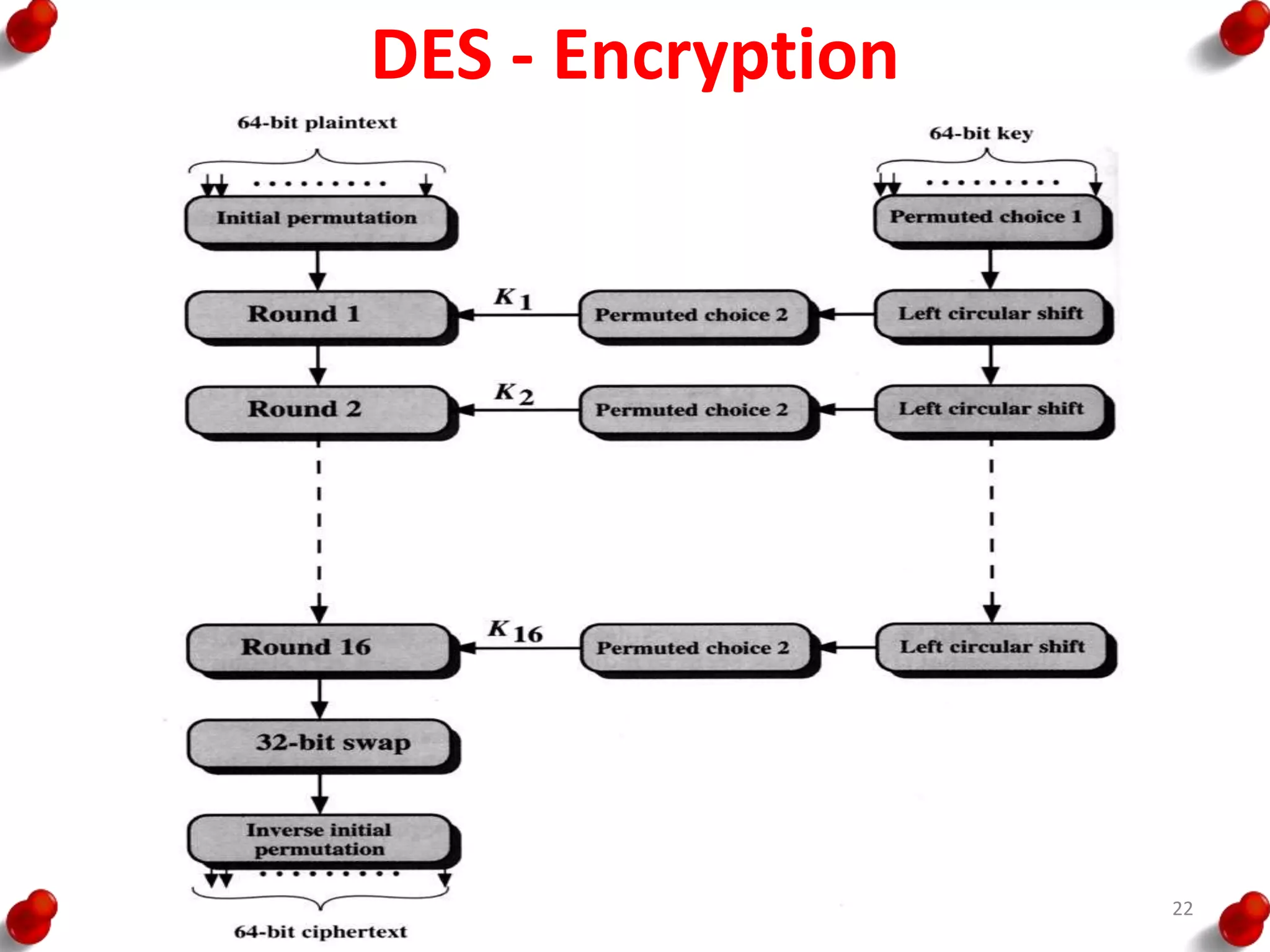
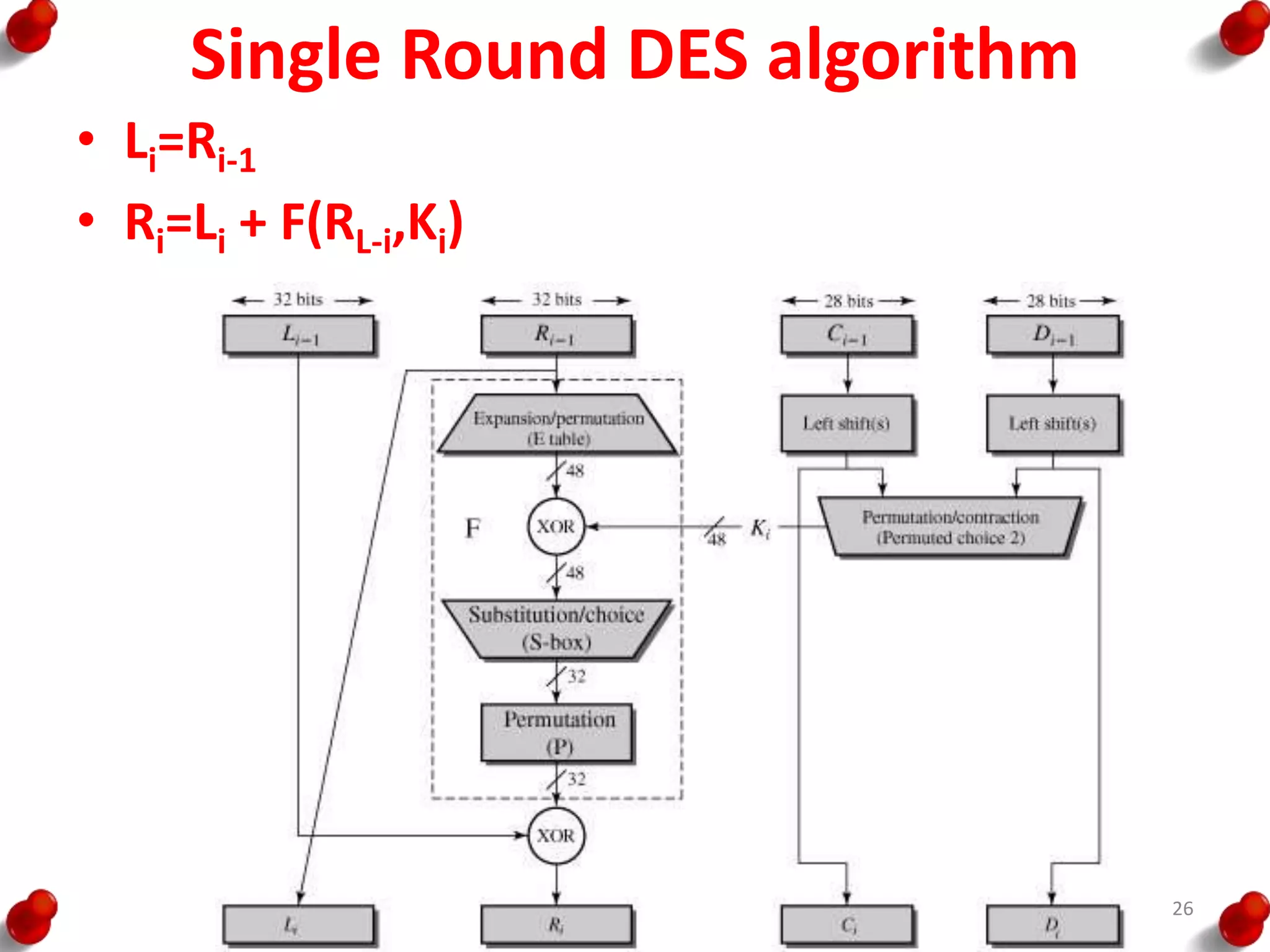
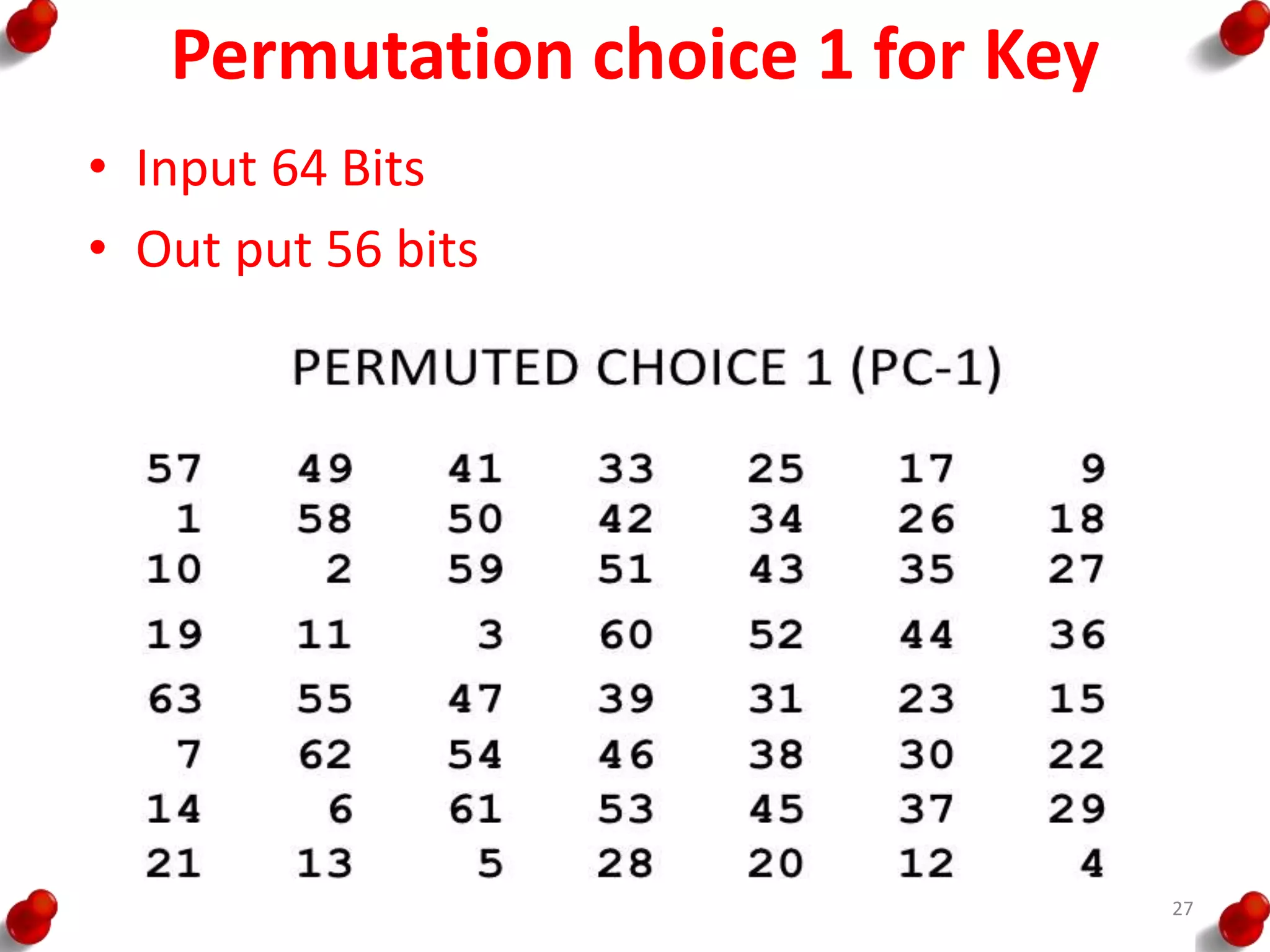
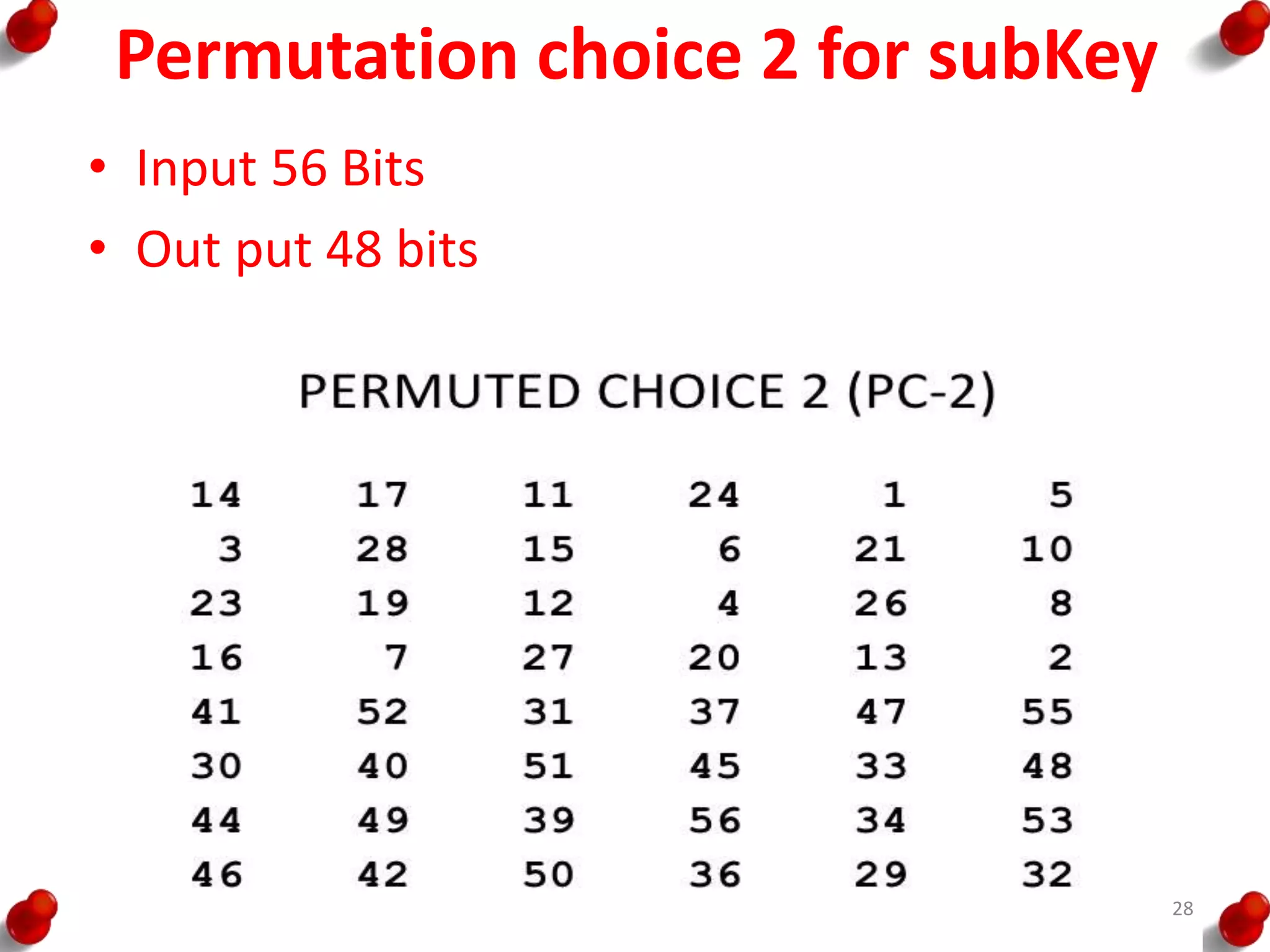
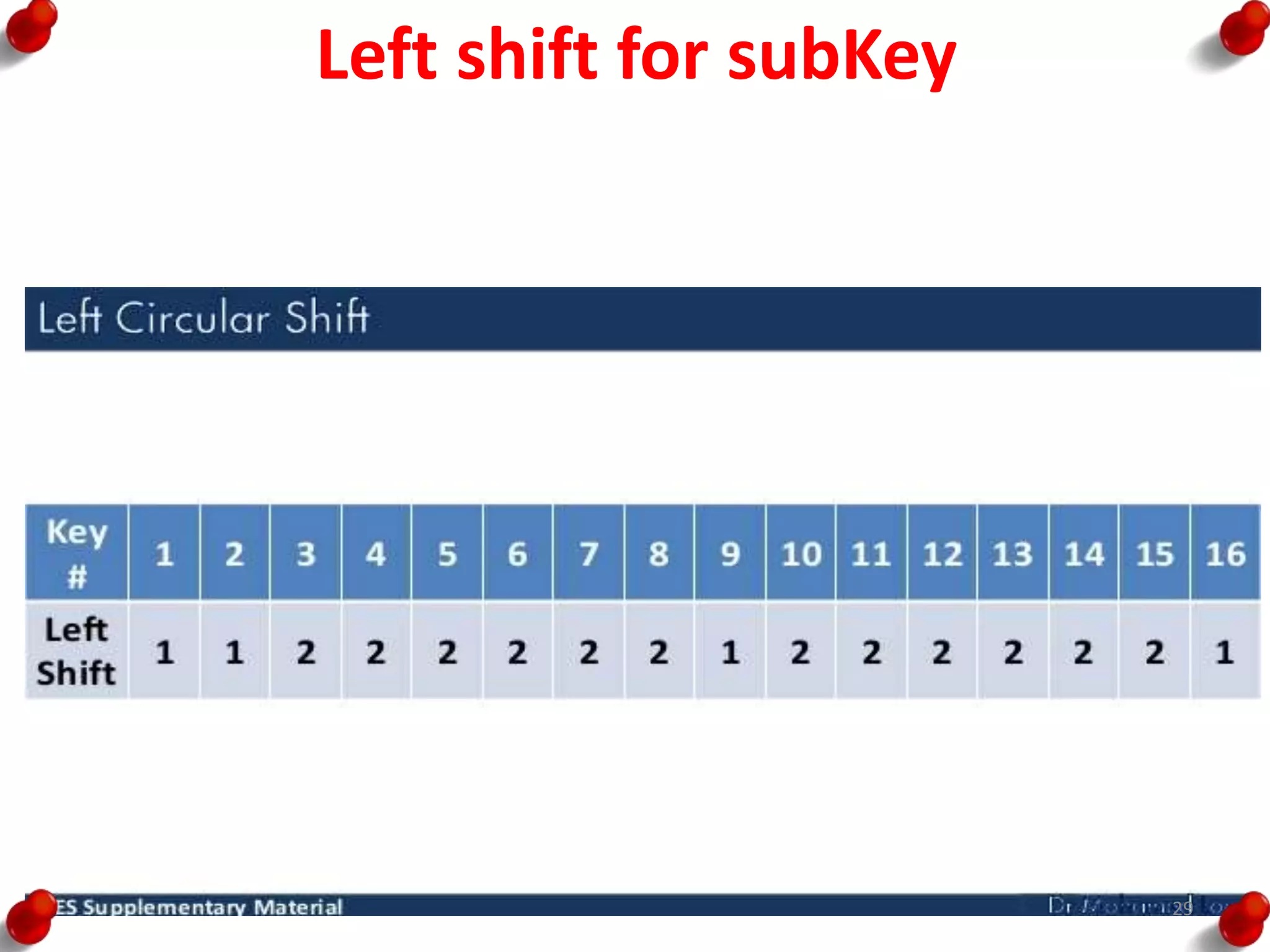
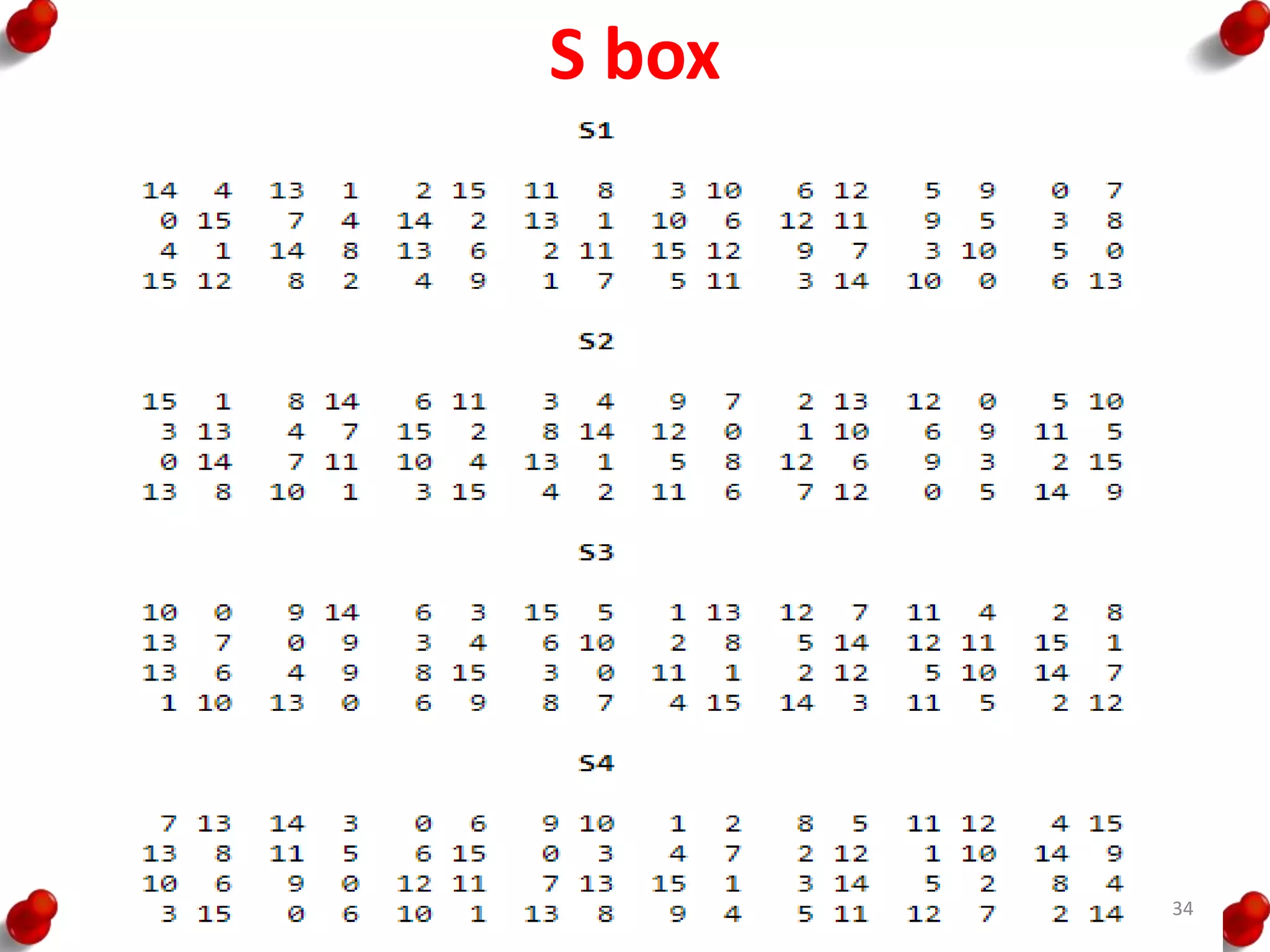
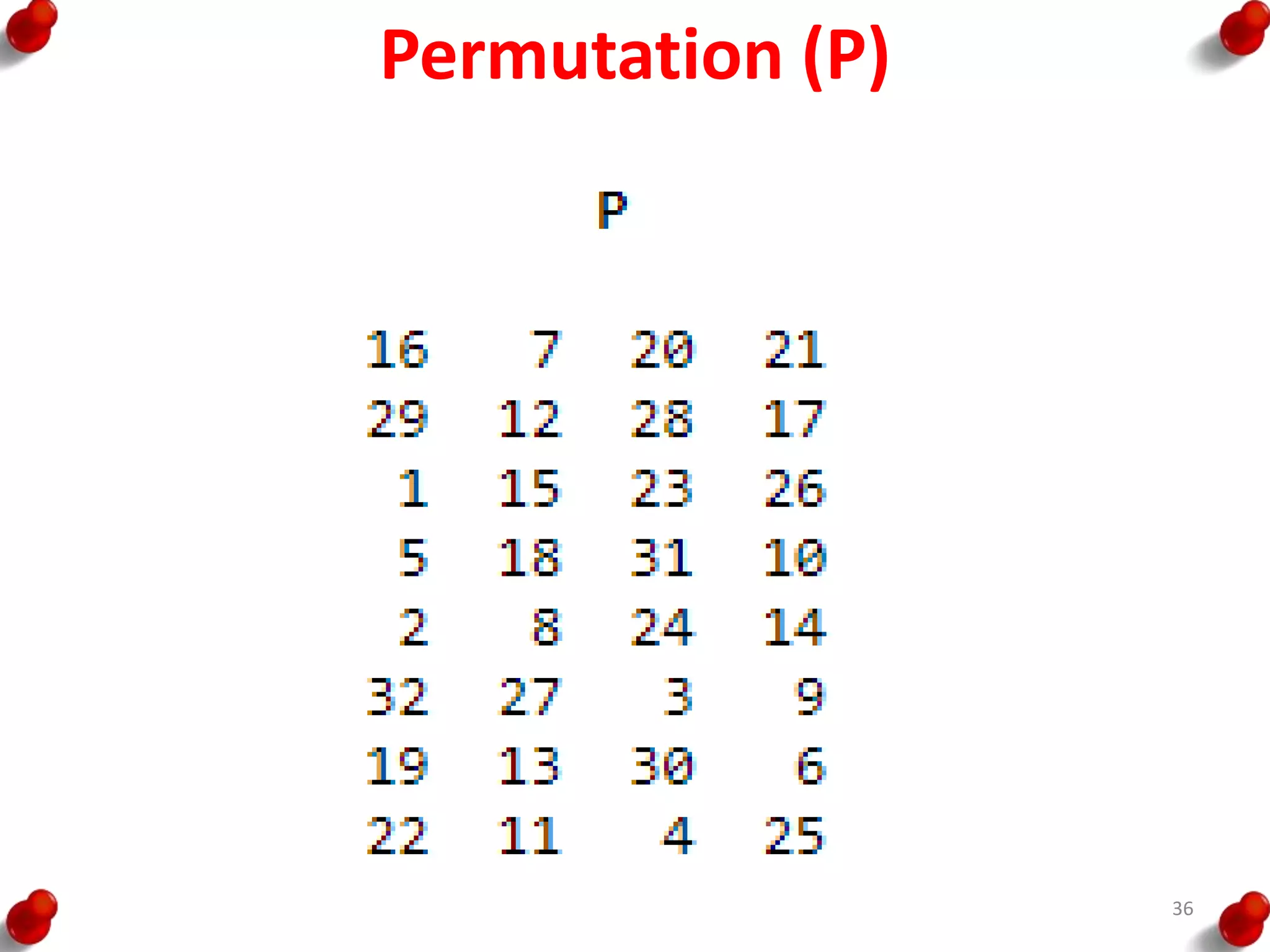
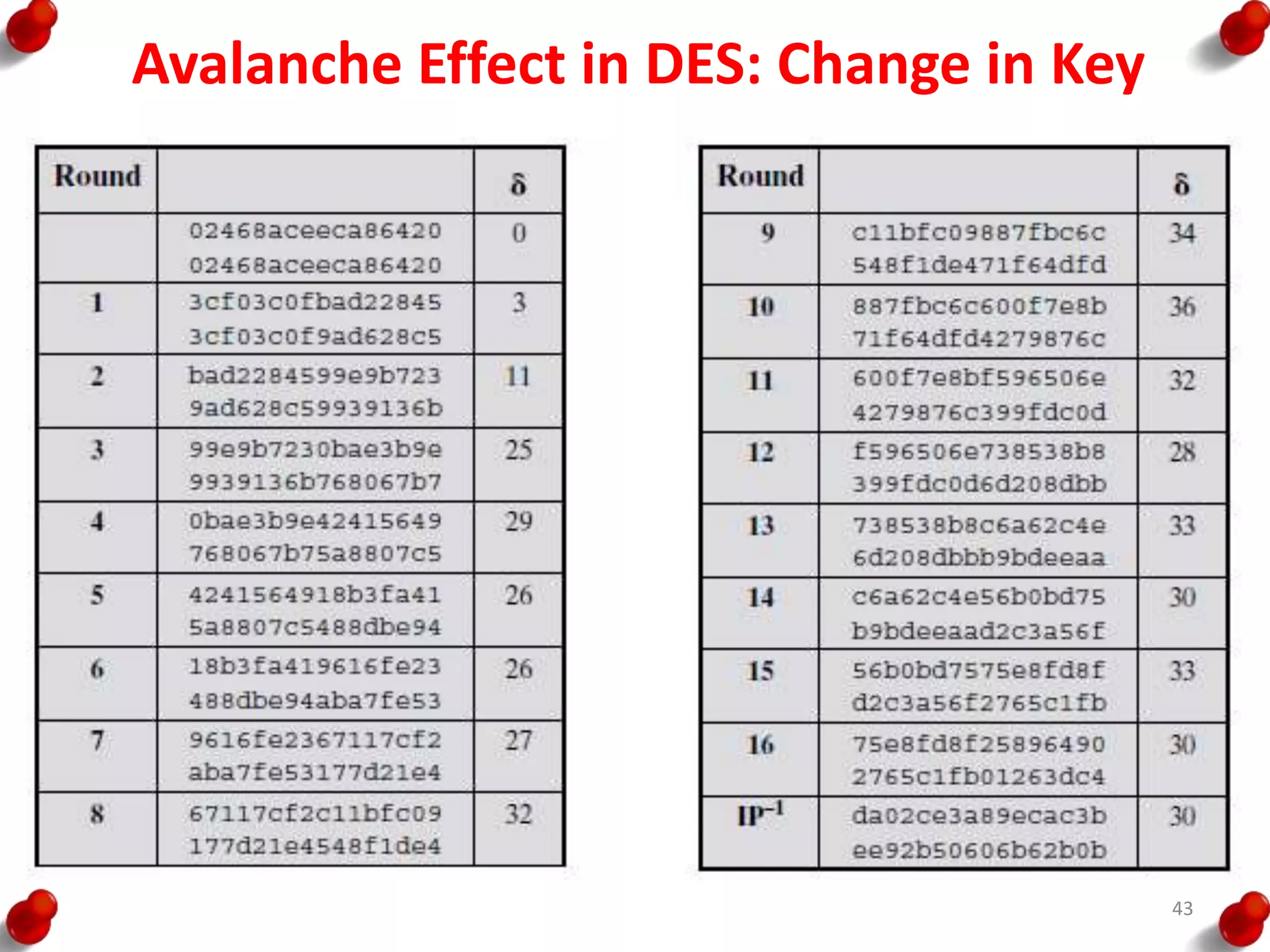
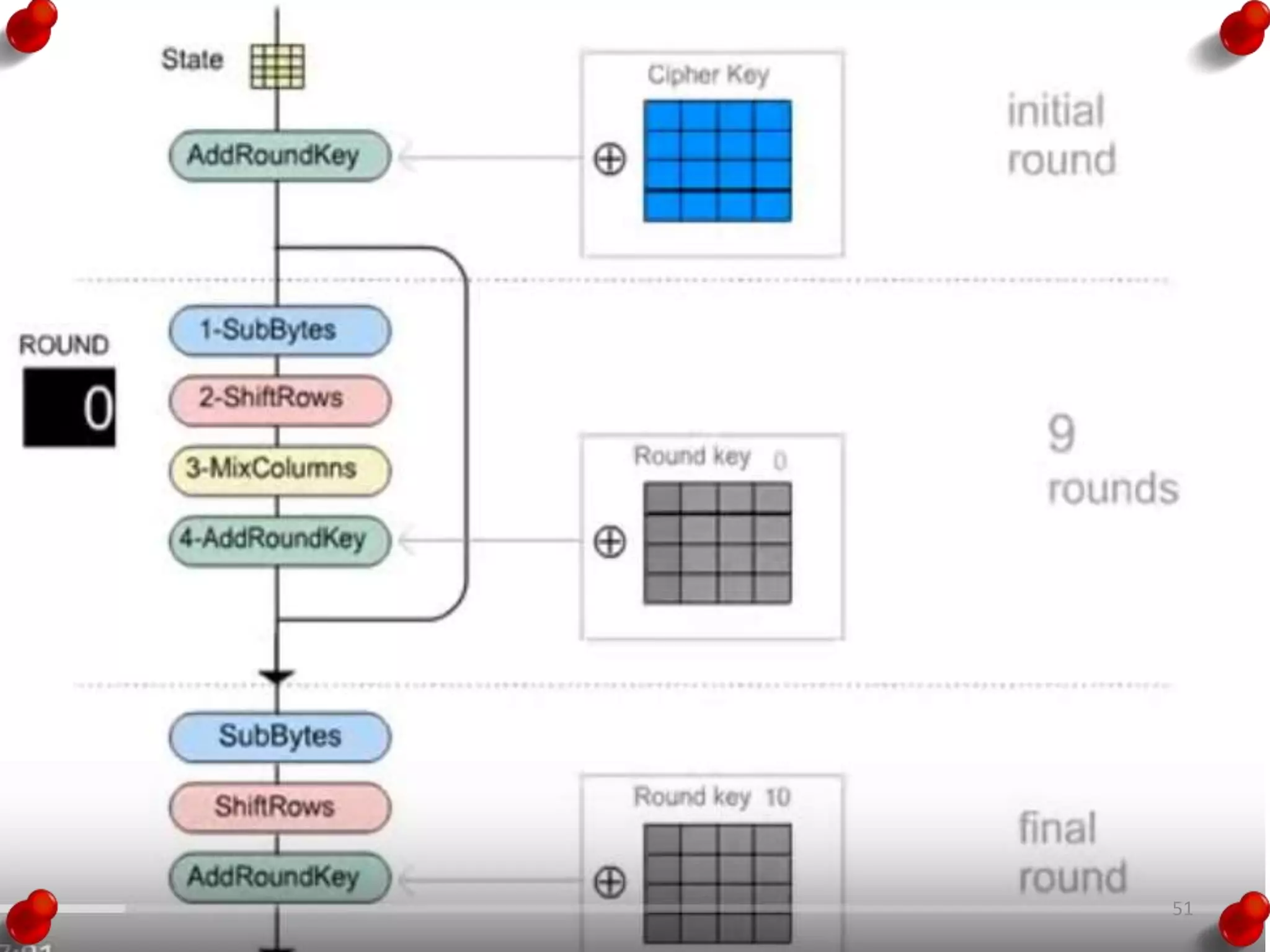
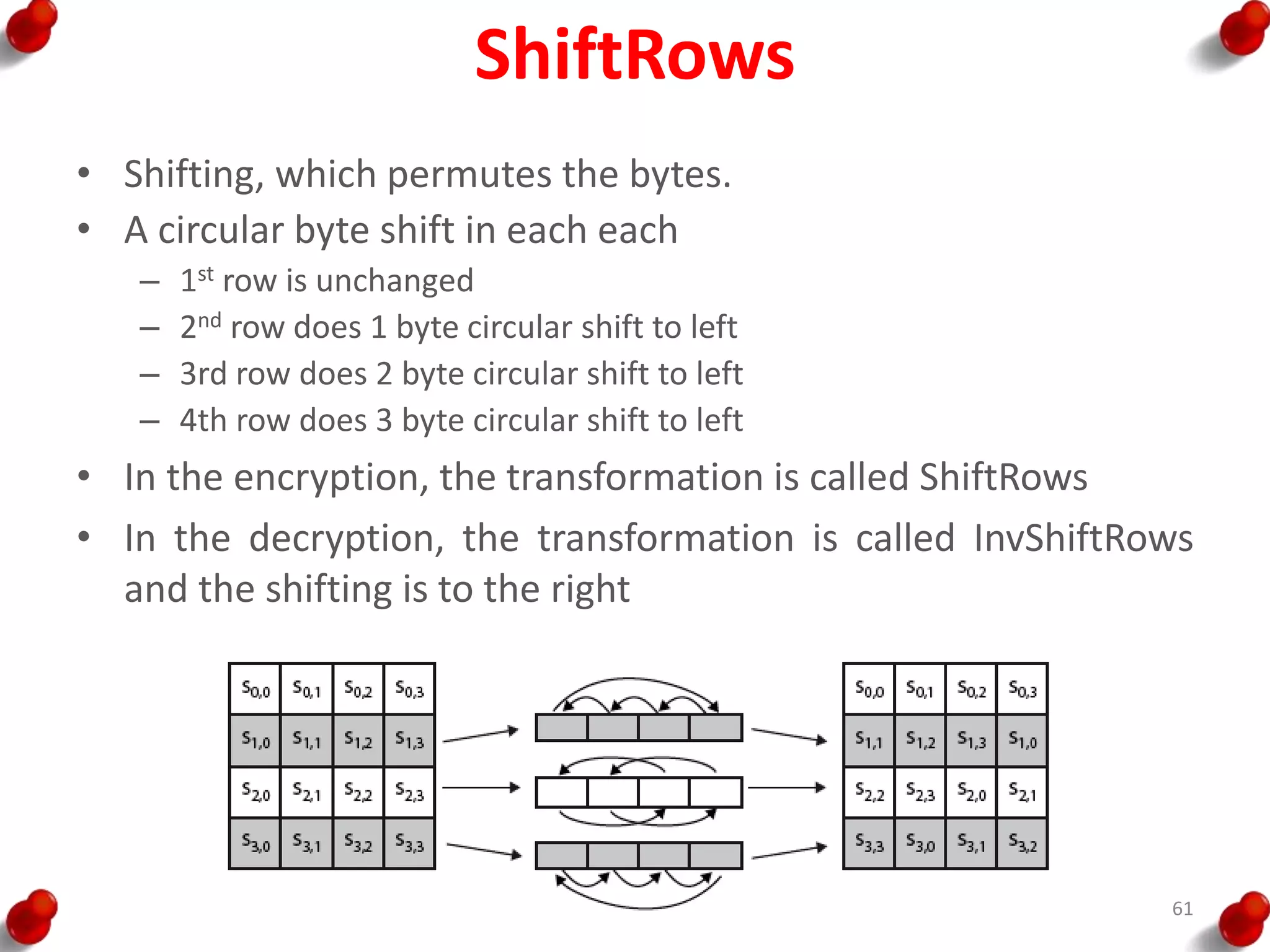
• Processing of the plaintext proceeds in three phases.
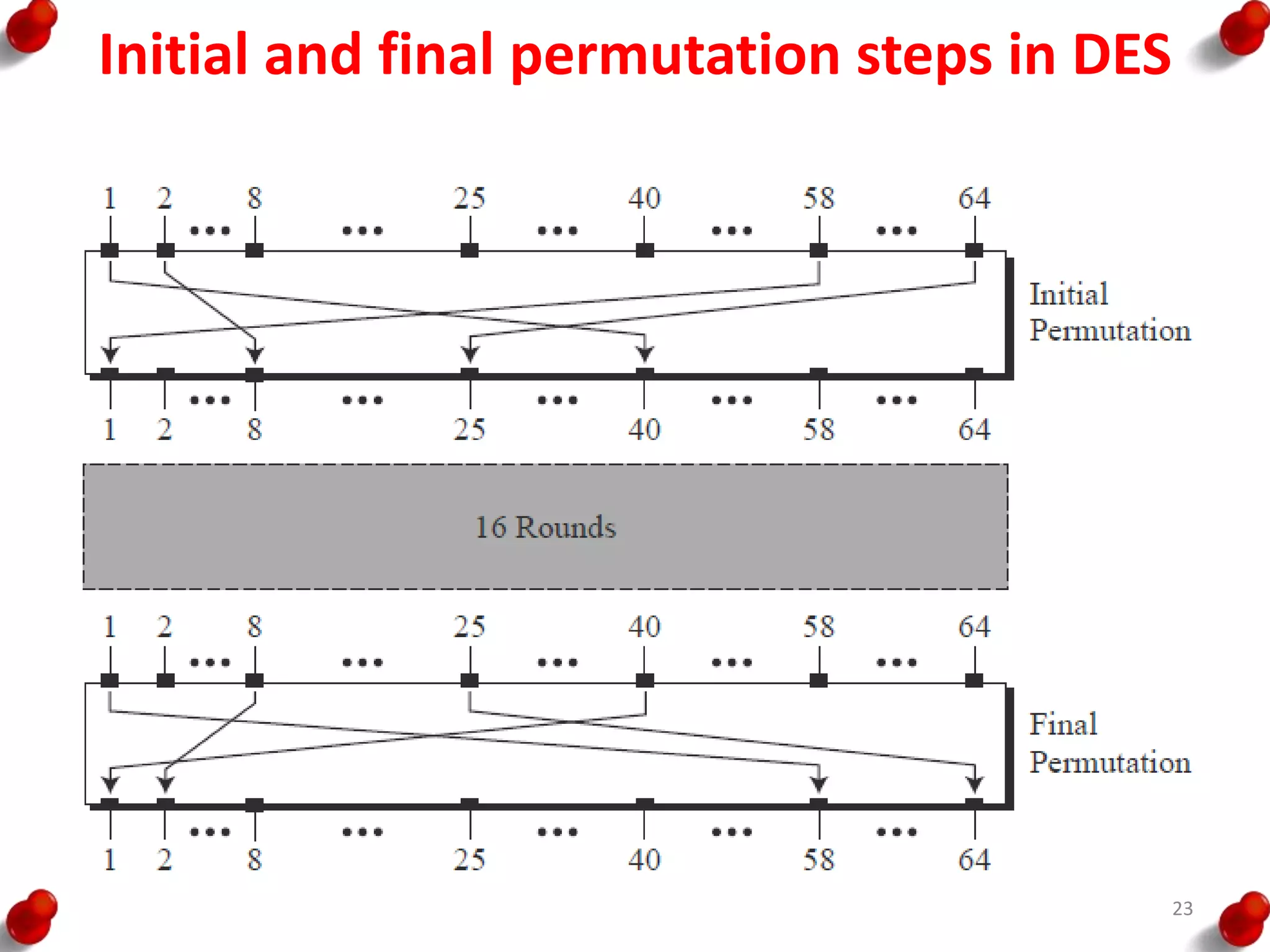
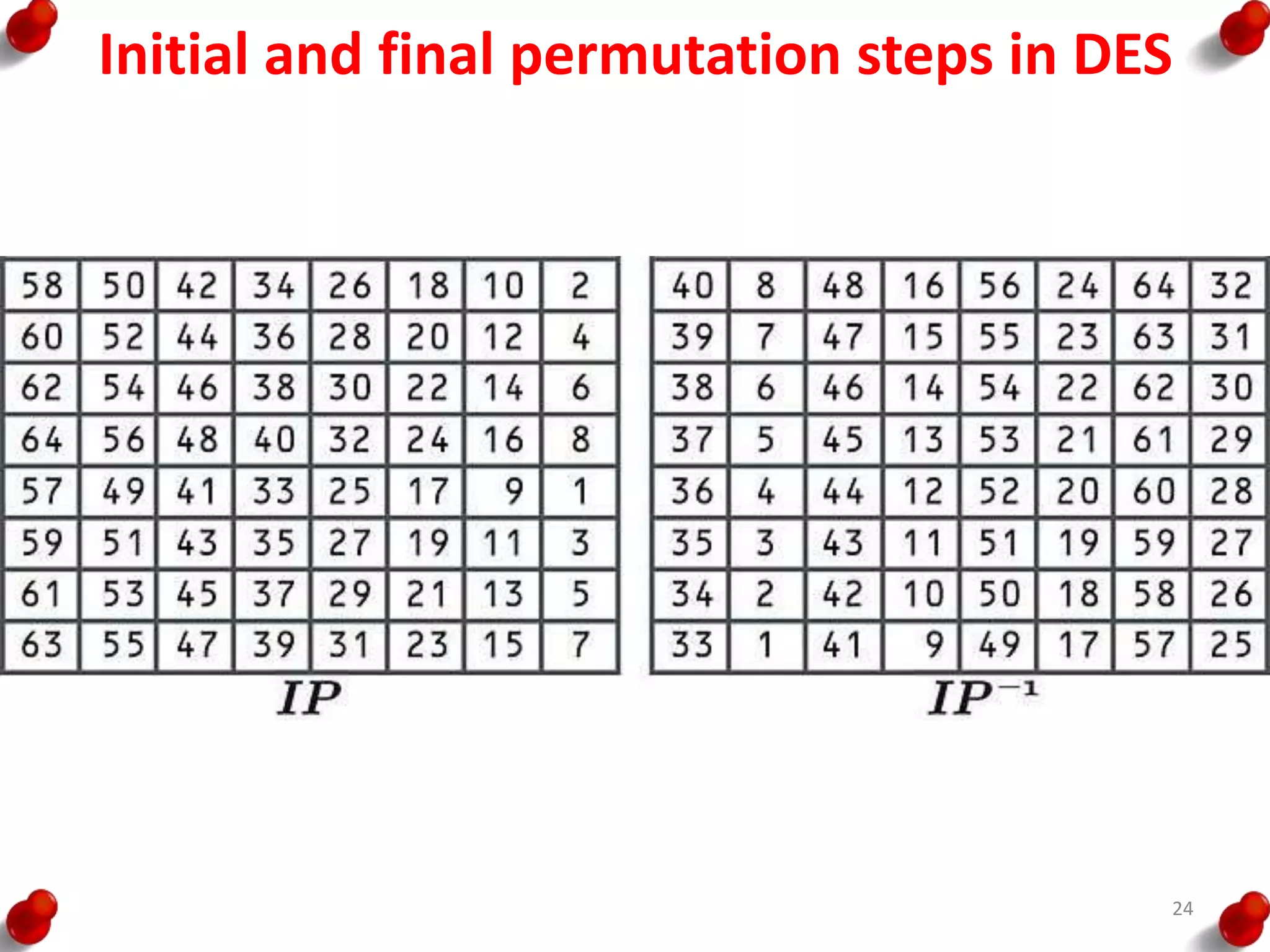
– First, the 64-bit plaintext passes through an initial
permutation (IP) that rearranges the bits to produce the
permuted input.
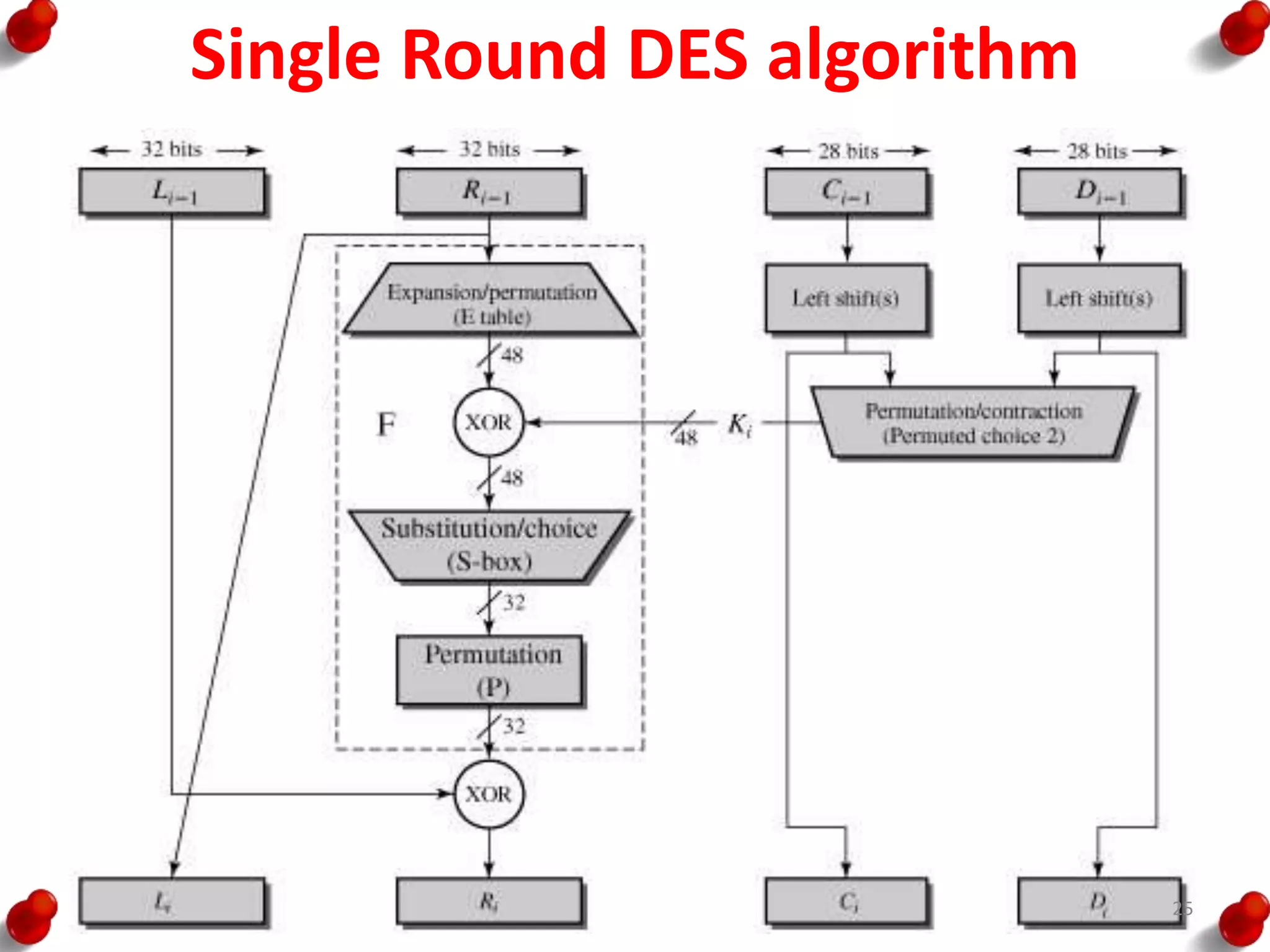
– This is followed by a phase consisting of sixteen rounds of
the same function, which involves both permutation and
substitution functions.
– The output of the last (sixteenth) round consists of 64 bits
that are a function of the input plaintext and the key.
– The left and right halves of the output are swapped to
produce the pre output.
– Finally, the preoutput is passed through a permutation
[IP -1] that is the inverse of the initial permutation function,
to produce the 64-bit ciphertext.
38](https://image.slidesharecdn.com/blockcipherspublickeycryptography-190918102803/75/Block-ciphers-amp-public-key-cryptography-38-2048.jpg)






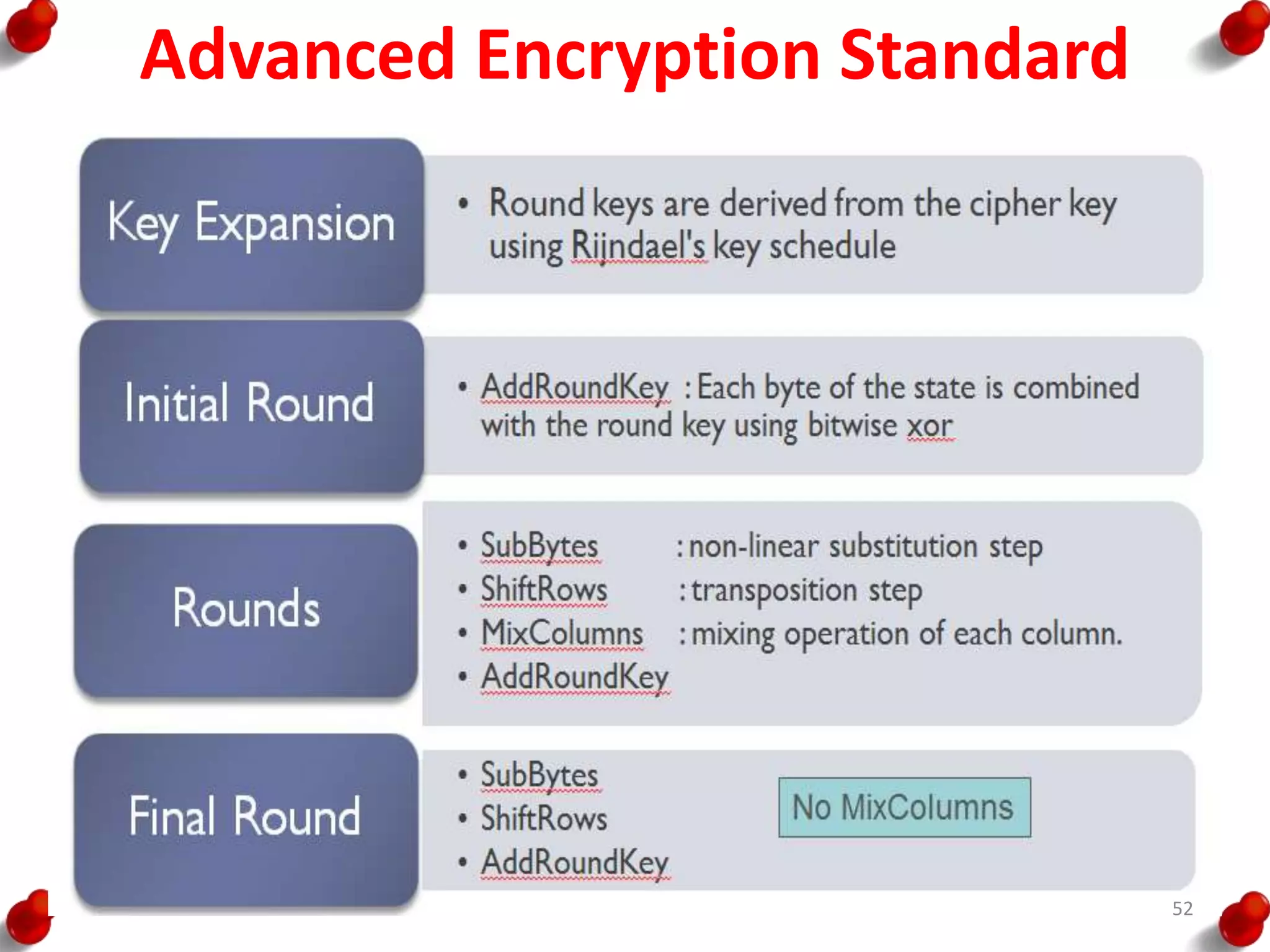
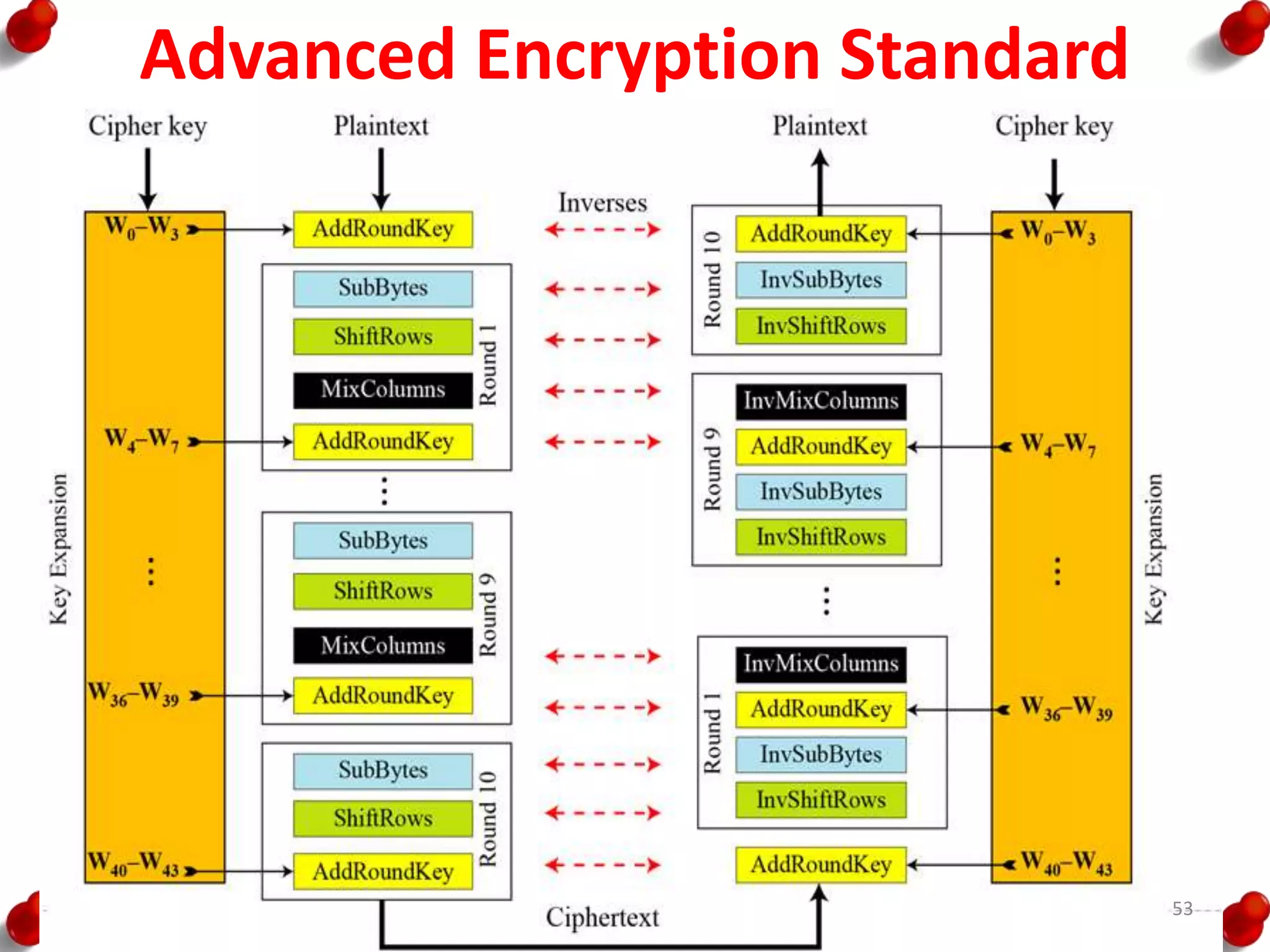

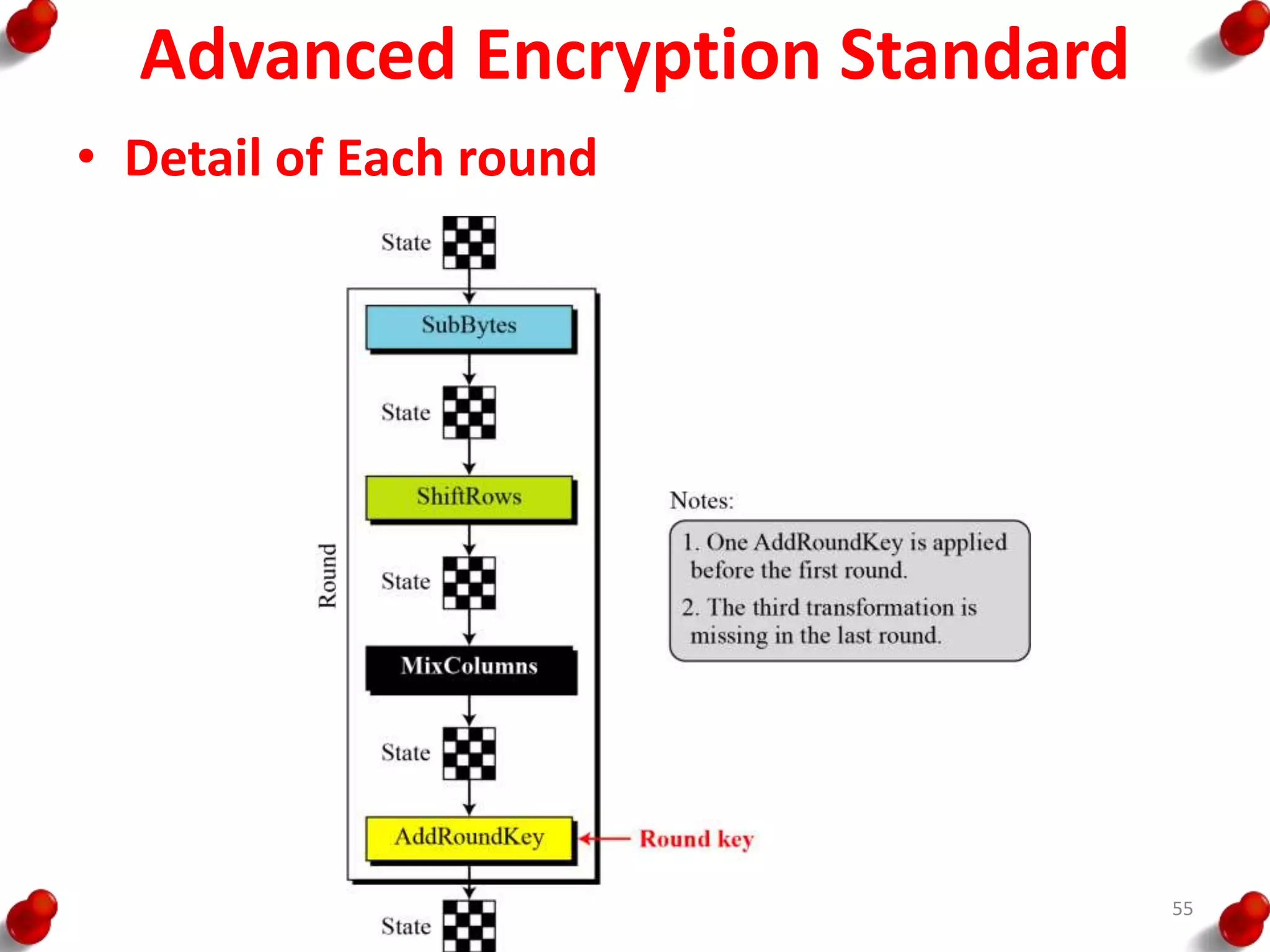

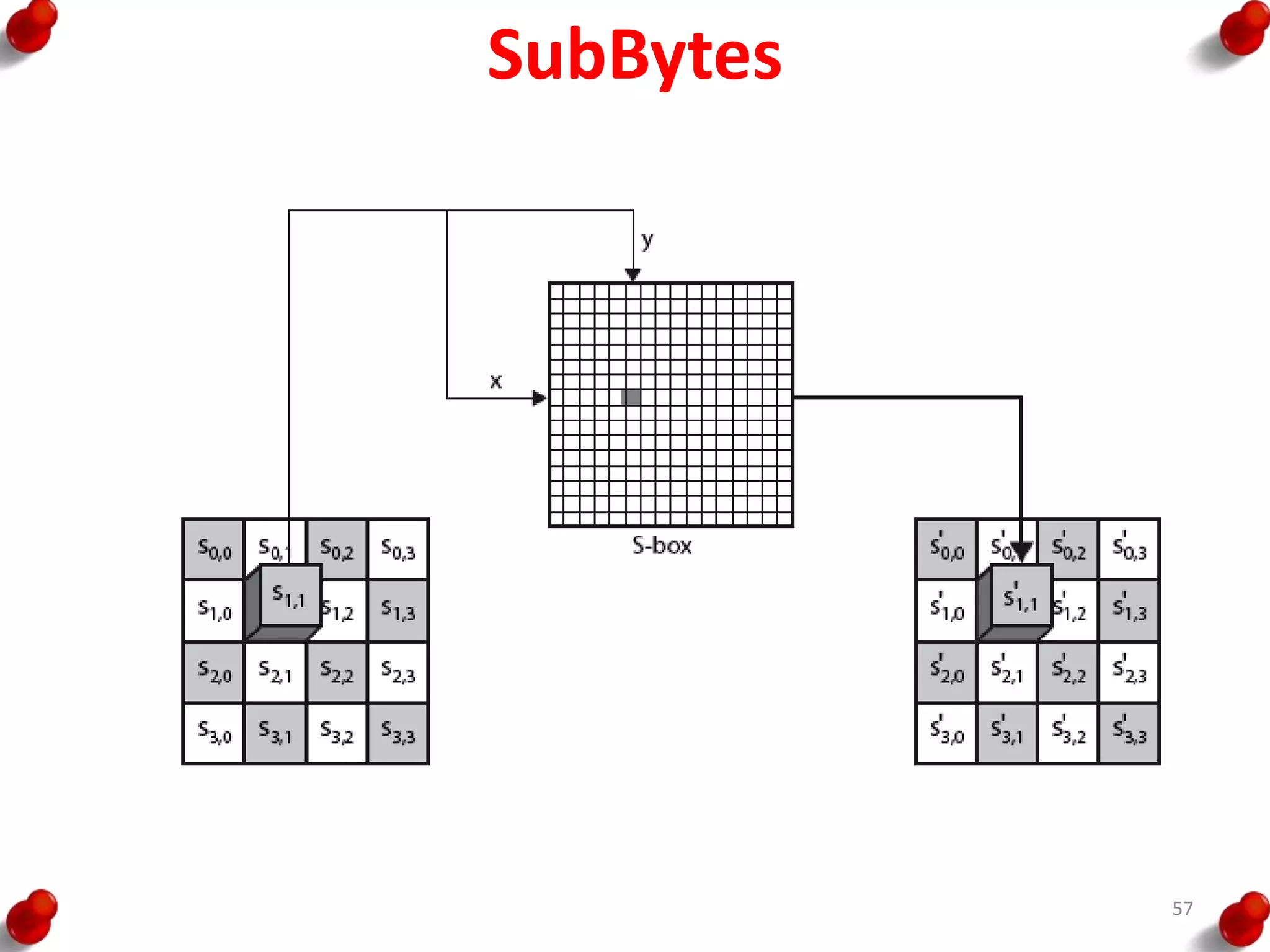
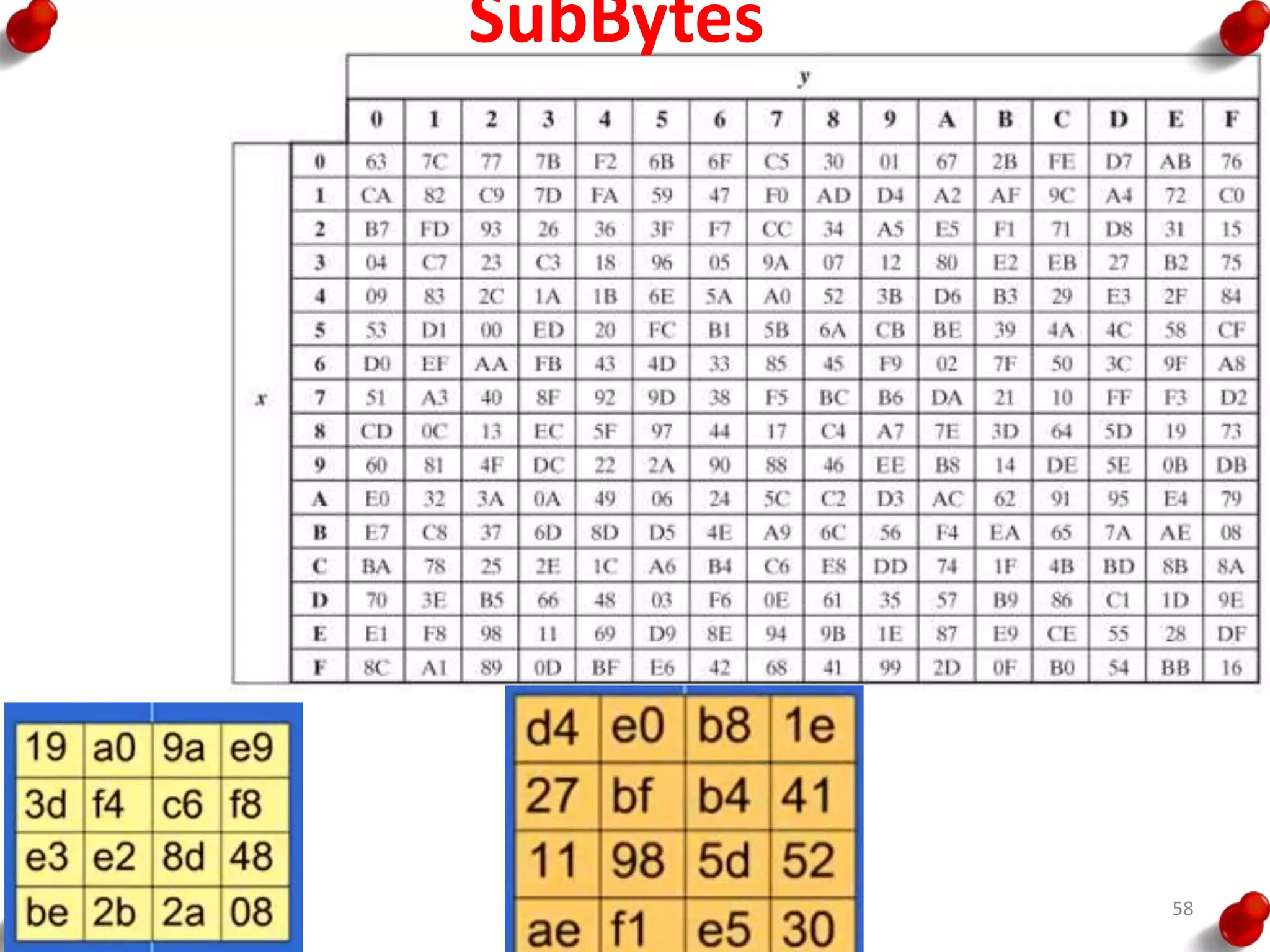
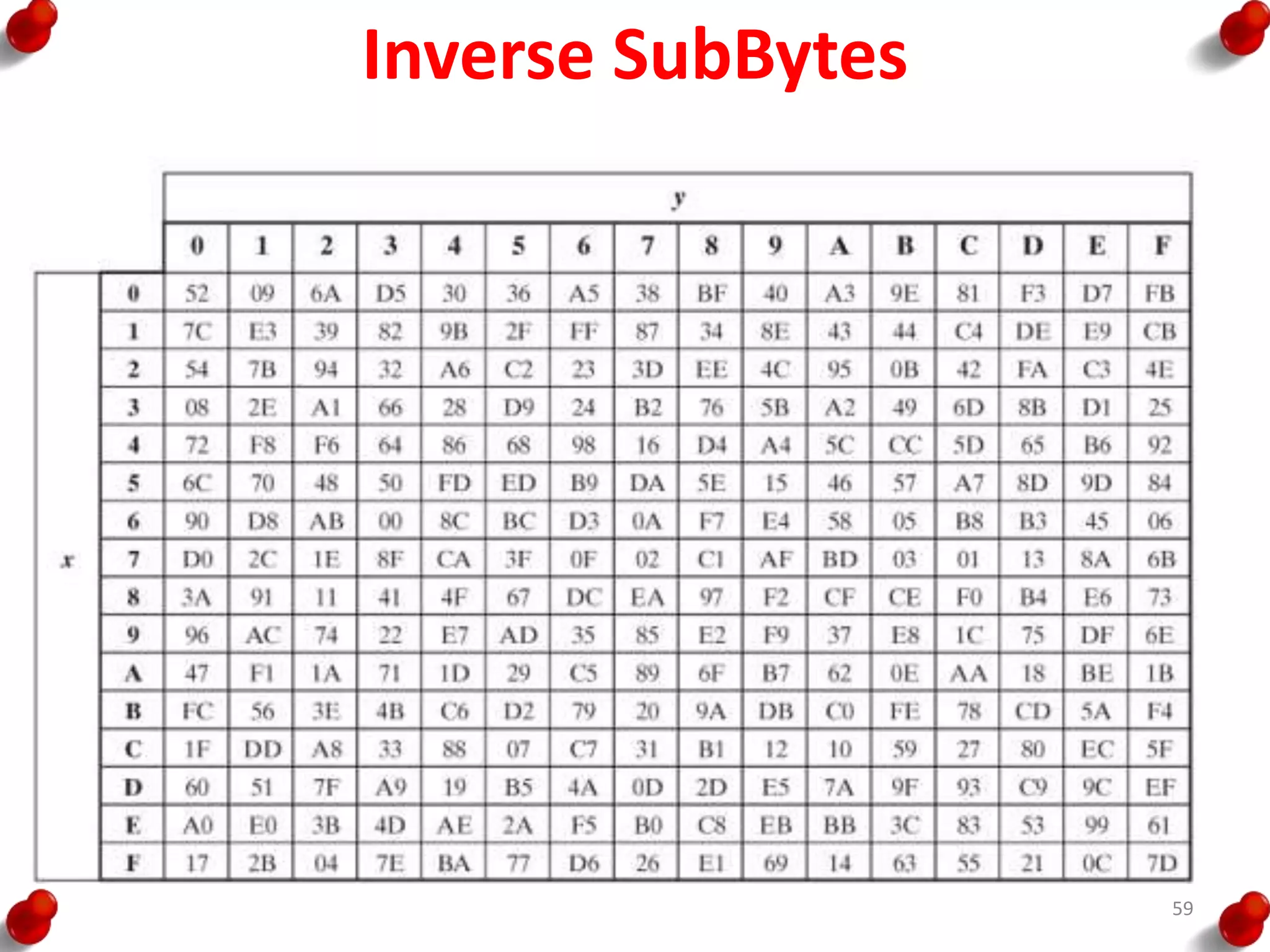
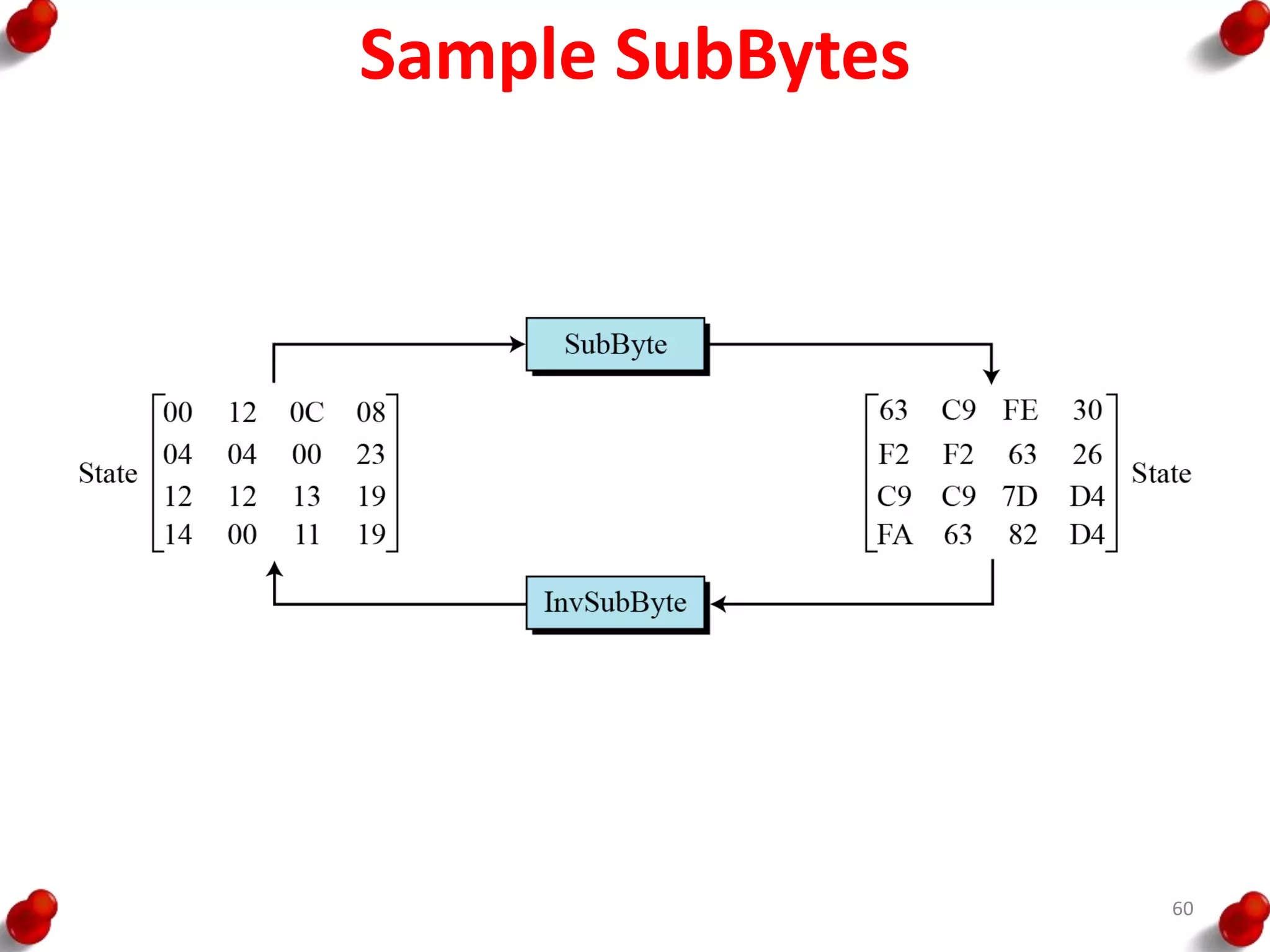
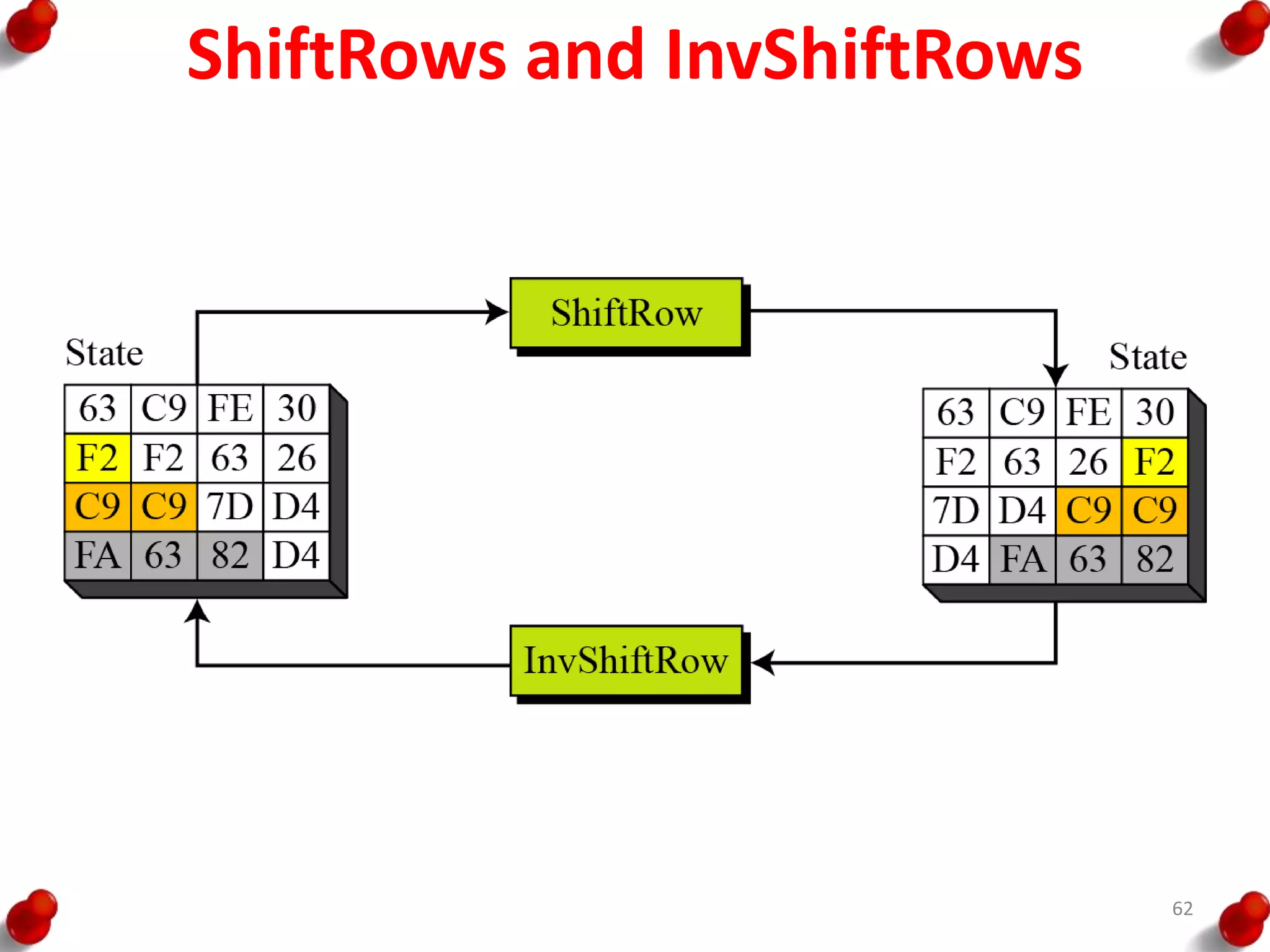

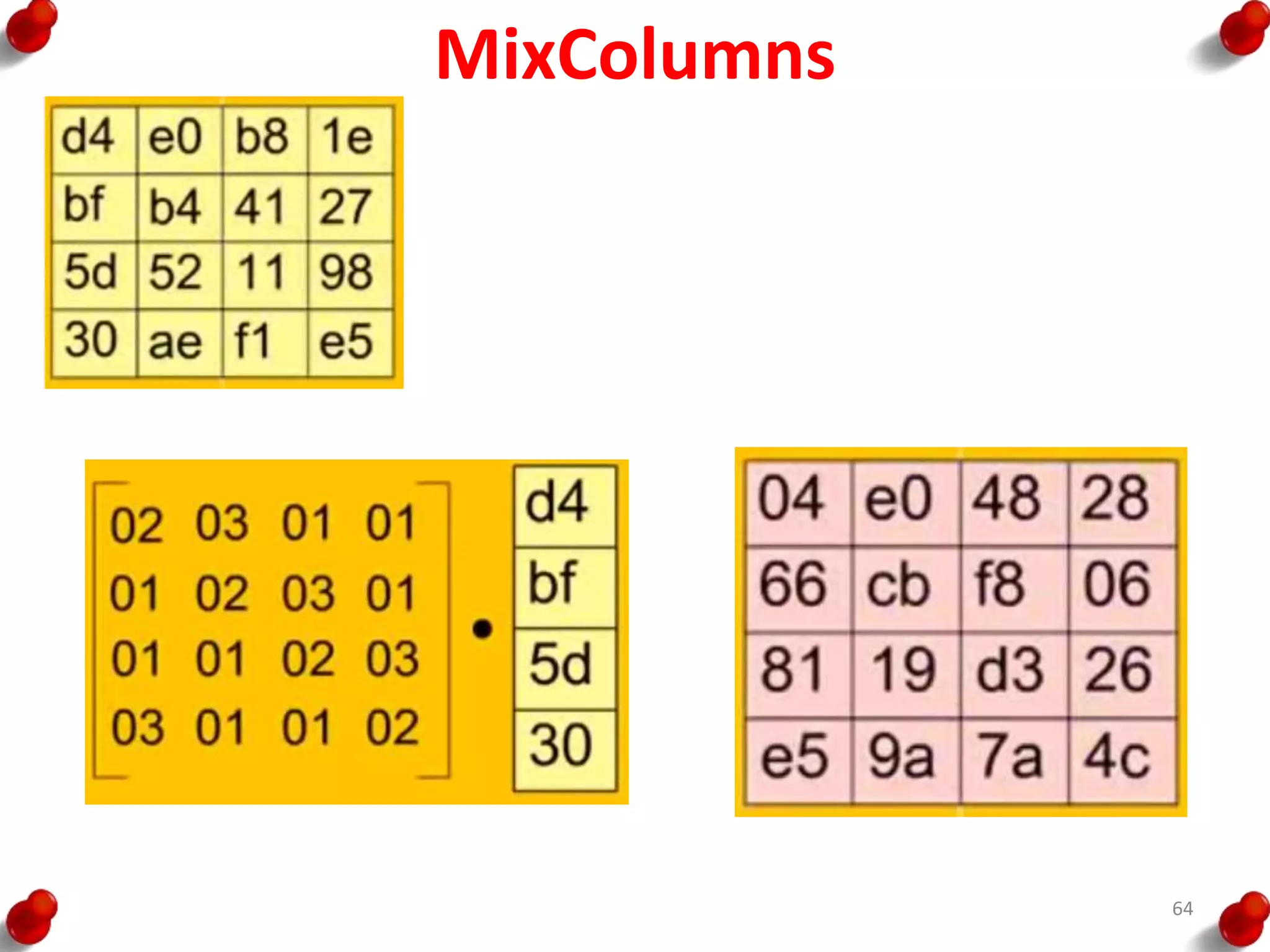

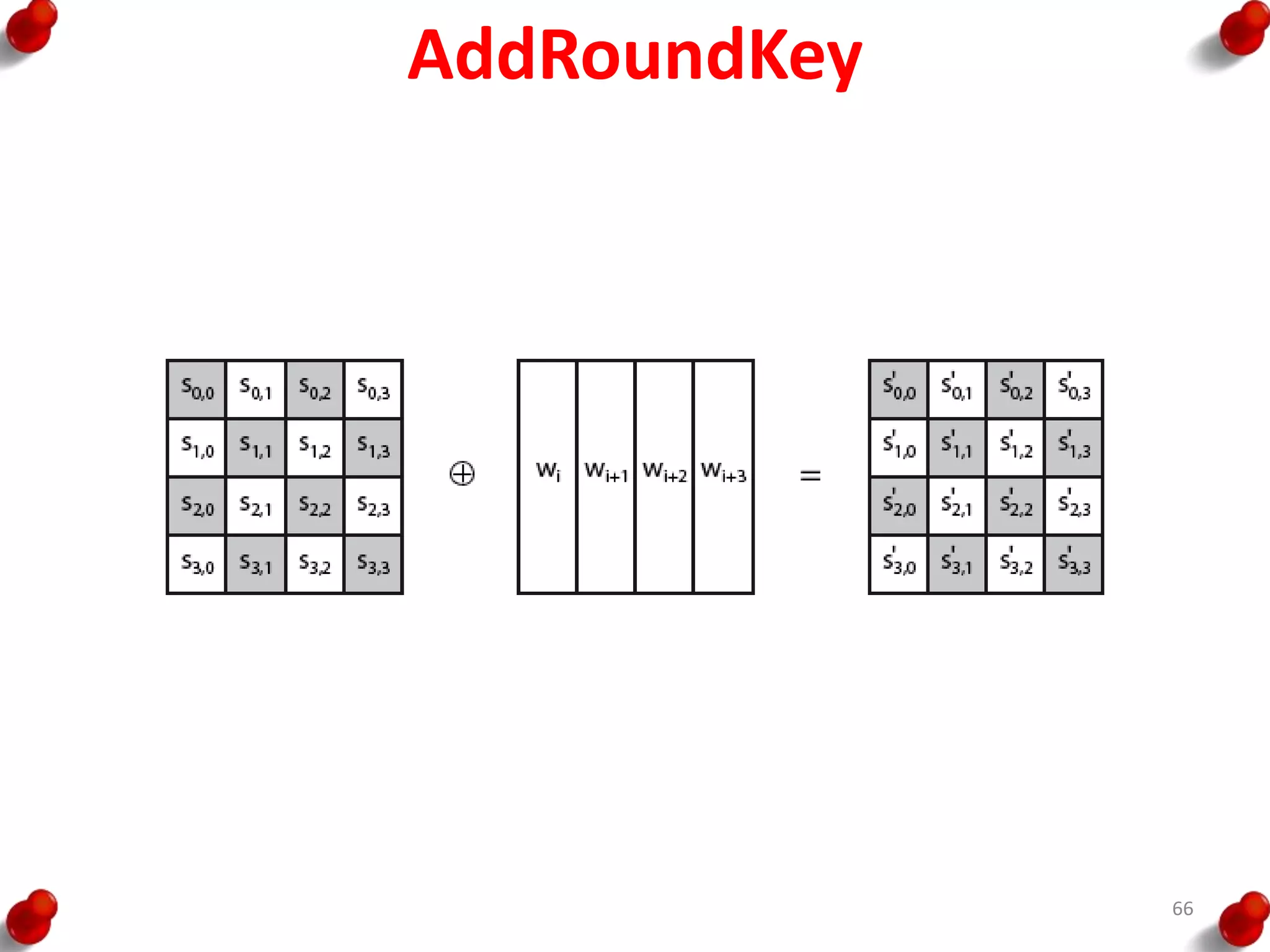
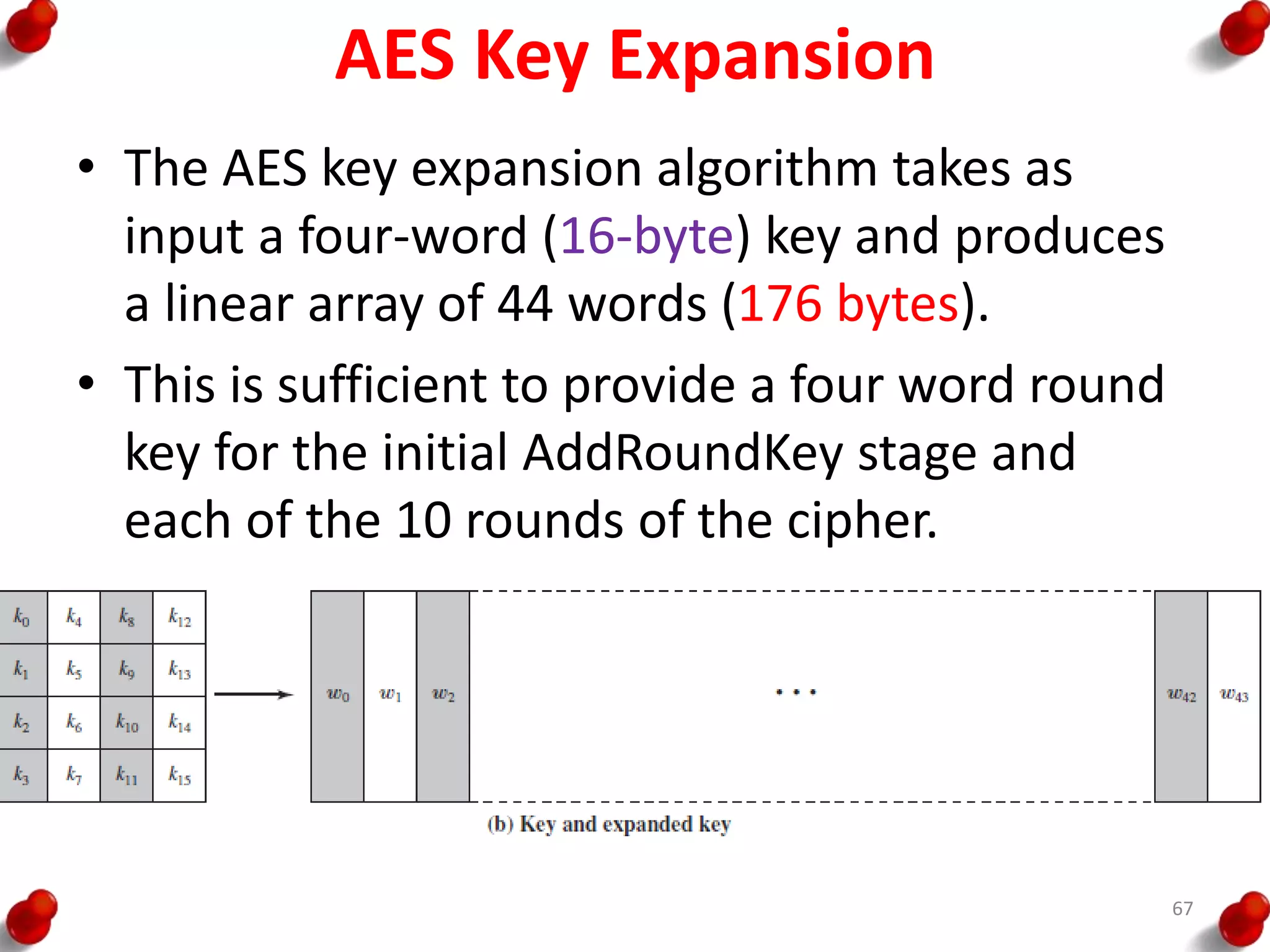
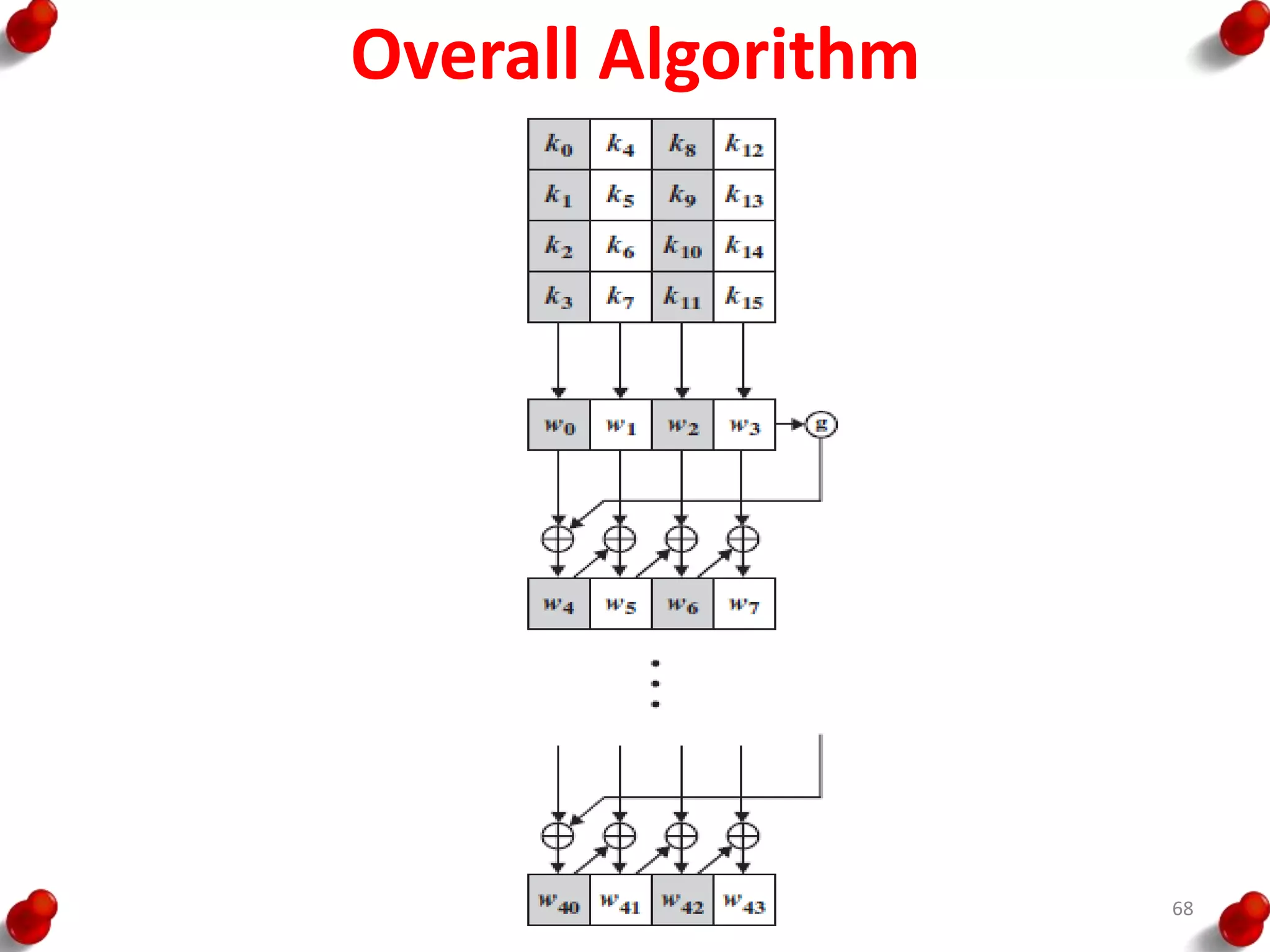
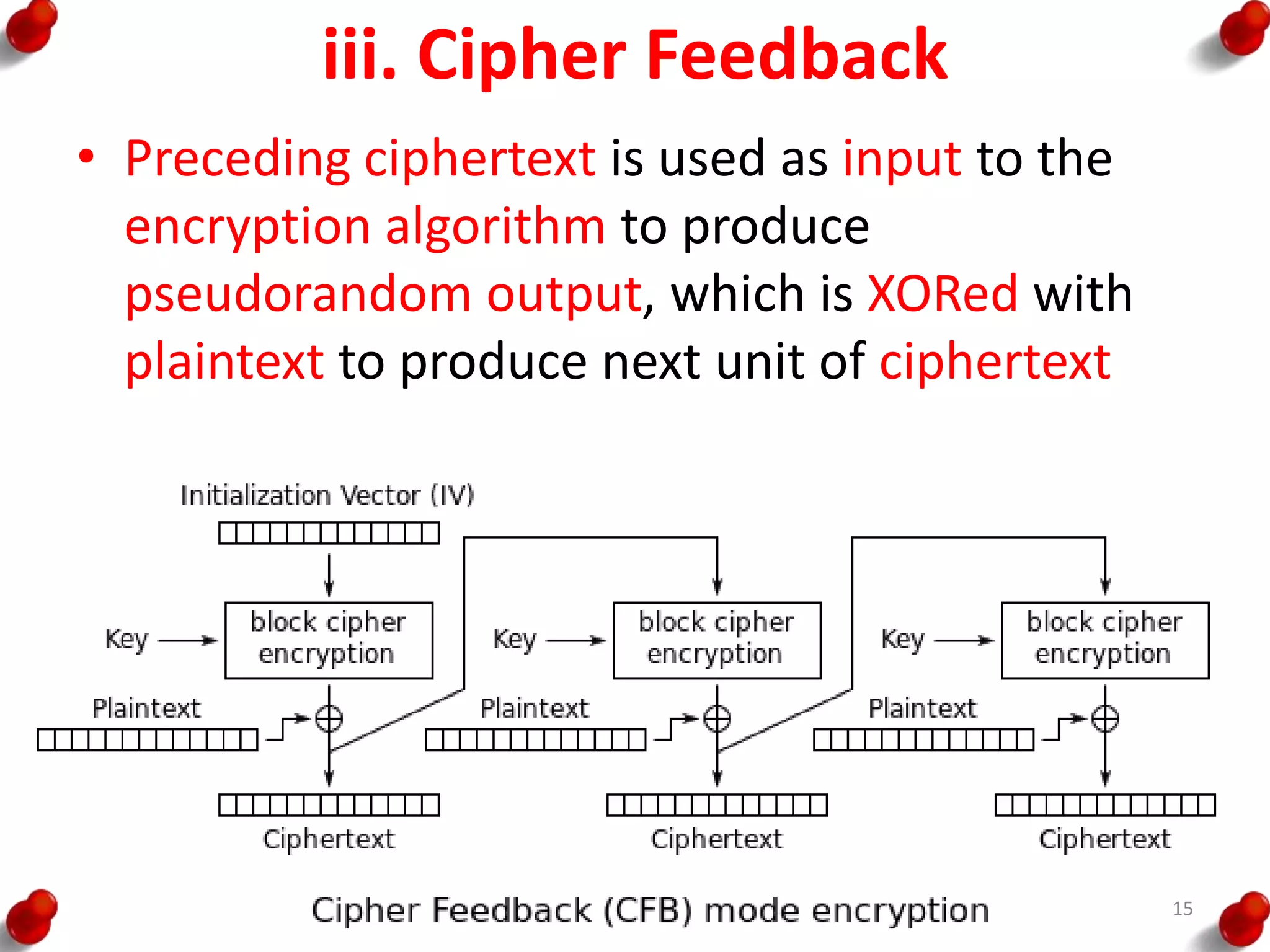
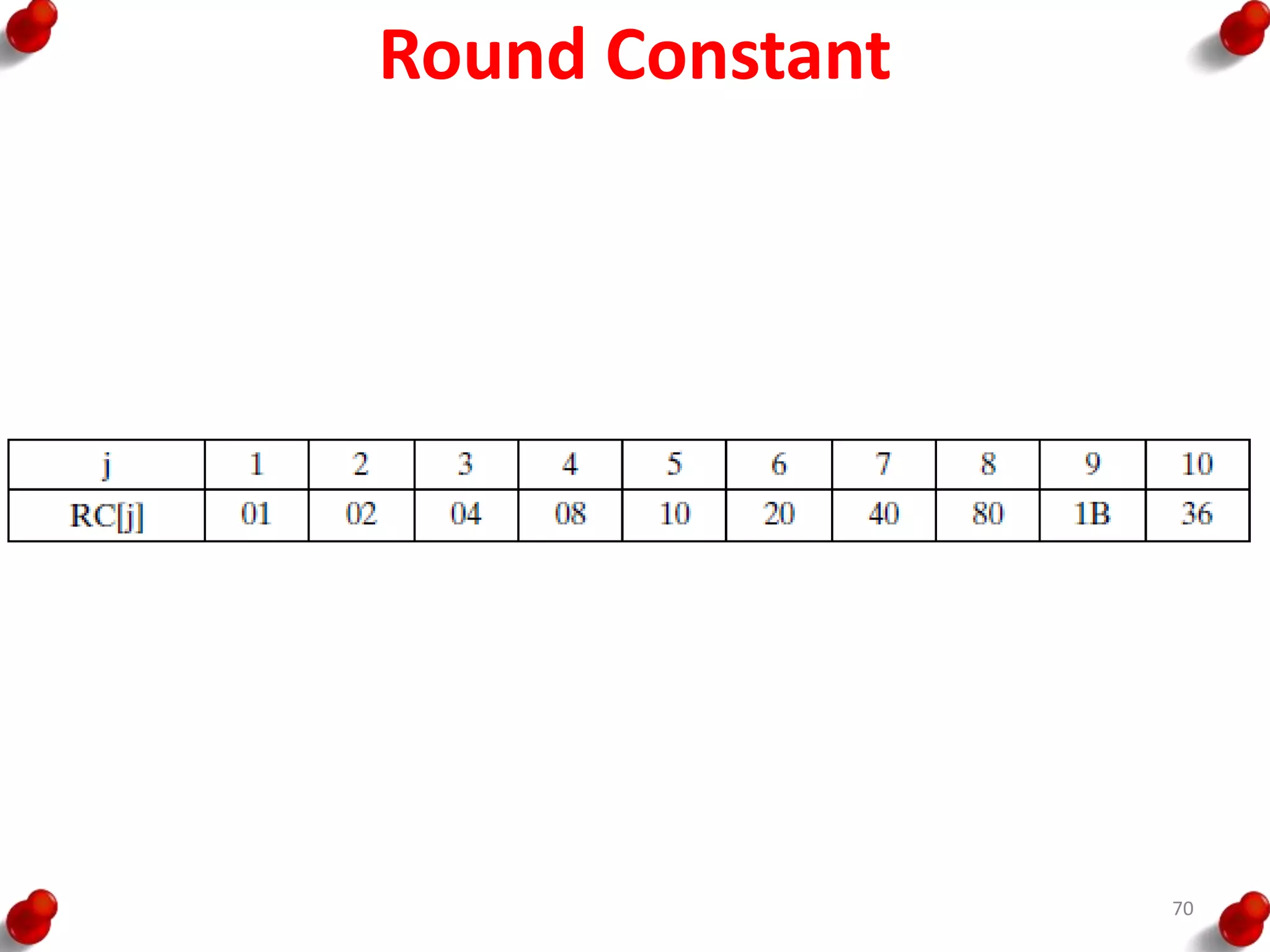
![AES Key Expansion
• RotWord performs a one-
byte circular left shift on a
word. This means that an
input word [B0, B1, B2, B3]
is transformed into [B1, B2,
B3, B0].
• SubWord performs a byte
substitution on each byte of
its input word, using the S-
box.
• The result of steps 1 and 2 is
XORed with a round
constant, Rcon[j].
69](https://image.slidesharecdn.com/blockcipherspublickeycryptography-190918102803/75/Block-ciphers-amp-public-key-cryptography-69-2048.jpg)










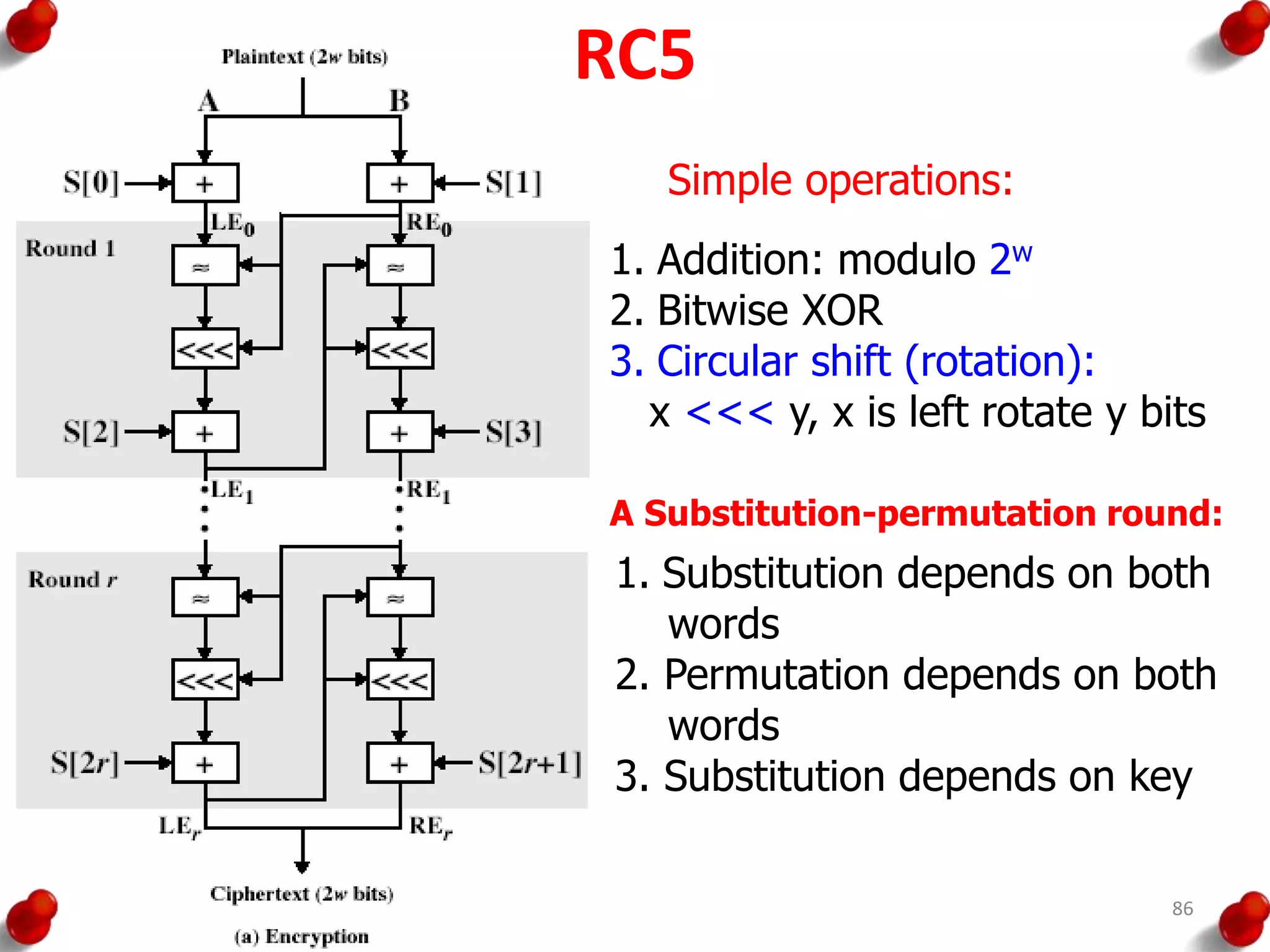
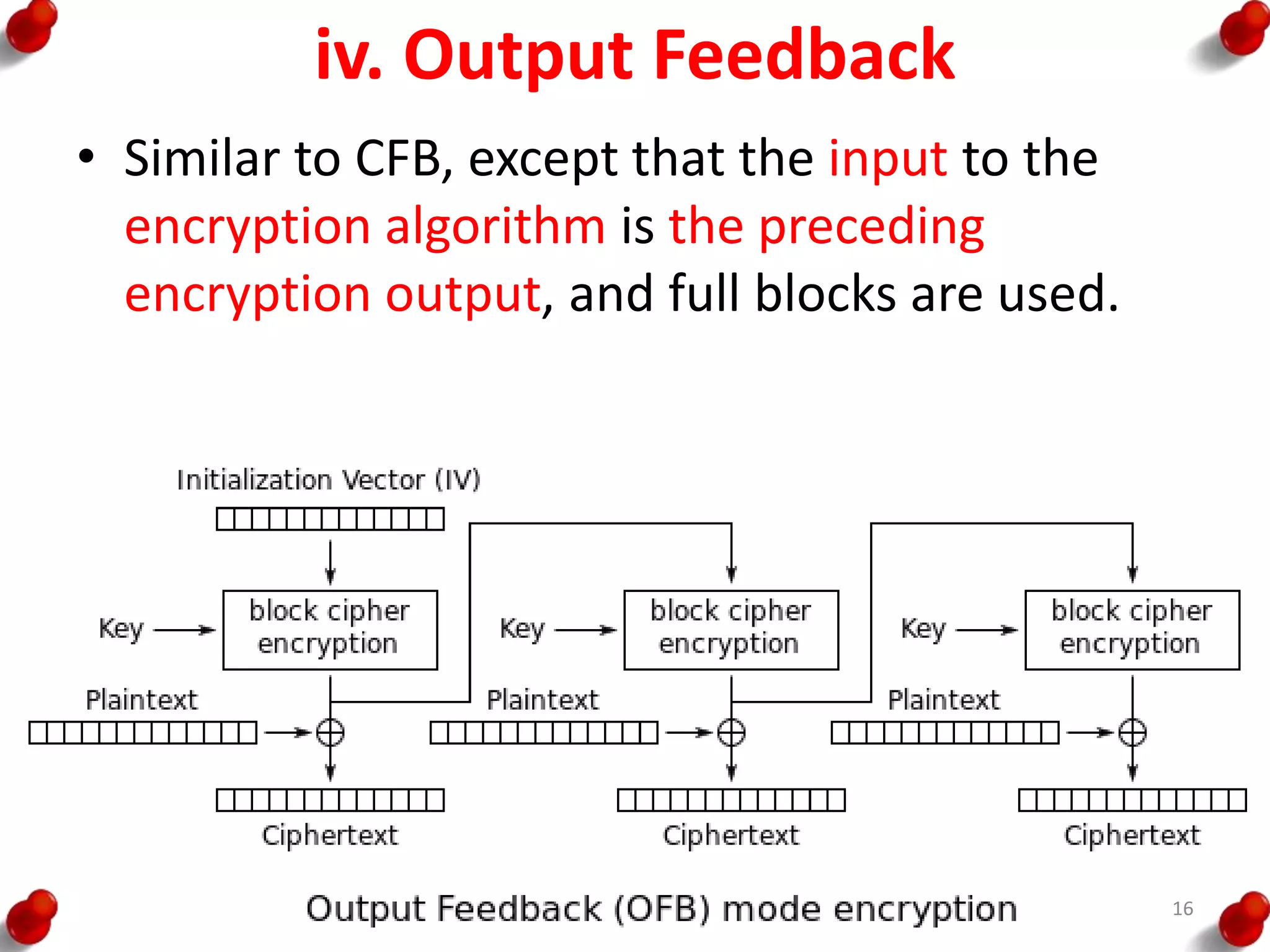
![RC5
• split input into two halves A & B
L0 = A + S[0];
R0 = B + S[1];
for i = 1 to r do
Li = ((Li-1 XOR Ri-1) <<< Ri-1) + S[2 x i];
Ri = ((Ri-1 XOR Li) <<< Li) + S[2 x i + 1];
• each round is like 2 DES rounds
• note rotation is main source of non-linearity
• need reasonable number of rounds (eg 12-16)
87](https://image.slidesharecdn.com/blockcipherspublickeycryptography-190918102803/75/Block-ciphers-amp-public-key-cryptography-87-2048.jpg)


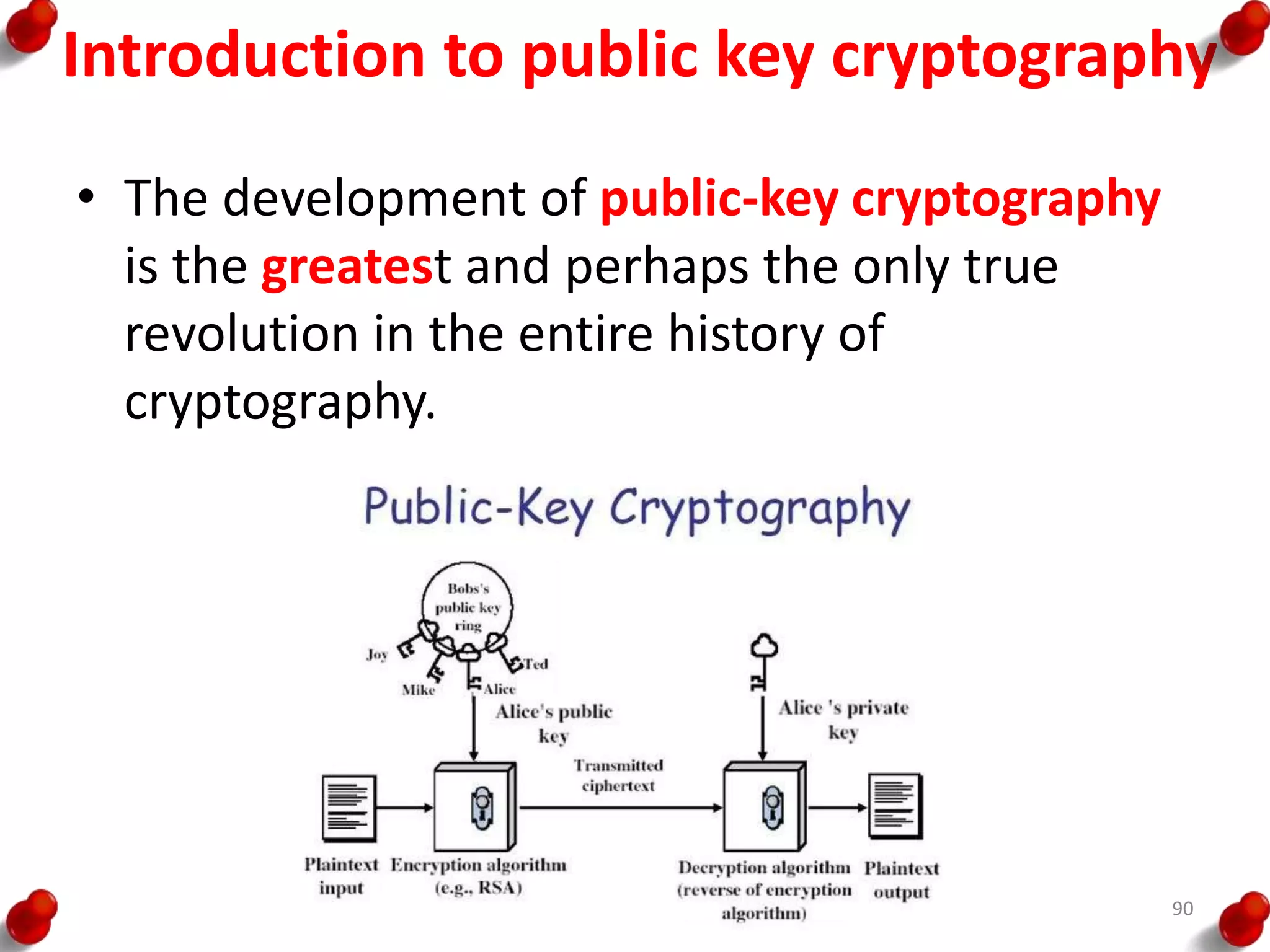


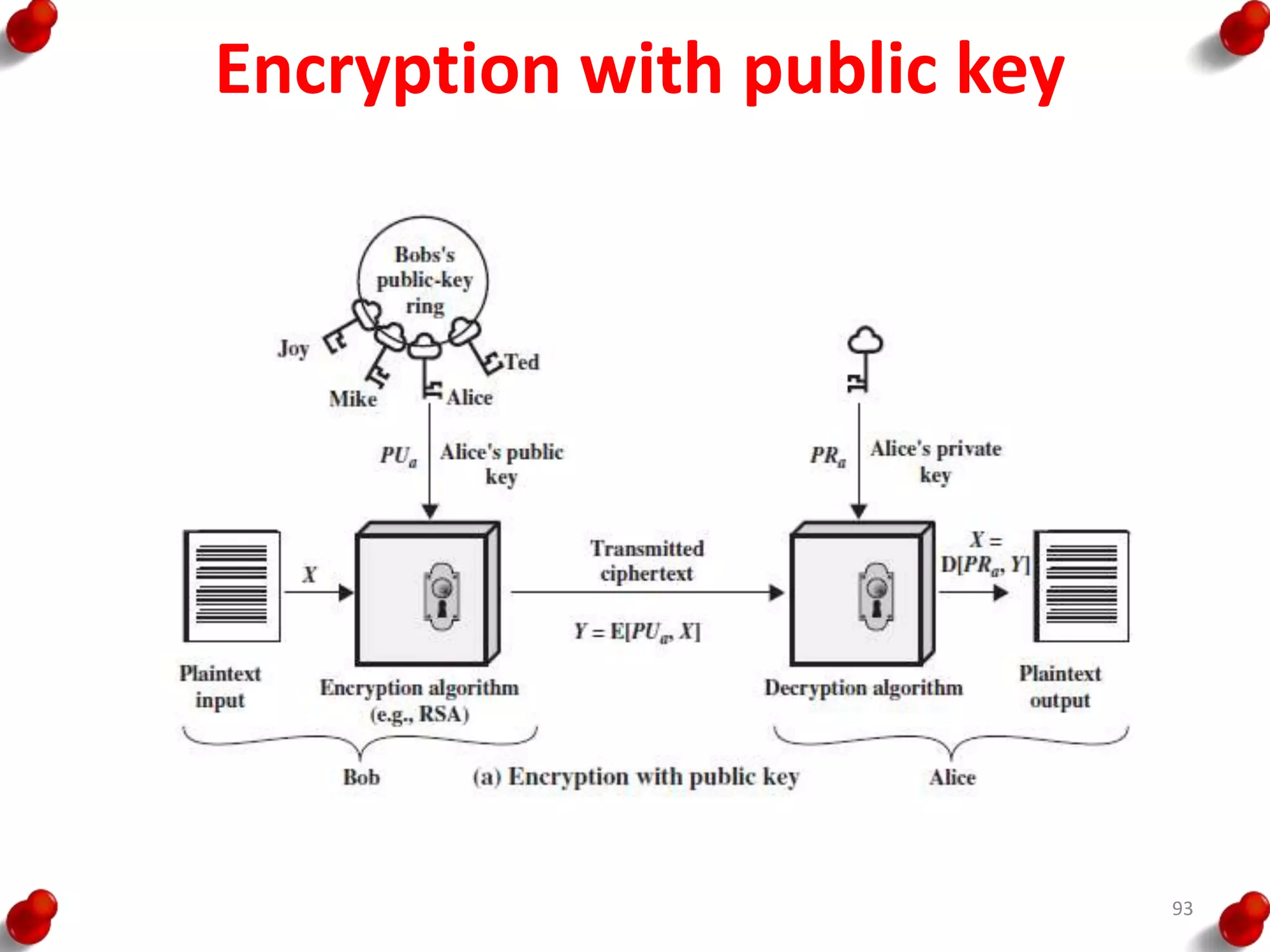
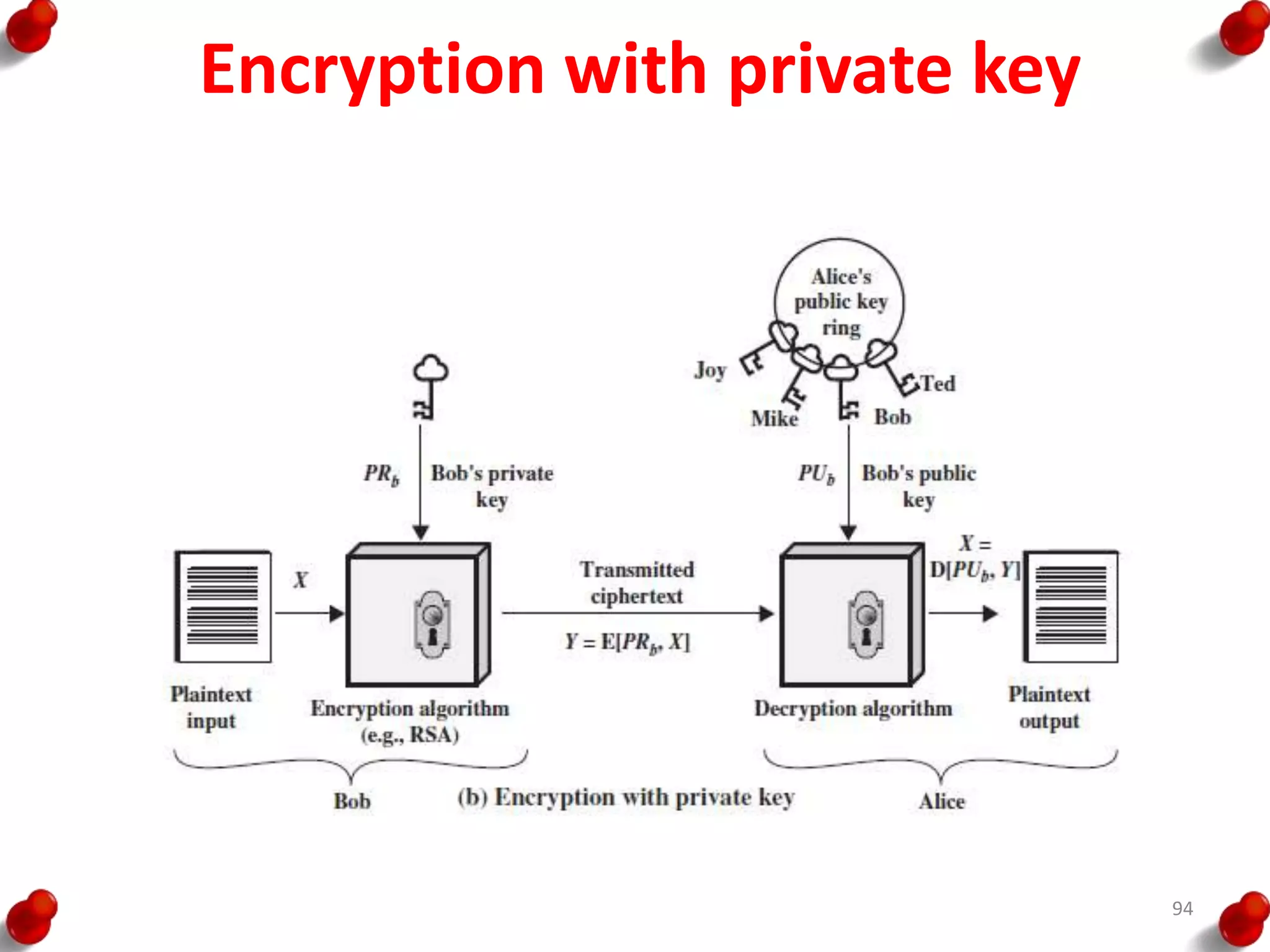





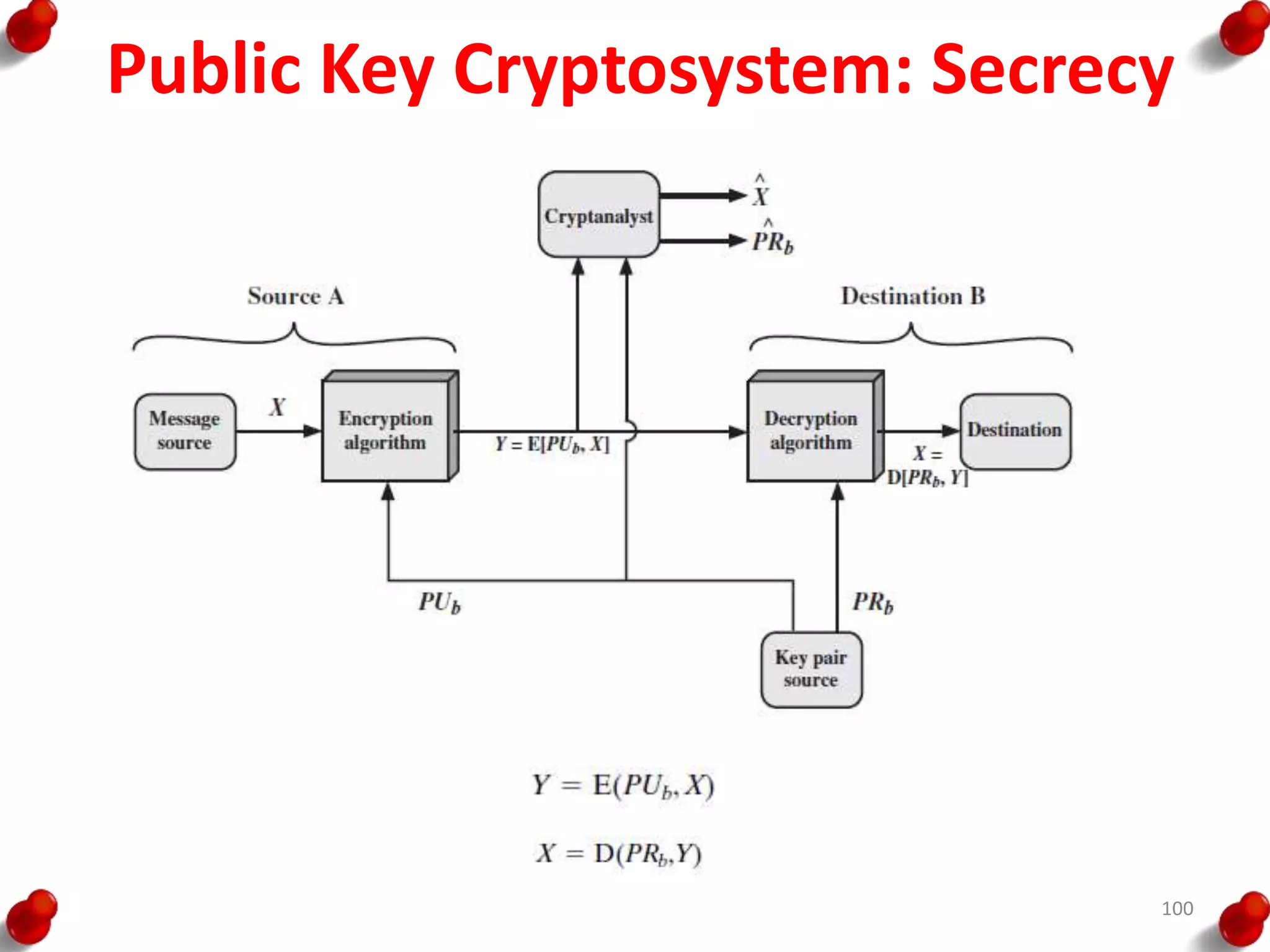
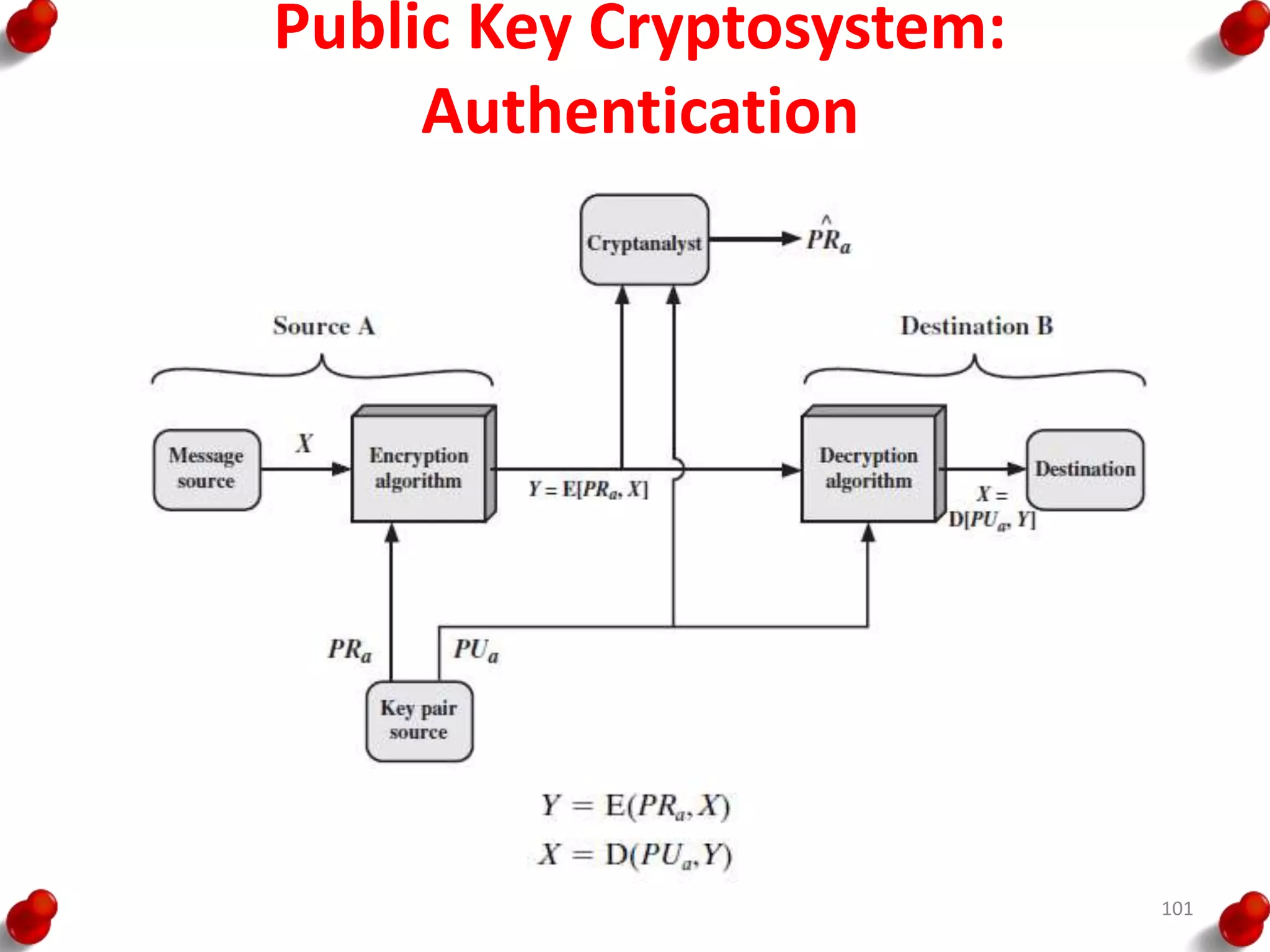
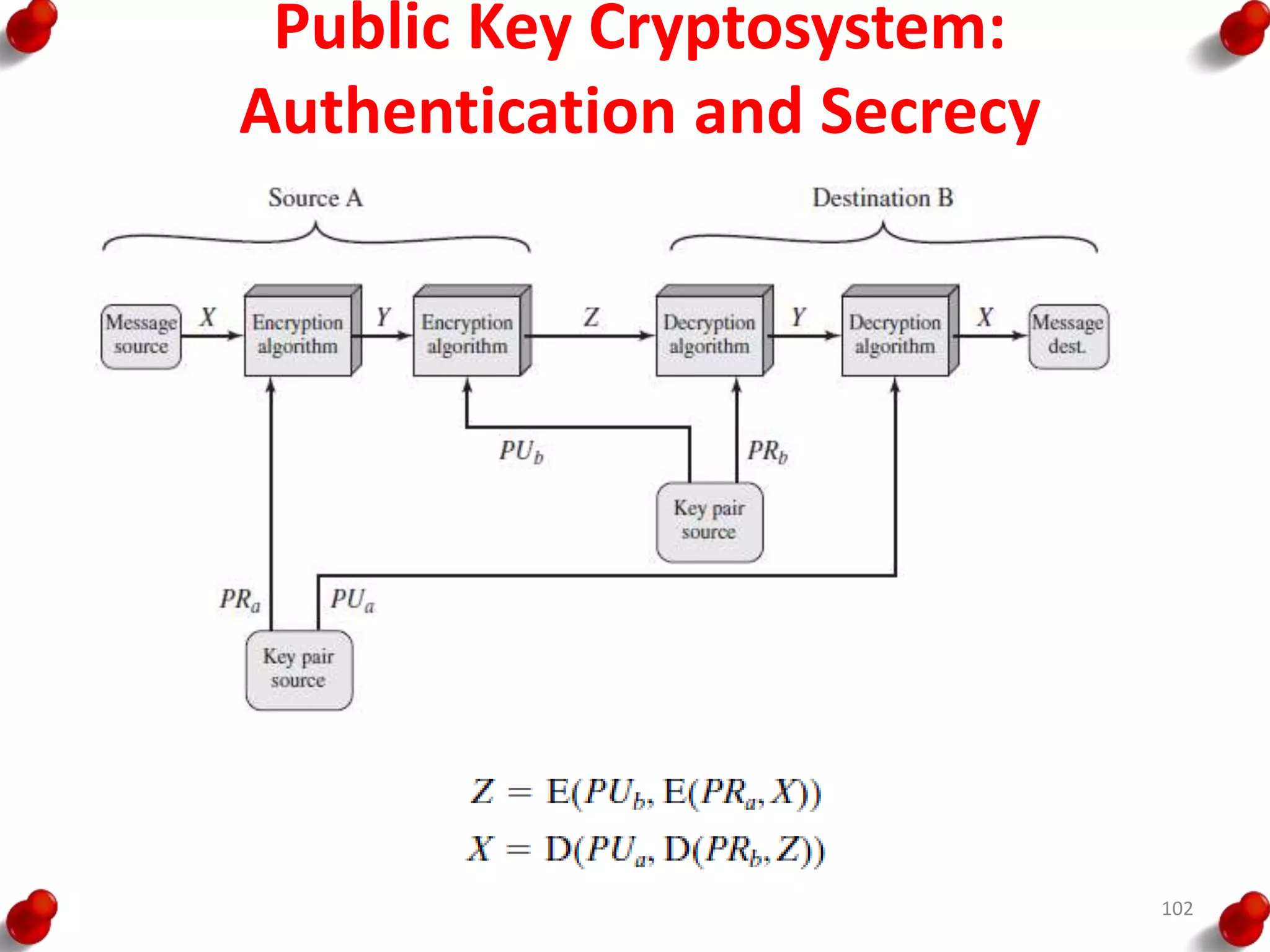

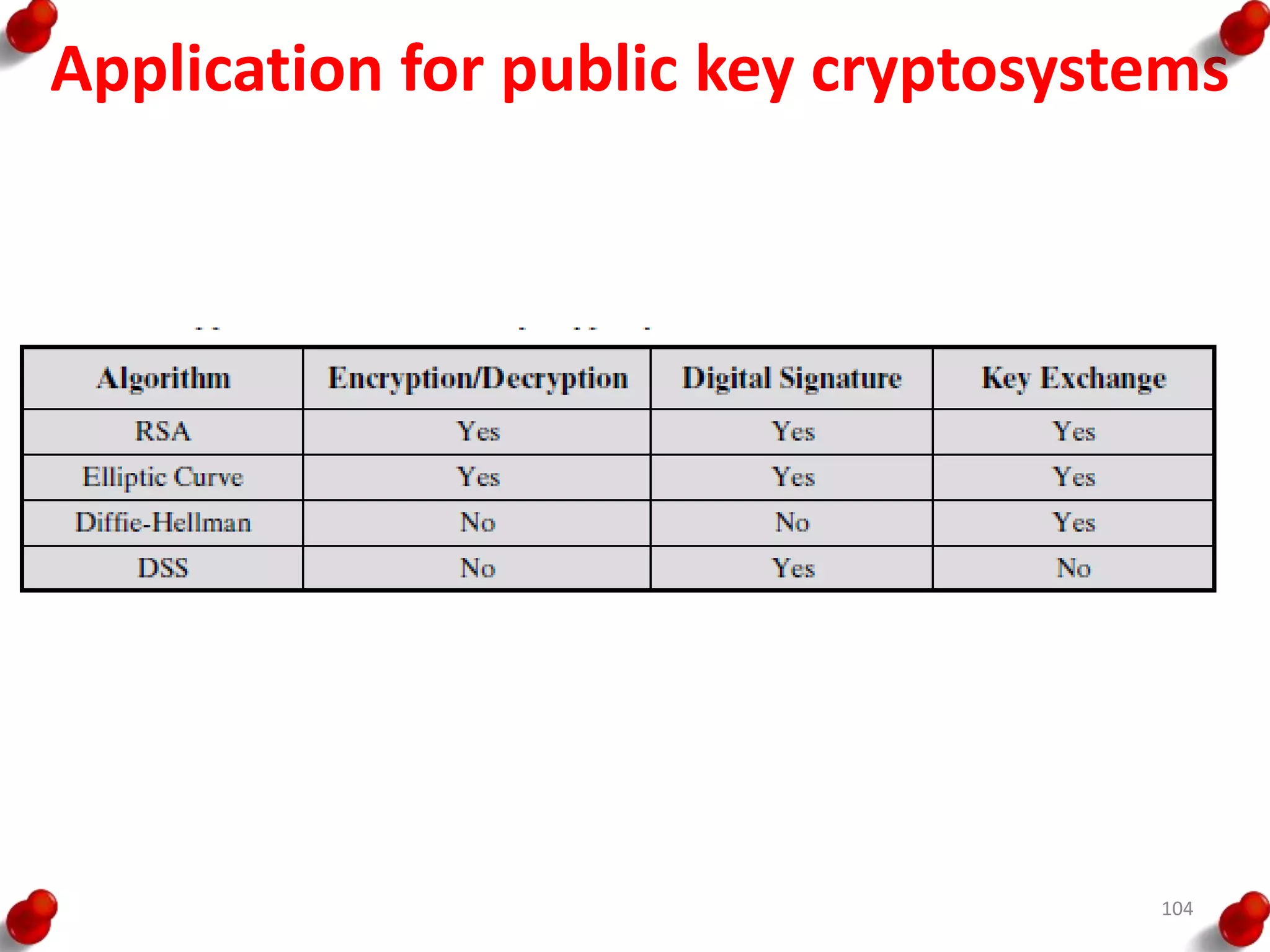








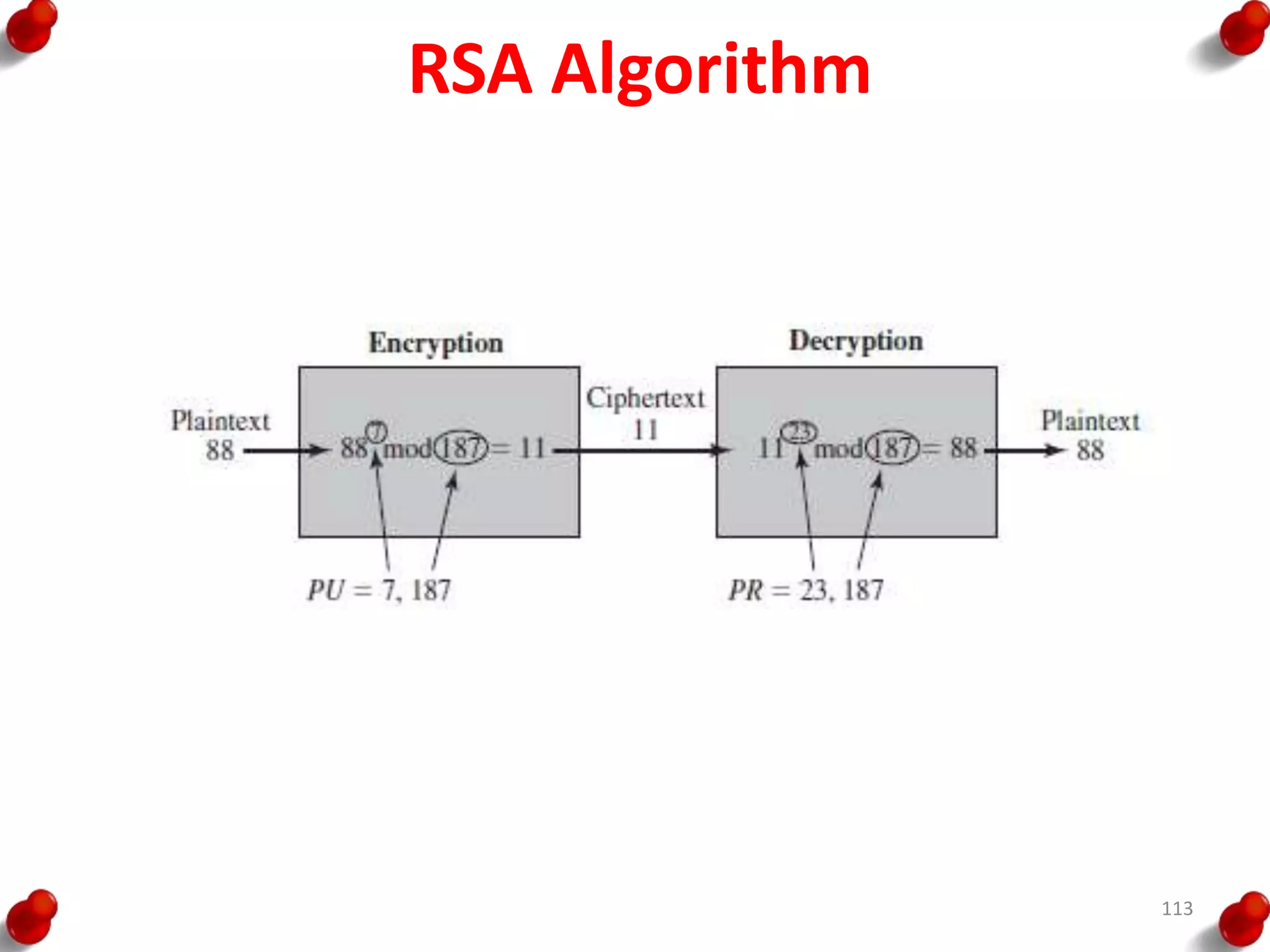
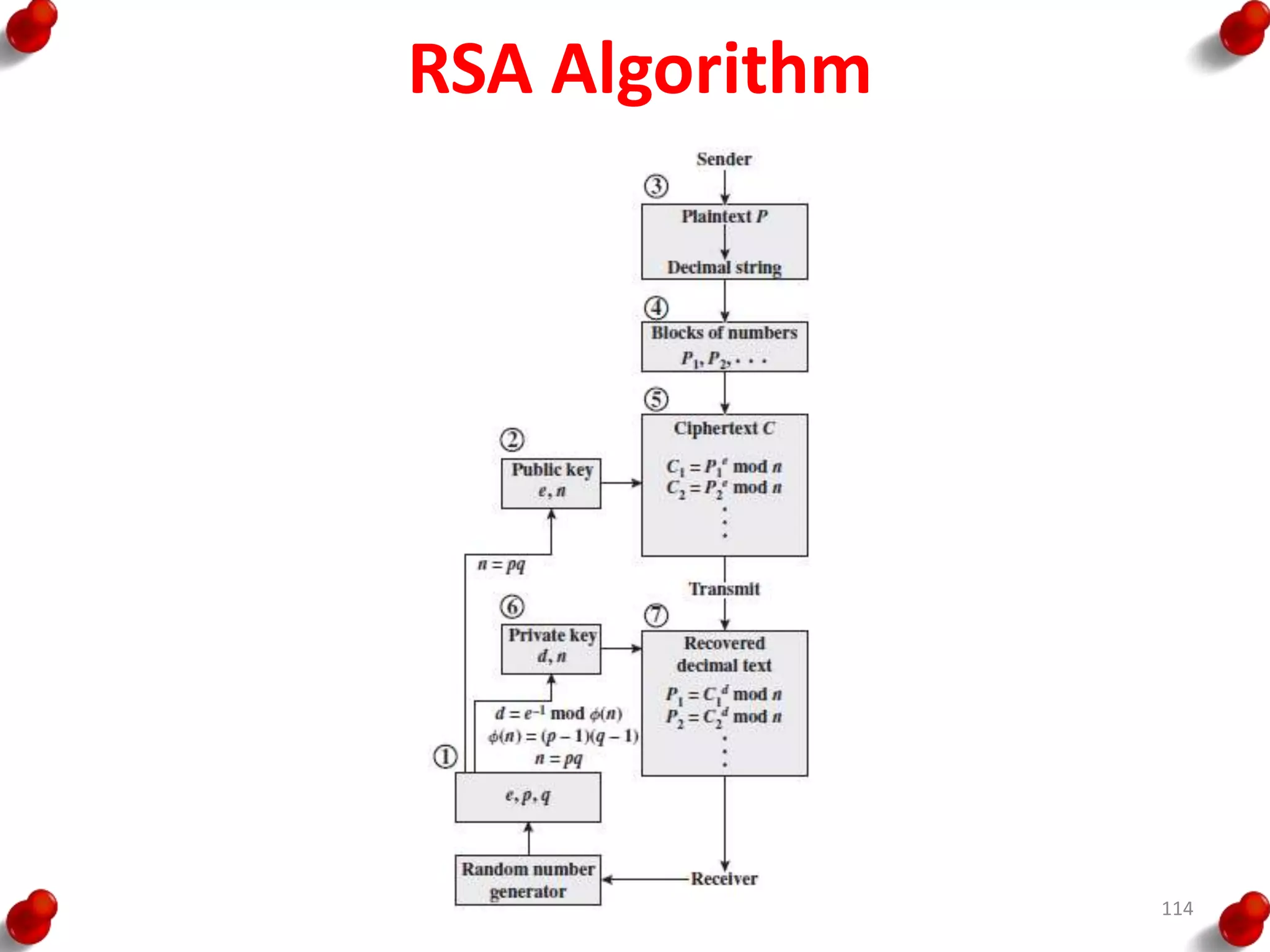
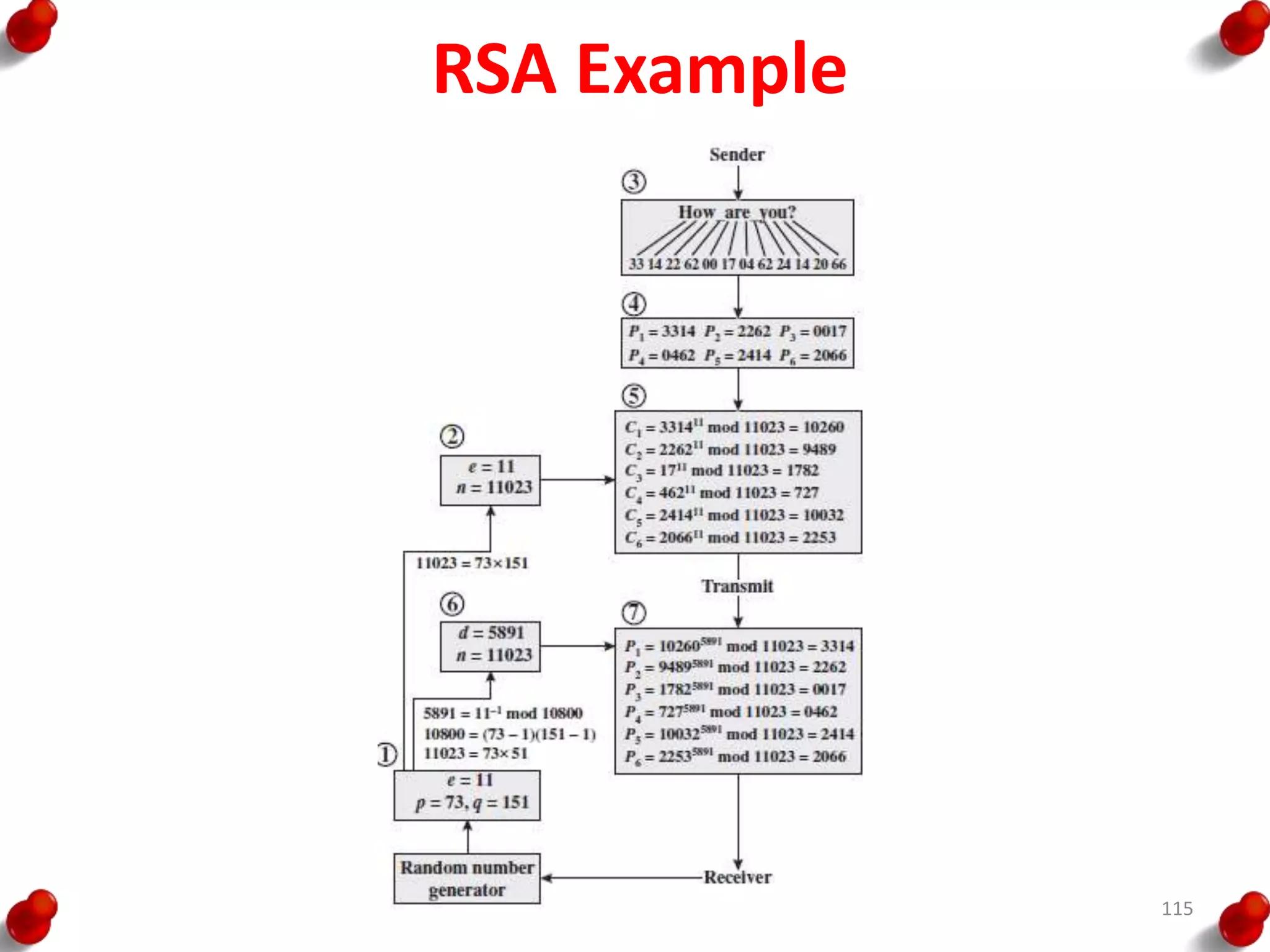



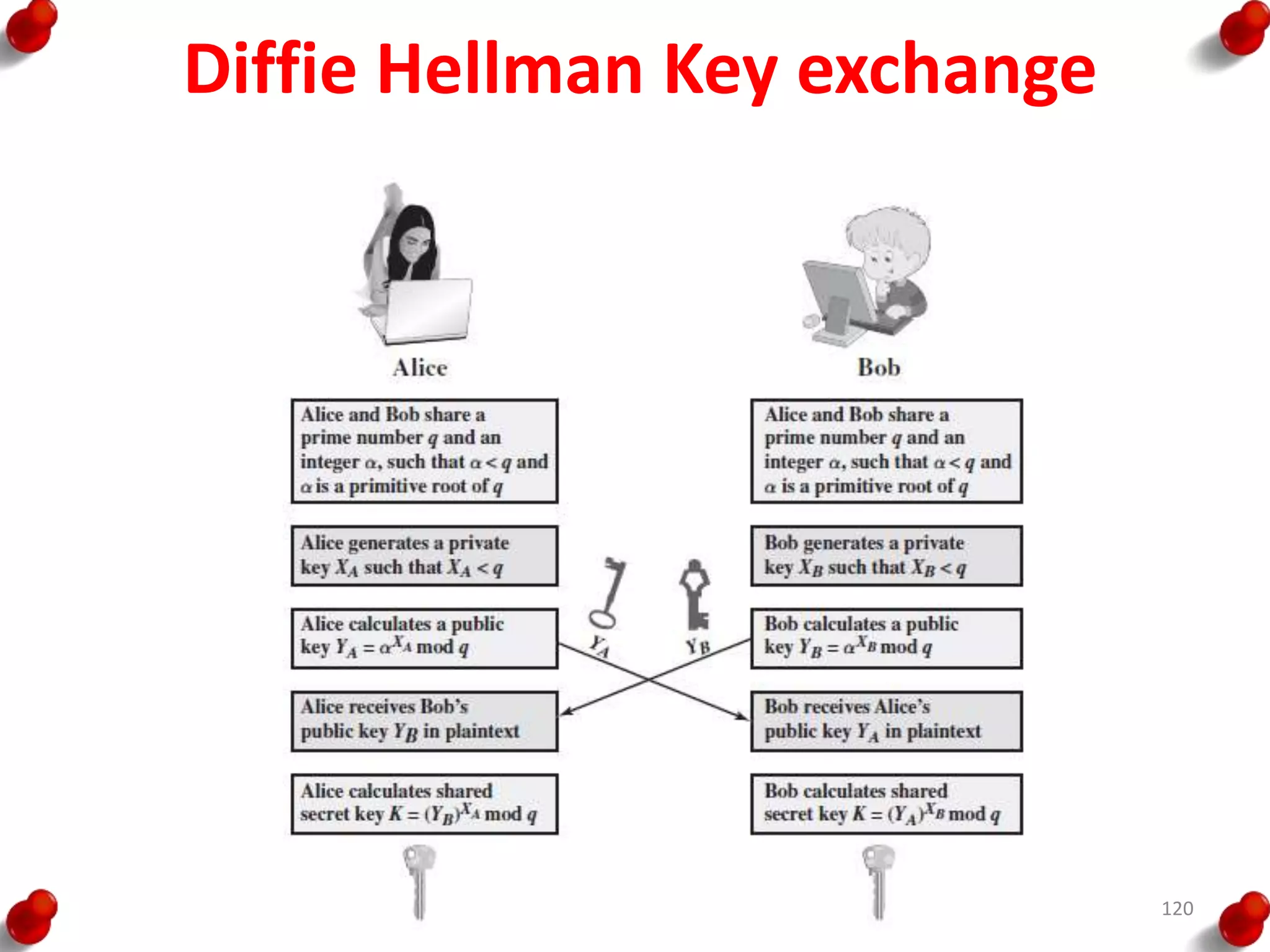
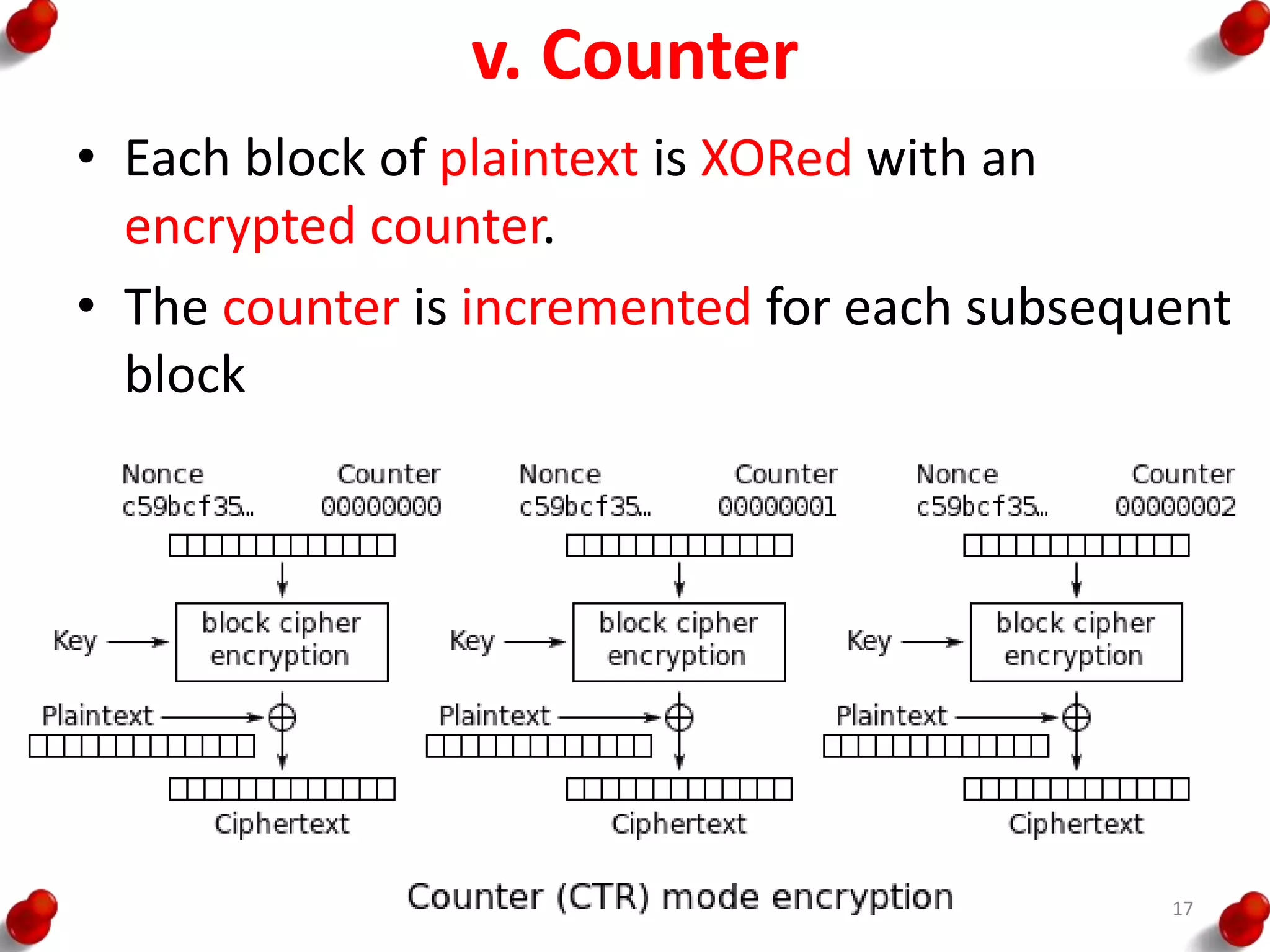
![Diffie Hellman Key exchange
• The first published public-key algorithm
appeared in the seminal paper by Diffie and
Hellman that defined public-key cryptography
[DIFF76b] and is generally referred to as Diffie-
Hellman key exchange
119](https://image.slidesharecdn.com/blockcipherspublickeycryptography-190918102803/75/Block-ciphers-amp-public-key-cryptography-119-2048.jpg)