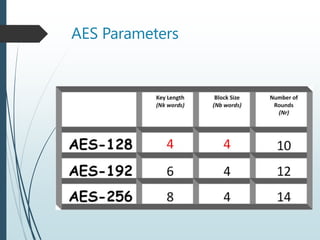
The document describes the Advanced Encryption Standard (AES) algorithm. AES is a symmetric block cipher that encrypts data blocks of 128 bits using a key of 128, 192, or 256 bits. It operates on a 4x4 matrix through a series of transformations including byte substitution, shifting rows, mixing columns, and adding a round key. The algorithm consists of 10, 12, or 14 rounds depending on the key size. AES provides security, efficiency, and flexibility for encryption.

1. ADVANCED ENCRYPTION
STANDARD

2. AES - Algorithm
 Like DES , AES is a symmetric block cipher
 AES is a non feistel cipher that encrypts &decrypts a data
block of 128 bits.
 Block size – 128 bits (PLAIN TEXT)
 Number of rounds – 10 rounds
 Key size-128 bits ( 4 Words/ 16 bytes)
 No of sub keys -44 Sub keys
 Each sub key size = 32 bit/1 Word/4 bytes
 Each round -4 sub keys (128 bits/4 words/16 bytes)
 Pre round calculation – 4 more sub keys (40+4=44 sub
keys) - (128 bits/4 words/16 bytes)
 Cipher text-128 bits

3. AES Parameters

4. Operation of AES
 Based on ‘substitution–permutation network’.
 It comprises of a series of linked operations, some of
which involve replacing inputs by specific outputs
(substitutions) and others involve shuffling bits around
(permutations).
 Computations on bytes rather than bits. Hence, AES
treats the 128 bits of a plaintext block as 16 bytes.
These 16 bytes are arranged in four columns and four
rows for processing as a matrix.
 Unlike DES, the number of rounds in AES is variable and
depends on the length of the key.
 AES uses 10 rounds for 128-bit keys, 12 rounds for 192-
bit keys and 14 rounds for 256-bit keys. Each of these
rounds uses a different 128-bit round key, which is
calculated from the original AES key.

5. BLOCK DIAGRAM - AES

6. Round Process
 In Round 2 [w8….w11] ------ K2
 In Round 3[w12….w16] ------ K3
 …
 In Round 10[w40…w43]------K9
 Total 44 words

7. 10
 Key with variable length (128,192, 256 bit)
• Rappresented with a matrix (array) of bytes with 4 rows
and Nk columns, Nk=key length / 32
• key of 128 bits= 16 bytes  Nk=4
• key of 192 bits= 24 bytes  Nk=6
• key of 256 bits= 32 bytes  Nk=8
Block of length 128 bits=16 bytes
• Represented with a matrix (array) of bytes with 4 rows
and Nb columns, Nb=block length / 32
• Block of 128 bits= 16 bytes  Nb=4
Key and Block
K0,0 K0,1 K0,2 K0,3
K1,0 K1,1 K1,2 K1,3
K2,0 K2,1 K2,2 K2,3
K3,0 K3,1 K3,2 K3,3
in0 in4 in8 in12
in1 in5 in9 in13
in2 in6 in10 in14
in3 in7 in11 in15
in=input

8. • Internally, the AES algorithm’s operations are performed on a
two-dimensional array of bytes called the State
– 4 rows, each containing Nb bytes
– Nb columns, costituted by 32-bit words
– Sr,c denotes the byte in row r and column c
 The array of bytes in input is copied in the State matrix
State arrays
8
 At the end, the State matrix is copied in the output matrix
Sr,c  in
Sr,c  in
out Sr,c
out Sr,c
S0,0 S0,1 S0,2 S0,3
S1,0 S1,1 S1,2 S1,3
S2,0 S2,1 S2,2 S2,3
S3,0 S3,1 S3,2 S3,3

9. Output array
Out0 Out4 Out8 Out12
Out1 Out5 Out9 Out13
Out2 Out6 Out10 Out14
Out3 Out7 Out11 Out15
S0,0 S0,1 S0,2 S0,3
S1,0 S1,1 S1,2 S1,3
S2,0 S2,1 S2,2 S2,3
S3,0 S3,1 S3,2 S3,3

10. KEY –Expansion (128 bits)
W0 W1 W2 -------- W43

11. Substitution Types (S-BOX)
 INPUT OF THE S-BOX – 8 bits
 First four bits – Row number (0 to 15)
 Next four bits – Column number(0 to 15)
 Size (16x16)
 Eg : 0000 0101
 0th –row
 5th column
 Result -52 ( again converted into 8 bits)

12. Byte Substitution
• a simple substitution of each byte
• uses one table of 16x16 bytes containing a
permutation of all 256 8-bit values
• each byte of state is replaced by byte in row (left
4-bits) & column (right 4-bits)
– eg. byte {95} is replaced by row 9 col 5 byte
– which is the value {2A}
• S-box is constructed using a defined
transformation of the values in GF(28)
• designed to be resistant to all known attacks

13. 15
SubBytes Transformation
• S’r,c  S-box(Sr,c)
• S’r,c  S-box(Sr,c)
S0,0 S0,1 S0,2 S0,3
S1,0
S2,0
,1
S S2,3
S3,0 S3,1 S3,2 S3,3
S’0,0 S’0,1 S’0,2 S’0,3
S’1,0 ’1,1 S’1,2 S’1,3
S’2,0 S’2,1 S’2,2 S’2,3
S’3,0 S’3,1 S’3,2 S’3,3
S1 S1,2 S1,3
S
S2,1
r,c
2,2
S
S’r,c
S-box
Bytes are transformed using a non-linear S-box

14. 0 1 2 3 4 5 6 7 8 9 A B C D E F
0 63 7C 77 7B F2 6B 6F C5 30 01 67 2B FE D7 AB 76
1 CA 82 C9 7D FA 59 47 F0 AD D4 A2 AF 9C A4 72 C0
2 B7 FD 93 26 36 3F F7 CC 34 A5 E5 F1 71 D8 31 15
3 04 C7 23 C3 18 96 05 9A 07 12 80 E2 EB 27 B2 75
4 09 83 2C 1A 1B 6E 5A A0 52 3B D6 B3 29 E3 2F 84
5 53 D1 00 ED 20 FC B1 5B 6A CB BE 39 4A 4C 58 CF
6 D0 EF AA FB 43 4D 33 85 45 F9 02 7F 50 3C 9F A8
7 51 A3 40 8F 92 9D 38 F5 BC B6 DA 21 10 FF F3 D2
8 CD 0C 3 EC 5F 97 44 17 C4 A7 7E 3D 64 5D 19 73
9 60 81 4F DC 22 2A 90 88 46 EE B8 14 DE 5E 0B DB
A E0 32 3A 0A 49 06 24 5C C2 D3 AC 62 91 95 E4 79
B E7 C8 37 6D 8D D5 4E A9 6C 56 F4 EA 65 7A AE 08
C BA 78 25 2E 1C A6 B4 C6 E8 DD 74 1F 4B BD 8B 8A
D 70 3E B5 66 48 03 F6 0E 61 35 57 B9 86 C1 1D 9E
E E1 F8 98 11 69 D9 8E 94 9B 1E 87 E9 CE 55 28 DF
F 8C A1 89 0D BF E6 42 68 41 99 2D 0F B0 54 BB 16
S-box Table
17
Example: hexa 53 is replaced with hexa ED
(The first 4 bits in the byte(the first hexadecimal value, hence) individuate the row,
the last 4 bits individuate the column)

15. SHIFT ROWS
 In the Shift Rows phase of AES, each row of the 128-bit
internal state of the cipher is shifted.
 The rows in this stage refer to the standard
representation of the internal state in AES, which is a
4x4 matrix where each cell contains a byte.
 Bytes of the internal state are placed in the matrix
across rows from left to right and down columns.
 In the Shift Rows operation, each of these rows is
shifted to the left by a set amount: their row number
starting with zero.
 The top row is not shifted at all, the next row is shifted
by one and so on.

16. ShiftRows
1
6
• Circular Left Shift of a number of bytes equal
to the row number
S0,0 S0,1 S0,2 S0,3
S1,0 S1,1 S1,2 S1,3
S2,0 S2,1 S2,2 S2,3
S3,0 S3,1 S3,2 S3,3
S0,0 S0,1 S0,2 S0,3
S1,1 S1,2 S1,3 S1,0
S2,2 S2,3 S2,0 S2,1
S3,3 S3,0 S3,1 S3,2

17. SHIFT ROWS

18. MIX COLUMNS
 Unlike standard matrix multiplication, Mix Columns
performs matrix multiplication as per Galois Field 28.
 It is important to note that this multiplication has the
property of operating independently over each of the
columns of the initial matrix, i.e. the first column when
multiplied by the matrix, produces the first column of
the resultant matrix.

19. MIX COLUMNS

20. MixColumns Transformation
S0,1 S0,2 S0,3
S S1,
1
1,2
S S1,3
S2,2 S2,3
S
S2,
S3, 3,2
S S3,3
S’0,1 S’0,
2
S’0,
3
S’1,1 S’1,2 S’1,3
S’2,1 S’2,
2
S’2,
3
S’2,
0
S’3,
0
S’3, S’3,
2
S’3,
3
1,0
S1,c
S2,0
S 1
2,c
3,0 1
S3,c
S0,0
S0,c
S’2,c
S’3,c
1
S’0,
S’
0 0,c
S’1,0 S’1,c
MixColumns()



 
 

 









1,c 
'
3,c
2,c

'
1,c
0,c

02 S3,c
03 S2,c 
01 S
01 S0,c
02 03 01
01 02 03
01 01 02
03 01 01
S
S'
S
S'
Bytes in columns are combined linearly
Multiply mod x4+1 with a(x)
a(x) = {03}x3 + {01}x2 + {01}x +{02}

21. Mix Columns
• each column is processed separately
• each byte is replaced by a value
dependent on all 4 bytes in the column
• effectively a matrix multiplication in GF(28)
using prime poly m(x) =x8+x4+x3+x+1

22. Add Round Key
• XOR state with 128-bits of the round key
• again processed by column (though
effectively a series of byte operations)
• inverse for decryption is identical since
XOR is own inverse, just with correct
round key
• designed to be as simple as possible

23. Add Round Key
• State is represented as follows (16 bytes):
• AddRoundKey(State, Key):
S0,0 S0,1 S0,2 S0,3
S1,0 S1,1 S1,2 S1,3
S2,0 S2,1 S2,2 S2,3
S3,0 S3,1 S3,2 S3,3
Key State State 14

24. AES EvaluationCriteria
• initial criteria:
– security – effort to practically cryptanalyse
– cost – computational
– algorithm & implementation characteristics
• final criteria
– general security
– software & hardware implementation ease
– implementation attacks
– flexibility (in en/decrypt, keying, other factors)

25. AES Round

26. AES Key Expansion
• takes 128-bit (16-byte) key and expands
into array of 44/52/60 32-bit words
• start by copying key into first 4 words
• then loop creating words that depend on
values in previous & 4 places back
– in 3 of 4 cases just XOR these together
– every 4thhas S-box + rotate + XOR constant of
previous before XOR together
• designed to resist known attacks

27. AES Decryption
• AES decryption is not identical to
encryption since steps done in reverse
• but can define an equivalent inverse
cipher with steps as for encryption
– but using inverses of each step
– with a different key schedule
• works since result is unchanged when
– swap byte substitution & shift rows
– swap mix columns & add (tweaked) round key