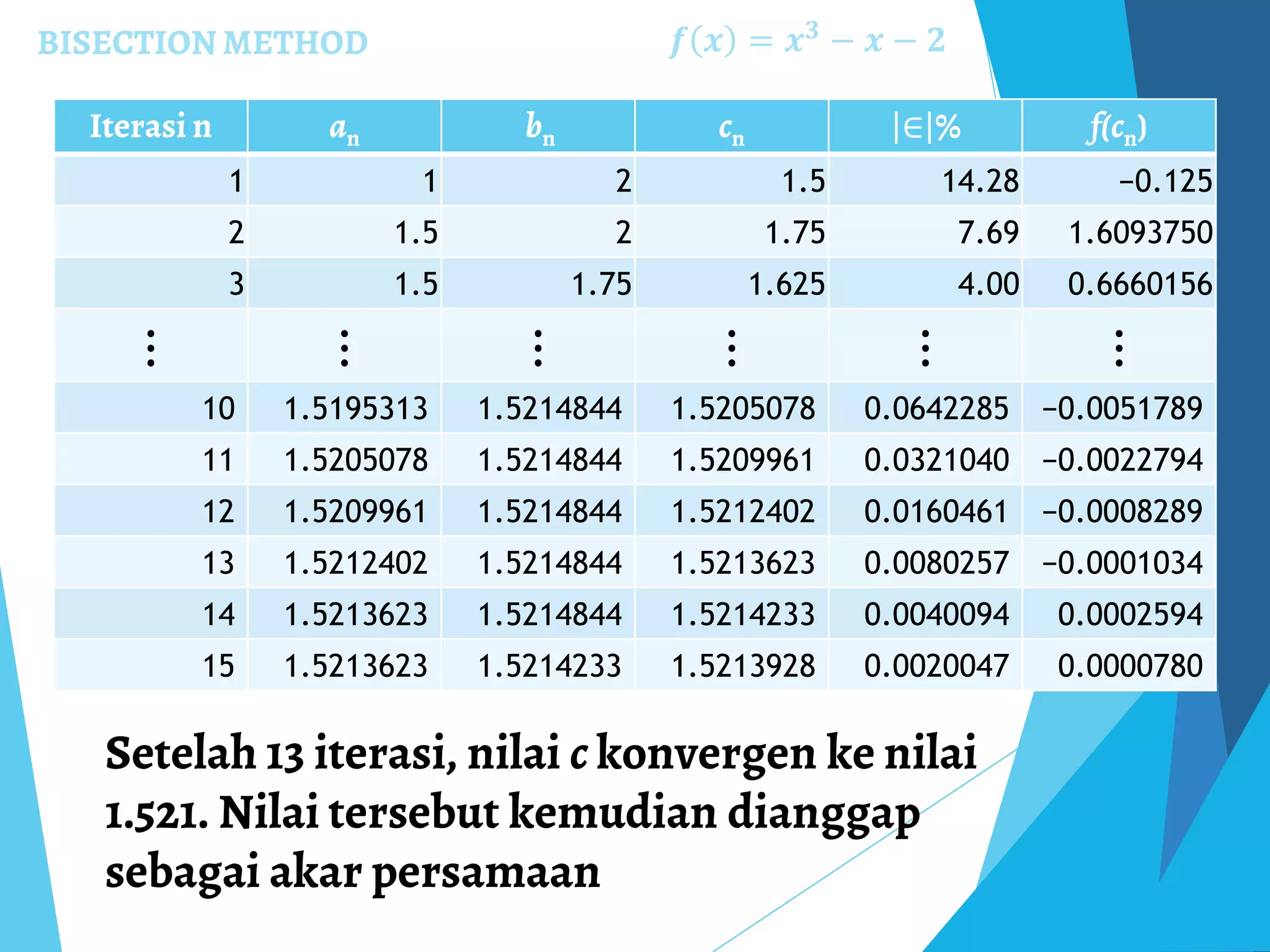
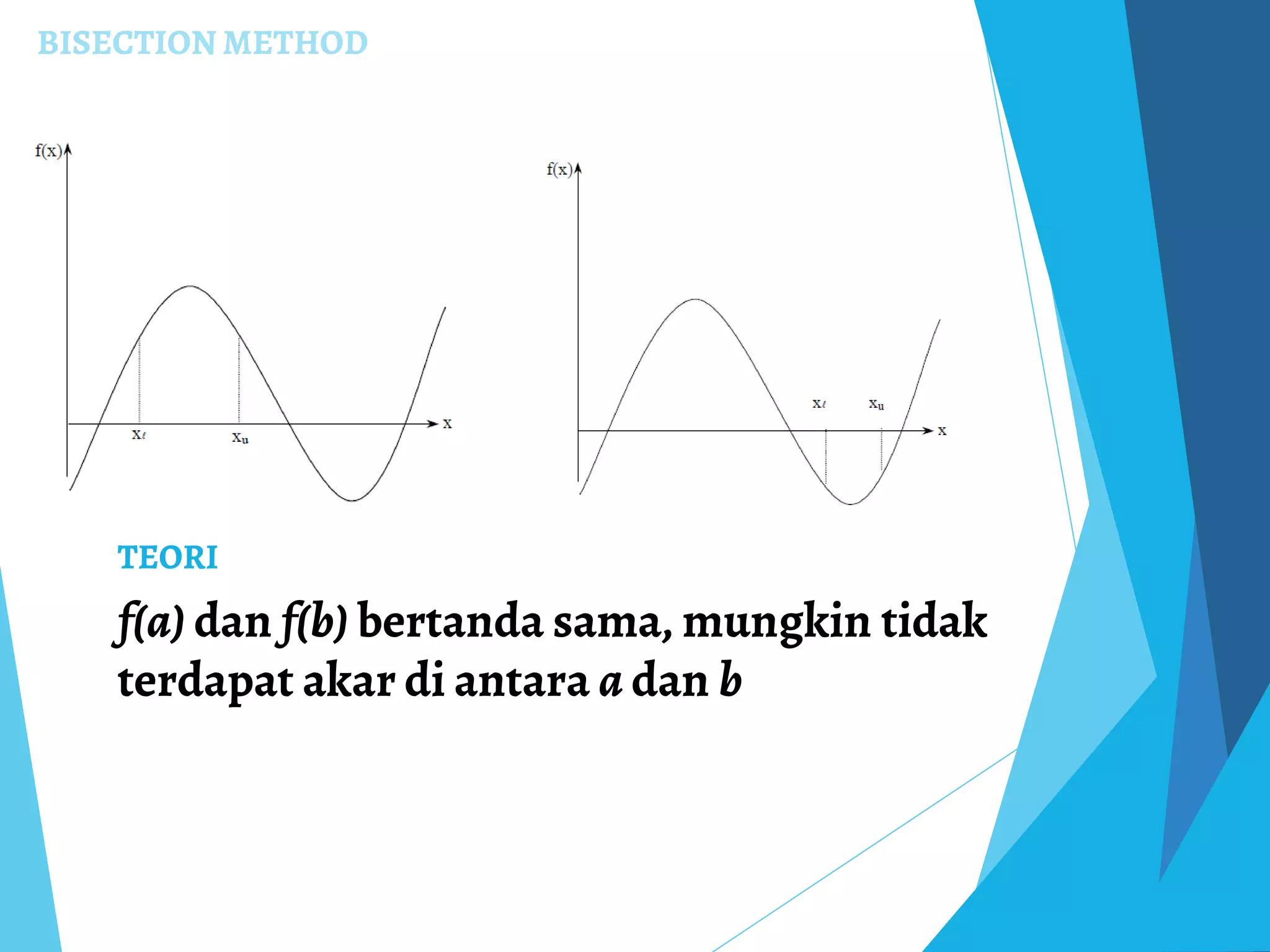
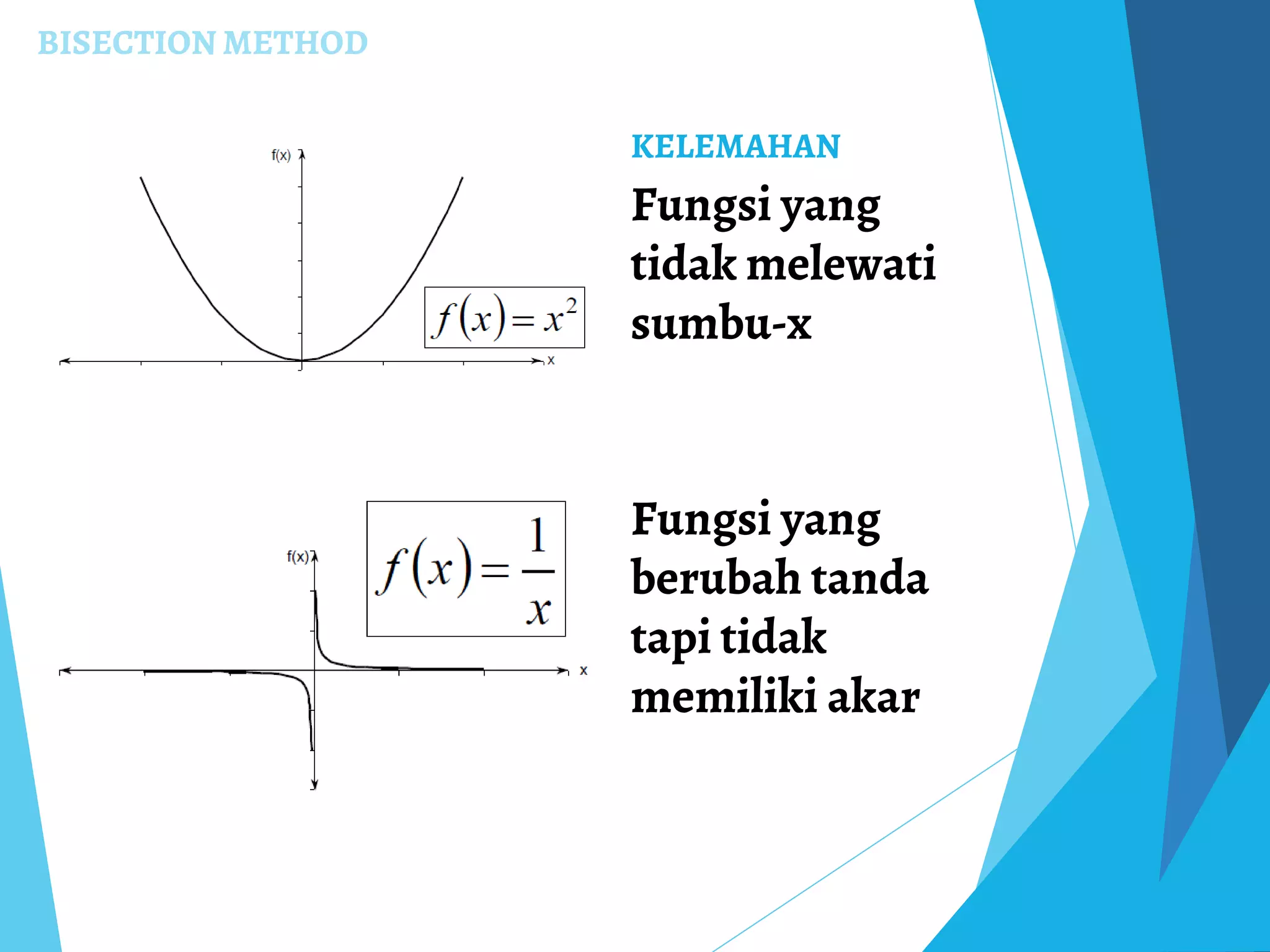
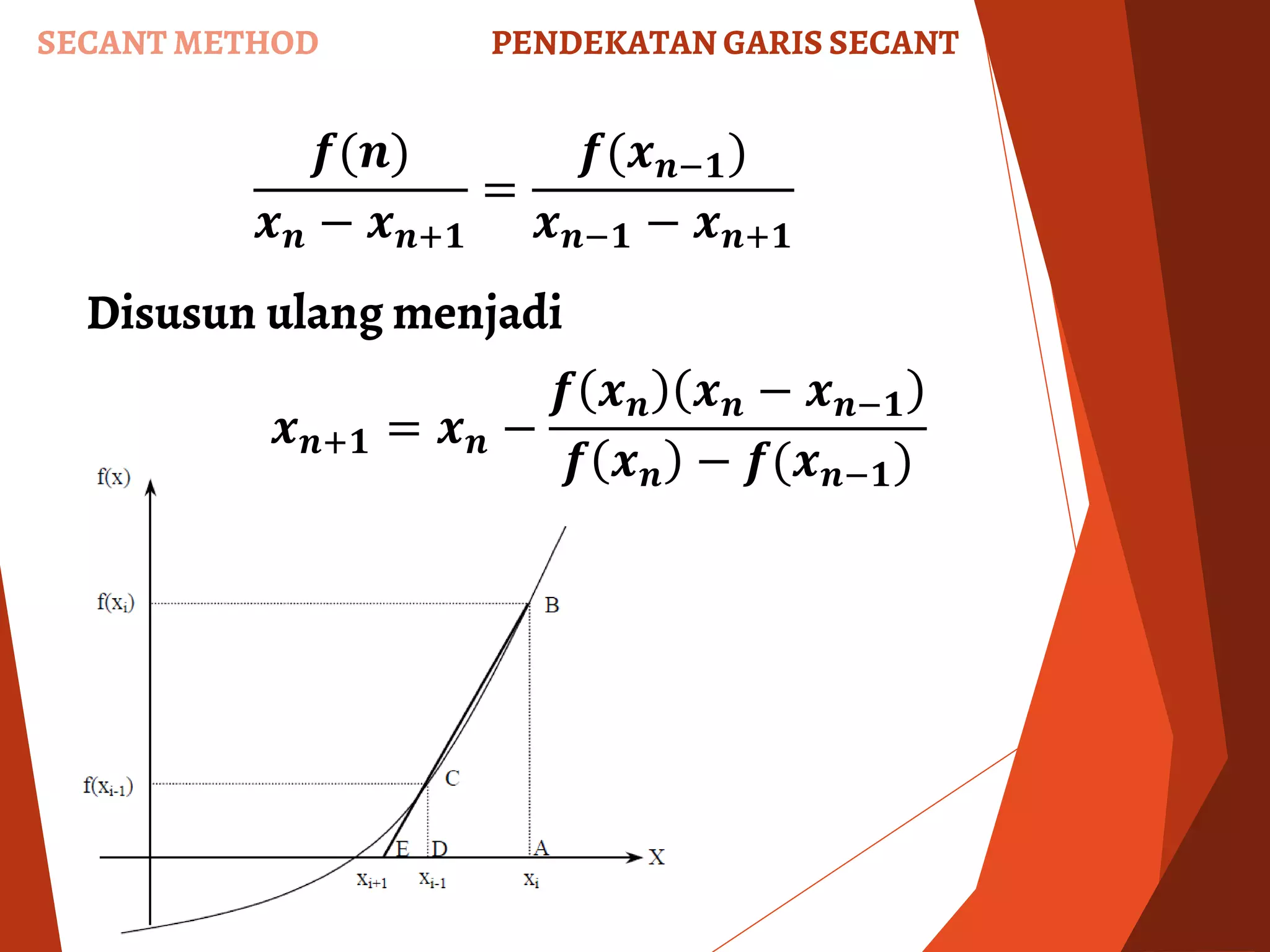
Dokumen ini membahas tentang metode numerik untuk mencari akar persamaan non-linear, termasuk metode bisection, Newton-Raphson, dan secant. Setiap metode dijelaskan dengan langkah-langkah, kelebihan, dan kelemahannya, serta analisis konvergensi. Selain itu, dokumen ini juga mencakup penugasan kelompok yang meminta implementasi metode-metode tersebut dalam bahasa pemrograman yang berbeda dari MATLAB.