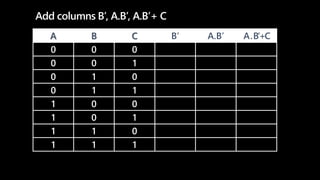
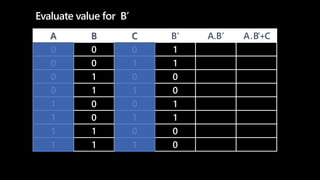
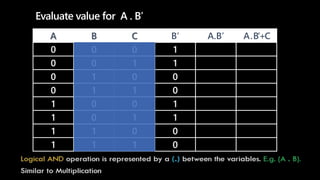
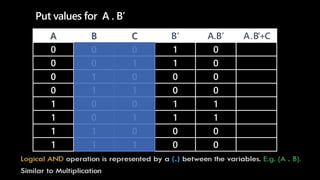
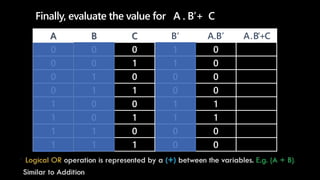
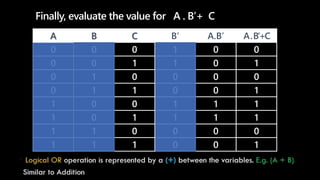
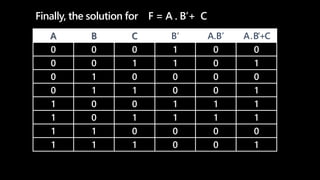
A truth table represents all possible combinations of values for logical variables and statements and the resulting outputs. It has 2^n rows where n is the number of variables. Each row lists the values for the variables and the output of the logical expression. To evaluate an expression, populate the truth table by filling in the variable values in each row then evaluate the expression for each row according to the precedence of operators - NOT, then AND, then OR. Parentheses are evaluated first. An example shows constructing a truth table to evaluate the expression F=A.B'+C.

1. Introduction and Basic Concepts

5. TRUTH TABLE
Truth Table is a table which represents all the possible values of
logical variables/ statements along with all the possible results of the
given combinations of values.
With the help of truth table we can know all the possible
combinations of values and results of logical statements.

6. Logic variables are combined by the means of logical
operators (AND, OR, NOT) to form a Boolean expression.
For example X + YZ + XY is a Boolean expression.
It is often convenient to write X.Y.Z as XYZ
In order to study a Boolean expression, it is useful to
construct a table of values for the variables and then
evaluate the expression for each possible combination of
values.
Evaluating Boolean expression

7. NOTE : A truth table of n input variables will have 2n input
combinations i.e. 2n rows, for e.g. a 4-variable truth table
will have 2n i.e. 16 rows in it.
So if we have a 2 input variables say X and Y we have n=2,
hence we have 22 =4 rows as following-
X Y
0 0
0 1
1 0
1 1

8. In case we have a 3 input variables say X , Y and Z, we
have n=3, hence we have 23 =8 rows as following-
X Y Z
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

12. SOLVING SIMPLE QUESTIONS
While evaluating Boolean expression there is a
precedence order which has to be taken care of always. The
order of evaluation of logical operators is –
first NOT
then AND
then OR
If there are parenthesis, then the expression in the parenthesis
is evaluated first.

13. Qs. Create a truth table for the Boolean expression –
F = A.B’+ C
Steps-
1. In the given expression, there are three variables – A, B & C
2. Draw three columns for each possible input variable
combination and three columns for each of the logical
expression given – NOT, OR & AND
3. Since there are three variables, we have 23 = 8 rows

14. A B C Create a three column table,
we will add some more
columns.

15. A B C
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
Enter appropriate values into
the input variables.

16. A B C B’ A.B’ A.B’+C
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
Add columns B’, A.B’, A.B’+ C

17. A B C B’ A.B’ A.B’+C
0 0 0 1
0 0 1 1
0 1 0 0
0 1 1 0
1 0 0 1
1 0 1 1
1 1 0 0
1 1 1 0
Evaluate value for B’

18. A B C B’ A.B’ A.B’+C
0 0 0 1
0 0 1 1
0 1 0 0
0 1 1 0
1 0 0 1
1 0 1 1
1 1 0 0
1 1 1 0
Evaluate value for A . B’

19. A B C B’ A.B’ A.B’+C
0 0 0 1 0
0 0 1 1 0
0 1 0 0 0
0 1 1 0 0
1 0 0 1 1
1 0 1 1 1
1 1 0 0 0
1 1 1 0 0
Put values for A . B’

20. A B C B’ A.B’ A.B’+C
0 0 0 1 0
0 0 1 1 0
0 1 0 0 0
0 1 1 0 0
1 0 0 1 1
1 0 1 1 1
1 1 0 0 0
1 1 1 0 0
Finally, evaluate the value for A . B’+ C

21. A B C B’ A.B’ A.B’+C
0 0 0 1 0 0
0 0 1 1 0 1
0 1 0 0 0 0
0 1 1 0 0 1
1 0 0 1 1 1
1 0 1 1 1 1
1 1 0 0 0 0
1 1 1 0 0 1
Finally, evaluate the value for A . B’+ C

22. A B C B’ A.B’ A.B’+C
0 0 0 1 0 0
0 0 1 1 0 1
0 1 0 0 0 0
0 1 1 0 0 1
1 0 0 1 1 1
1 0 1 1 1 1
1 1 0 0 0 0
1 1 1 0 0 1
Finally, the solution for F = A . B’+ C

23. RULES REVISITED
While evaluating Boolean expression the rules which is required
to be followed are –
a) Evaluate the Boolean expression from
left to right ->
b) Evaluate the Boolean expression in the
parenthesis / brackets first
c) Perform all NOT expression
d) Perform all AND expression
e) Perform all OR expression