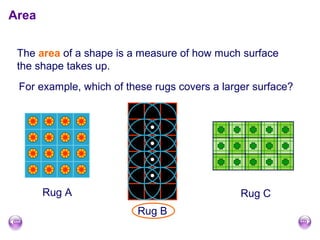
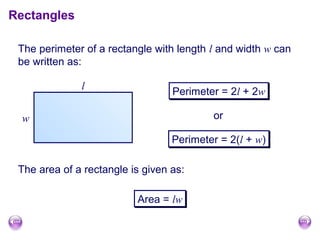
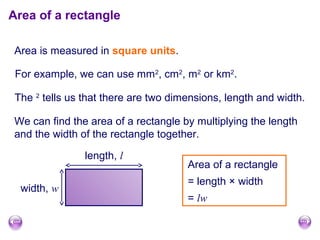
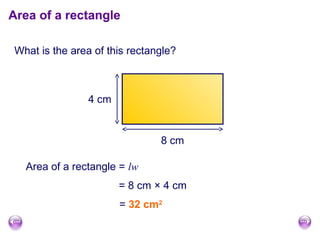
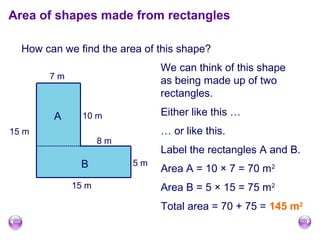
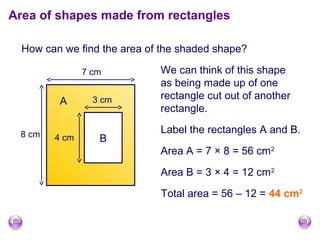
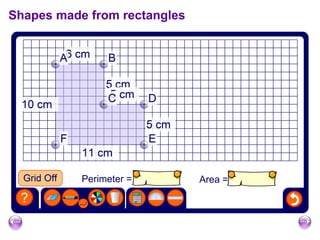
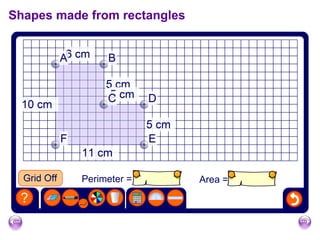
The document discusses calculating the area and perimeter of rectangles and shapes made from rectangles. It defines area as a measure of surface covered and perimeter as the distance around a shape. It provides the formulas for calculating the perimeter and area of rectangles as well as squares, which are special rectangles where the length and width are equal. It also explains how to find the total area of shapes made up of multiple rectangles by calculating the individual areas and summing them.