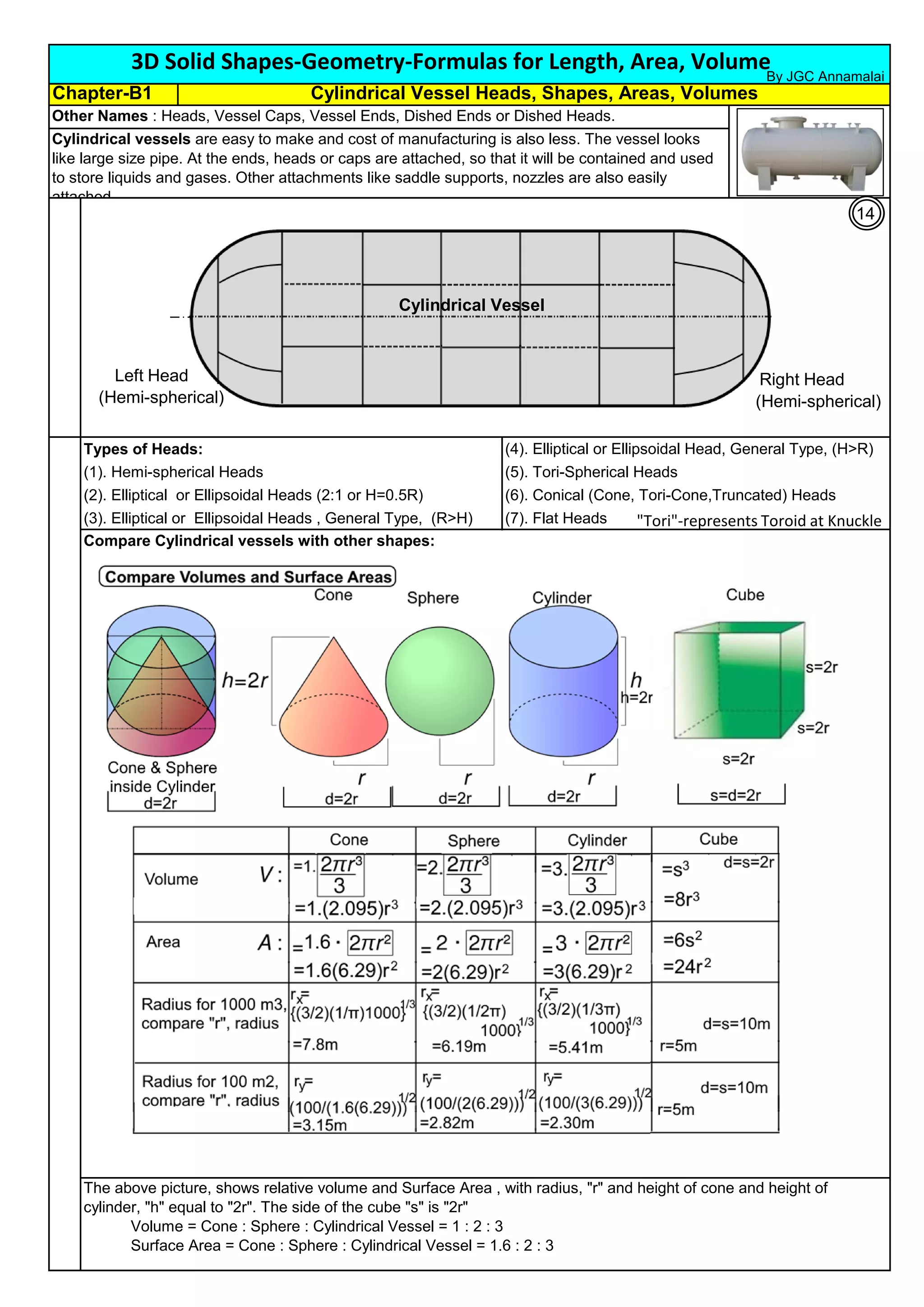
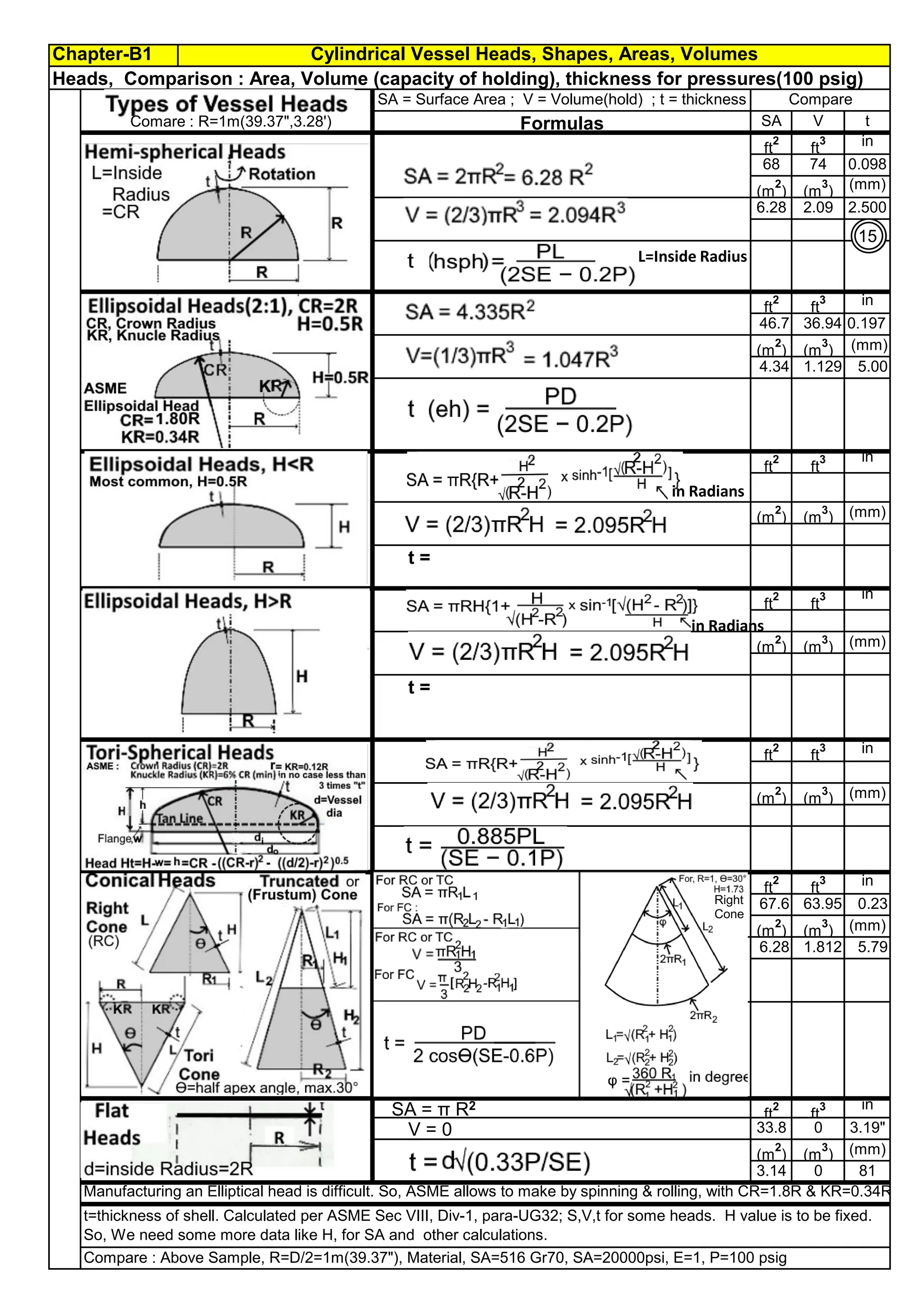
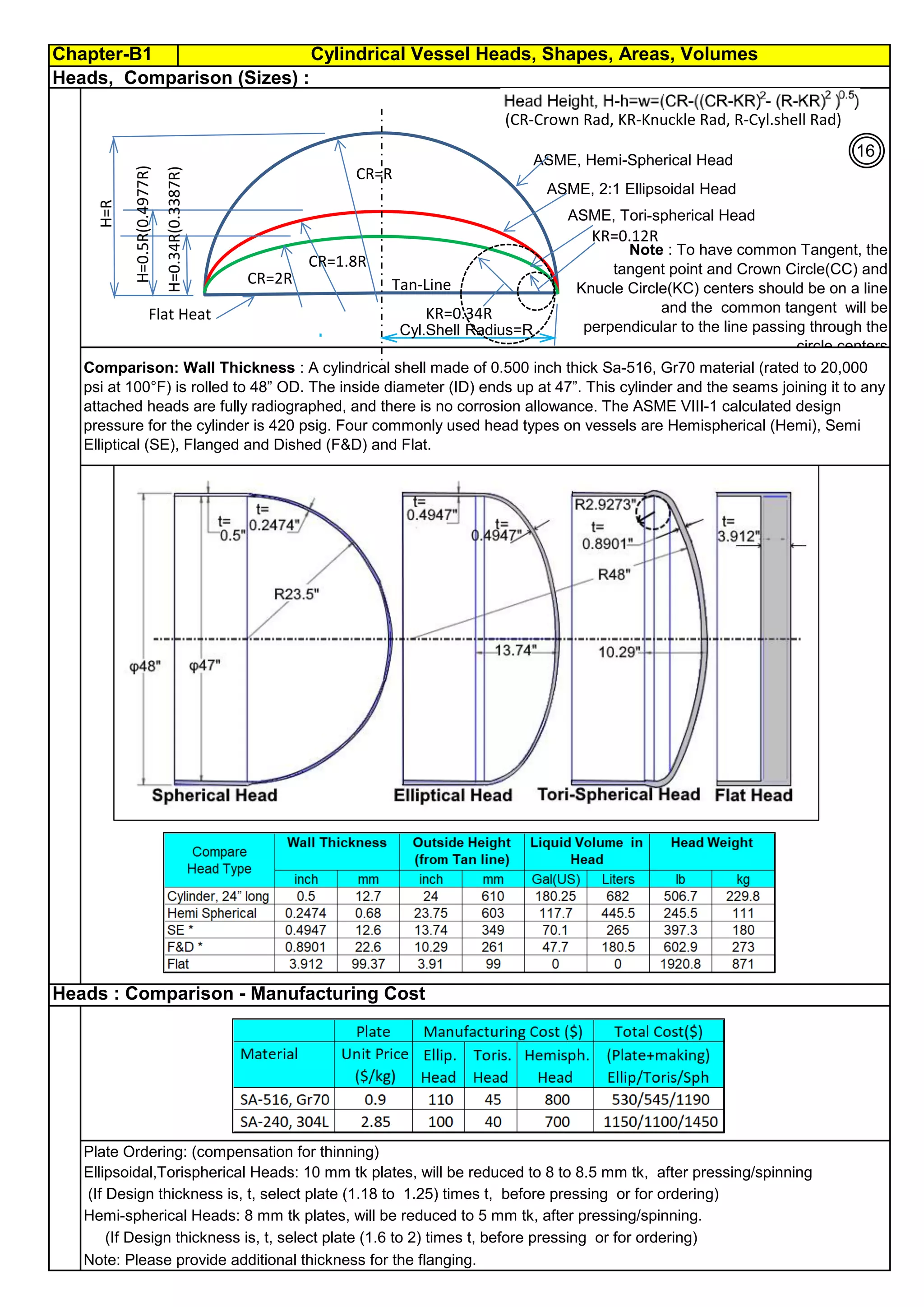
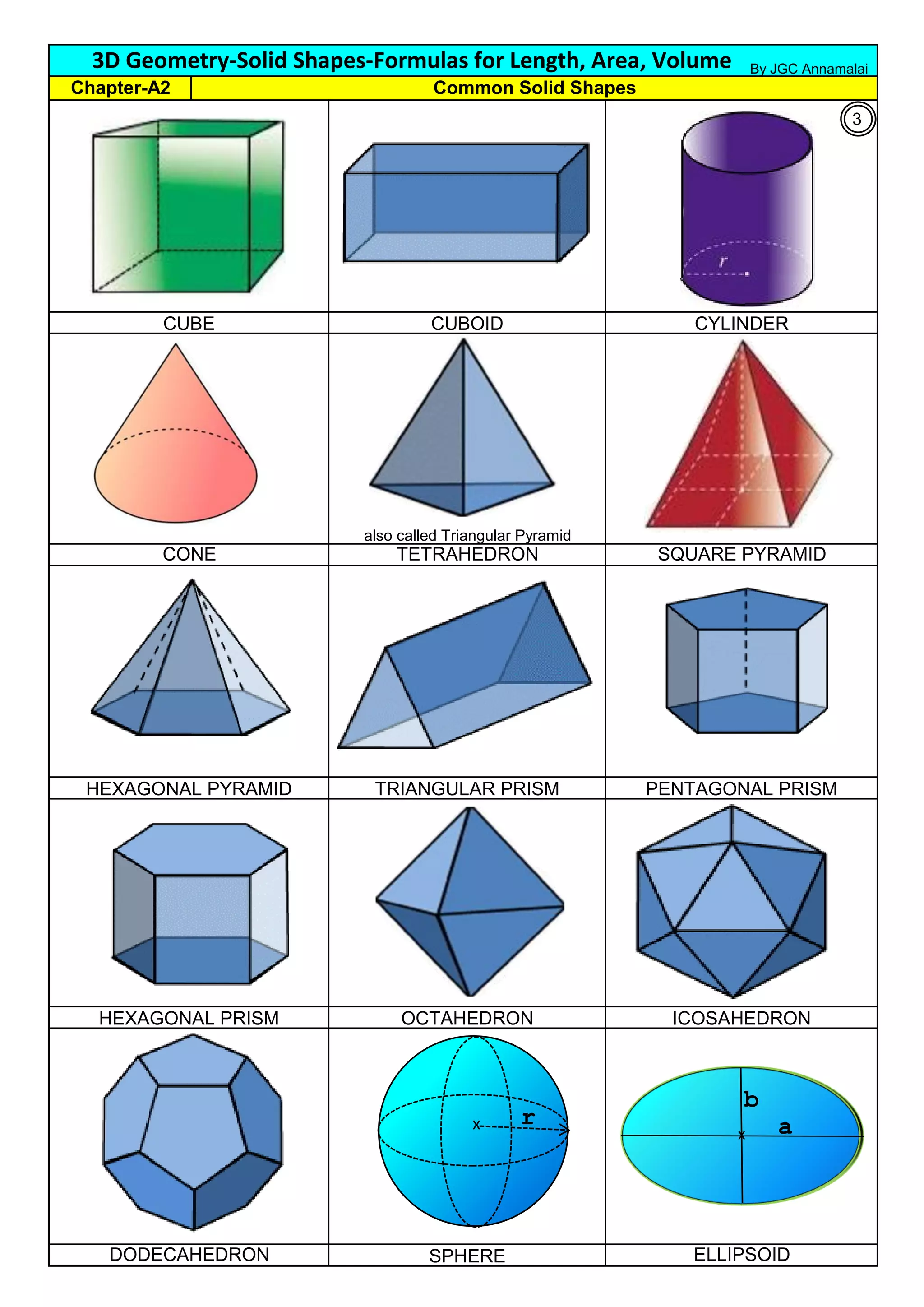
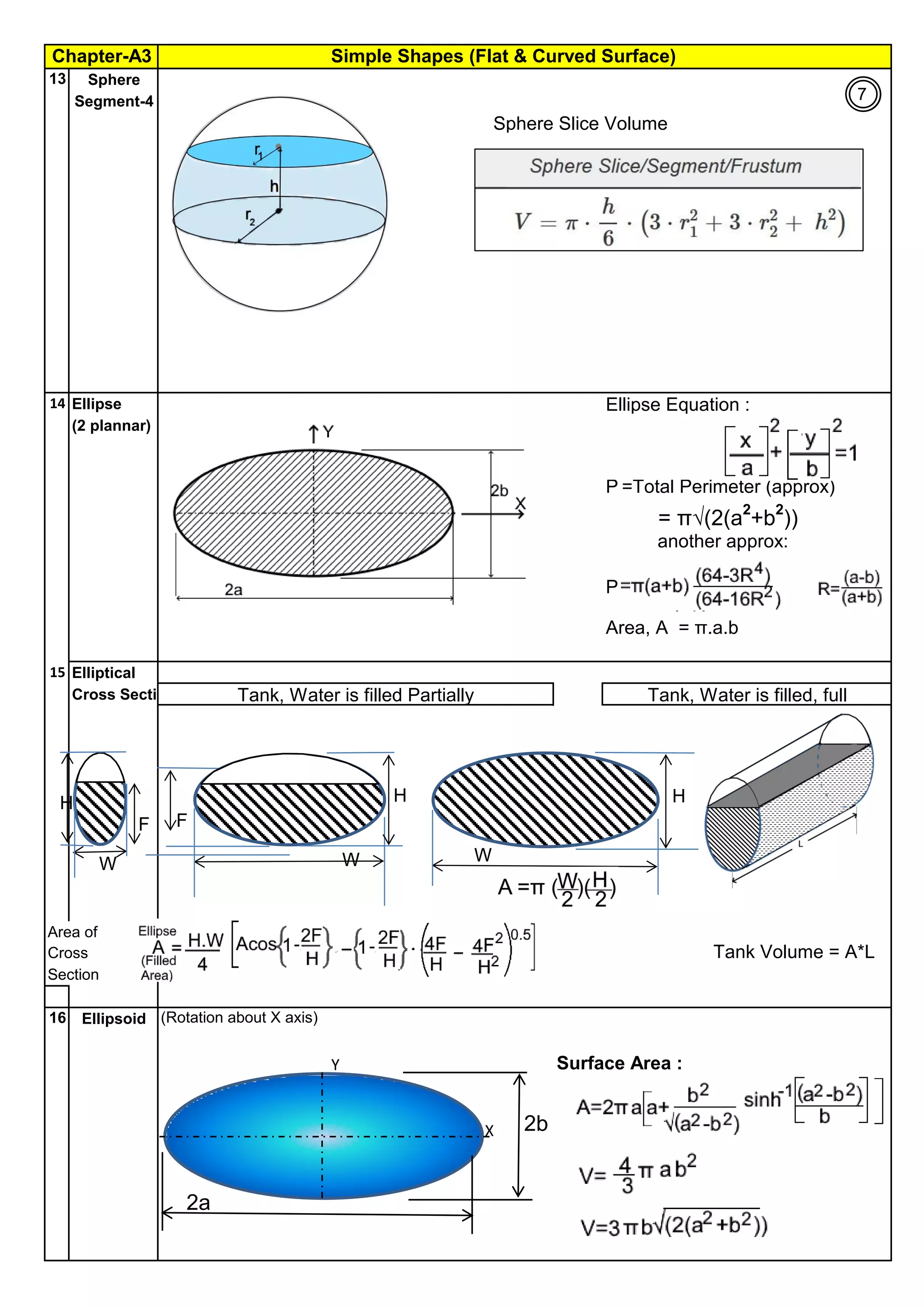
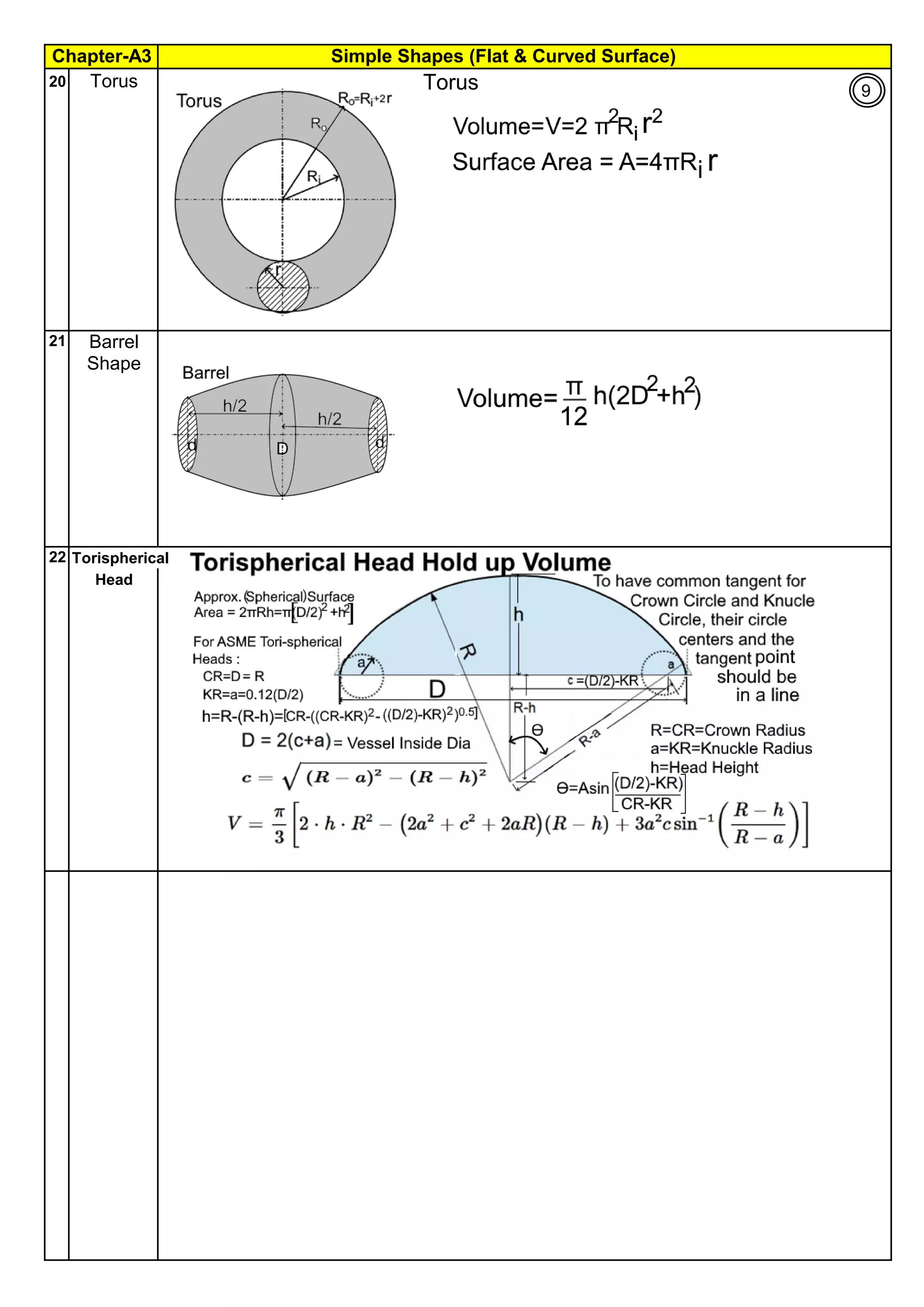
The document provides comprehensive formulas and explanations for calculating length, area, and volume of various 3D solid shapes, including cubes, cylinders, cones, spheres, and pyramids. It covers geometric properties, common solid shapes, and includes applications in real-world contexts such as cylindrical vessels and spherical tanks. Authored by R. Annamalai, the document serves as a detailed reference for understanding and applying geometric principles.

1. 1

2. 3D Solid Shapes, Geometry, Length, Areas, Volumes - Formulas
Formulas for 3D Solid Shapes, Geometry, Length, Areas, Volumes Page
(A1) Chapter List 2
(A2) Common Shapes 3
(A3) Simple Geometric Shapes - Length, Areas, Volumes 4
(A4) Line and its Family, Properties, Length, Angles, Areas 10
(A5) Triangle and its Family, Properties, Length, Angles, Areas 11
(A6) Conic Sections 12
(A7) Circle and its Family ; Properties, Length, Angles, Areas 13
Applications:
(B1) Cylindrical Vessel and its Heads 14
(B2) Spherical Tank, Sections, Manufacture 18
(B3) Helix, Helical Stairs, Manufacture of Helical Objects 23
Total Pages 25
Authored by R.Annamalai, (former Chief Equipment Engineer, JGC Corporation), rannamalai.jgc@gmail.com
Chapter-A1 (Topics) Chapter List
By JGC Annamalai
2

3. 3D Geometry-Solid Shapes-Formulas for Length, Area, Volume
CYLINDER
CUBOID
CUBE
Chapter-A2 Common Solid Shapes
ELLIPSOID
SPHERE
DODECAHEDRON
ICOSAHEDRON
OCTAHEDRON
HEXAGONAL PRISM
also called Triangular Pyramid
PENTAGONAL PRISM
TRIANGULAR PRISM
HEXAGONAL PYRAMID
SQUARE PYRAMID
TETRAHEDRON
CONE
By JGC Annamalai
r
x
x a
b
3

4. Length Distance between two points. Length may be straight length or curved length. Single or Two Dimensional
Units: mm, meter, km, inch, yard, mile
Area Flat or curved space occupied between straight lines, curved lines, Two or Three Dimensional
Units : sq.mm, sq.m, sq.km, hectare, sq.inch, sq.yard, sq.mile, Acre
Volume Space occupied, between flat & or curved areas; Volume=cross section*height; Three Dimensional
Units: cu.mm, cu.m, cu.km, litre, cu.inch, cu.yard, cu.mile, ounce, gallon, barrel
Weight Weight = total volume * the density (the density, is found from Density Tables or Engineering Handbooks)
Units: kgf, lb, ton
1 Cube a = length of one side of Cube
f = length, on One face, corner to corner
f = √(a
2
+a
2
) = √2. a = 1.414.a
d = Cube, one corner to farthest corner
d = √{(√2a)
2
+ a
2
) = √3.a = 1.732.a
A = Total Surface Area = 6.a
2
V = Total Volume = a
3
2 Cuboid
l,h,w = length of a side of Cuboid
f = One face, corner to corner
f = √(l
2
+h
2
)
d = Cube, one corner to farthest corner
d = √(l
2
+h
2
+w
2
)
A = Total Surface Area = 2(lh+lw+hw)
V = Total Volume = l.w.h
3 Cylinder
r = Radius of the Cylinder
h = height of the Cylinder
A1 = Top & Bottom circular Area = 2(π.r
2
)
Volume of Slant Cylinders(shape) = A2 = Cylindrical Surface Area = 2.π.r.h
=Base Area(A1) * Vertical Height(h) A = Total Surface Area = 2.(π.r
2
)+2.π.r.h = 2.π.r(r+h)
Slant surface Area of the Shape-
to change from , vertical position Total Volume = π.r
2
.h
4 Cone
r = Radius of Bottom Circle
h = height of the Cone
S = Slant length
A1 = Bottom Circle Area = π.r
2
A2 = Cone Slant Surface Area = π.r.S
A2 = π.r.√(r
2
+h
2
)
Volume of Slant Cones = A = Total Surface Area = (π.r
2
)+π.r.√(r
2
+h
2
)
=Base Area(A1) * Vertical Height(h)
A = Total Surface Area = π.r(r+√(r
2
+h
2
))
Surface area of slant cones, to change
from vertical position V = Total Volume = (1/3).π.r
2
.h = (1/3) A1.h
3D Geometry-Solid Shapes-Formulas for Length, Area, Volume
Simple Shapes (Flat & Curved Surface)
Chapter-A3
By JGC Annamalai
4

5. Simple Shapes (Flat & Curved Surface)
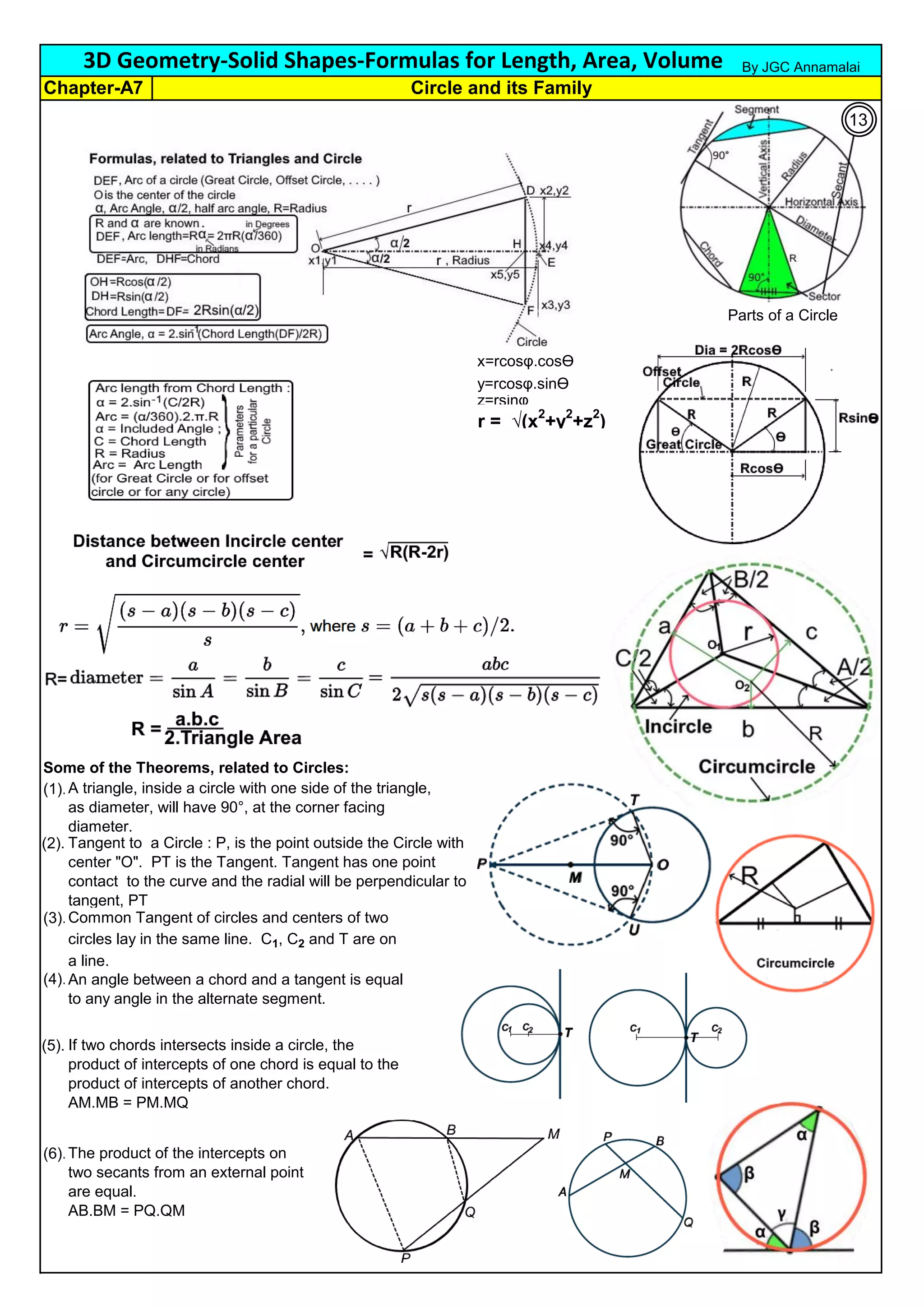
Chapter-A3
By JGC Annamalai
5 Tube
Pipe r1 = Outer Radius of the Tube;
Well Wall r2 = Inner of the Tube
h = height of the Cylinder
A1 = Top & bottom Ring Area = 2.π(r1
2
- r2
2
)
A2 =Outer Cylindrical Surface Area = 2.π.r1.h
A3 = Inner Surface Area = 2.π.r2.h
A = Total Surface Area
= 2.π(r1
2
- r2
2
)+2.π.h(r1+r2)
V1 = Total Volume = π.(r1
2
-r2
2
).h=π.(r1+r2)(r1-r2).h
V1 = 2π((r1+r2)(1/2)t.h)
"formula V2 = 2.π(r1+r2)(1/2).t.h, is the same
to V1, so, V2=V1"
6 Conical
Frustum r1 = Radius of Bottom Large Circle
r2 = Radius of the Top Small Circle
h = height of the Cone (truncated)
Truncated S = Slant length = √((r1 - r2)
2
+ h
2
)
Cone
A1 = Bottom Circle Area = π.r1
2
A2 = Top small Circle Area = π.r2
2
A3 = = π(r1 + r2)s = π(r1 + r2)√((r1 - r2)
2
+ h
2
)
A = π[ r1
2
+ r2
2
+ (r1 + r2) * √((r1 - r2)
2
+ h
2
) ]
V= Volume = (1/3)πh (r1
2
+ r2
2
+ (r1 * r2))
7 Pyramid
a = length of one side of Base of Pyramid
h = Height from base to the top
S1 = Slant Height = √(h
2
+(1/4)a
2
)
S2 = Corner Slant Height = √(h
2
+(1/2)a
2
)
A1 = Base Area = a
2
A2 = Lateral Surface Area = a√(a
2
+4h
2
)
A = Total Surface Area = A1+A2 = a
2
+ a√(a
2
+ 4h
2
)
(Also check at Chapter, Traiangles & Applications)V = Total Volume = (1/3)a
2
h = (1/3).A1.h
8 Sphere
r = radius of the Sphere
d = diameter of the sphere=2r
C = Circomference = 2π.r
A = Area of Sphere = 4πr
2
V = Total Volume = (4/3)π.r
3
5

6. Simple Shapes (Flat & Curved Surface)
Chapter-A3
By JGC Annamalai
9 Spherical
Segment-1 R = Radius of the Sphere
Cap D = Diameter of the sphere=2R
of Sphere h = Height of the Cap
a = Radius of the Cap Circle = √(h(2R - h))
C1 = Circumference of Sphere = 2π.R
C2 = Circumference of Base Circle = 2π√(h(2R - h))
C3 = Arc length(KLM) of Base Circle = 2π√(h(2R - h))
A1 = Base circle Surface Area = πa
2
= πh(2R - h)
A2 = Curved Surface Area = 2πRh = π(a
2
+ h
2
)
A = Total Surface Area = π(h(2R - h) + 2πRh
V = Cap Volume = (1/6)πh(3a
2
+ h
2
)
V = Volume = (1/3)πh
2
(3R - h)=πh((1/2)a
2
+ (1/6)h
2
)
Liquid Volume, in the Sphere Tank, below level, "h"
= V(Spherical Cup) =(4/3)πR
3
- (1/3)πh
2
(3R - h)
10 Spherical R = Radius of the Sphere=
Segment-2 =√{ [ [(a-b)2 + h2] [(a+b)2 + h2] ] / 4h2 }
D = Diameter of the sphere=2R
h = Height of the Segment
a = Radius of segment bottom Circle = √(k+h)(2R - (k+h))
b = Radius of Segment top Circle = √(k(2R - k)
C1 = Circumference of Sphere = 2π.R
C2 = Circumference of top Base Circle = 2π√(h(2R - h))
C3 = Arc length(KLM) of Base Circle =
A1 = Bottom Base circle Surface Area = πa2
= π((k+h)(2R - (k+h))
x2
+y2
=R2
x1=a, y1= √(R2
-a2
) A3 = Curved Surface Area = 2πRh
x2=b y2= √(R2
-b2
) A = Total Surface Area = A1+A2+A3
find, h=y2-y1 V = Volume = (1/6)πh(3a
2
+3b2+h
2
)
V = Volume = (1/3)πh
2
(3R - h)
11 Spherical
Segment-3 C = Circomference = 2π.R(ϴ/360)
(Spherical (at equator)
Wedge) A = Area of Spherical = 4πR
2
(ϴ/360)
surfa
As=Surface at the two Sides=πR
2
V = Total Volume = (4/3)π.R
3
(ϴ/360)
12 Spherical
Segment-4 C = Circomference = 2π.R(ϴ/360)
(Spherical (at equator)
Sector) A =Total Surface Area = πR(2H+(C/2))
V = Total Volume = (2/3)π.R
2
.H
C=2(H(2R-H))
0.5
6

7. Simple Shapes (Flat & Curved Surface)
Chapter-A3
By JGC Annamalai
13 Sphere
Segment-4
Sphere Slice Volume
14 Ellipse Ellipse Equation :
(2 plannar)
P =Total Perimeter (approx)
= π√(2(a2
+b2
))
another approx:
P
Area, A = π.a.b
15 Elliptical
Cross Section
Area of
Cross Tank Volume = A*L
Section
16 Ellipsoid (Rotation about X axis)
Surface Area :
Tank, Water is filled, full
Tank, Water is filled Partially
X
Y
2a
H
W
F
W
H
2b
H
W
F
7

8. Simple Shapes (Flat & Curved Surface)
Chapter-A3
By JGC Annamalai
17 Ellipsoid Ellipsoid
Spheroid
Spheroid - Looks like a sphere tank, but the height is 0.5 to 0.75 times shorter than spherical height
Ellipsoid - A shape obtained by revolving a half Ellipse, about one of its axis.
Ellipsoid
a,b,c
X,Y,Z axis
Perolate
Spheroid
c=b
Rotation about, X-axis
Oblate
Spheroid
c=a
Rotation about, Y-axis
18 Parabola
Total Area of Convex Surface of a Parabola
(Segment COD)
Paraboidal Volume, between slice AB and CD
Paraboidal Volume, between two slices, at O and CD
19 Hyperbola
Volume , bound by segment, AOB
Surface Area Volume
Shape
Examples : Hanging rope ends tied to a horizontal pole, also called a catenary,
(y = b+a (cosh (x/a))); Gateway Arch, St. Louis, USA, Diving from swimming pool
platform, sky diving from airplane, (y = A*ln (cosh Bt))
c
c
b
b
a
a
c
c
b
b
Spheroid
X
Y Y
Z
8

9. Simple Shapes (Flat & Curved Surface)
Chapter-A3
By JGC Annamalai
20 Torus Torus
21 Barrel
Shape
22 Torispherical
Head
9

10. 3D Geometry-Solid Shapes-Formulas for Length, Area, Volume
Chapter-A4
Straight Lines m is the slope of the line to X axis
(1).Simple line equation, C is the point of cut of the line on Y axis, when x=0
(2).Two Coordinates and line equation
(3).Angles between 2 lines, tanϴ=(m2 - m1)/(1 + m1.m2)
with slopes, m1 and m2
(4).Lines are parallel, m1=m2
(5).Lines are perpendicular, m1.m2= -1
Curved Lines:
We find, curves for Helix, spiral, cycloid etc and exponential curve, etc
Trignometric function curves: some curve follow sine, cosine, tangent curve
Hyperbolic function curves: sinh, cosh, tanh etc have standard curves.
Often curves are changed to straight line, taking lograthmic functions or logrithmic scales.
More curves can be found in : "List of curves" https://en.wikipedia.org/wiki/List_of_curves#Degree_1
Curve Fitting : There are many curves or part of the curve and they do not fall in the above category.
Often empirical equations and curves are fixed for such cases.
(3). Parabola: A parabola is a curve where any point is at an equal distance from: a fixed point (the focus ), and. a fixed
straight line (the directrix )
We see in daily life, the data(like personnel blood pressure, atmospheric temperature, rain fall, metal price etc)are
continuously changing. Often it is required to make the equation of the line to analyse or to interprete or to forecast. If
the data is changing widely, the bumped or irregular curve is broken in to many segments and analyzed.
(2). Ellipse: The ellipse has two center points. Ellipse is a curved line, the locus point is at
a distance such that the sum of arm distance from the first center point and the arm
distance from second center point are constant.
(1). Circle: Circle has a single center point. Circle is a curved line, the locus point is moving
with a constant radius & with a constant center point.
(4). Hyperbola: A hyperbola is an open curve with two branches, the intersection of a plane with both halves of a double
cone. The plane does not have to be parallel to the axis of the cone; the hyperbola will be symmetrical in any case.
Line and its Family
y =mx+C
Y
X
(x1,y1)
(x2,y2)
ϴ
C
(x,y)
By JGC Annamalai
ϴ
90°
ϴ ϴ
R
C1 C2
R1
R2
R1+R2=Constant
10

11. 3D Geometry-Solid Shapes-Formulas for Length, Area, Volume
Chapter-A5
Trianges : Area
(a). Right Angle triangle & inside vertical
Area = (1/2)b.h
(b). Known: 1 side and 2 angles. Angle A+B+C=180°
a=b.sinA/sinB
R = Circumcircle, radius
(b). Known : 2 sides and included angle to one
Area = (1/2)a.b.sinϴ = 2R
2
sinA.sinB.sinC
(c). Known, 3 sides, a, b, c
Area = √((s(s-a).(s-b).(s-c)) s=(1/2)(a+b+c)
(d). Known: x,y co-ordinates for the three corners of a Triangle.
A = (1/2)[x1(y2–y3)+x2(y3–y1)+ x3(y1–y2)]
Base Polygons
(Equal Sides)
R=(a/2).(1/SIN(ϴ/2) ht=R.COS(ϴ/2) P=N.a AB=N.(1/2).a.h
[N];[ϴ];[ϴ/2] 3 120 2.1 1.0 4 90 1.6 0.8 5 72 1.3 0.6 6 60 1.0 0.5 8 45 0.8 0.4 12 30 0.5 0.3
a : 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
R 0.6 1.2 1.7 2.3 0.7 1.4 2.1 2.8 0.8 1.7 2.5 3.4 1 2 3 4 1.3 2.6 3.9 5.2 1.9 3.9 5.8 7.7
ht 0.3 0.6 0.9 1.2 0.5 1 1.5 2 0.7 1.4 2.1 2.7 0.9 1.7 2.6 3.5 1.2 2.4 3.6 4.8 1.9 3.7 5.6 7.5
P 3 6 9 12 4 8 12 16 5 10 15 20 6 12 18 24 8 16 24 32 12 24 36 48
AB 0.4 1.7 3.9 6.9 1 4 9 16 1.7 6.9 15 27 2.6 10 23 42 4.8 19 43 77 11 45 101 179
Triangle is the base shape to calculate the area. Ancient Greeks used the Trigonometry to find area of complicated
shapes. Sin-Cos-Tan etc of a triangle, are the result of their research and developments. Even today, most of the
complicated shapes are split in to number of triangles and their sides are measured and areas are calculated. Triangles are
the major tool of modern Land Surveyors.
Triangle and its Family
Value➔
N=number of sides of polygon ; a=base side size; R=Outer Radius of Polygon; P=Perimeter;
ϴ=one side of polygon-triangle, included angle; ht=vertical from center to side; AB=Area of Base
a=2R.SIN(ϴ/2)
ϴ=(360/N) or =(2π/N)
A,B,C are Angles. a,b,c are sides. As
a convention, the angle, facing the
side "a" is called Angle "A"
a
b
c
90°
c
a
b
(x1,y1) (x2,y2)
(x3,y3)
h
ϴ R
R
R
R
R
R
ϴ h
a a
a
a
a
Outer
Circle
Triangles : Trigonometry :
Number of Sides of Polygon
Inc. Angle, Degrees
Inc.Angle, Rad
Inc. Half Angle, Rad
By JGC Annamalai
11
a
b
c
C h A
B R

12. 3D Geometry-Solid Shapes-Formulas for Length, Area, Volume
Chapter-A6
Locus:
Suppose that, for some constant e, the equation, PF = ePM
• if e =0, then the curve is a circle; • if e = 1 then the curve is a parabola; and
• if 0 < e < 1 then the curve is an ellipse; • if e > 1 then the curve is a hyperbola.
Applications :
Circle : Circle is very common and well known object or shape. Their applications are everywhere in day to day life.
Let us have a straight line, called the directrix, and a fixed point, called the focus. If
we have another point, P, then we can consider the perpendicular distance of P
from the line(PM), and also the distance of P from the focus(PF). We will get
varaity of curves, as shown below.
The constant "e" is called the “eccentricity” of the conic. It can be shown that these definitions are equivalent to the
definitions given in terms of sections of a cone.
Ellipse : On Conic section, well known next to circle, is Ellipse. Many of the building arches are in the shape of ellipse.
Some of the well known ellipses are : Orbit of Earth and other planet, revolving our Sun; Taj Mahal main hall; US
President's White House
Park-South or Ellipse;
Parabola : San Fransico's Golden Gate Bridge, SS Gateway Arch, St.Louis, Catenary, Part of the track of kicked foot
ball in sky, trajectory of a stone thrown in the sky, rocket escaping from Earth Gravity, orbit of some comets, Parabola
dish for communication and light and heat to focus or to reflect as coherent beam.
Hyperbola : LORAN : Long Range Navigation of Ships used to locate or measure
distance from 2 places. Some comets follow the hyperbolic curve. Hyperbolic /
triconometric curves are in hyperbolic shapes.
Conic Sections
Conic Sections : In mathematics, a conic section (or simply conic) is a curve obtained as the intersection of the surface
of a cone with a plane. The four types of conic section are (1). circle, (2). ellipse, (3). parabola and (4). hyperbola.
It is also defined as a locus / trajectory of a point, with conditions for different shapes.
is always true. All the points “P” satisfying this equation lie on a curve called the “locus”. We shall
see that we get curves of particular types, depending upon the value of the constant, "e":
A Circle is obtained when a section,
through a horizontal plane like, E-E cut
An ellipse is obtained when a section plane
A –A , inclined to the axis
A parabola is obtained when a section
plane B –B , parallel to one of the generators
cuts the cone, including base of the cone.
A hyperbola is obtained when plane C –C ,
inclined to axis cone on one side of the axis.
A rectangular hyperbola is obtained when
a plane D –D , parallel to axis cuts the cone.
By JGC Annamalai
12

13. 3D Geometry-Solid Shapes-Formulas for Length, Area, Volume
Chapter-A7
x=rcosφ.cosϴ
y=rcosφ.sinϴ
z=rsinφ
r = √(x
2
+y
2
+z
2
)
Some of the Theorems, related to Circles:
(1).
(2).
(3).
(4).
(5).
(6).
Circle and its Family
A triangle, inside a circle with one side of the triangle,
as diameter, will have 90°, at the corner facing
diameter.
An angle between a chord and a tangent is equal
to any angle in the alternate segment.
If two chords intersects inside a circle, the
product of intercepts of one chord is equal to the
product of intercepts of another chord.
AM.MB = PM.MQ
The product of the intercepts on
two secants from an external point
are equal.
AB.BM = PQ.QM
Tangent to a Circle : P, is the point outside the Circle with
center "O". PT is the Tangent. Tangent has one point
contact to the curve and the radial will be perpendicular to
tangent, PT
Common Tangent of circles and centers of two
circles lay in the same line. C1, C2 and T are on
a line.
By JGC Annamalai
Parts of a Circle
13

14. Types of Heads: (4). Elliptical or Ellipsoidal Head, General Type, (H>R)
(1). Hemi-spherical Heads (5). Tori-Spherical Heads
(2). Elliptical or Ellipsoidal Heads (2:1 or H=0.5R) (6). Conical (Cone, Tori-Cone,Truncated) Heads
(3). Elliptical or Ellipsoidal Heads , General Type, (R>H) (7). Flat Heads
Compare Cylindrical vessels with other shapes:
Cylindrical Vessel Heads, Shapes, Areas, Volumes
Chapter-B1
3D Solid Shapes-Geometry-Formulas for Length, Area, Volume
The above picture, shows relative volume and Surface Area , with radius, "r" and height of cone and height of
cylinder, "h" equal to "2r". The side of the cube "s" is "2r"
Volume = Cone : Sphere : Cylindrical Vessel = 1 : 2 : 3
Surface Area = Cone : Sphere : Cylindrical Vessel = 1.6 : 2 : 3
Cylindrical vessels are easy to make and cost of manufacturing is also less. The vessel looks
like large size pipe. At the ends, heads or caps are attached, so that it will be contained and used
to store liquids and gases. Other attachments like saddle supports, nozzles are also easily
attached.
Other Names : Heads, Vessel Caps, Vessel Ends, Dished Ends or Dished Heads.
Normally, cylindrical vessels are easy to make. Cost of construction is also less.
Left Head Right Head
"Tori"-represents Toroid at Knuckle
Cylindrical Vessel
(Hemi-spherical)
(Hemi-spherical)
By JGC Annamalai
14

15. Cylindrical Vessel Heads, Shapes, Areas, Volumes
Chapter-B1
By JGC Annamalai
Heads, Comparison : Area, Volume (capacity of holding), thickness for pressures(100 psig)
SA V t
ft
2
ft
3 in
68 74 0.098
"
(m
2
) (m
3
) (mm)
6.28 2.09 2.500
ft
2
ft
3 in
46.7 36.94 0.197
"
(m
2
) (m
3
) (mm)
4.34 1.129 5.00
ft
2
ft
3 in
(m
2
) (m
3
) (mm)
t =
ft
2
ft
3 in
(m
2
) (m
3
) (mm)
t =
ft
2
ft
3 in
(m
2
) (m
3
) (mm)
ft
2
ft
3 in
67.6 63.95 0.23
(m
2
) (m
3
) (mm)
6.28 1.812 5.79
ft
2
ft
3 in
V = 0 33.8 0 3.19"
(m
2
) (m
3
) (mm)
3.14 0 81
Formulas
SA = Surface Area ; V = Volume(hold) ; t = thickness Compare
Compare : Above Sample, R=D/2=1m(39.37"), Material, SA=516 Gr70, SA=20000psi, E=1, P=100 psig
t=thickness of shell. Calculated per ASME Sec VIII, Div-1, para-UG32; S,V,t for some heads. H value is to be fixed.
So, We need some more data like H, for SA and other calculations.
Manufacturing an Elliptical head is difficult. So, ASME allows to make by spinning & rolling, with CR=1.8R & KR=0.34R
L=Inside Radius
in Radians
in Radians
SA = π R2
Right
Cone
Comare : R=1m(39.37",3.28')
15

16. Cylindrical Vessel Heads, Shapes, Areas, Volumes
Chapter-B1
By JGC Annamalai
Heads, Comparison (Sizes) :
(CR-Crown Rad, KR-Knuckle Rad, R-Cyl.shell Rad)
Flat Heat
Heads : Comparison - Manufacturing Cost
Plate Ordering: (compensation for thinning)
Ellipsoidal,Torispherical Heads: 10 mm tk plates, will be reduced to 8 to 8.5 mm tk, after pressing/spinning
(If Design thickness is, t, select plate (1.18 to 1.25) times t, before pressing or for ordering)
Hemi-spherical Heads: 8 mm tk plates, will be reduced to 5 mm tk, after pressing/spinning.
(If Design thickness is, t, select plate (1.6 to 2) times t, before pressing or for ordering)
Note: Please provide additional thickness for the flanging.
Note : To have common Tangent, the
tangent point and Crown Circle(CC) and
Knucle Circle(KC) centers should be on a line
and the common tangent will be
perpendicular to the line passing through the
circle centers
Comparison: Wall Thickness : A cylindrical shell made of 0.500 inch thick Sa-516, Gr70 material (rated to 20,000
psi at 100°F) is rolled to 48” OD. The inside diameter (ID) ends up at 47”. This cylinder and the seams joining it to any
attached heads are fully radiographed, and there is no corrosion allowance. The ASME VIII-1 calculated design
pressure for the cylinder is 420 psig. Four commonly used head types on vessels are Hemispherical (Hemi), Semi
Elliptical (SE), Flanged and Dished (F&D) and Flat.
H=R
H=0.5R(0.4977R)
H=0.34R(0.3387R)
ASME, Hemi-Spherical Head
ASME, 2:1 Ellipsoidal Head
ASME, Tori-spherical Head
CR=R
CR=1.8R
CR=2R
KR=0.34R
KR=0.12R
Tan-Line
Cyl.Shell Radius=R
16

17. Cylindrical Vessel Heads, Shapes, Areas, Volumes
Chapter-B1
By JGC Annamalai
Calculate Liquid Volume inside a Horizontal Cylindrical Vessel
17

18. Chapter-B2
Other Names : Ball Tanks, Spheres, Horton Sphere; Spheroids(flattened or Spheres pressed vertically),
Advantage of using Spherical Tank as a Storage Vessel :
(1)
(2)
(3)
(4)
Disadvantages are :
(1)
(2)
.
(3)
Spherical Tank Sections:
(1)
.
3D Geometry-Solid Shapes-Formulas for Length, Area, Volume
Compared to Bullet Tank: In case of maintenance of sphere, the whole sphere has to be shut
down. Money wasted, due to the shut down. In case of bullet tanks (one sphere tank
olume=many bullet tanks), one bullet tank can be made as stand-by or spared or shared.
In case, sphere has repairs, uneconomical to do or abandoned or moved to another location,
it it is difficult to move sphere.The Sphere is cut into pieces, for transport and rewelded. It is
far cheaper to make a new sphere. Due to this, resale value of sphere tank is very less.
Sphere is one of the most common shapes known to man. The Earth, most of the planets, eye ball, Galaxy spins etc
have spherical shapes. Spheres are used as LPG and LNG or liquid-gas storage vessels.
Spherical tanks are preferred choice by the users for the LPG, and other petroleum liquids and gases(ethane,
methane, poly-propylene etc). With uniform Surface tension, Water drops, has near spherical shape. With their unique,
entirely rounded profile, spheres allow for efficient, large volume storage of compressed gases in a liquid stage. Most
of the gases(like Butane, Propane etc), when pressed, on cooling, they will change to liquids.
One of the most significnt benefits of using spherical storage tanks is the ability to hold very large liquid volumes within
a proportionally small amount of space. The ‘footprint’/area needed for a sphere is considerably smaller than that
needed for the number of storage bullets required to accommodate an equivalent volume.
Spherical Tank, Planes, Plate Arrangement, Marking, Manufacture
Spherical tanks are preferred as the surface area the vessel / unit volume is least, among other shapes like cylinder,
square, ellipsoids etc. So, heat transfer is less. The service fluid will not be cooled or heated fast.
As the surface area is least, heat inside the tank, will be maintained for longer times, comparing to other storage
vessels. Cost of painting, coating, insulating cost per unit volume is less
As a pressure vessel, spherical tanks have the least thickness for the same diameter and pressure, so the weight of
the vessel/unit volume stores is less. Cost of plates per unit volume of storage is less
Shop Fabrication & Installation : Lead time for bullet tanks, are typically in the 2-3 months range. Lead time for
spherical tank, required for fabrication/construction, which can be up to 12 -18 months in some cases. Due to
transportation limitations, these large vessels must be fabricated in sections off-site and then assembly completed in
the field. The process requires significant time and coordination to ensure proper staging, sequence of assembly and
welding—with continual on-site QC & testing throughout the on-site construction process.
Most of the Sphere Tank Plates are grouped, pressed, marked and cut either as Equator, Temperate or Polar Plates.
Plates are cut in the following Planes : (a). Horizontal Plane, Plane,is horizontal and pass through Sphere Center, (b).
Vertical Plane, passing through the Sphere Center, (c). Inclined Plane, inclined to sphere center axis, passing
through the Sphere Center. (d). Offset Plane, A horizontal plane offset to Sphere center,
By JGC Annamalai
18

19. Chapter-B2 Spherical Tank, Planes, Plate Arrangement, Marking, Manufacture
(2)
(3)
.
Formulas used in the Sperical Tank Plate Cutting Calculations:
Basic Methametical (Tricnometry and Co-ordinate) Formulas are used in Sphere Tank Calculations:
V=(4/3)πR3
= 1000m
3
R=((7/22)*(3/4)*V)0.333
R=6.194m, D=12.388»12.4m
N= π.D/w=(22/7)(10000)/2000
N=15.714 » 16
Number of Column (C)
C=N/2=16/2=8
through the center :
A sample plate sectioning for a medium size tank is
shown below:
Sections: Spherical Tank sectioning is often explained with an orange peel or an apple sections. Some of the Orange
peels are shown above for easy understanding. The peeled skin is often called a petal. The orange is made of many
segments. Segments are also called Spherical Crescent or Spherical Wedge.
Spherical Tanks are used to store liquids / gases (mostly volatile products) like: Gasoline, Anhydrous Ammonia, Vinyl
Chloride Monomer (VCM), Naphtha, Butane, Propane, Propylene. Cryogenic Tanks for Ethane, NGL(Methane),
Butadiene, Ethylene, Hydrogen, Oxygen, Nitrogen, Helium and Argon gases.
Sections / plate cutting used in most of the sphere making is shown,below. Formulas used in the calculation for plate
marking, cutting is also shown below.
Most nearest, best arrangement of plates are, Equator-
Temperate-Polar Plates, as shown here.
Offset Circle: Circle at the Offset plane. It is always
smaller than Great circle. Some people call, "offset
circle" as "minor circle".
Angle subtended by each equator plate, at Horizontal
plane,
Assume plate available width, or press column spacing,
2m, Inside Diameter, D of sphere is 12.4m.
Number of columns: The sphere diameter(D), is selected based on the
total storage capacity required by the Plant. From capacity, diameter is
selected. Based on the availability of width of the plates of the required
ASTM material, Number of plates(N) at the equator (D=Diameter of the
vessel, w=width of the plate). Normally, equator plates are fixed in
multiples of 4.
Horton Sphere is Trade Name after its founder, Horace Ebenezer Horton. First field installed sphere was made around
1923. CBI is the present name of the company and CBI had constructed more than 3500 Spherical Tanks, around the
world. That includes
(a). liquid spheres up to 94 feet (28.6 m) in diameter
(b). gas spheres up to 110 feet (33.5 m) in diameter
(c). world’s largest self-supporting sphere, measuring 225 feet (69 m) in
diameter nuclear plant containment vessel in New York
Great Circle = Circle , cut by a plane, that plane is
passing through the center of sphere. OD(Great Circle) =
Sphere Diameter
For marking & cutting, we take the inside diameter as the
reference
Often, min. 8 point on one side of sphere plate is
marked. Initially, manual marking is done. You may use,
template, fish bone or similar tools, for repeat jobs and
for speed work.
The following pages, give different sizes of spheres and
their plate arrangement. Formulas used to mark different
types of plates(Equator-Temperate-Polar) are also given.
Pressed and spherical curvature checked and QC
accepted plates are taken up for marking.
Sphere Sections
Spheres with Diameters, 22m and above, normally
need, full sphere PWHT, after welding.
Parts of a Circle
ϴ=360/N = 360/16=22.5°
19

20. Chapter-B2 Spherical Tank, Planes, Plate Arrangement, Marking, Manufacture
Sphere Cutting Planes : For simplicity and for easy calculation of Arc and Chord for fabrication, we follow:
(a). Horizontal Plane :
Plane,is horizontal and pass through Sphere Center,
(b). Vertical Plane :
Equator plate sides are cut with vertical
planes, passing through the Sphere Center,
(c). Inclined Plane :
Plane inclined to sphere center axis
and passing through the Sphere Center.
Polar plates and temperate plates are cut
with inclined plane cutting
ABCO1 is horizontal plane. O1 is sphere center. ABC is the great circle
DEFO2 is the offset Plane, O2 is the center for offset circle DEF.
DGFO1 is the inclined plane, O1 is the center of sphere.
(d). Offset Plane :
A horizontal plane, are offset to
Sphere center
(e). Co-ordinates.
Equation of a sphere (with x=rcosφ.cosϴ
center: 0,0,0) x2
+y2
+z2
=R2
y=rcosφ.sinϴ
Equation of a sphere(with center:a,b,c)z=rsinφ
(x-a)2
+(y-b)2
+(z-c)2
=R2
r = √(x
2
+y
2
+z
2
)
It is the base plane for calculation.
We assume , it is horizontal. The
outer circle is the Sphere radius and
all sphere Radii and Diameters are
called Great Circle radii and
diameters.
Equator plates, arcs at the Horizontal
Plane are calculated, by: (N is the
number of plates and α is the
included angle of vertical planes).
Most of the equator plates are cut with vertical plane cutting.
Some sides of temperate plates have vertical plane cutting
α=360/N = 360/16=22.5°
20

21. Chapter-B2 Spherical Tank, Planes, Plate Arrangement, Marking, Manufacture
21

22. Chapter-B2 Spherical Tank, Planes, Plate Arrangement, Marking, Manufacture
22

23. Helix is the locus of a horizontally moving point on a rotating horizontal cylinder, at a fixed speed.
Spiral is the locus of a point(in space), tied to a rod end and the rod revolves on a cylinder..
Examples of spiral : The snail shell, spiral spring, mainly used in Clock and instruments, vortex on a moving fluid.
Some of the definitions are: R= Radius of Helix
Helix Angle = α = tan-1(H/L)=tan
-1
(360*H/(2πRφ))
Calculate, Helix angle & L, for R=2000, H=1600, φ=90°H= The Pitch or Head
α = tan-1(1600*360/(2π2000ϴ)), α = 0.471rad=26.99° L= √{(2πR(φ/360))
2
+H2
}
Helical Curved Distance, at any point(L) on the Helix curve =
(φ, the horizontal component of the angle of the curve at any point on the Helix)
Hp = the Pitch Height
Hs = Stairs Height
(h, normal-200mm)
Number of Steps
N = Hs/h
steps=Going/tread,
= 250mm(common)
Stairs to Spherical Tanks: The following stairs are
most common in the Industry:
(1). Straight Strair + Helical Stair
(2). Straight Stair + U and L turn straight stairs
(3). Straight Stair up to the top Platform
(4). Helical Stair, from Ground level to top Platform
Examples of Hexlix are : Thread forming on a lathe machine. Thread forms on most of the bolts and nuts, pens &
bottle caps, Helical stairs on the cylindrical (cone & floating roof) tank, spherical tank, Strake, wind breaker on tall
column and chimney pipes/boiler & furnace flue gas pipes & flares, Screw pump vanes for pushing water and cement
& concrete slurry. Helical and spiral stairs in the house, offices and government buildings. Majority of the springs are in
the helical form. Helical gears.
Note : The above definition of Helix and Spiral are per Mathematics. However, many Civil Engineers still call Helical
Staircase as Spiral Staircase, if the stairs/step revolves around a central pole. If the steps are far away from the
center of the stairs, then they call them as helical or circular stair.
3525.564409
3D Geometry-Solid Shapes-Formulas for Length, Area, Volume
Chapter-B3 Circular-Helical-Spiral Curved Objects(stairs, strakes. . . ), Construction Details
By JGC Annamalai
(3). Straight up to the top Platform
(1). Straight up & Spiral Stair
(2). Straight up &
L & U-turn) Stair
Helical Stairs
23

24. Chapter-B3 Circular-Helical-Spiral Curved Objects(stairs, strakes. . . ), Construction Details
24

25. Chapter-B3 Circular-Helical-Spiral Curved Objects(stairs, strakes. . . ), Construction Details
Some of the Sphere Proportions & thumb rules :
Sphere inside Radius R
Sphere center located, above ground at 1.43R
Sphere Top Platform located, above ground at 2.444R
Straight stair, intermediate Platform located at 1.55R
Helical stair center, offset from sphere center 0.073R
Straight stair, located, off from sphere surface 700mm
Helical Stair outer Stringer (inner) radius 0.47R
Helical stair included angle 90+40=130°
Helical middle support @ 130/2=65°
Helical & Spiral Standard Stairs : Definitions : (BS-5395)
Spiral Stair : a stair describing a helix around a central column
Helical Stair : a stair describing a helix around a central void
Clear Width : the unobstructed walking area throughout the stair’s rise (760mm width, between string on Sph. Tank)
Outside Diameter : the diameter of the outer edge of the handrail, strings or treads, whichever is the greater
Nosing : the front edge of a tread
Riser : the part closing the front face of the step
Tread : the horizontal part or upper surface of the step
2r + t = 620 to 640 mm (25.5")
BS5395, <480(2r+g)<800
Stair Radius, Sample calculation :
Point on the helix, can be identified by (circular angle)
We will use polar co-ordinates, for easy understanding.
Hs. Height or rise of spiral stair step is h, (200mm).
Number of steps = Hs/h
L, helical curve length can be found.
For full height, H=14954mm (for 360°) Hs=0.0.3611 times H
φ=360*0.3611=130° N= 5400/200 =27 steps
h= φ=130°(2.27 rad) a= 1753mm b= 2089mm
From Dwg, Outer Tread, 232mm
for 27 steps, C=27*232 =6264
(for smaller angles <6°,sine angle, tangent angle and radians are will be same)
(eg for 5°, sin5=0.0872, tan5=0.0875, rad for 5°(Deg*3.1416/180) =0.0872)
Ro=Stair, outside radius, Ri=Stair, inside radius
C=2πRo(φ/360)=6264
Ro=C*360/(2πφ)=6264*360/(2*3.1416*130)
=2761mm
Ri=Ro-stair width
Clear Headroom : the distance measured vertically from the pitch lineof a stair or from a floor or landing to any
obstruction overhead
Going : the chord length on plan between two points on consecutive tread nosings at
the same radius from the geometric centre of the stair (230 to 250 mm on Spherical
Tank)
Rise : the vertical distance between two consecutive steps (200 mm on Spherical Tank)
Pitch Line : a line drawn from the floor or landing below a stair to connect
points on consecutive tread nosings at thesame radius from the geometric
centre of the stair
5400mm,
The most commonly used formula to calculate stairs dimensions is attributed
to the architect François Blondel, dating back to 1675. The famous formula
is based on the fact that the effort made to lift the foot vertically is equal to
twice the effort taken to move it horizontally. He specified that twice the riser
height plus the tread depth equals the step length:
where r is the value of the riser and
t & g are the tread / going.
(subtract excess width, if the steps
have treads / width with overlap)
25