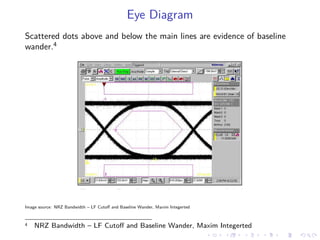
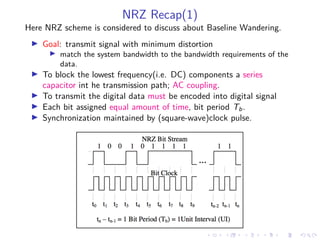
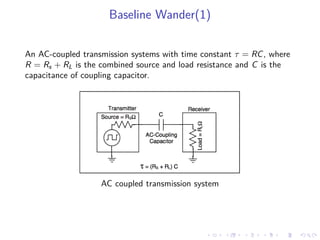
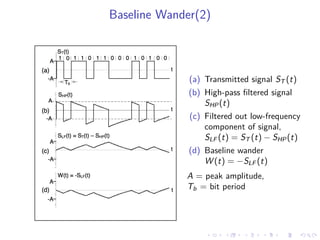
The document discusses baseline wandering in digital transmission, particularly in non-return-to-zero (NRZ) encoding, and its impact on bit error rates. It explores the mathematical explanations, observations, and effects of baseline wander, emphasizing how cumulative bit difference (CBD) and low-frequency (LF) cutoff influence the phenomenon. The document concludes that managing baseline wander involves ensuring an equal number of transmitted zeros and ones, alongside coding techniques to mitigate its effects.

1. Baseline Wandering
Digital Transmission: NRZ
CMS-A-CC-4-8
Lockdown Talk Series: DCNIT-LDTalks-4
Arunabha Saha
Department of Computer Science, Vidyasagar College
University of Calcutta
May 2020

2. Outline
Preliminaries : Bit Rate vs Signal Rate
Preliminaries: SNR vs E/BNR
Baseline Wandering Problem
Mathematical Explanation
Observations & Effects of Baseline Wander
Conclusions

3. Bit Rate vs Signal Rate
Bit rate: The number of bits transmitted per unit time.
Data rate: Rb = 1
Tb
; where Tb ≡ bit period.
Communication systems uses symbols, e.g binary - 0 or 1
Symbol rate: Rsym = 1
Ts
; where Ts ≡ symbol’s period. Also known
as Baud rate.
Relation between Rb and Rsym
Rb = Rsym × log2(L) = Rsym × n
where L = 2n
= # of levels(for n bits per symbol)

4. SNR vs E/BNR(1)
SNR measured in decibel(dB): SNRdB = 10.log10(SNR)
Another useful metric energy per bit to noise ratio(E/BNR), Eb
N0
Rb = bit rate (in bits per second)
S = total signal power (watts)
Eb = energy per bit (in joules/bit)
N = total noise power (over entire bandwidth B in Hz)
N0 = noise spectral density
N = N0.B, Then by definition,
S
Rb
= Eb ⇒
Eb
N
=
S
Rb.N
⇒
S
N
=
Rb.Eb
N0.B
SNR = Rb.Eb
N0.B
With increasing Rb increase the SNR, i.e. SNR ∝ Rb; Also it increases
noise which reduce the SNR.

5. SNR vs E/BNR(2)
In digital communications systems, the Eb/N0 ratio can be thought of as
a normalized signal-to-noise ratio.
We can roughly equate signal power to energy per bit by
Eb = Psignal .Ts
Eb
N0
generally used to establish the bit error rate(BER) for modulation
techniques.

6. NRZ Recap(1)
Here NRZ scheme is considered to discuss about Baseline Wandering.
Goal: transmit signal with minimum distortion
match the system bandwidth to the bandwidth requirements of the
data.
To block the lowest frequency(i.e. DC) components a series
capacitor int he transmission path; AC coupling.
To transmit the digital data must be encoded into digital signal
Each bit assigned equal amount of time, bit period Tb.
Synchronization maintained by (square-wave)clock pulse.

7. NRZ: PSD(2)
The power spectral density(PSD) of NRZ scheme mathematically given
by
Su(f ) = αTbSinc2
(Tbf ) (1)
where Sinc(x) = Sin(πx)
πx , α is proportionality constant and f is frequency
in Hz.
power spectrum of random NRZ data

8. NRZ: Low-Frequency(LF) Cutoff(3)
The NRZ power spectrum got modified on attenuating the LF
components. The normalized frequency, Tbfc represents the half-power
(3 dB) frequency termed as LF cutoff.
Loss of the low-frequency
portion of the signal power
will reduce the SNR and
thus degrade the BER.
By removing the LF
components the BER will
be reduced, known as
baseline wandering.

9. Baseline Wander(1)
An AC-coupled transmission systems with time constant τ = RC, where
R = Rs + RL is the combined source and load resistance and C is the
capacitance of coupling capacitor.
AC coupled transmission system

10. Baseline Wander(2)
(a) Transmitted signal ST (t)
(b) High-pass filtered signal
SHP(t)
(c) Filtered out low-frequency
component of signal,
SLF (t) = ST (t) − SHP(t)
(d) Baseline wander
W (t) = −SLF (t)
A = peak amplitude,
Tb = bit period

11. Baseline Wander: Mathematical explanation(3)
The NRZ bit-stream in fig. (a) mathematically a unit step function
u(t) =
0, t < 0
1, t ≥ 0
(2)
Now express ST (t) in terms of u(t)
ST (t) = Au(t) − 2Au(t − Tb) + 2Au(t − 2Tb) − 2Au(t − 4Tb)
+ 2Au(t − 5Tb) − .... (3)

12. Baseline Wander: Mathematical explanation(4)
The step response of a single-time-constant high-pass network1
is equal
to e−t/τ
, using this the expression for high-pass filtered signal
SHP(t) = Au(t)e− t
τ − 2Au(t − Tb)e−
(t−Tb)
τ + 2Au(t − 2Tb)e−
(t−2Tb)
τ
− 2Au(t − 4Tb)e−
(t−4Tb)
τ + 2Au(t − 5Tb)e−
(t−5Tb)
τ − .... (4)
the eqn(4) shown in the fig(b).
SLF can be obtained from the difference between the original(ST (t)) and
the high-pass filtered signal(SHP(t)), shown in fig(c)
SLF = ST (t) − SHP(t)
= Au(t)(1 − e− t
τ ) − 2Au(t − Tb)(1 − e−
(t−Tb)
τ )
+ 2Au(t − 2Tb)(1 − e−
(t−2Tb)
τ ).... (5)
1 Miroelectronics Circuits, Sedra, A.S.; Smith, K.C.(1982), pp.60-61

13. Baseline Wander: Mathematical explanation(5)
Now we can see from fig(b), the average value(i.e. the midpoint) of the
high-pass signal shown in fig.(b) changes due to reduction of LF
components. This variation in the average midpoint is known as baseline
wander.
W (t) = −SLF (t)
= −Au(t)(1 − e− t
τ ) + 2Au(t − Tb)(1 − e−
(t−Tb)
τ )
− 2Au(t − 2Tb)(1 − e−
(t−2Tb)
τ ).... (6)
eqn.(6) represented by fig.(d).

14. Observations: CBD definition(1)
Define Cumulative bit difference(CBD), difference between the number of
transmitted zeros and the number of transmitted ones2
,
CBD[n] = N0[n] − N1[n] (7)
where CBD[n] = cumulative bit difference at the n-th bit of the pattern
N0 = cumulative number of 0s in the pattern up to the n-th bit
N1 = cumulative number of 1s in the pattern up to the n-th bit
2 NRZ Bandwidth – LF Cutoff and Baseline Wander, Maxim Integerted

15. Observations
Magnitude of baseline wander in NRZ determined by CBD[n] and LF
cutoff.
Baseline wander changes fastest when there are consecutive identical
digits(CID), and this also changes the CBD too.
Apart from CIDs, and imbalance in number of 0s and 1s create
wandering.
The baseline wander depend on the CBD only when the CBD is
computed over a number of bit periods that constitute a small
fraction of one time constant.

16. Linear approximation(1)
– Change in the baseline wander over the time of a single bit or CIDs is
exponential function; non-linear in nature.
– The overall change in baseline wander depends upon the ordering of
the bits.

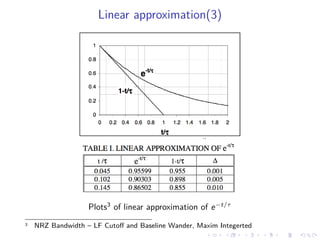
17. Linear approximation(2)
– Assumption: rate of change of baseline wander is constant(i.e. linear).
– For linear baseline wander, the offset will adds up linearly irrespective of
the bit pattern.
– Then approximate baseline wander can be a function of local CBD.
using the linear approximation, eqn.(6) reduced to,
W (t) = −Au(t) 1 −
t
Tb
+ 2Au(t − Tb) 1 −
t − Tb
τ
(8)
– Taking summation over entire bit sequence in eqn.(8)
W (t) = CBD[n] ×
Tb
τ
(9)

18. Linear approximation(3)
Plots3
of linear approximation of e−t/τ
3 NRZ Bandwidth – LF Cutoff and Baseline Wander, Maxim Integerted

19. Eye Diagram
Scattered dots above and below the main lines are evidence of baseline
wander.4
Image source: NRZ Bandwidth – LF Cutoff and Baseline Wander, Maxim Integerted
4 NRZ Bandwidth – LF Cutoff and Baseline Wander, Maxim Integerted

20. Wrap-up with Conclusions
Q. What is Baseline wander? reason? result?
– It is a slow variation the the average of the signal waveform.
Caused by attenuation and LF components of the signal.
Increase jitter and reduce BER.
Q. How can be controlled?
– Ensuring nearly equal number of 0s and 1s will manage to keep small
LF cutoff.
Using some smart coding techniques, e.g. data scrambling and 8b/10b
encoding to control CBD and limit LF contents.

21. Thank You
Image source: Google Images
all materials and codes are copyright protected under GNU GPL and Creative Commons(cc) license. Anyone can share or redistribute for
non-commercial purpose only. Usage of any lecture materials or(and) codes by any individual or institution for commercial benefits or
advancement without permission is strictly prohibited.