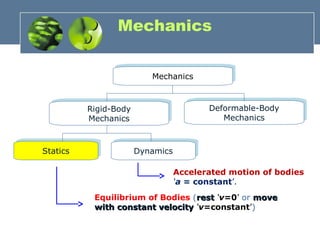
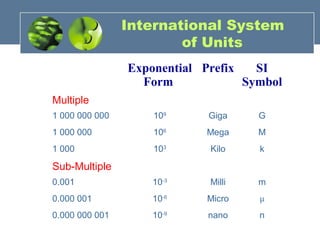
The document introduces the principles of engineering mechanics, focusing on statics, which involves the study of forces, moments, and equilibrium. It emphasizes learning the specific terminology and methods unique to engineering mechanics, akin to learning a new language, and outlines the fundamental concepts, units of measurement, and procedures for solving problems. The chapter also covers Newton's laws of motion, the significance of significant figures in calculations, and a systematic approach to problem analysis.

1. Engineering
Mechanics: Statics
Chapter 1: General
Principles

2. • Statics will build upon what you were
supposed to learn in your basic
physics and mathematics courses.
• We will talk about forces – vector
forces – about moments and torques,
reactions and the requirements of
static equilibrium of a particle or a
rigid body.
WHY Statics?

3. • You have seen a good bit of the basic
stuff of this course before, but we will
not assume you know the way to talk
about, or work with, these concepts,
principles, and methods so
fundamental to our subject.
• So we will recast the basics in our own
language, the language of engineering
mechanics.
WHY Statics?

4. • Think of this course as a language text; of
yourself as a language student beginning
the study of Engineering Mechanics
(Statics).
• You must learn the language if you aspire
to be an engineer.
• But this is a difficult language to learn,
unlike any other foreign language you have
learned.
WHY Statics?

5. • It is difficult because, on the surface, it
appears to be a language you already know.
But you will have to be on guard, careful,
not to presume the word you have heard
before bears the same meaning.
Words and phrases you have already used
now take on a more special and, in most
cases, narrower meaning; a couple of forces
is more than just two forces.
WHY Statics?

6. • The best way to learn a new language is
to use it – speak it, read it, listen to it on
audio tapes, watch it on television; better
yet, go to the land where it is the language
in use and use it to buy a loaf of bread, get
a hotel room for the night, ask to find the
nearest post office.
WHY Statics?

7. • So too in statics, we insist you begin to
use the language. Doing problems and
exercises, taking quizzes and the final, is
using the language.
• Statics course contains exercises
explained, as well as exercises for you to
tackle such as homeworks...
WHY Statics?

8. Chapter Outline
• Mechanics (an introduction)
• Fundamental Concepts (Newton’s Laws
of Motion)
• The International System of Units
(principles for applying the SI)
• Units of Measurement
• Numerical Calculations (procedures for
performing numerical calculations)
• General Procedure for Analysis (solving
problems)

9. Mechanics
• Mechanics can be divided into 2 branches:
1- Rigid-body Mechanics
2- Deformable-body Mechanics
- Solid bodies
- Fluids (liquids and gases
• Rigid-body Mechanics deals with
- Statics
- Dynamics

10. MechanicsMechanics
Rigid-Body
Mechanics
Rigid-Body
Mechanics
Deformable-Body
Mechanics
Deformable-Body
Mechanics
StaticsStatics DynamicsDynamics
Accelerated motion of bodies
‘a = constant’.
Equilibrium of Bodies (restrest ‘v=0’ or movemove
with constant velocitywith constant velocity ‘v=constant’)
Mechanics

11. Mechanics
• Statics – Equilibrium of bodies
At rest
Move with constant velocity
• Dynamics – Non-equilibrium of bodies
Accelerated / Deccelerated motion of
bodies

12. What may happen if statics is
not applied properly

13. Force
– “push” or “pull” exerted by one body on another
– Occur due to direct contact between bodies
Eg: Person pushing against the wall
– Occur through a distance without direct contact
Eg: Gravitational, electrical and magnetic forces
Fundamentals Concepts

14. Fundamentals Concepts
• Particles
– Consider mass but neglect size
Eg: Size of Earth insignificant compared to its
size of orbit
• Rigid Body
– Combination of large number of particles
– Neglect material properties
Eg: Deformations in structures, machines and
mechanism

15. Fundamentals Concepts
• Concentrated Force
– Effect of loading, assumed to act at a point on
a body
– Represented by a concentrated force,
provided loading area is small compared to
overall size
Eg: Contact force between
wheel and ground

16. Fundamentals Concepts
Newton’s Three Laws of Motion
• First Law
“A particle originally at rest, or moving in a
straight line with constant velocity, will remain in
this state provided that the particle is not
subjected to an unbalanced
force”
First Law:
ΣF = 0

17. Fundamentals Concepts
Newton’s Three Laws of Motion
• Second Law
“A particle acted upon by an unbalanced force F
experiences an acceleration ‘a’ that has the
same direction as the force and a magnitude that
is directly proportional to the
force”
Second Law:
ΣF =

18. Fundamentals Concepts
Newton’s Three Laws of Motion
• Third Law
“The mutual forces of action and reaction
between two particles are equal and opposite
and collinear”
Third law:
Faction= Freaction

19. Fundamentals Concepts
WEIGHT
• m is the mass (kg)
• g is the acceleration due to gravity
(m/s2
)
• Most engineering calculations, g
at sea level and at a latitude of 45°
is enough. g=9.81 m/s2
W mg=

20. Fundamentals Concepts
• At the standard location,
g = 9.806 65 m/s2
• For calculations, we use
g = 9.81 m/s2
• Thus,
W = mg (g = 9.81m/s2
)
• Hence, a body of mass 1 kg has a weight
of 9.81 N, a 2 kg body weighs 19.62 N

21. Units of Measurement
Basic Quantities
• Length
– Locate position and describe size of physical
system
– Define distance and geometric properties of a
body

22. Units of Measurement
Basic Quantities
• Mass
– Comparison of action of one body against
another
– Measure of resistance of matter to a change in
velocity

23. Basic Quantities
• Time
– Period between two succession of events
Units of Measurement

24. Units of Measurement
SI Units
• Système International d’Unités
• F = ma is maintained only if
– Three of the units, called basic units, are
arbitrarily defined
– Fourth unit is derived from the equation
• SI units specifies:
 length in meters (m),
 time in seconds (s) and
 mass in kilograms (kg)
• Unit of force, called Newton (N) is derived from
F = ma

25. Units of Measurement






2
.
s
mkg
Name Length Time Mass Force
International
Systems of
Units (SI)
Meter
(m)
Second
(s)
Kilogram
(kg)
Newton
(N)

26. The International
System of Units
Prefixes
• For a very large or very small numerical
quantity, the units can be modified by
using a prefix
• Each represent a multiple or sub-multiple
of a unit
Eg: 4 000 000 N = 4 000 kN (kilo-Newton)
= 4 MN (Mega- Newton)
0.005 m = 5 mm (milli-meter)

27. International System
of Units
Exponential
Form
Prefix SI
Symbol
Multiple
1 000 000 000 109
Giga G
1 000 000 106
Mega M
1 000 103
Kilo k
Sub-Multiple
0.001 10-3
Milli m
0.000 001 10-6
Micro μ
0.000 000 001 10-9
nano n

28. International System
of Units
Rules for Use
• Never write a symbol with a plural “s”.
Easily confused with second (s)
• Symbols are always written in lowercase
letters, except the 2 largest prefixes, mega
(M) and giga (G)
• Symbols named after an individual are
capitalized Eg: Newton (N)

29. International System
of Units
Rules for Use
• Quantities defined by several units which
are multiples, are separated by a dot
Eg: N = kg.m/s2
= kg.m.s-2
• The exponential power represented for a
unit having a prefix refer to both the unit
and its prefix
Eg: μN2
= (μN)2
= μN. μN

30. • If a derived unit is obtained by dividing a basic unit
to an other basic unit, the prefix should always be
used for the unit at the numerator and never for the
unit at the denominator.
• Ex: If under 100 N load, a spring elongates 20 mm,
the elongation constant ‘k’ of the spring is:
�=(100 N)/(20 mm)=(100 N)/(0.02 m) = 5000 N/m
or = 5 kN/m
Never k = 5 N/mm
International System
of Units

31. International System
of Units
Rules for Use
• Physical constants with several digits on
either side should be written with a space
between 3 digits rather than a comma (,)
Eg: 73 569.213 427

32. Numerical
Calculations
Significant Figures
- The accuracy of a number is specified by the
number of significant figures it contains.
- A significant figure is any digit including even
zero. The location of the decimal point of a
number is not important
Eg: 5 604 and 34.52 both have four significant
numbers

33. Numerical
Calculations
Significant Figures
- When numbers begin or end with zero, we make
use of prefixes to clarify the number of significant
figures
Eg: 400 → as 1 significant figure would be 0.4 (103
)
or 4 (102
)
2 500 → as 3 significant figures would be 2.50 (103
)

34. Numerical
Calculations
Rounding Off Numbers
For numerical calculations, the accuracy
obtained from the solution of a problem
would never be better than the accuracy of
the problem data!
Often handheld calculators or computers
involve more figures in the answer than the
number of significant figures in the data.

35. Numerical
Calculations
Rounding Off Numbers
Calculated results should always be
“rounded off” to an appropriate number of
significant figures.

36. Numerical
Calculations
To ensure the accuracy of the final results,
always give your answers 3 digits after the
decimal point.
Eg: 45.703
101.007
1 398.400

37. Numerical
Calculations
For plane angles used in trigonometry, in this
course, please give your answers in 4 digits
after the decimal point both for the angles and
their trigonometric equivalencies.
Eg: Sin 35.0000˚
= 0.5736
Cos 45.0380˚
= 0.7066
Tan-1
1.3459 = 53.3878˚

38. General Procedure
for Analysis
• Most efficient way of learning is to
solve problems:
• To be successful at this, it is important to present
the work in a logical and orderly way as
suggested:
1) Read the problem carefully and try to correlate
actual physical situation with theory;
2) Draw any necessary diagrams and tabulate
the problem data;

39. General Procedure
for Analysis
3) Apply relevant principles, generally in
mathematical forms;
4) Solve the necessary equations, algebraically
as far as practical, making sure that they are
dimensionally homogenous, using a consistent
set of units and complete the solution
numerically;

40. General Procedure
for Analysis
5) Report the answer with no more significance
figures than accuracy of the given data;
6) Study the answer with technical judgment and
common sense to determine whether or not it
seems reasonable.