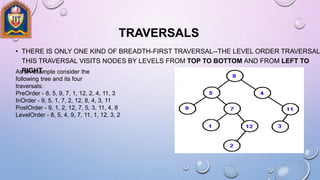
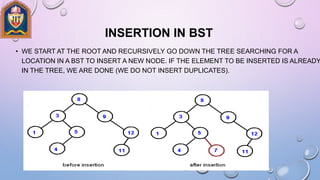
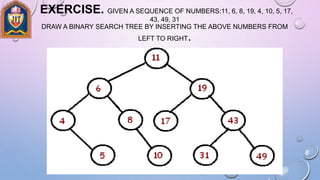
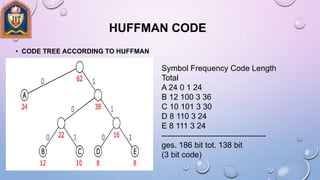
The document discusses different tree data structures and traversal algorithms. It begins by defining tree terminology like nodes, leaves, height, depth. It then explains binary trees in more detail and their properties like full/complete binary trees. Different tree traversal algorithms are covered like preorder, inorder, postorder traversals. Binary search trees and their insertion process are described. Extended binary trees, threaded binary trees, and Huffman coding trees are also summarized. Examples and diagrams are provided to illustrate the various tree concepts and algorithms.

1. DATA STRUCTURES USING C
(NCS-301)
SUBMITTED BY : MRS. SWETA SINGH
ASSISTANT PROFESSOR(CSE)
JIT BARABANKI(UP.)

2. UNIT – 3
TREES

3. TREES TERMINOLOGY
A NODE IS A STRUCTURE WHICH MAY CONTAIN A VALUE, A CONDITION, OR REPRESENT A
SEPARATE DATA STRUCTURE (WHICH COULD BE A TREE OF ITS OWN). EACH NODE IN A TREE HAS
ZERO OR MORE CHILD NODES, WHICH ARE BELOW IT IN THE TREE (BY CONVENTION, TREES
GROW DOWN, NOT UP AS THEY DO IN NATURE).
• A NODE THAT HAS A CHILD IS CALLED THE CHILD'S PARENT NODE (OR ANCESTOR NODE, OR
SUPERIOR). A NODE HAS AT MOST ONE PARENT.
• NODES THAT DO NOT HAVE ANY CHILDREN ARE CALLED LEAF NODES. THEY ARE ALSO
REFERRED TO AS TERMINAL NODES.
• THE HEIGHT OF A NODE IS THE LENGTH OF THE LONGEST DOWNWARD PATH TO A LEAF FROM
THAT NODE.
• THE HEIGHT OF THE ROOT IS THE HEIGHT OF THE TREE.
• THE DEPTH OF A NODE IS THE LENGTH OF THE PATH TO ITS ROOT (I.E., ITS ROOT PATH).

4. BINARY TREE
• THE BINARY TREE IS A FUNDAMENTAL DATA STRUCTURE USED IN
COMPUTER SCIENCE. THE BINARY TREE IS A USEFUL DATA STRUCTURE
FOR RAPIDLY STORING SORTED DATA AND RAPIDLY RETRIEVING
STORED DATA.
• A BINARY TREE IS COMPOSED OF PARENT NODES, OR LEAVES, EACH OF
WHICH STORES DATA AND ALSO LINKS TO UP TO TWO OTHER CHILD
NODES (LEAVES) WHICH CAN BE VISUALIZED SPATIALLY AS BELOW THE
FIR
• THE DEPTH OF A NODE IS THE NUMBER OF EDGES FROM THE ROOT TO
THE NODE.
• THE HEIGHT OF A NODE IS THE NUMBER OF EDGES FROM THE NODE TO
THE DEEPEST LEAF.
• THE HEIGHT OF A TREE IS A HEIGHT OF THE ROOT.
• A FULL BINARY TREE.IS A BINARY TREE IN WHICH EACH NODE HAS
EXACTLY ZERO OR TWO CHILDREN.
• A COMPLETE BINARY TREE IS A BINARY TREE, WHICH IS COMPLETELY
FILLED, WITH THE POSSIBLE EXCEPTION OF THE BOTTOM LEVEL, WHICH
IS FILLED FROM LEFT TO RIGHT.ST NODE WITH ONE PLACED TO THE

5. BINARY TREE
A complete binary tree is very special tree, it provides the best
possible ratio between the number of nodes and the height.
The height h of a complete binary tree with N nodes is at most O(log N).
n = 1 + 2 + 4 + ... + 2h-1 + 2h = 2h+1 - 1
Advantages of trees
Trees are so useful and frequently used, because they have some very serious advantages:
Trees reflect structural relationships in the data
Trees are used to represent hierarchies
Trees provide an efficient insertion and searching
Trees are very flexible data, allowing to move sub trees around with minimum effort

6. TRAVERSALS
• A TRAVERSAL IS A PROCESS THAT VISITS ALL THE NODES IN THE TREE. SINCE A TREE IS A
NONLINEAR DATA STRUCTURE, THERE IS NO UNIQUE TRAVERSAL. WE WILL CONSIDER
SEVERAL TRAVERSAL ALGORITHMS WITH WE GROUP IN THE FOLLOWING TWO KINDS
• DEPTH-FIRST TRAVERSAL
• BREADTH-FIRST TRAVERSAL
• THERE ARE THREE DIFFERENT TYPES OF DEPTH-FIRST TRAVERSALS,
• PREORDER TRAVERSAL - VISIT THE PARENT FIRST AND THEN LEFT AND RIGHT CHILDREN;
• INORDER TRAVERSAL - VISIT THE LEFT CHILD, THEN THE PARENT AND THE RIGHT CHILD;
• POSTORDER TRAVERSAL - VISIT LEFT CHILD, THEN THE RIGHT CHILD AND THEN THE
PARENT;

7. TRAVERSALS
• THERE IS ONLY ONE KIND OF BREADTH-FIRST TRAVERSAL--THE LEVEL ORDER TRAVERSAL
THIS TRAVERSAL VISITS NODES BY LEVELS FROM TOP TO BOTTOM AND FROM LEFT TO
RIGHT.As an example consider the
following tree and its four
traversals:
PreOrder - 8, 5, 9, 7, 1, 12, 2, 4, 11, 3
InOrder - 9, 5, 1, 7, 2, 12, 8, 4, 3, 11
PostOrder - 9, 1, 2, 12, 7, 5, 3, 11, 4, 8
LevelOrder - 8, 5, 4, 9, 7, 11, 1, 12, 3, 2

8. BINARY SEARCH TREES
• A BST IS A BINARY TREE WHERE NODES ARE ORDERED IN THE FOLLOWING WAY:
• EACH NODE CONTAINS ONE KEY (ALSO KNOWN AS DATA)
• THE KEYS IN THE LEFT SUBTREE ARE LESS THEN THE KEY IN ITS PARENT NODE, IN SHORT
L < P;
• THE KEYS IN THE RIGHT SUBTREE ARE GREATER THE KEY IN ITS PARENT NODE, IN SHORT
P < R;
• DUPLICATE KEYS ARE NOT ALLOWED.In the following tree all nodes in the left subtree of 10
have keys < 10 while all nodes in the right subtree >
10. Because both the left and right subtrees of a BST
are again search trees; the above definition is
recursively applied to all internal nodes:

9. INSERTION IN BST
• WE START AT THE ROOT AND RECURSIVELY GO DOWN THE TREE SEARCHING FOR A
LOCATION IN A BST TO INSERT A NEW NODE. IF THE ELEMENT TO BE INSERTED IS ALREADY
IN THE TREE, WE ARE DONE (WE DO NOT INSERT DUPLICATES).

10. EXERCISE. GIVEN A SEQUENCE OF NUMBERS:11, 6, 8, 19, 4, 10, 5, 17,
43, 49, 31
DRAW A BINARY SEARCH TREE BY INSERTING THE ABOVE NUMBERS FROM
LEFT TO RIGHT.

11. EXTENDED BINARY TREE: 2-TREES
• A BINARY TREE IS SAID TO BE A 2-TREE OR AN EXTENDED BINARY TREE IF EACH NODE N
HAS EITHER 0 OR 2 CHILDREN.
• IN SUCH A CASE, NODES WITH 2 CHILDREN ARE CALLED INTERNAL NODES, AND NODES
WITH 0 CHILD ARE CALLED EXTERNAL NODES.
• THE EXTERNAL AND INTERNAL NODES ARE DISTINGUISHED DIAGRAMMATICALLY BY
USING CIRCLES FOR INTERNAL NODES AND SQUARES FOR EXTERNAL NODES

12. THREADED BINARY TREE
• A THREADED BINARY TREE DEFINED AS FOLLOWS:
• "A BINARY TREE IS THREADED BY MAKING ALL RIGHT CHILD POINTERS THAT WOULD NORMALLY BE NULL
POINT TO THE INORDER SUCCESSOR OF THE NODE (IF IT EXISTS) , AND ALL LEFT CHILD POINTERS THAT
WOULD NORMALLY BE NULL POINT TO THE INORDER PREDECESSOR OF THE NODE.”
• A THREADED BINARY TREE MAKES IT POSSIBLE TO TRAVERSE THE VALUES IN THE BINARY TREE VIA A
LINEAR
• TRAVERSAL THAT IS MORE RAPID THAN A RECURSIVE IN-ORDER TRAVERSAL. IT IS ALSO POSSIBLE TO
DISCOVER THE PARENT OF A NODE FROM A THREADED BINARY TREE, WITHOUT EXPLICIT USE OF PARENT
POINTERS OR A STACK, ALBE IT SLOWLY.
• TYPES OF THREADED BINARY TREES
• 1. SINGLE THREADED: EACH NODE IS THREADED TOWARDS EITHER(RIGHT)' THE IN-ORDER
• PREDECESSOR OR' SUCCESSOR.
• 2. DOUBLE THREADED: EACH NODE IS THREADED TOWARDS BOTH(LEFT & RIGHT)' THE IN-ORDER
• PREDECESSOR AND' SUCCESSOR.

13. HUFFMAN CODE
• THE ALGORITHM AS DESCRIBED BY DAVID HUFFMAN ASSIGNS EVERY SYMBOL TO A
LEAF NODE OF A BINARY CODE TREE.
• THESE NODES ARE WEIGHTED BY THE NUMBER OF OCCURRENCES OF THE
CORRESPONDING SYMBOL CALLED FREQUENCY OR COST.
• THE TREE STRUCTURE RESULTS FROM COMBINING THE NODES STEP-BY-STEP UNTIL
ALL OF THEM ARE EMBEDDED IN A ROOT TREE.
• THE ALGORITHM ALWAYS COMBINES THE TWO NODES PROVIDING THE LOWEST
FREQUENCY IN A BOTTOM UP PROCEDURE.

14. HUFFMAN CODE
• EG: THE FOLLOWING EXAMPLE BASES ON A DATA SOURCE USING A SET OF FIVE DIFFERENT
SYMBOLS. THE
• SYMBOL'S FREQUENCIES ARE: SYMBOL FREQUENCY
• A 24
• B 12
• C 10
• D 8
• E 8
• ----> TOTAL 186 BIT (WITH 3 BIT PER CODE WORD)
• THE TWO RAREST SYMBOLS 'E' AND 'D' ARE CONNECTED FIRST, FOLLOWED BY 'C' AND 'D'. THE NEW
PARENT NODES
• HAVE THE FREQUENCY 16 AND 22 RESPECTIVELY AND ARE BROUGHT TOGETHER IN THE NEXT STEP.
THE RESULTING NODE

15. HUFFMAN CODE
• CODE TREE ACCORDING TO HUFFMAN
Symbol Frequency Code Length
Total
A 24 0 1 24
B 12 100 3 36
C 10 101 3 30
D 8 110 3 24
E 8 111 3 24
---------------------------------------
ges. 186 bit tot. 138 bit
(3 bit code)

16. THANK YOU