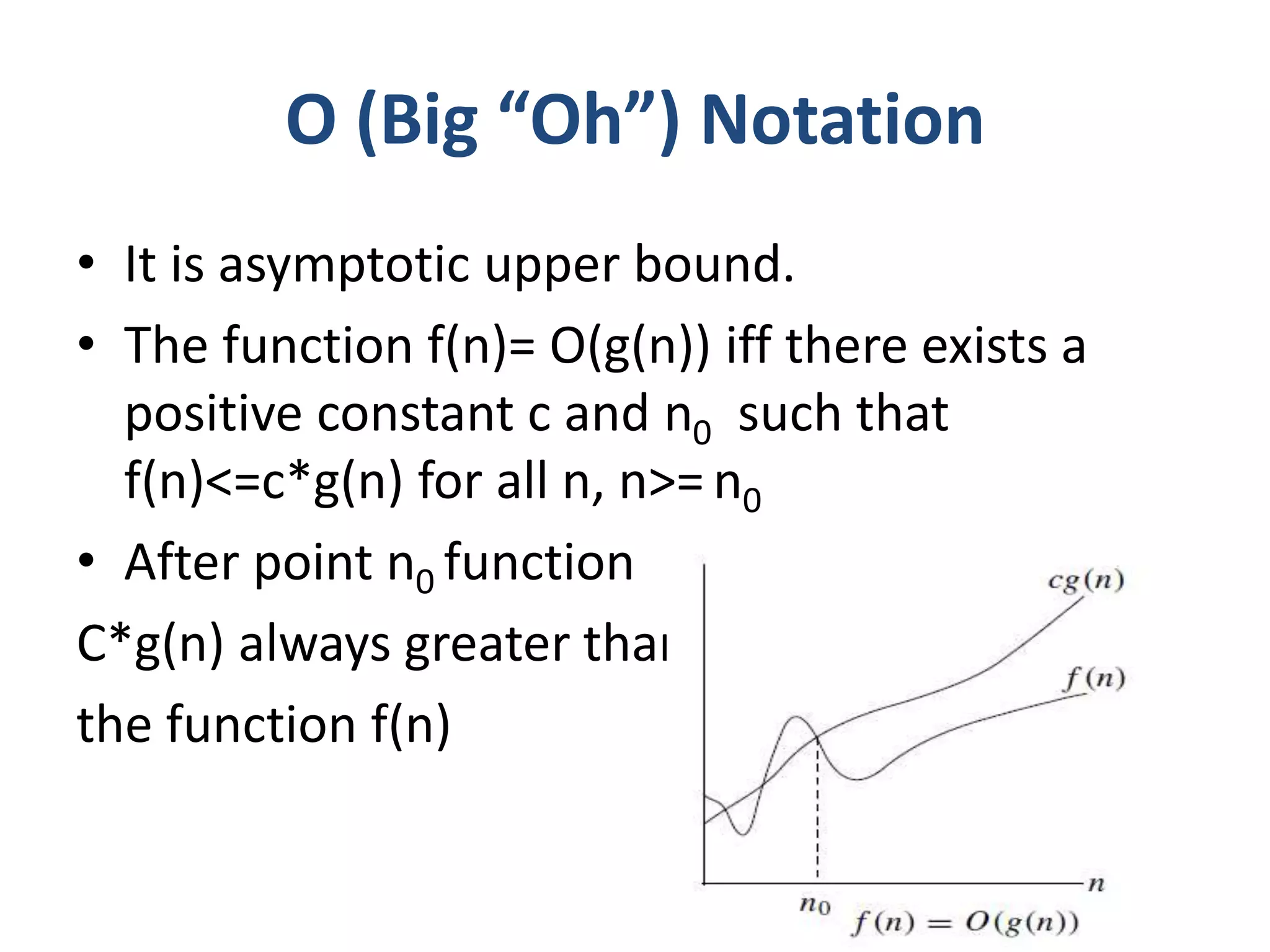
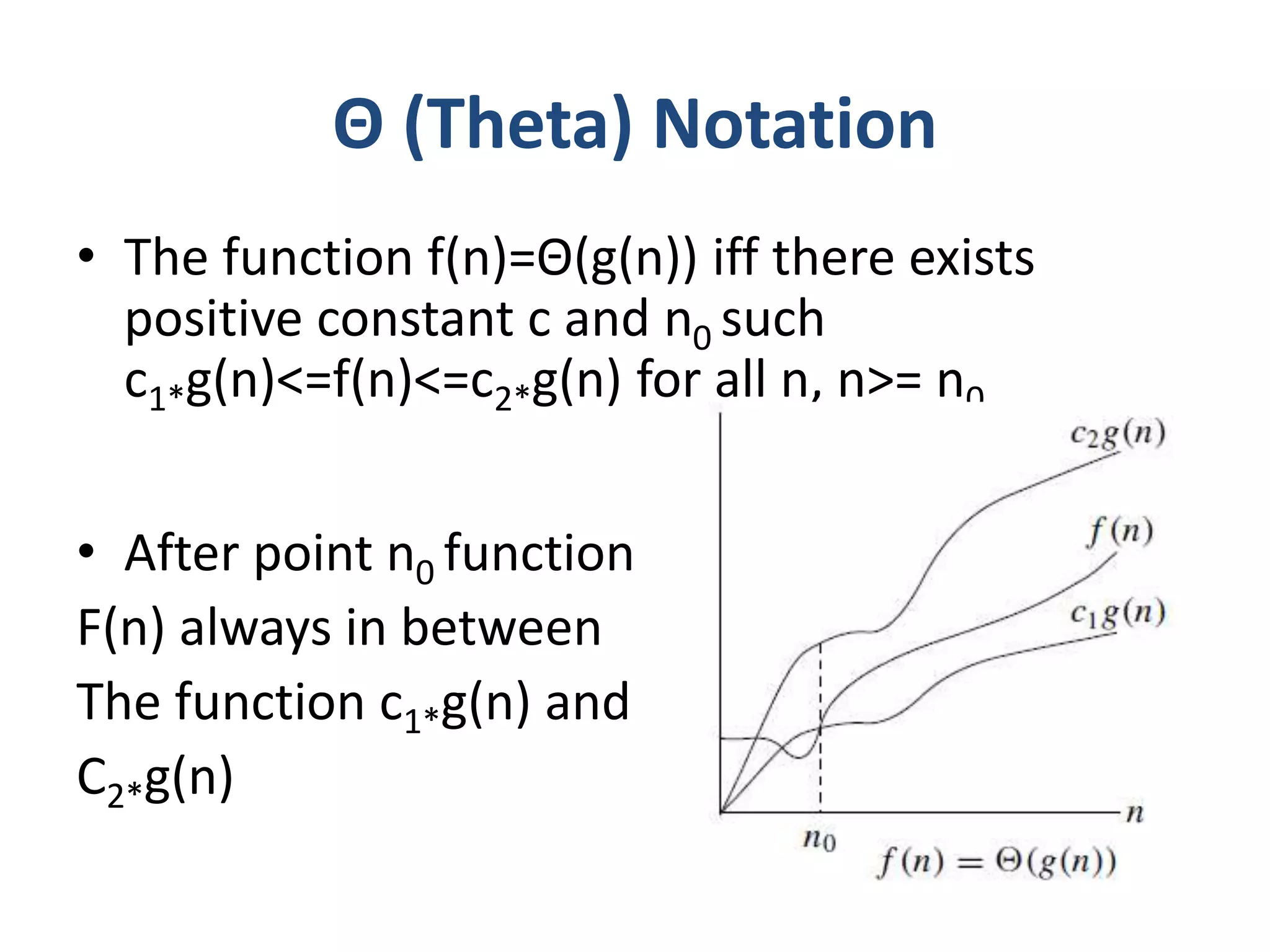
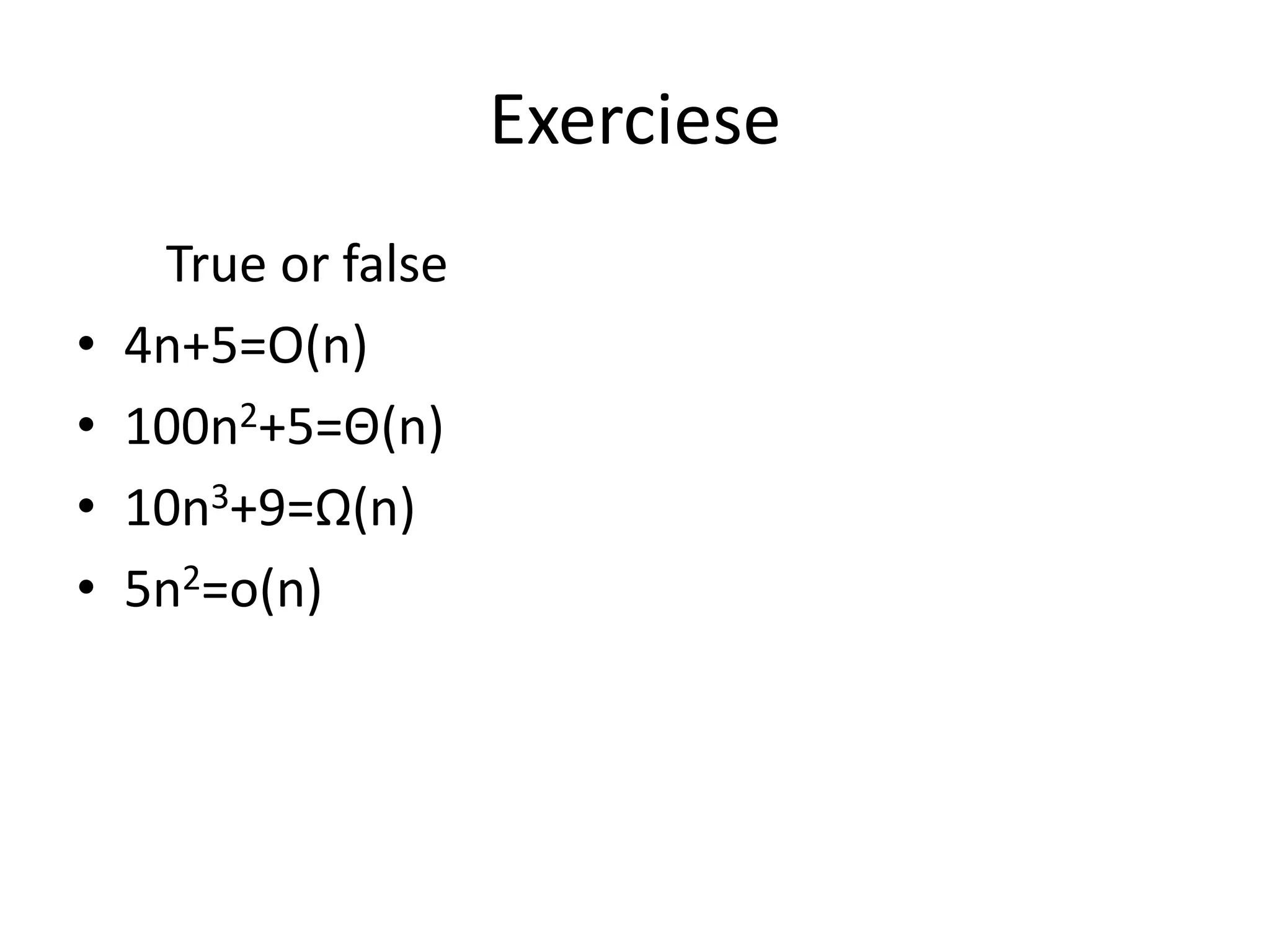Asymptotic notation describes the limiting behavior of algorithms as the problem size increases. There are three main types of asymptotic notation: Big-O (Ο) notation provides an asymptotic upper bound - a function f(n) is O(g(n)) if there exists a constant c such that f(n) is eventually less than or equal to c*g(n). Omega (Ω) notation provides an asymptotic lower bound - a function f(n) is Ω(g(n)) if there exists a constant c such that f(n) is eventually greater than or equal to c*g(n). Theta (Θ) notation provides both a lower and upper

1. Asymptotic Notation
Prepared by
Deepali A. Lokare

2. What is Asymptotic notation
• Asymptotic is a method of describing limiting
behavior.
• To find out the limiting behavior of any
problem.
• The type of behavior
– Worst case
– Best case
– Average case

3. Worst case
• Upper Limit
• To solve the problem require maximum time
and not above that.
• Example :-
• Travelling from Mumbai to Goa require 12
hours by travels. By own vehicle require 10
hours
• Worst case 12 hours not more than that.

4. Best Case
• Lower limit
• To solve the problem require minimum time
not less than that
• Example Travelling from Mumbai to Goa with
own vehicle require 10 hours. By travels 12
hours.
• Best case 10 hours not less than that.

5. Average Case
• In between upper limit and lower limit.
• To solve the problem need to find out time
require in between upper limit (Worst
case)and lower limit(Best case).

6. Ο (Big “Oh”) Notation
• It is asymptotic upper bound.
• The function f(n)= Ο(g(n)) iff there exists a
positive constant c and n0 such that
f(n)<=c*g(n) for all n, n>= n0
• After point n0 function
C*g(n) always greater than
the function f(n)

7. Ο (Big “Oh”) Notation
• Example
• 3n+2= Ο (n) as 3n+2 is function f(n) we need to find out
c*g(n) function
• Answer is 3n+2<=4*n
• C*g(n) is 4*n
• i.e function greater than 3n+2.
• 3n+2<=4n
• Put n=1; 3(1)+2 <=4(1) => 5 <=4 ….?
put n=2; 3(2)+2<=4(2) => 5<=8
put n=3; 3(3)+2<=4(3) => 8<=12 value of n0=2
• After n0 4n is always greater

8. Ω (omega) notation
• It is asymptotic lower bound
• The function f(n)= Ω(g(n)) iff there exists
positive constant c and no such that
f(n)>=c*g(n) for all n, n>=no
• After point n0 function
C*g(n) always less than the
function f(n)

9. Ω (omega) notation
• Example
• 100n+2=Ω(n)
• 100n+2>=100n
• put n=1; 100(1)+2 100(1)
Ans:- 102 101
put n=2; 100(2)+2 100(2)
Ans:-202 200 n0=1

10. Θ (Theta) Notation
• The function f(n)=Θ(g(n)) iff there exists
positive constant c and n0 such
c1*g(n)<=f(n)<=c2*g(n) for all n, n>= n0 .
• After point n0 function
F(n) always in between
The function c1*g(n) and
C2*g(n)

11. Θ (Theta) Notation
• Example
• 3n<=3n+2<=4n
• 3n is function c1g(n)
• 3n+2 is function f(n)
• 4n is the function c2g(n)

12. Exerciese
True or false
• 4n+5=O(n)
• 100n2+5=Θ(n)
• 10n3+9=Ω(n)
• 5n2=o(n)