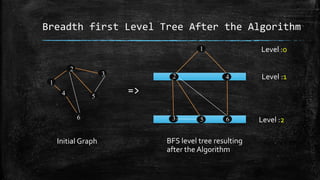
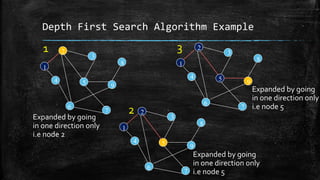
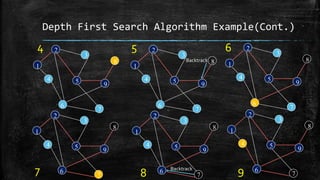
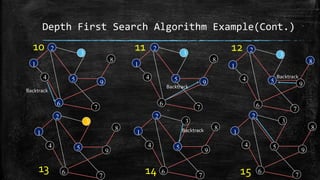
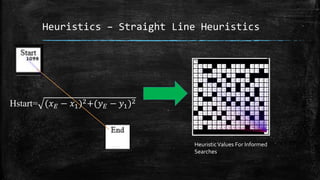
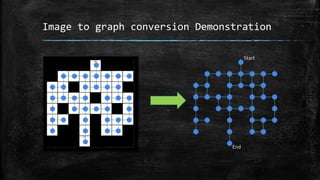
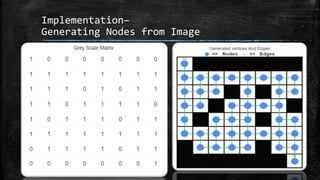
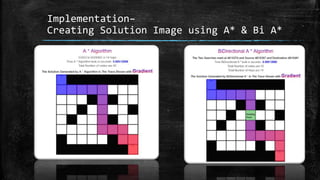
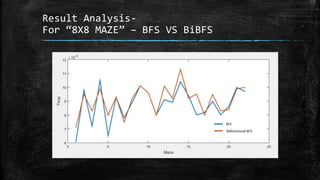
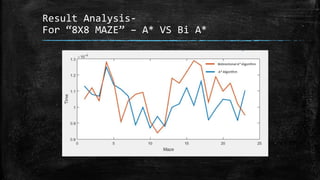
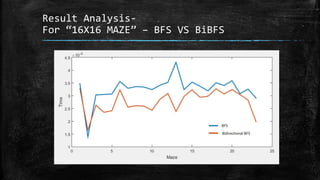
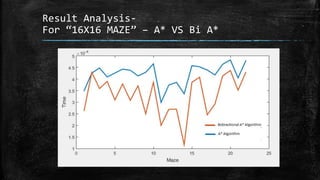
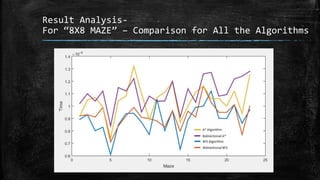
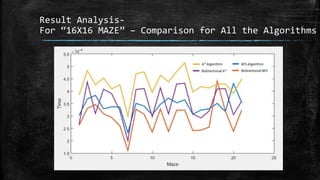
The dissertation explores bidirectional graph search techniques to find the shortest path in an image-based maze problem, detailing various algorithms such as breadth-first search (BFS), depth-first search (DFS), and A* algorithm. It includes analyses on the performance of these algorithms through image processing and pixel intensity manipulation, demonstrating how the maze is constructed and solved. The results indicate that as the size and complexity of the maze increase, so does the time needed for exploration, highlighting the importance of systematic heuristic applications in future developments.