Data structure using C :UNIT-I Introduction to Data structures and Stacks BCA SEP SEM-II

Data structure using C Unit-I BCA Semester II
1
Notes by Dr. Chandrakantha T S, Vagdevi College of BCA, Melinakuruvalli, Thirthahalli-577 432
For more notes and resources, visit: https://sites.google.com/view/chandrakanthats/bca
UNIT-I: Introduction to Data structures and Stacks
Introduction:
• Definition: A data structure is a particular way of organizing and storing data in a
computer so that it can be used efficiently.
• Data is a collection of raw facts, figures, or symbols that represent information. It can
be in the form of numbers, text, images, sounds, or any other form that can be processed
by a computer.
• Data structures help in managing large amounts of data, making programs faster and
easier to understand.
• Data structures have evolved along with computer programming. In the early days
(1950s–1960s), simple arrays and files were used to store data.
• With the development of higher-level programming languages like C and Java, more
complex structures such as linked lists, stacks, queues, trees, and graphs were
introduced to efficiently manage and process data.
File System vs Data Structure
File System Data Structure
1. Stores data in files on secondary storage
like hard disk or SSD.
1. Stores data in memory (RAM) for faster
access.
2. Access is mostly sequential, slower for
processing.
2. Access is faster, can be sequential or
random.
3. Used for long-term storage of data. 3. Used for efficient data processing and
manipulation.
4. Examples: Text files, Excel sheets, CSV
files, databases.
4. Examples: Arrays, Linked Lists, Stacks,
Queues, Trees.
5. Data is not organized in memory,
structure is limited to file format.
5. Data is organized in specific formats like
linear or non-linear structures.
6. Difficult to perform complex operations
like searching, sorting, updating
efficiently.
6. Supports complex operations like searching,
sorting, insertion, and deletion efficiently.
7. Mainly suitable for storage, backup, and
retrieval.
7. Mainly suitable for real-time processing and
algorithm implementation.

2
Need for Data Structures
1. To organize data efficiently in memory for easy access and modification.
2. To improve program performance through faster searching, insertion, deletion, and
updating of data.
3. To handle large amounts of data without affecting program efficiency.
4. To reduce software complexity by providing systematic ways to store and manage
data.
5. To facilitate algorithm implementation, making operations like sorting and searching
easier.
6. To enable reuse of code by using standard data structures in multiple programs.
Applications of Data Structures
1. Operating Systems: Process scheduling, memory management.
2. Databases: Indexing, query processing.
3. Compiler Design: Syntax analysis, symbol tables.
4. Networking: Routing tables, packet switching.
5. Artificial Intelligence & Machine Learning: Graphs for search algorithms, trees for
decision making.
6. Games & Graphics: Managing game objects, animations.
Advantages of Data Structures
1. Efficient data storage and access – Data can be stored and retrieved quickly.
2. Faster data manipulation – Searching, sorting, insertion, and deletion become easier.
3. Reduces code redundancy – Reusable structures reduce repetitive coding.
4. Helps in designing robust algorithms – Enables writing optimized and reliable
programs.
5. Supports complex operations – Facilitates operations like recursion, tree traversal,
and graph algorithms.
6. Better memory management – Efficient use of memory with dynamic allocation and
pointers.

3
Disadvantages of Data Structures
1. Requires extra memory for pointers and structure overhead.
2. Complex to implement for beginners.
3. Improper choice of data structure can reduce efficiency.
4. Maintenance of dynamic data structures can be difficult.
Types of Data Structures
• Data structures are classified based on their organization and relationship between data
elements.
• Choosing the right data structure is important for efficient data storage, access, and
manipulation.
• Broadly, data structures are of two types:
I) Primitive Data Structures
• Primitive data structures are the basic, simple data types provided by a
programming language.
• They store single values and are the building blocks for more complex data structures.
Examples of Primitive Data Structures
Data Type Description Example
1.Integer Stores whole numbers without decimals. 10, -25, 1000
2.Float Stores numbers with decimal points. 3.14, -0.5, 2.718
3.Character Stores a single alphabet, digit, or symbol. 'A', 'z', '@'
4.Boolean Stores truth values: true or false. true, false

4
II) Non-Primitive Data Structures
• Non-Primitive Data Structures are complex data structures that are built using
primitive data types.
• They can store multiple values and support advanced operations like insertion,
deletion, and traversal. These structures are used to manage large and complex data
efficiently.
Types of Non-Primitive Data Structures
a) Linear Data Structures
• Data elements are arranged in a sequential manner, one after another.
• Each element has a unique predecessor and successor (except the first and last).
Examples of Linear Data Structures
Data
Structure
Description Example / Use
1.Array Collection of elements of the same type stored
at contiguous memory locations.
Marks of 5 students: [85, 90, 78, 92, 88]
2.Linked
List
Collection of elements called nodes, where
each node contains data and a pointer to the
next node.
Student names in a list:
John → Mary → Rahul
3.Stack Linear structure following LIFO (Last In
First Out) principle.
Browser history:
Last visited page comes out first
4.Queue Linear structure following FIFO (First In
First Out) principle.
Ticket booking system:
First person in queue is served first
b) Non-Linear Data Structures
• Data elements are not arranged sequentially. One element can be
connected to multiple elements.
• Useful for representing hierarchical or interconnected relationships.
Examples of Non-Linear Data Structures
Data
Structure
Description Example / Use
1.Tree Hierarchical structure with a root node and
child nodes; each node can have zero or more
children.
Organization chart of a
company, Family tree
2.Graph Collection of nodes (vertices) connected by
edges; used to represent networks.
Social networks, Road
maps, Computer networks

5
Stacks
Definition
• Astack is a linear data structure that follows the LIFO (Last In, First Out) principle,
meaning the last element inserted is the first to be removed.
• Stacks are used in situations where reverse order processing is needed.
Example:
• A stack of plates – the last plate placed on top is the first to be taken out.
• Browser history: Last visited page is the first to go back.
Representation of Stack
A stack can be represented in two ways:
1. Array Representation
• The stack is implemented using a fixed-size array.
• A variable called top is used to keep track of the position of the top element in
the stack.
• When an element is pushed, the value of top is incremented.
• When an element is popped, the value of top is decremented.
• This method is simple and fast, but the size of the stack is fixed.

6
2. Linked List Representation
• The stack is implemented using a linked list.
• Each node contains data and a pointer to the next node.
• The top of the stack always points to the first node (last inserted element).
• Insertion and deletion are done at the beginning of the list.
• This method allows dynamic memory allocation, so stack size can grow or shrink.
Operations on Stack
• Operations on a stack are the basic actions performed to manage data stored in the stack.
• Since a stack follows the LIFO (Last In First Out) principle, all operations are
performed only at one end called the top.
• These operations help in inserting, deleting, accessing, and checking the status of
elements in the stack.
There are some basic operations that allow us to perform different actions on a stack.
• Push: Add an element to the top of a stack
• Pop: Remove an element from the top of a stack
• IsEmpty: Check if the stack is empty
• IsFull: Check if the stack is full
• Peek: Get the value of the top element without removing it

7
1. PUSH Operation (Insertion):
PUSH is the operation of inserting an element at the top of the stack.
Algorithm: PUSH
1. Start
2. Check if top == MAX – 1
o If true, display Stack Overflow and exit
3. Else, increment top by 1
4. Insert the element at stack[top]
5. Stop
MAX → Size of the stack (maximum number of elements it can store)
top → A variable that stores the index of the top element in the stack
Array Indexing Rule
In C, array index starts from 0
So for MAX = 5:
Index 0 1 2 3 4
What does top == MAX - 1 mean?
• top == MAX - 1 means
top == 4
The stack is full
So no more elements can be inserted
Before doing PUSH, we must check:
if (top == MAX - 1)
• If true → Stack is FULL → Overflow
• If false → Space is available → PUSH allowed

8
2. POP Operation (Deletion)
POP is the operation of removing the top element from the stack.
Algorithm: POP
1. Start
2. Check if top == -1
o If true, display Stack Underflow and exit
3. Else, store stack[top] in a variable
4. Decrement top by 1
5. Return the deleted element
6. Stop
3. PEEK Operation (Top Element)
PEEK operation returns the top element of the stack without removing it.
Algorithm: PEEK
1. Start
2. If top == -1
o Print “Stack is Empty”
3. Else
o Display stack[top]
4. Stop

9
4. isEmpty Operation
isEmpty checks whether the stack contains any elements.
Algorithm: isEmpty
1. Start
2. If top == -1
o Return TRUE
3. Else
o Return FALSE
4. Stop
5. isFull Operation
isFull checks whether the stack is completely filled.
Algorithm: isFull
1. Start
2. If top == MAX - 1
o Return TRUE
3. Else
o Return FALSE
4. Stop
Applications of Stack
1. Function Calls and Recursion: Stack is used to store function calls, local variables,
and return addresses during program execution.
2. Expression Evaluation: Stacks are used to evaluate arithmetic expressions like postfix
and prefix expressions.
3. Expression Conversion: Used to convert expressions from infix to postfix or prefix
form.
4. Syntax Parsing in Compilers: Compilers use stacks to check syntax and match
parentheses.
5. Undo and Redo Operations: Applications like text editors use stacks to implement
undo and redo features.
6. Backtracking Algorithms: Used in problems like maze solving and depth-first search
(DFS).
7. Reversing Data: Stack is used to reverse strings, arrays, or lists.
8. Browser History: Web browsers use stacks to track visited web pages.

10
Expression Notations
• Expression notations specify the position of operators and operands in an expression.
• They are used to represent and evaluate mathematical and logical expressions.
• Different notations help computers process expressions efficiently.
• The commonly used expression notations are Infix, Prefix, and Postfix.
1. Infix Notation
• Infix notation is a way of writing expressions in which the operator is placed between
the operands.
• It is the most commonly used notation in mathematics and everyday calculations.
• Parentheses are often required to show the order of operations.
• It is easy for humans to understand but difficult for computers to evaluate directly.
Examples:
A + B
5 * 6
(A + B) * C
2. Prefix Notation (Polish Notation)
• Prefix notation is a way of writing expressions in which the operator is placed before
the operands. It is also known as Polish Notation.
• Parentheses are not required.
• Easy for computers to evaluate using stacks.
Examples:
+ A B
* 5 6
* + A B C
3. Postfix Notation (Reverse Polish Notation)
• Postfix notation is a way of writing expressions in which the operator is placed after
the operands. It is also known as Reverse Polish Notation (RPN).
• Parentheses are not required.
• Very easy for computers to evaluate using stacks.

11
Examples:
A B +
5 6 *
A B C * +
Operator Precedence
• Operator precedence defines the order in which operators are evaluated in an
expression.
Order Operator Description Precedence Level
1 ^ Exponentiation Highest
2 * Multiplication Medium
3 / Division Medium
4 + Addition Lowest
5 - Subtraction Lowest
• Operators with higher precedence are evaluated before operators with lower
precedence.
• Parentheses () can be used to change the order of evaluation.
• Operator precedence is important while converting infix expressions to postfix or
prefix.
Examples of Operator Precedence
Example 1:
A + B * C
Order:
• B * C (multiplication first)
• A + (B * C)
Example 2:
A + B * C ^ D
Order:
• C ^ D (exponentiation first)
• B * (C ^ D)
• A + [result]

12
Example 3:
A + B * C - D / E ^ F
Order of Evaluation:
1. E ^ F → Exponentiation (highest precedence)
2. B * C → Multiplication
3. D / (E ^ F) → Division
4. A + (B * C) → Addition
5. [result] - [result] → Subtraction
Final Grouped Expression: (A + (B * C)) - (D / (E ^ F))
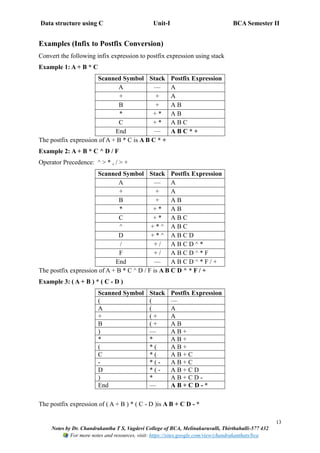
Evaluation of postfix expression using stack
• Conversion of an infix expression to postfix expression is done using a stack to handle
operators and parentheses.
• This method follows operator precedence and associativity rules to maintain the
correct order of operations.
• Postfix expressions are easier for computers to evaluate using stacks.
Algorithm: Infix to Postfix Conversion using Stack
1. Start
2. Initialize an empty stack and an empty postfix expression.
3. Scan the infix expression from left to right.
4. If the symbol is an operand, add it to the postfix expression.
5. If the symbol is (, push it onto the stack.
6. If the symbol is ), pop operators from the stack and add them to postfix until ( is found;
discard both parentheses.
7. If the symbol is an operator:
o Pop operators from the stack that have higher or equal precedence.
o Push the current operator onto the stack.
8. After the complete expression is scanned, pop all remaining operators from the stack
and add them to postfix.
9. Stop

13
Examples (Infix to Postfix Conversion)
Convert the following infix expression to postfix expression using stack
Example 1: A + B * C
Scanned Symbol Stack Postfix Expression
A — A
+ + A
B + A B
* + * A B
C + * A B C
End — A B C * +
The postfix expression of A + B * C is A B C * +
Example 2: A + B * C ^ D / F
Operator Precedence: ^ > * , / > +
A — A
+ + A
B + A B
* + * A B
C + * A B C
^ + * ^ A B C
D + * ^ A B C D
/ + / A B C D ^ *
F + / A B C D ^ * F
End — A B C D ^ * F / +
The postfix expression of A + B * C ^ D / F is A B C D ^ * F / +
Example 3: ( A + B ) * ( C - D )
( ( —
A ( A
+ ( + A
B ( + A B
) — A B +
* * A B +
( * ( A B +
C * ( A B + C
- * ( - A B + C
D * ( - A B + C D
) * A B + C D -
End — A B + C D - *
The postfix expression of ( A + B ) * ( C - D )is A B + C D - *

14
Example 4: A + ( B * C - D ) / E
A — A
+ + A
( + ( A
B + ( A B
* + ( * A B
C + ( * A B C
- + ( - A B C *
D + ( - A B C * D
) + A B C * D -
/ + / A B C * D -
E + / A B C * D - E
End — A B C * D - E / +
The postfix expression of A + ( B * C - D ) / E is A B C * D - E / +
Example 5: ( A + B ) * C ^ ( D - E ) / F
( ( —
A ( A
+ ( + A
B ( + A B
) — A B +
* * A B +
C * A B + C
^ * ^ A B + C
( * ^ ( A B + C
D * ^ ( A B + C D
- * ^ ( - A B + C D
E * ^ ( - A B + C D E
) * ^ A B + C D E -
/ / A B + C D E - ^ *
F / A B + C D E - ^ * F
End — A B + C D E - ^ * F /
The postfix expression of ( A + B ) * C ^ ( D - E ) / F is A B + C D E - ^ * F /

15
Recursive Function
Definition
A recursive function is a function that calls itself to solve a problem. It breaks a large problem
into smaller sub-problems and continues until a base condition is satisfied.
• A recursive function must have a base case to stop execution.
• Without a base case, the function will result in infinite recursion.
• Recursion uses a stack to store function calls.
Advantages of Recursion
1. Makes the program simple and easy to understand.
2. Reduces code length compared to iterative solutions.
3. Useful for problems that can be divided into smaller sub-problems.
4. Well suited for tree traversal and divide-and-conquer algorithms.
5. Improves clarity in problems like factorial, Fibonacci, and quick sort.
Disadvantages of Recursion
1. Uses more memory due to function call stack.
2. Slower execution compared to loops.
3. Difficult to debug and trace recursive calls.
4. Risk of stack overflow if base condition is missing or incorrect.
5. Not suitable for all problems, especially simple repetitive tasks.
Example 1: Factorial of a Number
The factorial of a number is the product of all positive integers from 1 to that number.
It is denoted by the symbol !.
Mathematical Definition
n!=n×(n−1)×(n−2)×⋯×1
Special Case: 0!=1
Example: 5!=5×4×3×2×1=120

16
Algorithm: Factorial of a Number Using Recursion
1. Start
2. Read the value of n.
3. Call the recursive function factorial(n).
4. In the factorial function:
o If n == 0, return 1 (base condition).
o Else return n * factorial(n − 1) (recursive call).
5. Display the returned value as the factorial of the number.
6. Stop
Factorial of a Number Recursive Function in C
#include <stdio.h>
int factorial(int n) // Recursive function to calculate factorial of a number
{
if (n == 0) // Base condition: factorial of 0 is 1
{
return 1;
}
else
{
return n * factorial(n - 1); // Recursive call: n * factorial of (n-1)}
}
int main()
{
int n = 5; // Number whose factorial is to be calculated
printf("Factorial = %d", factorial(n)); // Calling factorial function
return 0;
}
Output: Factorial = 120

17
Example 2: Fibonacci Series
The Fibonacci series is a sequence of numbers in which each number is the sum of the two
preceding numbers. The series starts with 0 and 1.
Mathematical Definition:
F(0)=0, F(1)=1
F(n)=F(n−1)+F(n−2),for n≥2
Example:
Fibonacci series up to 6 terms: 0, 1, 1, 2, 3, 5
Applications of Fibonacci Series
1. Algorithm Design – Used in Fibonacci Search for faster searching in arrays.
2. Data Structures – Applied in Fibonacci Heap to optimize priority queue operations.
3. Recursion Practice – Helps explain recursive functions in programming.
4. Dynamic Programming – Example: calculating nth Fibonacci number efficiently.
5. Mathematical Patterns – Appears in Pascal’s triangle and number theory.
6. Real-Life Modeling – Models population growth, rabbit reproduction, and
branching in trees.
Algorithm: Fibonacci Series Using Recursion
1. Start
2. Read the value of n (number of terms).
3. For i = 0 to n − 1, call fibonacci(i) and print the value.
4. In the fibonacci function:
o If n == 0, return 0.
o If n == 1, return 1.
o Else return fibonacci(n − 1) + fibonacci(n − 2).
5. Stop

18
Fibonacci Series Using Recursive Function in C
#include <stdio.h>
// Recursive function to find Fibonacci number
int fibonacci(int n)
{
if (n == 0)
{
return 0; // Base condition
}
else if
{
(n == 1)
return 1; // Base condition
}
else
{
return fibonacci(n - 1) + fibonacci(n - 2); // Recursive call
}
}
int main()
{
int n = 6; // Number of terms
printf("Fibonacci Series:n");
// Printing Fibonacci series
for (int i = 0; i < n; i++)
{
printf("%d ", fibonacci(i));
}
return 0;
}
Output: Fibonacci Series: 0 1 1 2 3 5
*** ** ***

Data structure using C :UNIT-I Introduction to Data structures and Stacks BCA SEP SEM-II

More Related Content

Similar to Data structure using C :UNIT-I Introduction to Data structures and Stacks BCA SEP SEM-II

More from Kuvempu University

Recently uploaded

Data structure using C :UNIT-I Introduction to Data structures and Stacks BCA SEP SEM-II