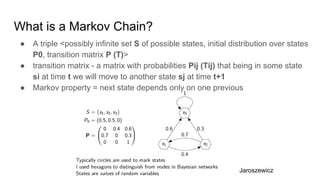
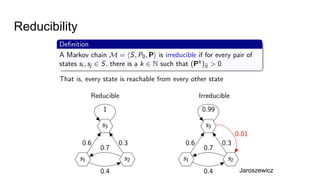
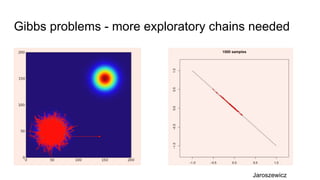
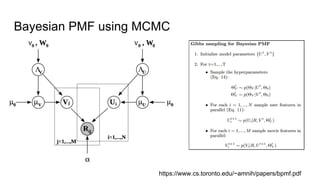
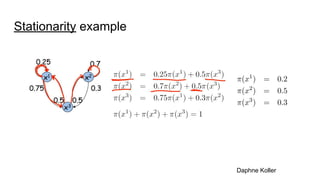
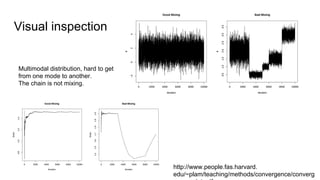
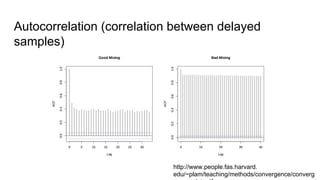
- The document discusses various techniques for Markov chain Monte Carlo (MCMC) sampling, including rejection sampling, Metropolis-Hastings, and Gibbs sampling. - It explains how MCMC can be used for approximate probabilistic inference in complex models by constructing a Markov chain that converges to the target distribution. - Diagnostics are discussed for checking if the Markov chain has converged, such as visual inspection of trace plots, and Geweke and Gelman-Rubin tests of the within-chain and between-chain variances.

1. Part 1: 2016-01-20
Part 2: 2016-02-10
Tomasz Kuśmierczyk
Session 5: Sampling & MCMC
Approximate and Scalable Inference for Complex
Probabilistic Models in Recommender Systems
Part 2: Inference Techniques

2. MCMC = Monte Carlo Markov Chains
MCMC ⊂ Sampling

3. Literature / Credits
● Szymon Jaroszewicz lectures on “Selected Advanced Topics in Machine Learning”
● Daphne Koller lectures on “Probabilistic Graphical Models” (https://class.coursera.
org/pgm-003/lecture)
● Patrick Lam slides http://www.people.fas.harvard.
edu/~plam/teaching/methods/convergence/convergence_print.pdf
● Bishop’s book ch. 11
● MacKay, David JC. Information theory, inference and learning algorithms. Cambridge
university press, 2003. (http://www.inference.phy.cam.ac.uk/itprnn/book.pdf)
● R & JAGS online tutorials…
● …

4. Basics & motivation

5. Motivation: Monte Carlo for integrating
http://mlg.eng.cam.ac.uk/zoubin/tut06/mcmc.pdf
Non-trivial posterior
distribution (e.g., for BNs)

6. Sampling vs Variational Inference (previous seminar)
http://people.inf.ethz.ch/bkay/talks/Brodersen_2013_03_22.pdf

7. Sampling continued ...
● Accuracy of sampling based estimates depends only on the variance of the
quantity being estimated
● It does not depend directly on the dimensionality (having many variables is
not a problem)
● In some cases we are able to break the curse of dimensionality
but
● Sampling gets much more difficult in higher dimensions
● Variance often increases as the dimension grows
● Accuracy of sampling based methods grows only with square root of the
number of samples
Jaroszewicz

8. Sampling techniques - basic cases
● uniform -> pseudo-random numbers generator
● discrete distributions -> range matching with the help of uniform (in log of
number of outcomes time)
● continous -> cdf inverse
● various ‘tricks’
● ...

9. Sampling techniques (e.g., for BNs posterior)
● Ancestral Sampling (no evidence)
● Probabilistic Logic Sampling (like AS but samples not consistent with
evidence are discarded -> low number of samples generated)
● Likelihood weighting (estimations may be inaccurate + other problems)
● Importance Sampling
● (Adaptive) Rejection Sampling
● Sampling-Importance-Resampling
● Metropolis
● Metropolis-Hastings
● Gibbs Sampling
● Hamiltionian (hybrid) Sampling
● Slice sampling
● and more...

10. Monte Carlo without Markov Chains

11. Few remarks
● there is no difference between sampling from normalized and non-normalized
distributions
● non-normalized distributions are easy to evaluate for BNs
● in most cases (e.g. rejection sampling) we work with non-normalized
distributions
● for simplicity p(x) is used in notation but there is no difference for complicated
posterior distributions
● 1D case presented but work also in multi-dimensional case.

12. Rejection sampling
Jaroszewicz, Bishop
c q(x)
p(x)

13. Rejection sampling - proof
Jaroszewicz

14. Selection of c?
● c should be as small as possible to have low reduction rate
● but p <= c q must hold
● Adaptive Rejection Sampling for log-concave distributions
○ log-concave = logarithm of the distribution is concave

15. Adaptive Rejection Sampling
Jaroszewicz

16. Rejection Sampling problems
● part of the samples are rejected
● tight “envelope” helps a bit
but
● in many dimensions (when there are many variables) dimensionality curse
must be taken into account
● see Bishop’s example (for rejection sampling):
○ p(x) ~ N(0, s1)
○ q(x) ~ N(0, 1.01*s1)
○ D=1000
○ -> acceptance ratio 1/20000

17. Markov Chains

18. What is a Markov Chain?
● A triple <possibly infinite set S of possible states, initial distribution over states
P0, transition matrix P (T)>
● transition matrix - a matrix with probabilities Pij (Tij) that being in some state
si at time t we will move to another state sj at time t+1
● Markov property = next state depends only on one previous
Jaroszewicz

19. Markov Chains - distribution over states
Jaroszewicz

20. Markov Chains - stationary distribution
Jaroszewicz

21. Stationarity example
Daphne Koller

22. Stationarity from regularity
● If there exists k such that, for every two states <si, sj> the probability of
getting from si to sj in exactly k steps is > 0 (MC is regular) →MC converges
to a unique stationary distribution
● Sufficient conditions for regularity:
○ there is a path between every pair of states
○ for every state, there is a self-transition

23. Stationarity of irreducible, aperiodic MC
● Irreducible, aperiodic Markov chains always converge to a unique stationary
distribution

24. Reducibility
Jaroszewicz

25. Periodicity
Jaroszewicz

26. Why I talk about Markov Chains -> MCMC
the idea is that:
● Markov Chain “jumps” over states
● states determine (BN) samples (that are later used for Monte Carlo)
○ for example: state ⇔ sample
but we need:
● Markov Chain converges to a stationary distribution (to be proved every time)
● a distribution of generated samples is equal to required distribution (BNs
posterior)

27. Properties
● Very general purpose
● Often easy to implement
● Good theoretical guarantees as t -> ∞
but:
● Lots of tunable parameters / design choices
● Can be quite slow to converge
● Difficult to tell whether it’s working

28. Metropolis-Hastings derivation
on the blackboard:
1. From detailed balance to stationarity
2. Proposed distribution and acceptance probability
3. From detailed balance to conditions on acceptance probability

29. Part 2
Dawn of Statistical Renaissance

30. Gibbs sampling

31. Gibbs sampling: Algorithm
Daphne Koller

32. Does it work? - often
Under certain conditions, the stationary distribution of this Markov chain is the joint
distribution of the Bayesian network:
● A probability distribution P(X) is positive, if P(X = x) > 0 for all x ∈ Dom(X).
● Theorem: If all conditional distributions in a Bayesian network are positive
(all probabilities are > 0) then a Gibbs sampler converges to the joint
distribution of the Bayesian network.

33. Gibbs properties
● Can handle evidence even with very low probability
● Works for all kinds of models, e.g. Markov networks, continuous variables
● Works very well in many practical cases
● overall is a very powerful and useful technique
● very popular nowadays
● has become another Swiss army knife for probabilistic inference
but
● Samples not statistically independent (statistics gets difficult)
● Hard to give guarantees on results
Jaroszewicz

34. Gibbs problems - more exploratory chains needed
Jaroszewicz

35. Gibbs sampling: example

36. Bayesian PMF using MCMC
https://www.cs.toronto.edu/~amnih/papers/bpmf.pdf

37. Bayesian PMF using MCMC
Some useful formulas:
on the blackboard ...

38. Diagnostics

39. You never know with randomness...

40. Practical problems
● We only want to use samples that are sampled from a distribution close to p
(x) - when chain is already ‘mixing’
● At early iterations (before chain converged) we may be far from p(x) - we
need ‘burn-in’ iterations
● Samples are correlated - we need thinning (take only every n-th sample)

41. Diagnostics
● Visual Inspection
● Geweke Diagnostic
○ tests whether the burn-in is sufficient
● Gelman and Rubin Diagnostic
○ may detect problems with disconnected sample spaces
● Raftery and Lewis Diagnostic
○ calculates the number of iterations and burn-in needed by first running
● Heidelberg and Welch Diagnostic
○ test statistic for stationarity of the distribution
http://www.people.fas.harvard.edu/~plam/teaching/methods/convergence/convergence_print.pdf

42. Visual inspection
http://www.people.fas.harvard.
edu/~plam/teaching/methods/convergence/converg
Multimodal distribution, hard to get
from one mode to another.
The chain is not mixing.

43. Autocorrelation (correlation between delayed
samples)
http://www.people.fas.harvard.
edu/~plam/teaching/methods/convergence/converg

44. Geweke Diagnostic
● takes two nonoverlapping parts of the Markov chain
● compares the means of both parts, using a difference of means test
● to see if the two parts of the chain are from the same distribution (null
hypothesis).
● the test statistic is a standard Z-score with the standard errors adjusted for
autocorrelation.

45. Gelman and Rubin Diagnostic
1. Run m ≥ 2 chains of length 2n from overdispersed starting values.
2. Discard the first n draws in each chain.
3. Calculate the within-chain and between-chain variance.
http://www.people.fas.harvard.
edu/~plam/teaching/methods/convergence/converg

46. Gelman and Rubin Diagnostic 2
4. Calculate the estimated variance of the parameter as a weighted
sum of the within-chain and between-chain variance.
5. Calculate the potential scale reduction factor.
When R is high (perhaps greater than 1.1 or 1.2), then we should run our
chains out longer to improve convergence to the stationary distribution.
http://www.people.fas.harvard.
edu/~plam/teaching/methods/convergence/converg

47. Probabilistic programming

48. Probabilistic programming language
programming language designed to:
● describe probabilistic models
● perform inference automatically even on complicated models
for example:
● PyMC
● BUGS / JAGS
● BayesPy
https://en.wikipedia.org/wiki/Probabilistic_programming_language

49. What’s inside?
● BUGS - Adaptive Rejection (AR) sampling
● JAGS - Slice Sampler (one variable at once)

50. JAGS PMF-like example: model file
model{#########START###########
sv ~ dunif(0,100)
su ~ dunif(0,100)
s ~ dunif(0,100)
tau <- 1/(s*s)
tauv <- 1/(sv*sv)
tauu <- 1/(su*su)
...
...
for (j in 1:M) {
for (d in 1:D) {
v[j,d] ~ dnorm(0, tauv)
}
}
for (i in 1:N) {
for (d in 1:D) {
u[i,d] ~ dnorm(0, tauu)
}
}
for (j in 1:M) {
for (i in 1:N) {
mu[i,j] <- inprod(u[i,], v[j,])
r3[i,j] <- 1/(1+exp(-mu[i,j]))
r[i,j] ~ dnorm(r3[i,j], tau)
}
}
}#############END############

51. JAGS PMF-like example: Parameters preparation
n.chains = 1
n.iter = 5000
n.burnin = n.iter
n.thin = 1 #max(1, floor((n.iter - n.burnin)/1000))
D = 10
lu = 0.05
lv = 0.05
n.cluster=n.chains
model.file = "models/pmf_hypnorm3.bug"
N = dim(train)[1]
M = dim(train)[2]
start.s = sd(train[!is.na(train)])
start.su = sqrt(start.s^2/lu)
start.sv = sqrt(start.s^2/lv)
jags.data = list(N=N, M=M, D=D, r=train)
jags.params = c("u", "v", "s", "su", "sv")
jags.inits = list(s=start.s, su=start.su, sv=start.sv,
u=matrix( rnorm(N*D,mean=0,sd=start.su), N, D),
v=matrix( rnorm(M*D,mean=0,sd=start.sv), M, D))

52. JAGS PMF-like example: running (sampling)
library(rjags)
model = jags.model(model.file, jags.data, n.chains=n.chains, n.adapt=n.burnin)
#update(model)
samples = jags.samples(model, jags.params, n.iter=n.iter, thin=n.thin)

53. JAGS PMF-like example: retrieving samples
per.chain = dim(samples$u)[3]
iterations = per.chain * dim(samples$u)[4]
user_sample = function(i, k) {samples$u[i, , (k-1)%%per.chain+1, ceiling(k/per.chain)]}
item_sample = function(j, k) {samples$v[j, , (k-1)%%per.chain+1, ceiling(k/per.chain)]}

54. Why it’s good, why it’s bad?
● fast prototyping
● less control

55. Results on movielens 100k
RMSE = 0.943 (~SGD)
More on https://github.com/tkusmierczyk/pmf-jags

56. Thank you!