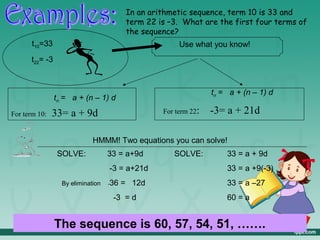
The document defines an arithmetic sequence as a sequence where a constant difference can be added between each term to get the next term. It provides examples of finding the first term and common difference of arithmetic sequences. It explains that the common difference is found by subtracting any term from the one that follows it. Formulas are provided for finding specific terms in an arithmetic sequence given the first term, common difference, or other information. Examples problems are worked through applying these concepts.

1. Sequence

3. Objectives
1. Define Arithmetic
Sequence
2. Determine if a sequence
is an Arithmetic
3. Determine the first term
and common difference

4. A sequence in which
a constant (d) can
be added to each
term to get the
next term is called
an
Arithmetic
Sequence.

5. The
constant (d)
is called the
COMMON
DIFFERENCE.

6. Common Difference.
To find the common
difference (d), subtract
any term from one that
follows it.
a1 a2 a3 a4 a5
2 5 8 11 14
3 3 3 3

7. Find the first term
and the common
1.) 4, 9, 14, 19, 24 difference of each
arithmetic
First term (a1): 4
Common difference sequence. = 9 – 4 = 5
a2 _ a1
(d):
1.) 34, 27, 20, 13, 6, -1,-8
First term (a1): 34
Common difference (d): -7
BE CAREFUL: ALWAYS CHECK TO MAKE
SURE THE DIFFERENCE IS THE SAME
BETWEEN EACH TERM !

8. Find the first term
and the common
1.) 4, 9, 14, 19, 24 difference of each
arithmetic
First term (a1): 4
Common difference sequence. = 9 – 4 = 5
a2 _ a1
(d):
1.) 34, 27, 20, 13, 6, -1,-8
First term (a1): 34
Common difference (d): -7
BE CAREFUL: ALWAYS CHECK TO MAKE
SURE THE DIFFERENCE IS THE SAME
BETWEEN EACH TERM !

9. Which of the following sequences are
arithmetic? Identify the common
difference.
−3, − 1, 1, 3, 5, 7, 9, . . . YES d =2
15.5, 14, 12.5, 11, 9.5, 8, . . . YES d = −1.5
84, 80, 74, 66, 56, 44, . . . NO
−8, 6, − 4, 2, 0, . . . NO
−50, − 44, − 38, − 32, − 26, . . . YES d = 6

10. The common
d ifference is always -21-(-26) = 5
the difference between -21+26 = 5
any term and the term Common
that precedes tha t Difference =
5
term.
−26, − 21, − 16, − 11, − 6, . . .

11. An Arithmetic Sequence is
defined as a sequence in
which there is a common
difference between
consecutive terms.

12. Fixed Consecutiv
Pattern e Terms
Common Succession
Addition
difference
Arithmetic
sequence

13. Assignment!
Find the first term and the common
difference of each of these arithmetic
sequences.
a) 1, -4, -9, -14, ….
b) 11, 23, 35, 47, ….
c) 3x-8, x-8, -x-8, -3x-8
d) s-4, 3s-3, 5s-2, 7s-1, …..

14. Answers with solutions
a) 1, -4, -9, -14, …. a=1 and
d = a2 - a1 = - 4 - 1 = - 5
b) 11, 23, 35, 47, …. a = 11 and
d = a2 - a1 = 23 - 11 = 12
c) 3x-8, x-8, -x-8, -3x-8 a = 3x-8 and
d = a2 - a1 = x – 8 – (3x – 8) = - 2x
a=s-4 and
d) s-4, 3s-3, 5s-2, 7s-1, …..
d = a2 - a1 = 3s – 3 – (s – 4) = 2s + 1

15. The first term of an arithmetic sequence
is (a) . We add (d) to get the next term.
There is a pattern, therefore there is a
formula we can use to give use any term
that we need without listing the whole
sequence .
3, 7, 11, 15, …. We know a = 3 and d = 4
t1= a = 3
t2= a+d = 3+4 = 7
t3= a+d+d = a+2d = 3+2(4) = 11
t4 = a+d+d+d = a+3d = 3+3(4) = 15

16. The first term of an arithmetic sequence
is (a) . We add (d) to get the next term.
There is a pattern, therefore there is a
formula we can use to give use any term
that we need without listing the whole
sequence .
The nth term of an arithmetic sequence is given by:
tn = a + (n – 1) d
The last # in the The position the
First
sequence/or the # you term is in
term The common
are looking for
difference

17. Find the 14th term of the
arithmetic sequence
4, 7, 10, 13,……
tn = a + (n – 1) d
t14 = 4 +(14 −1) 3 You are
= 4 + (13)3 looking for
the term!
= 4 + 39
= 43 The 14th term in this
sequence is the number

18. Now you try!
Find the 10th and 25th term given the following information. Make sure to
derive the general formula first and then list ehat you have been provided.
a) 1, 7, 13, 19 ….
b) x+10, x+7, x+4, x+1, ….
c) The first term is 3 and the common difference is -21
d) The second term is 8 and the common difference is 3

19. Answers with solutions
a=1 and d = a2 - a1 = 7 – 1 = 6
a) 1, 7, 13, 19 ….
…. tn=a+(n-1)d = 1 + (n-1) 6 = 1+6n-6 So tn = 6n-5
t10 = 6(10) – 5 = 55
t25 = 6(25)-5 = 145
b) x+10, x+7, x+4, a = x+10 and d = a2 - a1 = x+7-(x+10) = -3
x+1,.
tn=a+(n-1)d = x+10 + (n-1)(-3) = x+10-3n+3 So tn= x-
3n+13
t10 = x -3(10)+13 = x - 17
c) The first term is 3 andt25 = x a = 3 and xd- 62-21
the -3(25)+13 =
=
common difference is -21 tn=a+(n-1)d = 3 + (n-1) -21 = 3-21n+21 So tn= 24-21n
t10 = 24-21(10) = -186 t25 = 24-21(25) = -501
d) The second term is 8 a=8-3 =5 and d =3
and the common
difference is 3
tn=a+(n-1)d = 5 + (n-1) 3 = 5+3n-3 So tn = 3n+2
t10 = 3(10) +2 = 32 t25 = 3(25)+2 = 77

20. Find the 14th term of the arithmetic sequence
with first term of 5 and the common difference
is –6.
a = 5 and d = -6
You are looking for the
tn = a + (n – 1) d term! List which
variables from the
t14 = 5 +(14 −1) -6
general term are
provided!
= 5 + (13) * -6
= 5 + -78
= -73
The 14th term in this
sequence is the number

21. In the arithmetic sequence
4,7,10,13,…, which term has a
value of 301?
tn = a + (n – 1) d
301 = 4 + ( n − 1)3 You are
301 = 4 + 3n − 3 looking
301 = 1 + 3n for n!
300 = 3n
100 = n The 100th term in this
sequence is 301!

22. In an arithmetic sequence, term 10 is 33 and
term 22 is –3. What are the first four terms of
the sequence?
t10=33 Use what you know!
t22= -3
tn = a + (n – 1) d
tn = a + (n – 1) d
For term 10: 33= a + 9d For term 22: -3= a + 21d
HMMM! Two equations you can solve!
SOLVE: 33 = a+9d SOLVE: 33 = a + 9d
-3 = a+21d 33 = a +9(-3)
By elimination - 36 = 12d 33 = a –27
-3 = d 60 = a
The sequence is 60, 57, 54, 51, …….

23. Review

24. 1. Variable M varies
directly with p.
If M = 75 when p =
10,
find M when p = 16.

25. Write formula:
Find constant:
Find new value:
NEXT

27. Drill