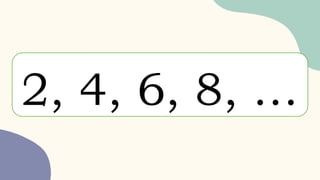
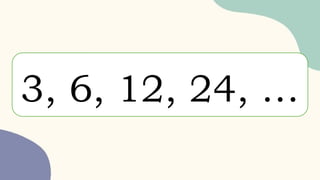
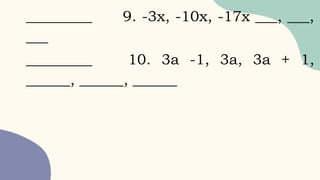The document explains arithmetic sequences, which are sequences formed by adding a fixed number called the common difference to each preceding term. It provides examples and exercises to find the common difference, next terms, and specific nth terms within such sequences. Additionally, it discusses how to calculate arithmetic means and deal with missing terms related to given sequences.

1. Illustrating an
Arithmetic
Sequence

2. 2, 4, 6, 8, …

3. 3, 6, 12, 24, …

4. 5, 10, 15, 20, …

5. Observe the following
sequences:
1.4, 7, 10, 13, …
2.33, 38, 43, 48, …
3.-2, -6, -10, -14, …
4.100, 98, 96, 94, …

6. Notice that to get the next
term in each of the
sequences above, a constant
or a common number is
added to the preceding term
or the number before it.

7. A sequence in which term after
the first is formed by adding a
fixed number to the preceding
term is called arithmetic
sequence. The fixed number or
constant is called the common
difference denoted by .
Arithmetic Sequences

8. To find the common
difference (d), you can simply
subtract
the second term by the first
term ,
- ,

9. Example 1
Determine if the sequence is
arithmetic or not. If it is, find
the common difference and
the next three terms of the
sequence.
-4, 3, 10, 17, …

10. Example 2
Write the first five terms of
the arithmetic sequence
with 5 as the first term and
with a common difference
of -2.

11. Example 3
Find the common difference
of the arithmetic sequence

12. I was advised by my physician to walk
each day in the morning as a daily
exercise. On the first day, I walked
40m. On the second and third day, I
walked 60m and 80m, respectively,
and so on. Which of the following is
the distance I walked on the 10th
day
if I continue the pattern in my daily
walk?

13. Activity:
Find the common difference and the next
three terms of each arithmetic sequence.
Write your answer on your answer sheet.
Common Difference Next 3 Terms
_________ 1. 24, 14, 4, ___, ___, ___
_________ 2. 6, 10, 14, ___, ___, ___

14. _________ 3. -7, 4, 15, ___, ___, ____
_________ 4. 21, 15, 9, ___, ___, ___
_________ 5. -8, -6, -4, ___, ___, ___
_________ 6. 5, -1, -7, ___, ___, ___
_________ 7. 4.1, 11.1, 18.1, ___, ___,
___
_________ 8. -1, -8, -15, ___, ___, ___

15. _________ 9. -3x, -10x, -17x ___, ___,
___
_________ 10. 3a -1, 3a, 3a + 1,
______, ______, ______

16. Arithmetic Means
and Term of an
Arithmetic
Sequence

17. Given the sequence 3,
8, 13, 18,…; what is
the 15th
term?

18. The nth
term of an arithmetic
sequence with first term a1
and common difference d is
given by:
an = a1 + d (n-1)

19. where:
an is the term that
corresponds to nth
position,
a1 is the first term, and
d is the common difference.

20. Example 1
Find the 21st
term of the
arithmetic sequence: 6,
9, 12, 15,…

21. Example 2
The 3rd
term of an
arithmetic sequence is 8
and the 16th
term is 47.
Find d, and the 71st
term.

22. Activity: Write answer on your
answer sheet.
A.Find the specified nth
term of
each arithmetic sequence.
_________1. 2, 5, 8, …; 9th
term
_________ 2. 3, 5 7, …; 20th
term
_________ 3. 5, 11, 17, …; 9th
term

23. _______ 4. 26, 22, 18, …; 40th
term
_______ 5. 103rd
term of the
arithmetic sequence if = -5 and d =
-4
_______ 6. 19th
term of the arithmetic
sequence if = 25 and d = -2
_______ 7. In the sequence 2, 6, 10,
…; find n if the nth
term is 102.

24. Computing
Arithmetic
Means

25. 4, 8, 12, 16, 20, 24;

26. The first and last terms of a finite
arithmetic sequences are called
arithmetic extremes, and the terms in
between are called arithmetic means. In
the sequence 4, 8, 12, 16, 20, 24; the
terms 4 and 24 are the arithmetic
extremes, while 8, 12, 16, and 20 are the
arithmetic means. Also, 8 is the arithmetic
mean of the arithmetic extremes, 4 and
12.

27. The formula for, d can be used
to find the arithmetic means if
more than one arithmetic means
will be inserted between two
arithmetic extremes.

28. Activity 1: Using the example above,
solve for the arithmetic mean of
each of the pairs of arithmetic
extremes. Write your answer on
your answer sheet.
86, _____, 45 125, _____, 60
135, _____, 170 43, _____, 89
50, _____, - 30

29. 1. Insert three arithmetic
means between 8 and 16.
2. Find the missing terms of
the arithmetic sequence:
_____, 6, _____, _____, 30.

30. Activity 2: Find the missing terms of
the following sequence. Write
answer on your answer sheet.
1. 15, _____, _____, _____, _____, 45
2. _____, 7, 13, _____, _____
3. _____, 4, _____, 18, _____
4. _____, 9, _____, _____, 36
5. 16, _____, _____, _____, 32