Embed presentation
Downloaded 40 times
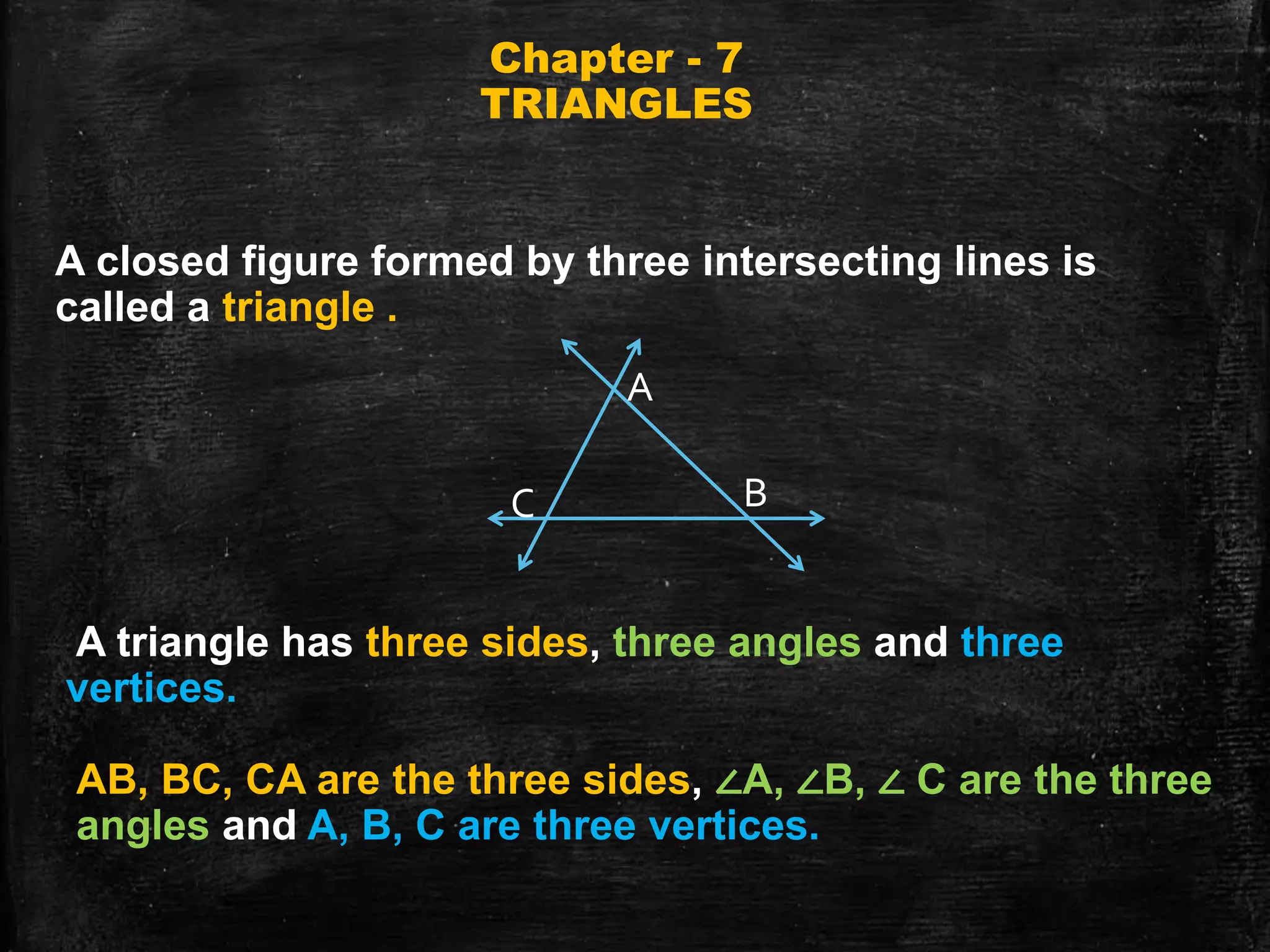
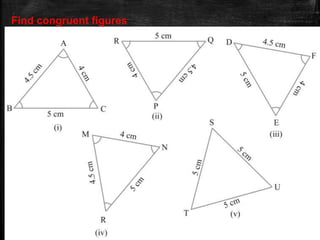





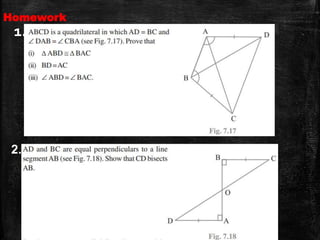
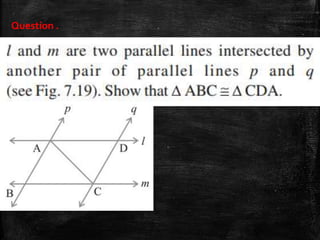

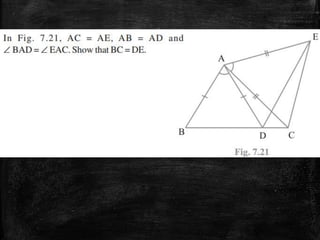
This document discusses triangles and congruence. It defines a triangle as a closed figure with three intersecting lines and as having three sides, three angles, and three vertices. It then explains the meaning of congruence as equal in all respects and introduces three rules for determining if triangles are congruent: the Side-Angle-Side rule, the Angle-Side-Angle rule, and the Angle-Angle-Side rule. The document concludes with assigning homework questions involving congruent triangles.











