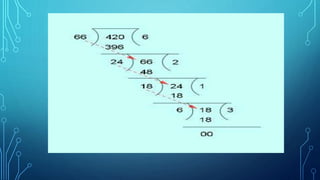
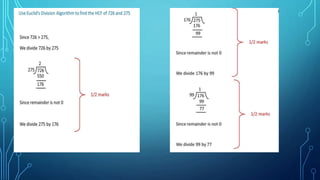
This document provides an overview of key topics in mathematics including real numbers, prime factorization, rational and irrational numbers, and properties of the highest common factor (HCF) and lowest common multiple (LCM). Some key points covered include: - The fundamental theorem of arithmetic which states that every composite number can be uniquely factored into prime numbers. - Examples of factorizing numbers into their prime factors and using this to find the HCF and LCM of pairs of numbers. - The definition of rational and irrational numbers and examples of each, including proofs that √5 is irrational. 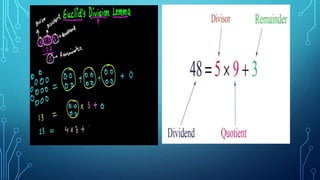- Properties of HCF and LCM, including that HCF × LCM = the product of the two original numbers.

1. GLORY ENGLISH MEDIUM
SCHOOL
SUBJECT: MATHEMATICS
CLASS: 10TH
TOPIC:REAL NUMBER(CHAPTER 1)
PRESENTED BY
POOJA VAISH

2. EUCLIDS DIVISION LEMMA

7. EUCLID’S DIVISION ALGORITHM

11. THE FUNDAMENTAL THEOREM OF
ARITHMATIC
The fundamental theorem of arithmetic -states, "Every
composite number can be factorized as a product of
primes, and this factorization is unique, apart from the
order in which the prime factors occur".
This is also called unique factorization theorem.
So we have factorised 1092 as 2*3*2*7*13 as a product of
prime.
Qu: Express each no as a product of its prime factor.
(i) 140
By Taking the LCM of 140, we will get the product of its
prime factor.
Therefore, 140 = 2 × 2 × 5 × 7 × 1 = 22×5×7
(ii) 156
By Taking the LCM of 156, we will get the product of its
prime factor.

12. HCF(A,B)=PRODUCT OF THE SMALLEST POWER OF EACH COMMON PRIME
FACTORS IN THE NUMBERS
LCM(A,B)=PRODUCT OF THE GREATEST POWER OF EACH PRIME FACTOR
INVOLVED IN NUMBERS
FOR ANY TWO POSITIVE INTEGAR ,HCF(A,B)*LCM(A,B) =A*B
Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two
number.
510 and 92 510 and 92
Expressing 510 and 92 as product of its prime factors, we get,
510 = 2 × 3 × 17 × 5 × 1
92 = 2 × 2 × 23 × 1
Therefore, LCM(510, 92) = 2 × 2 × 3 × 5 × 17 × 23 = 23460
And HCF (510, 92) = 2
Verification
Now, product of 510 and 92 = 510 × 92 = 46920
And Product of LCM and HCF = 23460 × 2 = 46920
Hence, LCM × HCF = product of the 510 and 92.

13. • FIND LCM & HCF BY
APPLYING THE PRIME
FACTORISATION
METHOD
12,15,21
Writing the product of prime factors
for all the three numbers, we get,
12=2×2×3
15=5×3
21=7×3
Therefore,
HCF(12,15,21) = 3
LCM(12,15,21) = 2 × 2 × 3 × 5 × 7
= 420
• REVISITING IRRATIONAL NUMBER
RATIONAL NUMBER +IRRATIONAL NUMBER=REAL
NUMBER
A number is called Irrational if it cannot be written
in the form of p/q , where p and q are integers and
q ≠0
√2,√3,√15,Π,0.11011101111…….,

14. Theorem 1.3-Let p be a prime number ,if p divides
𝒂𝟐
,then p divides a,where a is a positive integars.
Solution
Let the prime factorisation of a be as below
a=𝒑𝟏𝒑𝟐𝒑𝟑𝒑𝟒 … … . . 𝒑𝒏 ,where 𝒑𝟏𝒑𝟐𝒑𝟑𝒑𝟒 … … . . 𝒑𝒏 are
primes ,not necessarily distinct.
therefore 𝒂𝟐
= (𝒑𝟏𝒑𝟐….𝒑𝒏 )(𝒑𝟏𝒑𝟐𝒑𝟑 … . 𝒑𝒏)=
𝒑𝟏
𝟐
𝒑𝟐
𝟐
……….𝒑𝒏
𝟐
Now we are given that p divides 𝒂𝟐,therefore from
the fundamental theorem of arithmetic , it follows
that p is one of the prime factors of 𝒂𝟐
How ever using the uniqueness part of the
fundamental theorem of arithmetic we realise that
the only prime factors of 𝒂𝟐
= 𝒑𝟏𝒑𝟐….𝒑𝒏 so is one
of the 𝒑𝟏,𝒑𝟐,𝒑𝟑, 𝒑𝟒 … … . . 𝒑𝒏
Now ,since a= 𝒑𝟏,𝒑𝟐,𝒑𝟑, 𝒑𝟒 … … . . 𝒑𝒏, p divides a
Hence proved

15. Prove that √5 is irrational.
Solutions: Let us assume, that √5 is rational number.
i.e. √5 = x/y (where, x and y are co-primes)
y√5= x
Squaring both the sides, we get,
(y√5)2 = x2
⇒5y2 = x2……………………………….. (1)
Thus, x2 is divisible by 5, so x is also divisible by 5.
Let us say, x = 5k, for some value of k and substituting the value of x in equation (1), we
get,
5y2 = (5k)2
⇒y2 = 5k2
is divisible by 5 it means y is divisible by 5.
Therefore, x and y are co-primes. Since, our assumption about is rational is incorrect.
Hence, √5 is irrational number.

19. *35/50
35/50 = 7/10,
Factorising the denominator, we get, 10 = 2×5
Since, the denominator is in the form of 2m × 5n thus, 35/50 has a terminating decimal
expansion.
*77/210
77/210 = (7× 11)/ (30 × 7) = 11/30
Factorising the denominator, we get, 30 = 2 × 3 × 5
As you can see, the denominator is not in the form of 2m × 5n .Hence, 77/210 has a non-
terminating decimal expansion.
*Is it rational or irrational
i)0.120120012000120000. . .
Since, it has non-terminating and non- repeating decimal expansion, it is an irrational
number.
ii) 43.123456789
Since it has non-terminating but repeating decimal expansion, it is a rational number in the
form of p/q and q has factors other than 2 and 5.

20. THANK YOU