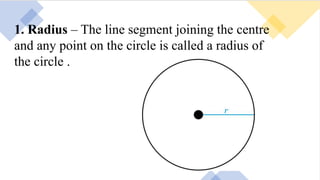
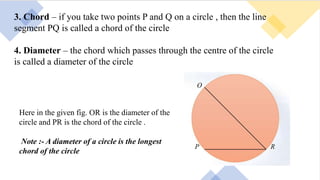
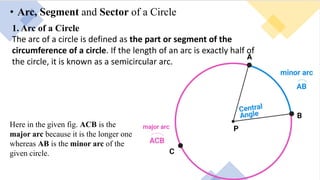
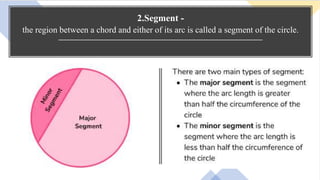
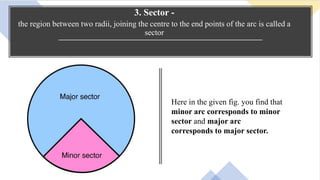
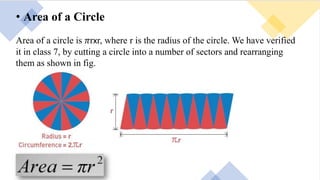
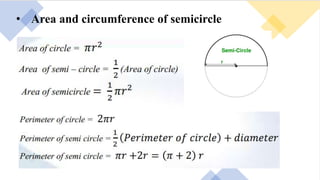
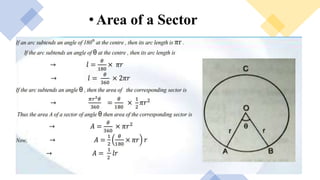
1. The document discusses various terms related to circles such as radius, diameter, chord, arc, segment, and sector. It defines each term and provides examples. 2. Formulas for calculating the circumference and area of a circle are presented. Circumference is defined as 2πr and area is defined as πr^2. 3. Methods for calculating the area of a sector and segment of a circle are described. The area of a sector is calculated based on the central angle and area of the whole circle. The area of a segment is not explicitly defined.

1. Mathematics
Art Integrated Activity

2. JAWAHAR
NAVODAYA
VIDYALAYA
KHEDGAON,
NASHIK
2022-23
Name- Swadesh Shivaji Jadhav
Class – 10
Div - 'A'
Roll no. - 1035/35
Sub - Mathematics
Guided By- A. D. Shinde sir

3. contents
Circle and its related terms .
Area of a circle .
Perimeter of a circle
Sector of a circle and its area .
Segment of a circle and its area
Areas of combinations of plane figures

4. • Circle and its related terms
Circle – Definition
The collection of all the points in a plane which are at
a fixed distance from in the plane is called a circle .
Or
A circle is a locus of a point which moves in a plane
in such a way that its distance from a fixed point
always remains same.

5. Terms Related to Circles

6. 1. Radius – The line segment joining the centre
and any point on the circle is called a radius of
the circle .

7. 2. A circle divides the plane on which it lies into
three parts .
They are
• The Interior of the circle .
• The circle . Exterior
• The exterior of the circle .
Here , in the given fig. We can see that point B is in the cricle, point A
is on the circle and point A is in exterior of the circle

8. 3. Chord – if you take two points P and Q on a circle , then the line
segment PQ is called a chord of the circle
4. Diameter – the chord which passes through the centre of the circle
is called a diameter of the circle
Here in the given fig. OR is the diameter of the
circle and PR is the chord of the circle .
Note :- A diameter of a circle is the longest
chord of the circle

9. • Arc, Segment and Sector of a Circle
1. Arc of a Circle
The arc of a circle is defined as the part or segment of the
circumference of a circle. If the length of an arc is exactly half of
the circle, it is known as a semicircular arc.
Here in the given fig. ACB is the
major arc because it is the longer one
whereas AB is the minor arc of the
given circle.

10. 2.Segment -
the region between a chord and either of its arc is called a segment of the circle.

11. 3. Sector -
the region between two radii, joining the centre to the end points of the arc is called a
sector
Here in the given fig. you find that
minor arc corresponds to minor
sector and major arc
corresponds to major sector.

12. • Circumference of a Circle
The perimeter of a circle is its boundary or the complete arc
length of the periphery of a circle.
We know that circumference of a circle bears a constant ratio with its
diameter .
Circumference = 2𝜋r

13. • Area of a Circle
Area of a circle is 𝜋rxr, where r is the radius of the circle. We have verified
it in class 7, by cutting a circle into a number of sectors and rearranging
them as shown in fig.

14. • Area and circumference of semicircle

15. • Area of a Sector
• Following are some important points to remember
• 1.A minor sector has an angle 𝜃, (say), subtended at the
centre of the circle , whereas a major sector has no angle .
• 2.The sum of arcs of major and minor sectors of a circle
is equal to the circumference of the circle.
• 3.The sum of the areas of major and minor sectors of a
circle is equal to the areas of the circle.
• 4.The boundary of a sector consists of an arc of the circle
and the two radii.

16. • Area of a Sector

17. Area of a segment of a circle