The document discusses various approaches to online quantile estimation, focusing on building data structures for efficient rank queries in streaming data. It highlights challenges in achieving exact answers while maintaining manageable storage requirements, leading to the development of approximate methods that provide tunable error bounds. Key techniques and algorithms are presented, including sketches and moment-based methods, which cater to high-cardinality scenarios and efficiency in merging large datasets.

1. Approaches to online quantile estimationApproaches to online quantile estimation
Joe Ross
Principal Data Scientist, Splunk
October 23, 2020
Data Con LA

4. The core problemThe core problem
Given a stream of numbers , build a data structure that can answer rank
queries, i.e.,
= number of stream elements
= some number such that , where is the current
stream length
Requirements:
Online operation: process the stream exactly once
Stream length not known in advance
Size of the data structure should have mild dependence on
Update (" ") and query operations should be fast
...

5. ApplicationsApplications
quantiles are fundamental summary statistics, especially for non-normal
distributions
time series anomaly detection
"observability" SLA monitoring: agree to serve 99.95% of requests within 50ms,
calculated per-month
"high cardinality" applications

6. First resultsFirst results
"Exact answers" and "mild dependence on " are incompatible
Munro-Paterson proved a lower bound for a -pass algorithm.
To answer queries exactly online ( ), need to store the whole stream.
White-box attack: given storage size , carefully designed size input leaves a problem as
hard as rank problem on input of size . Idea: always replace by indistinguishable
element, so next pass must compute on some set of size .
Formulate approximate versions: return rank/quantile within bounded error :
Then can also ask for tunability (required size as function of ).

7. Comments about theComments about the -approximate conditions-approximate conditions
Formulated in quantile space, not value space, i.e.,
the estimated 95th percentile is required to be between the actual 94th and 96th
percentiles;
~the estimated 95th percentile is required to be within 1% of the true 95th percentile~
formulation that makes sense for streams drawn for arbitrary ordered sets
invariant under monotonic transformations ("1%" guarantees are not preserved
under translation e.g.)
problem for guarantees in value space has several simple solutions (enhance xed
bins)
guarantees in quantile space can be arbitrarily bad in value space, and vice versa:
these are different problems
Now, imagine we could store the whole stream and then produce a compact read-only data
structure:

8. In [3]: ideal_samples()

9. Mergeability (another requirement)Mergeability (another requirement)
formed on separate streams
Mergeability means we can de ne a new data structure with similar error
guarantees as that of and (i.e., hard to distinguish from constructing on
).
Applications: distributed computing (separate machines), separate windows of time (or
other dimensions) to be re-assembled at query time

10. First approaches, continuedFirst approaches, continued
Munro-Paterson also provided algorithm that succeeds with high probability (for
nding median, say).
Maintain consecutive elements, counts and of elements below and above the -
element set.
View progression as random walk of ; will nd median if always .
Assuming equal probabilities, rst steps stay within of the origin (with high
probability).
( enables reduction to problem of size , hence favorable asymptotic size)

11. Greenwald-Khanna sketch maintains an ordered set of stream elements, together with
bounds on their possible ranks.
Denote by bounds on current rank of some stream element .
Sketch consists of:
Error for rank queries is bounded by
Insert an element by adding
Compression tries to merge tuples so that for all (the 's add under
merging consecutive elements)
Requires space

12. Essentially optimal solution: KLL sketch (careful sampling)Essentially optimal solution: KLL sketch (careful sampling)
A compactor holds items, each of weight ; can compact them into items each of
weight (keep even or odd elements, with equal probability).
Hierarchy of compactors of increasing size. Fix .
elements of weight
...
...
elements of weight
elements of weight

13. Express number of levels and compactions in terms of weights and stream size.
A single compaction produces error where and (whether even or
odd selected); sum over all compactions and levels, use Hoeffding's lemma.
Matches G-K size, simpli ed construction and arguments. Also mergeable.
Replace lower levels with samplers, keep constant in higher levels.
Optionally pass the whole device to G-K (loses mergeability); get , which is
optimal.

14. Relative errorRelative error
For skewed distributions (e.g., latency), care more about accuracy near the tails.
-digest prescribes desired accuracy as a function of quantile space
maintain sorted list of centroids: represents points near ; insertion and
merging mechanics
permissible centroid size governed by scale function (non-
decreasing)
cluster occupies in quantile space, then interval has
length (or cluster consists of one point)
ExamplesExamples

15. In [5]: scale_functions()

16. Non-linear scale function makes accuracy variable, error proportional to (something like)
for
Latency distributions have signi cant positive skew
Desire asymmetric accuracy: higher accuracy towards , lower towards
Property of the scale function that clusters satisfy condition after insertion/merging.

17. CharacterizationCharacterization
The scale function is decent ( accepts insertions for all ) if and only if
for all and all , we have:
for (moves to right) and
for (moves to left).
( is proportion occupied by inserted cluster)

18. In [7]: # Decent scale function must be continuous, in fact differentiable
discont()

19. Differentiability suggests tangent line construction to produce asymmetric -digest
In [9]: glued_scale_functions()
To verify decency, use one-variable characterization of decency:
and are non-increasing on

20. Errors and centroid counts for the usual ( rst row) and glued (second row) variants ofErrors and centroid counts for the usual ( rst row) and glued (second row) variants of
for for for

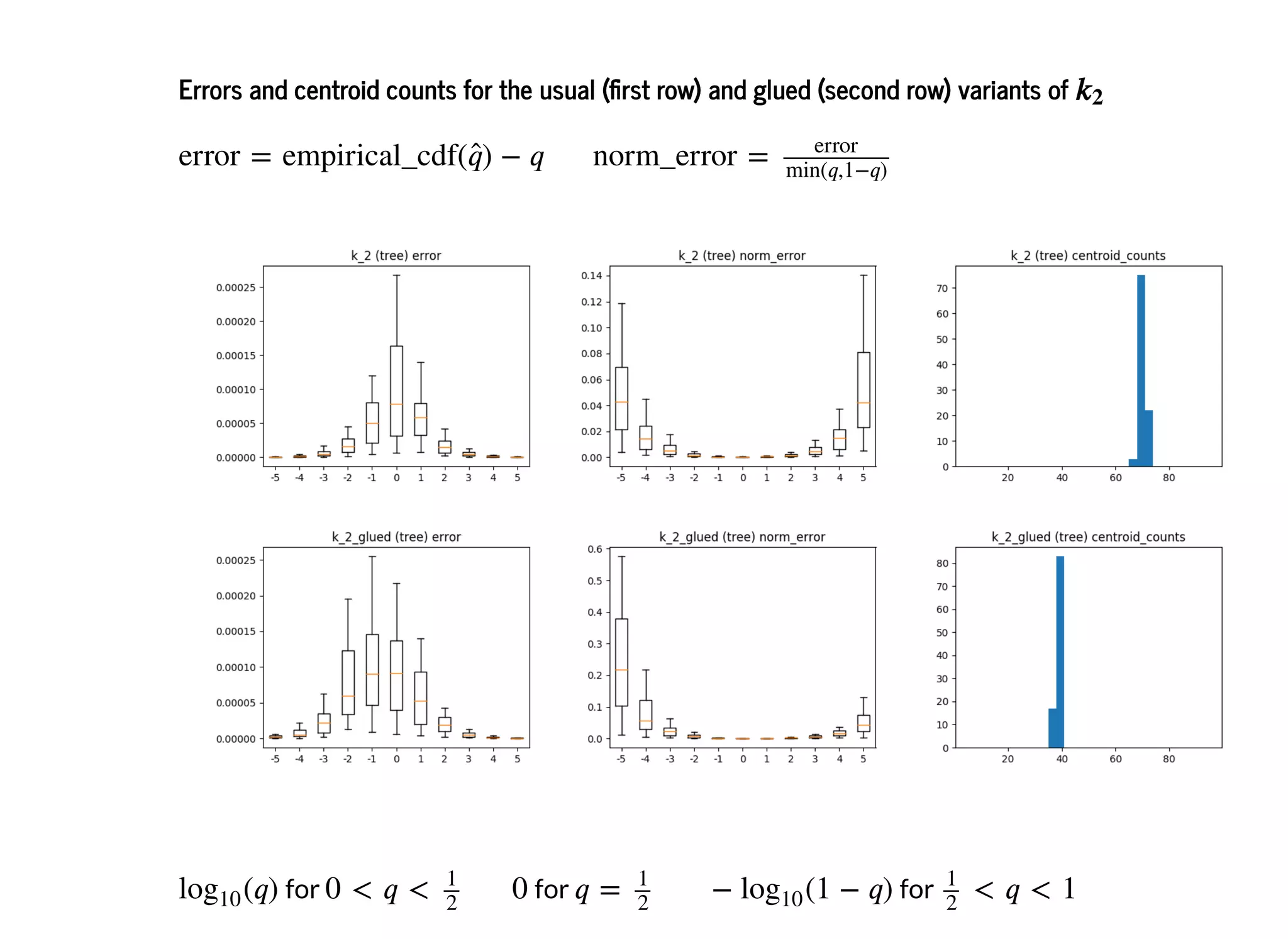
21. Relative error KLLRelative error KLL
Instead of ,
Corresponds to scale function.
Motivation: near , error is not so helpful.
Uses hierarchy of relative-compactors : only compact in the larger half, and "how close"
compaction gets to the median is controlled by an exponential distribution. (Vary sampling
across the distribution.)
Worse space than usual KLL (provably needed):
In a given level:
In [11]: relative_compactor()

22. Moment-based quantile sketchMoment-based quantile sketch
Motivation: why not just keep and use -score to answer rank/quantile queries?
Idea: sketch consists of several (log-)moments. Trivial to merge!
To extract quantiles: among all distributions realizing the empirical moments, pick one via
principle of maximum entropy and use its quantiles.
Solution from exponential family, ef cient numerical methods to solve optimization
problem.
In case two moments, amounts to assuming normal distribution.
Aimed at high-cardinality scenario in which answering a quantile query may require
merging millions of subsketches; for the sketches mentioned earlier, amounts to merging
millions of sorted lists. Addition of moments (even over millions of records) can be made
very fast because vectorizable.
Example: understand application performance across {user device type, geography,
software version, time}.

23. ReferencesReferences
J Ian Munro and Mike S Paterson. "Selection and sorting with limited storage." Theoretical
computer science, 12(3):315–323, 1980.
Michael Greenwald, Sanjeev Khanna, et al. "Space-ef cient online computation of quantile
summaries." ACM SIGMOD Record, 30(2):58–66, 2001.
Zohar Karnin, Kevin Lang, and Edo Liberty. "Optimal quantile approximation in streams." In
2016 IEEE 57th Annual Symposium on Foundations of Computer Science (FOCS), pages 71–78.
IEEE, 2016.
Ted Dunning, Otmar Ertl. "Computing extremely accurate quantiles using -digests."
arXiv:1902.04023, 2019.
Ted Dunning. "Conservation of the -digest scale invariant." arXiv:1903.09919, 2019.
Joe Ross. "Asymmetric scale functions for -digests." Submitted, 2019; branch of Dunning's
-digest repo.
Graham Cormode, Zohar Karnin, Edo Liberty, Justin Thaler, and Pavel Veselý. "Relative
error streaming quantiles." arXiv preprint arXiv:2004.01668, 2020.
Edward Gan, Jialin Ding, Kai Sheng Tai, Vatsal Sharan, Peter Bailis. "Moment-based quantile
sketches for ef cient high cardinality aggregation queries." Proceedings of the VLDB
Endowment, 11(11), 1647-1660, 2018.
https://github.com/signalfx/t-digest/tree/asymmetric/docs/asymmetric
(https://github.com/signalfx/t-digest/tree/asymmetric/docs/asymmetric)