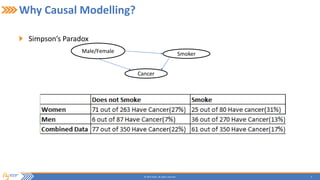
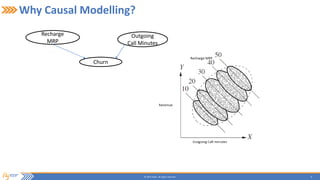
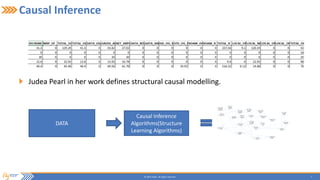
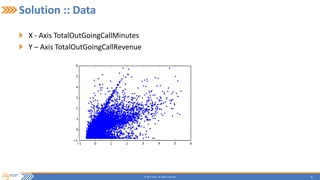
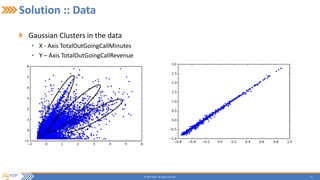
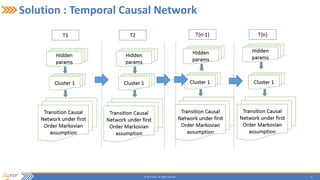
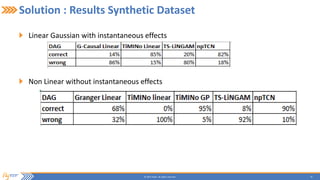
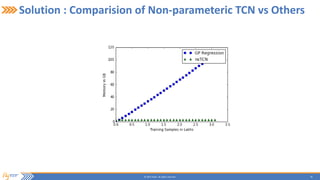
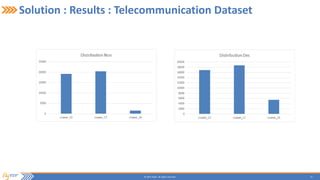
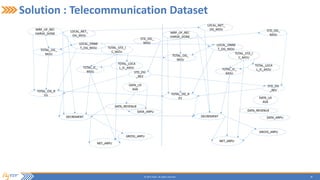
This document summarizes a presentation on incrementally learning non-stationary temporal causal networks from streaming telecommunication data. It introduces the problem of modeling causal relationships from large, non-stationary data. The solution presented combines Dirichlet process Gaussian mixture models with a Bayesian network structure learning algorithm to incrementally learn a non-parametric temporal causal network from streaming data. The algorithm detects concept drifts to trigger relearning. When applied to a real telecommunication dataset, it identified causal relationships and concept drifts without revisiting old data.