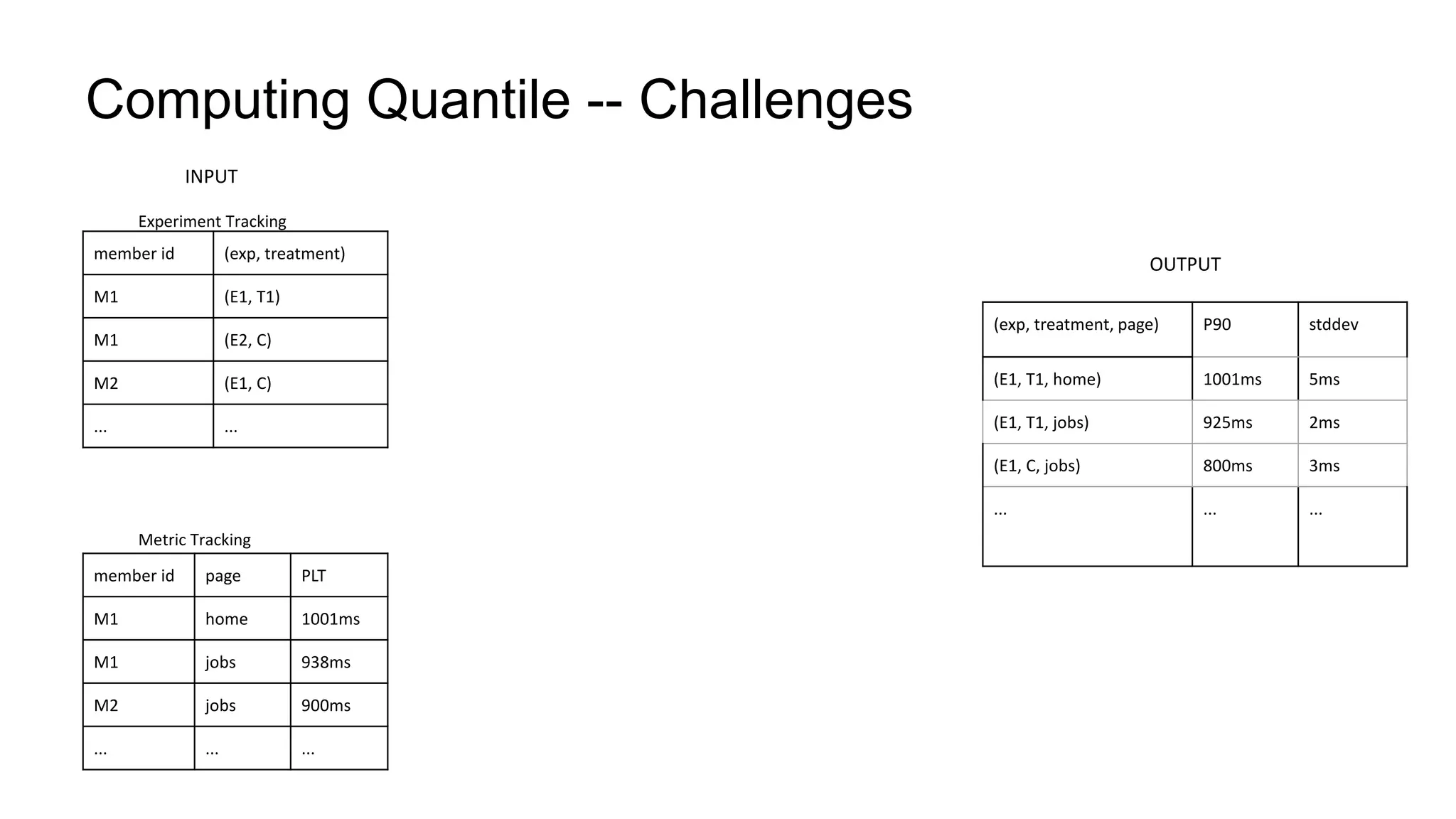
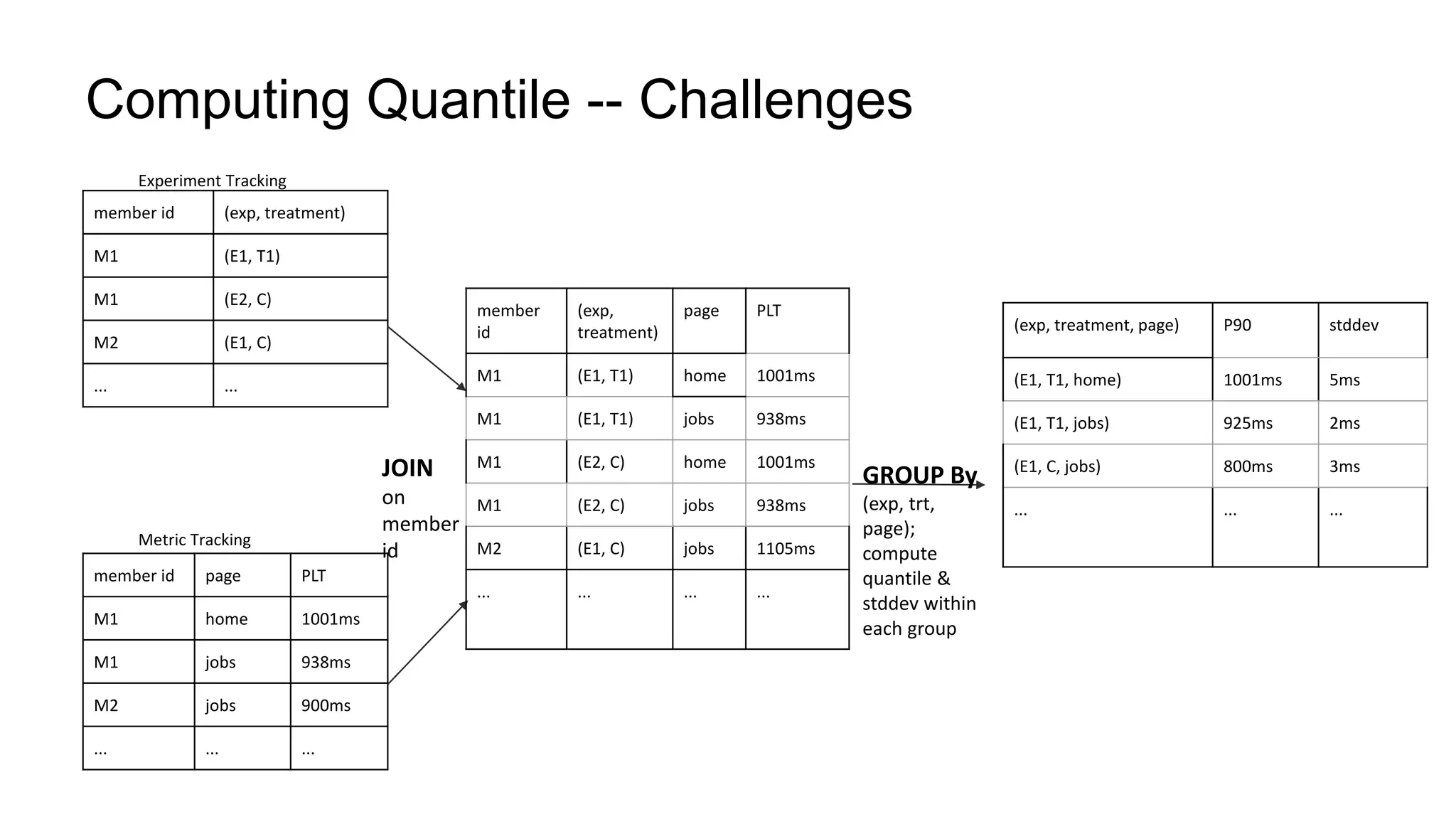
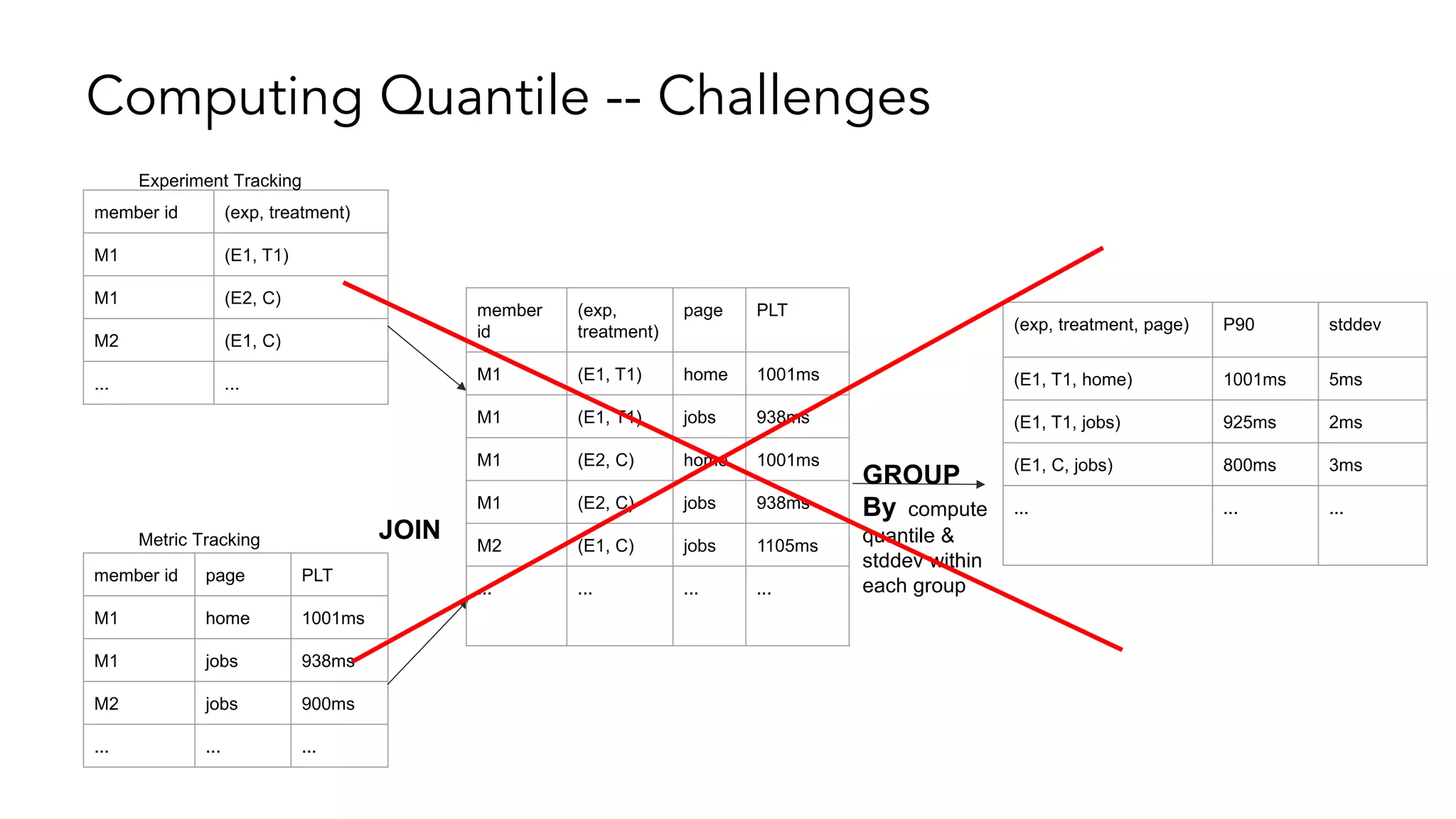
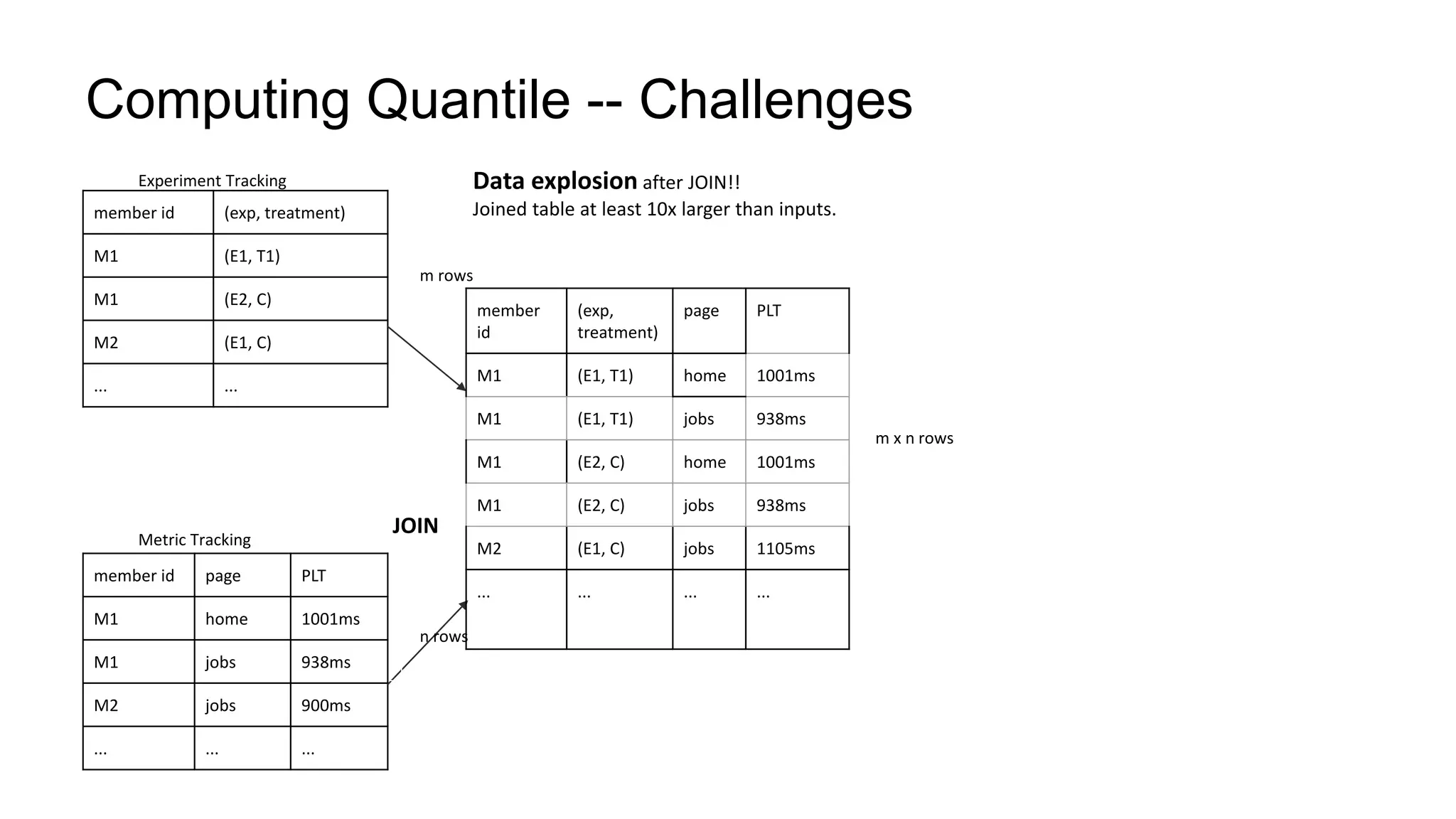
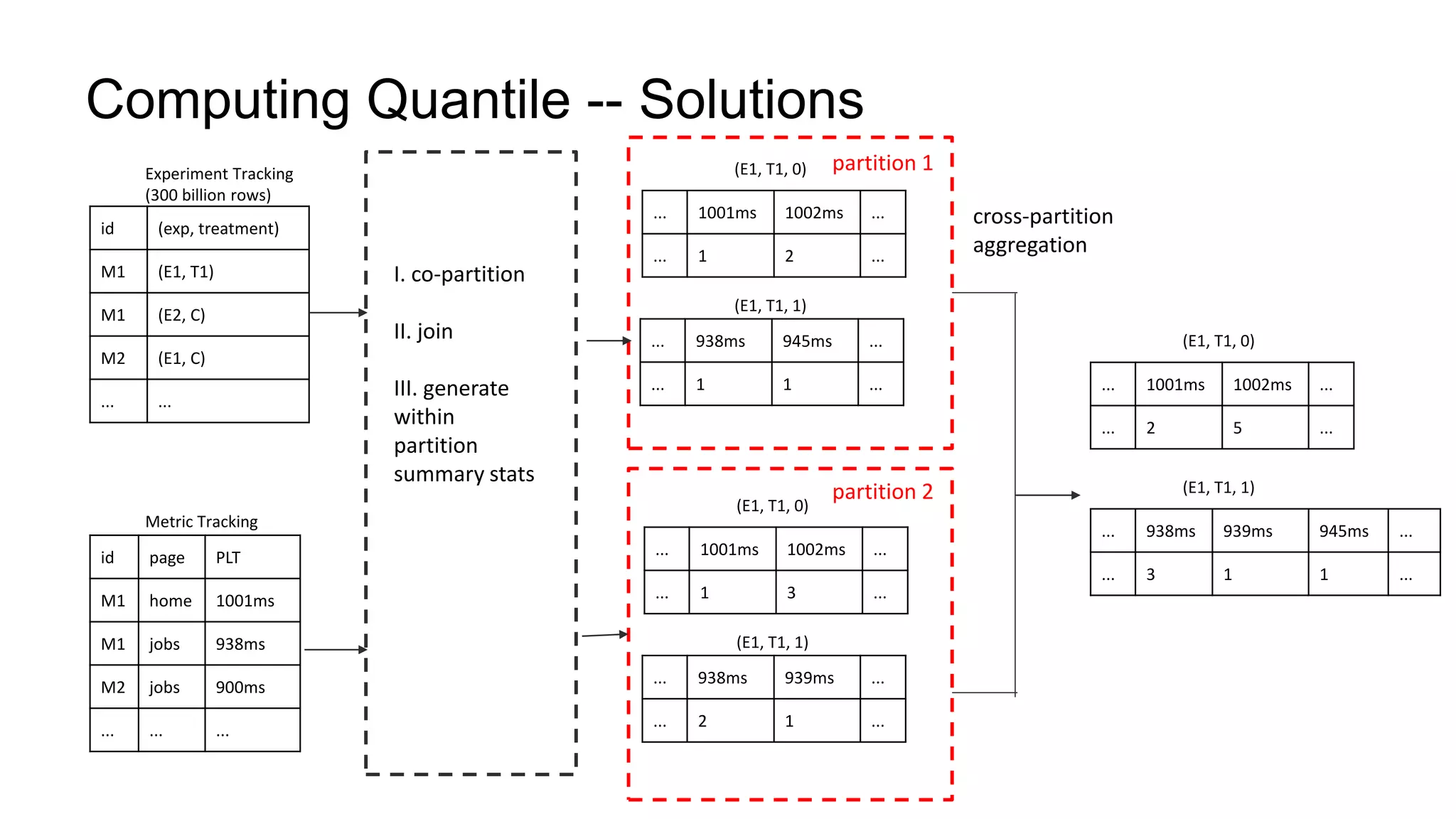
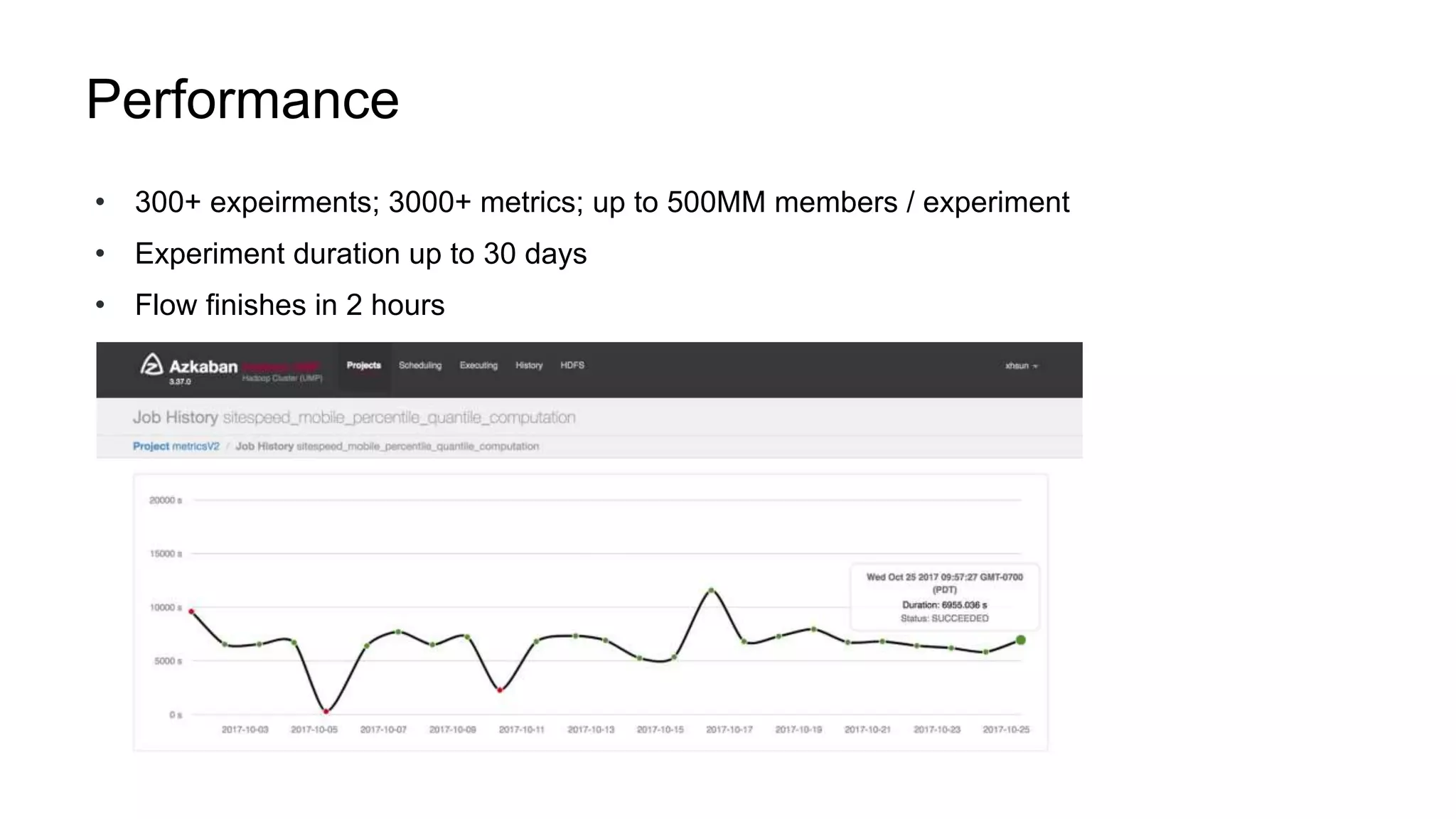
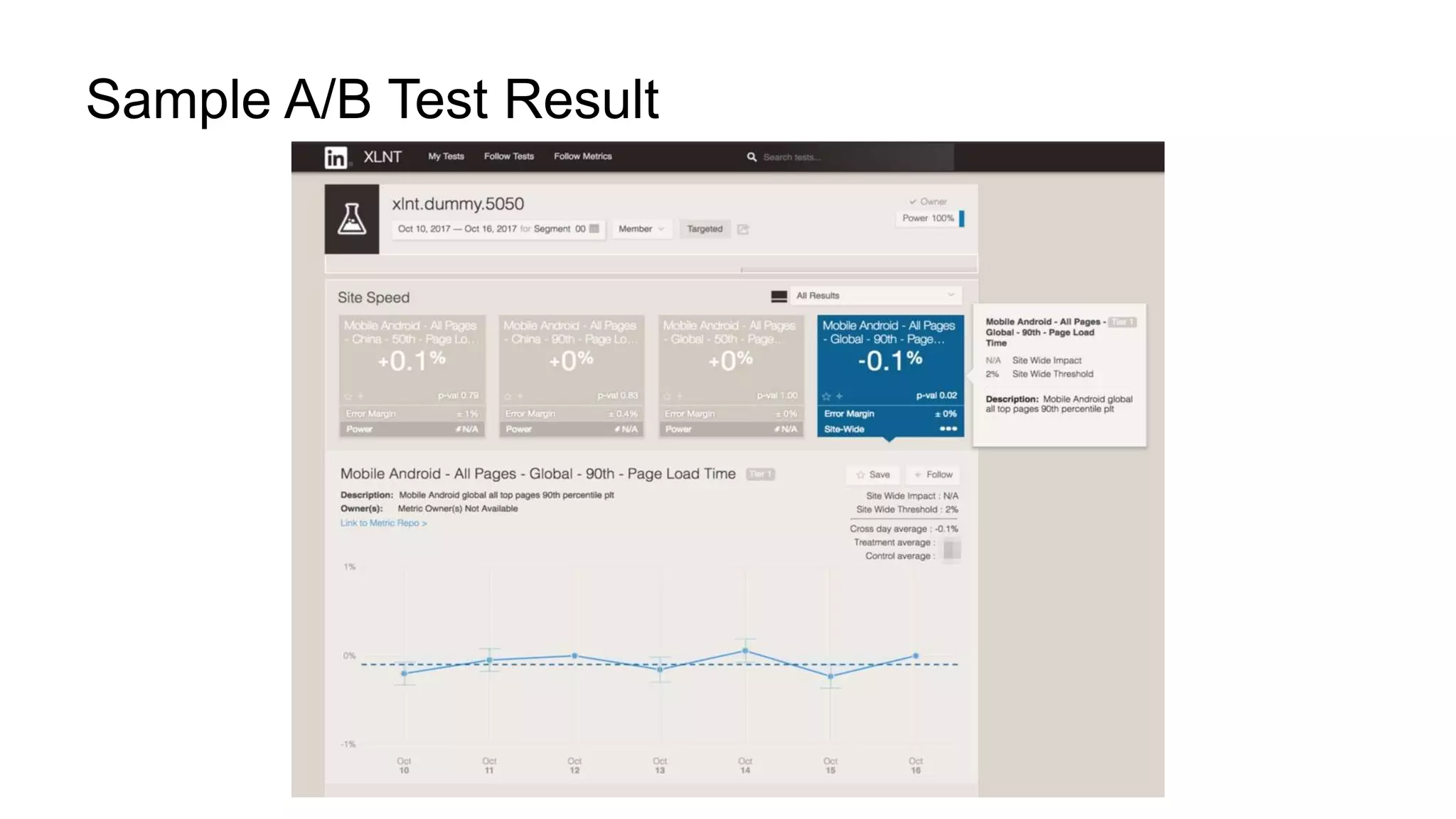
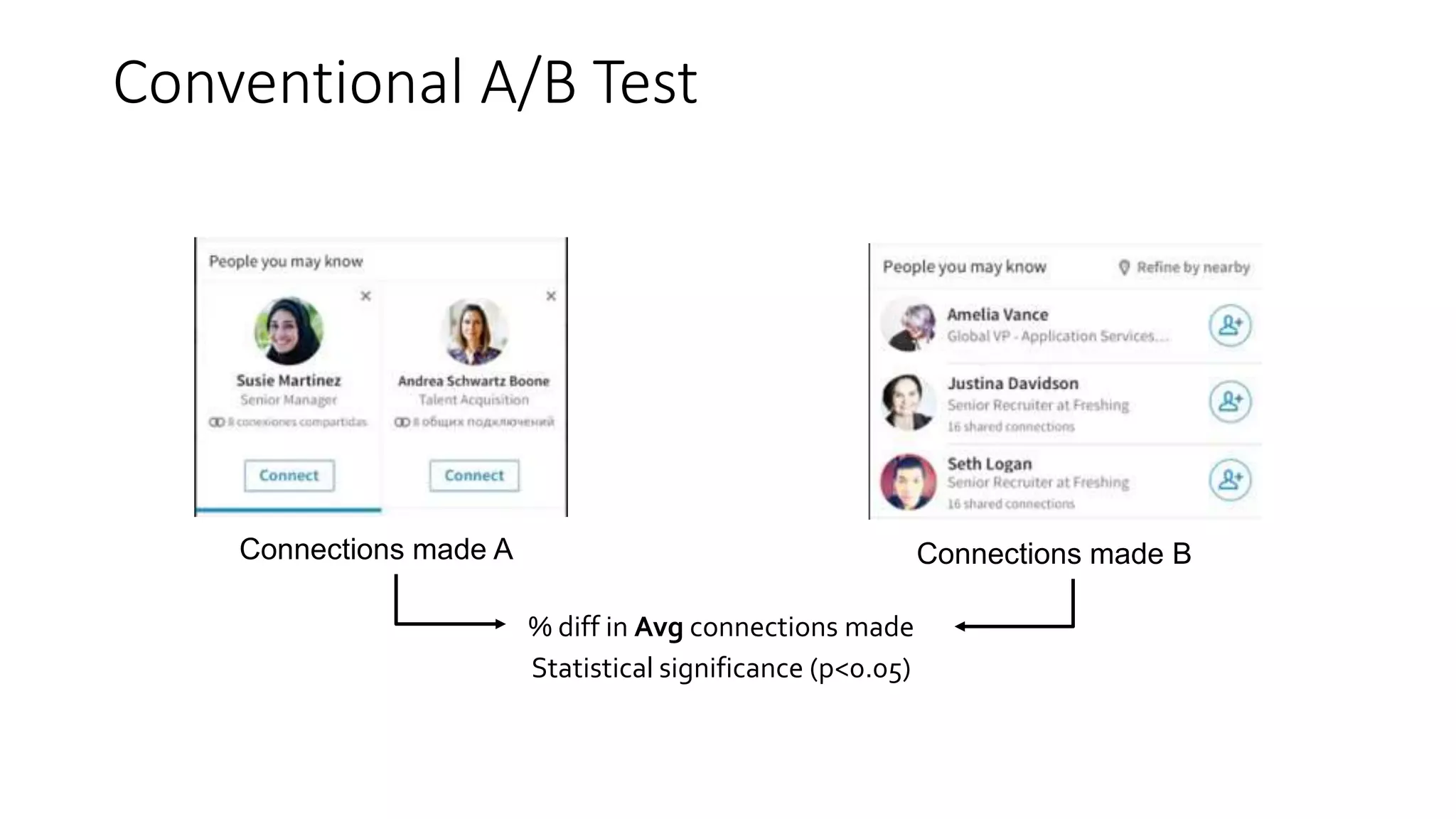
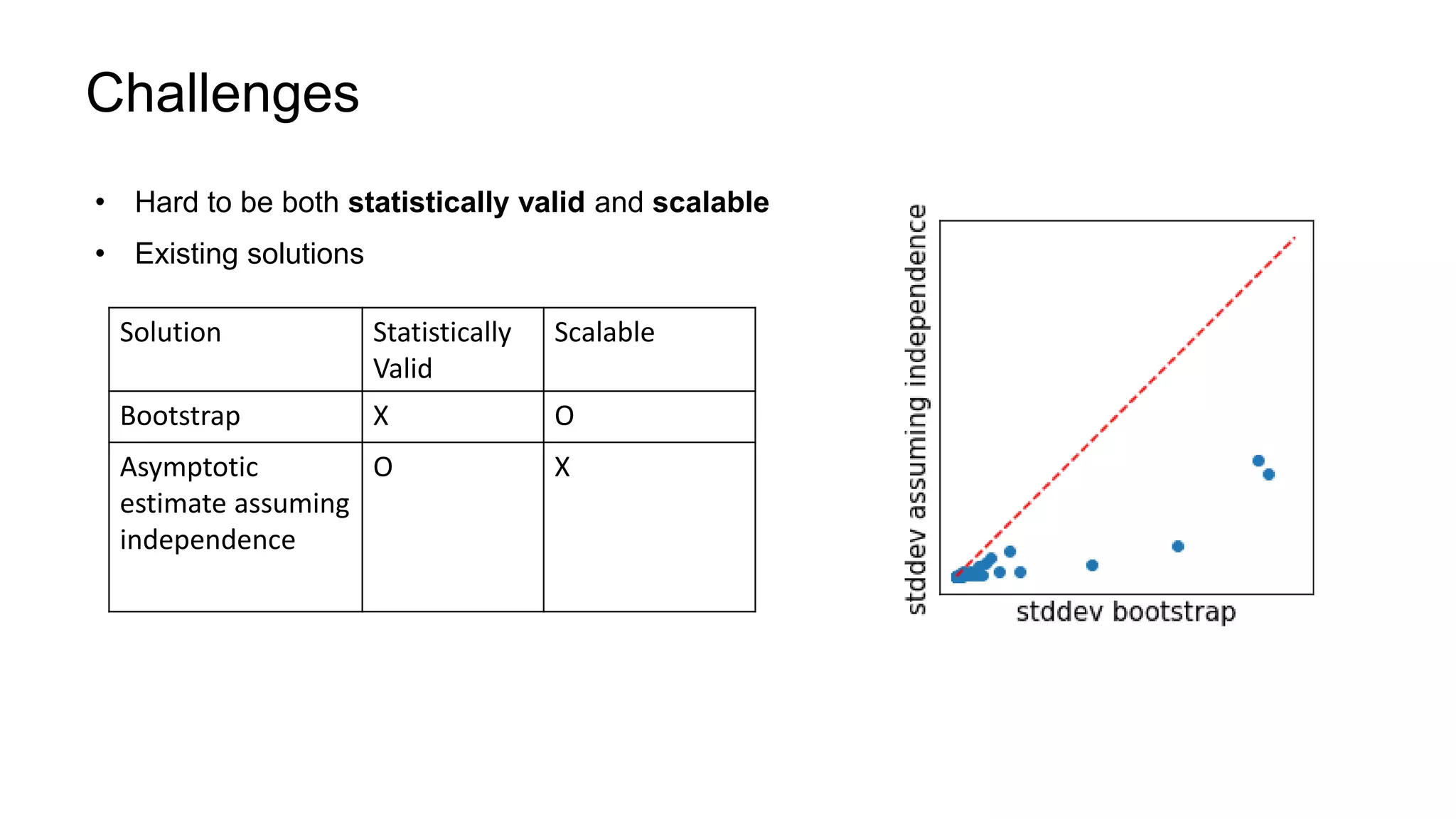
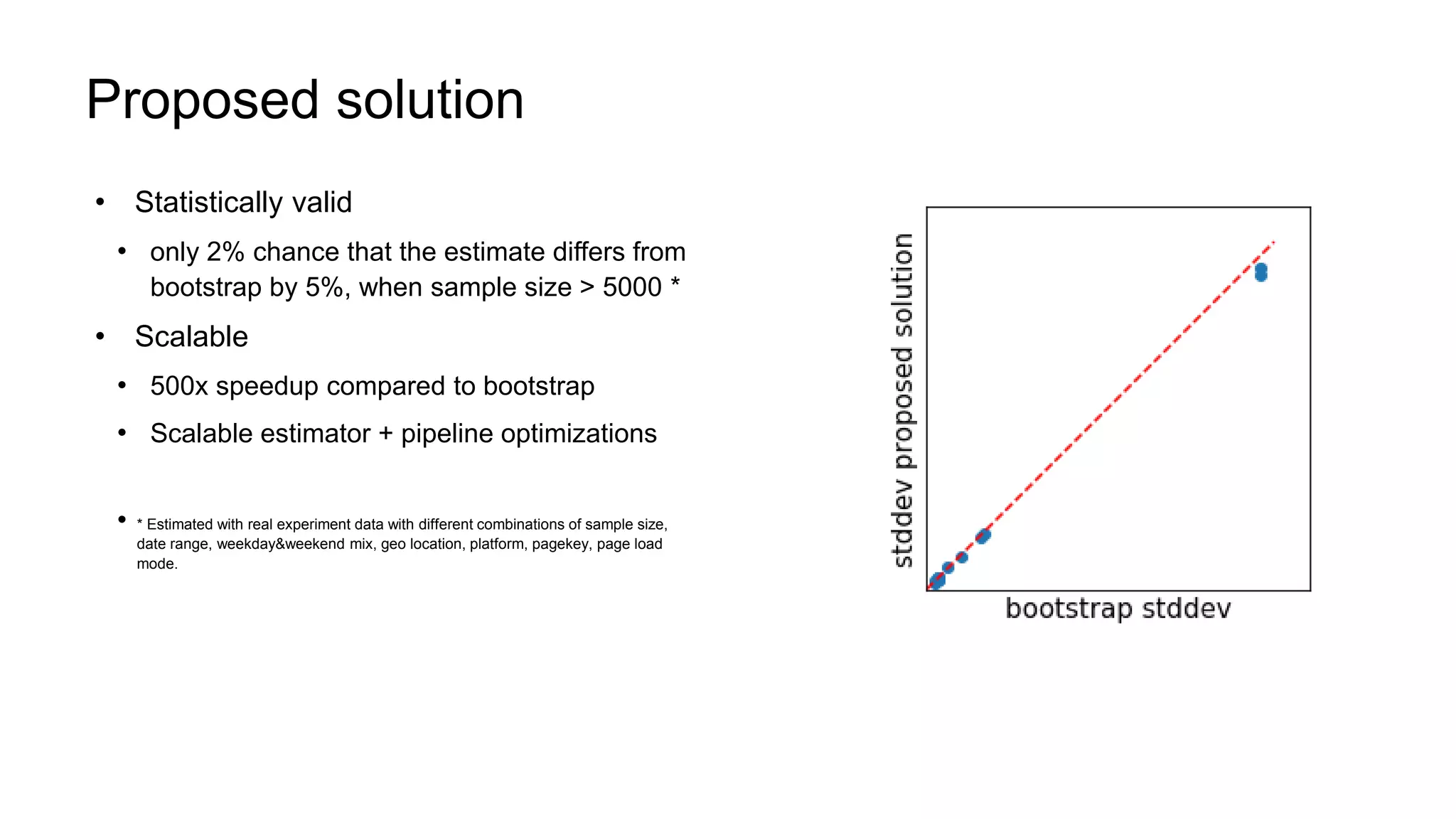
The document describes a methodology for conducting large-scale online experiments using quantile metrics. It outlines three key challenges: 1) ensuring experiments are statistically valid and scalable given hundreds of concurrent tests involving billions of data points, 2) existing solutions are either statistically valid or scalable but not both, and 3) protecting users from slow experiences by detecting degradation in page load time quantiles like P90. The proposed solution provides statistically valid quantile estimates while being 500x faster than traditional bootstrapping through an asymptotic distribution approximation, compressed data representations, and optimized pipeline design that involves co-partitioning and aggregating histogram summaries across partitions. Results demonstrated the ability to analyze over 300 experiments, 3000 metrics, and up to 500 million members

1. Large-Scale Online Experimentation with Quantile Metrics
Min Liu
Senior Applied Researcher, LinkedIn

2. Outline
• Motivation
• Challenges
• End-to-end solution
• Methodology for scalable and accurate estimate of quantile variance​
• Pipeline design​

3. Conventional A/B Test
A B
Connections made A Connections made B

4. Conventional A/B Test
A B
Connections made A Connections made B
% diff in Avg connections made
Statistical significance (p<0.05)

5. Why quantiles?
• Need to make sure slowest pages are not too slow
vs
All pages experience 0.5s
PLT increase
10% pages experience 5s
PLT increase
Same in average but different user perception

6. Why quantiles?
• Need to make sure slowest pages are not too slow
• Protect users from slow experience by detecting degradation in p90 PLT
vs
All pages experience 0.5s
PLT increase
10% pages experience 5s
PLT increase
Same in average but different user perception

7. Requirements for Quantile Metric A/B Testing
• Statistically valid
• Correct standard deviation, p-value, error margin
• Scalable
• 300+ concurrent A/B tests
• 500+ performance metric / experiment
• Up to 500 million members / experiment
• 300TB+
• Needs to finish 4hrs

8. Methodology

9. Challenges
• Hard to be both statistically valid and scalable
• Existing solutions
Solution Statistically
Valid
Scalable
Bootstrap X O
Asymptotic
estimate assuming
independence
O X

10. Proposed solution
• Statistically valid
• only 2% chance that the estimate differs from
bootstrap by 5%, when sample size > 5000 *
• Scalable
• 500x speedup compared to bootstrap
• Scalable estimator + pipeline optimizations
• * Estimated with real experiment data with different combinations of sample size,
date range, weekday&weekend mix, geo location, platform, pagekey, page load
mode.

11. Proposed solution
Members 𝑖 = 1,2, … , 𝑛
𝑖 has page views 𝑗 = 1,2, … , 𝑃𝑖
PLT of 𝑖 ‘s page view 𝑗 is 𝑋𝑖,𝑗
𝑄 -- sample quantile of
𝑋𝑖,𝑗’s
𝑠𝑡𝑑𝑑𝑒𝑣( 𝑄) -- standard
deviation of 𝑄
𝑛( 𝑄 − 𝑄)
𝐷
N(0, 𝜎2
)

12. Proposed solution
Members 𝑖 = 1,2, … , 𝑛
𝑖 has page views 𝑗 = 1,2, … , 𝑃𝑖
PLT of 𝑖 ‘s page view 𝑗 is 𝑋𝑖,𝑗
𝑄 -- sample quantile of
𝑋𝑖,𝑗’s
𝑠𝑡𝑑𝑑𝑒𝑣( 𝑄) -- standard
deviation of 𝑄
𝑛( 𝑄 − 𝑄)
𝐷
N(0, 𝜎2
)

13. Proposed solution
Members 𝑖 = 1,2, … , 𝑛
𝑖 has page views 𝑗 = 1,2, … , 𝑃𝑖
PLT of 𝑖 ‘s page view 𝑗 is 𝑋𝑖,𝑗
𝑄 -- sample quantile of
𝑋𝑖,𝑗’s
𝑠𝑡𝑑𝑑𝑒𝑣( 𝑄) -- standard
deviation of 𝑄
𝑛( 𝑄 − 𝑄)
𝐷
N(0, 𝜎2
)

14. Proposed solution
Asymptotic distribution with i.i.d PLT’s
⟺
Each member 𝑖 has 1 page view
𝐽𝑖 = 𝐼{𝑋𝑖 ≤ 𝑥}. 𝐽𝑖~𝐵𝑒𝑟𝑛 𝑝
𝐹𝑛(𝑥) =
1
𝑛 𝑖 𝐽𝑖.
1. 𝑛 𝐹𝑛 𝑄 − 𝐹 𝑄
𝐷
𝑁(0, 𝜎2
)
2. 𝑛 𝐹𝑛 𝑄 − 𝐹 𝑄
𝐷
𝑁(0, 𝜎2
)
3. 𝑛 𝑞 − 𝐹 𝑄
𝐷
𝑁(0, 𝜎2
)
4. 𝑛( 𝑄−𝑄)
𝐷
N(0,
𝜎2
𝑓 𝑄 2)
reference

15. Proposed solution
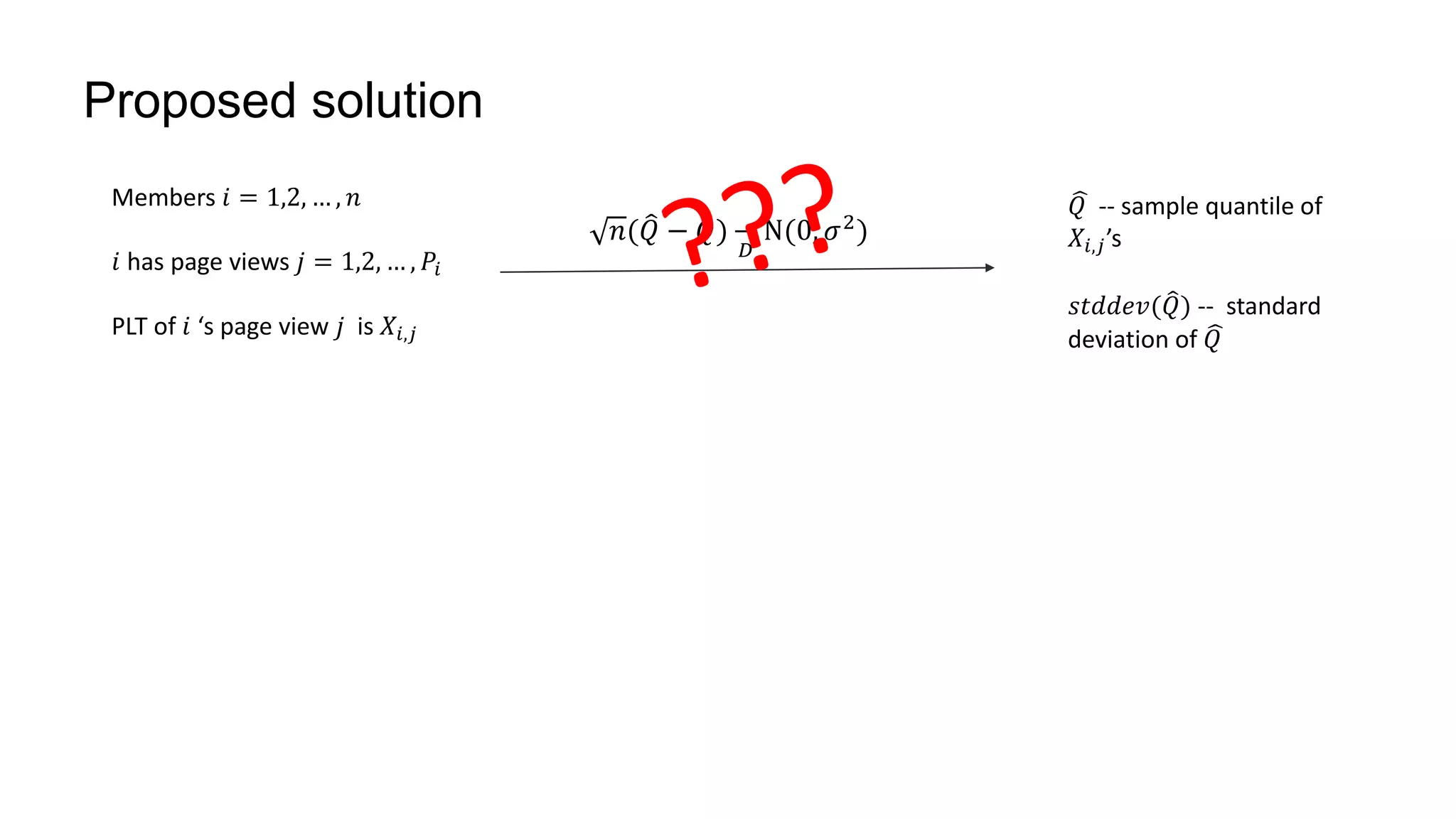
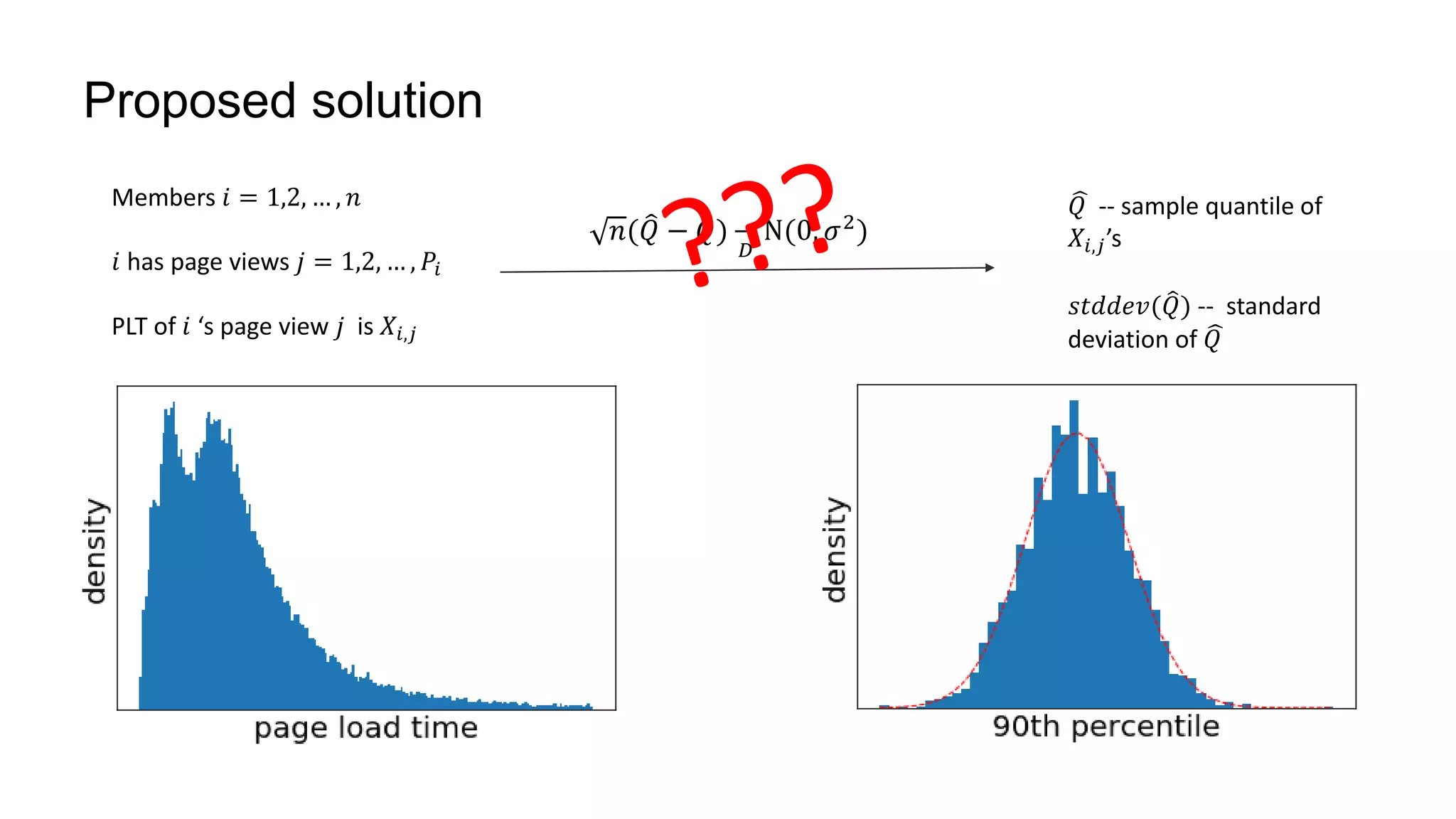
Asymptotic distribution with i.i.d PLT’s
⟺
Each member 𝑖 has 1 page view
𝐽𝑖 = 𝐼{𝑋𝑖 ≤ 𝑥}. 𝐽𝑖~𝐵𝑒𝑟𝑛 𝑝
𝐹𝑛(𝑥) =
1
𝑛 𝑖 𝐽𝑖.
1. 𝑛 𝐹𝑛 𝑄 − 𝐹 𝑄
𝐷
𝑁(0, 𝜎2
)
2. 𝑛 𝐹𝑛 𝑄 − 𝐹 𝑄
𝐷
𝑁(0, 𝜎2
)
3. 𝑛 𝑞 − 𝐹 𝑄
𝐷
𝑁(0, 𝜎2
)
4. 𝑛( 𝑄−𝑄)
𝐷
N(0,
𝜎2
𝑓 𝑄 2)
reference
Asymptotic distribution with non-i.i.d PLT’s
𝐽𝑖 = 𝑗 𝐼 𝑋𝑖,𝑗 ≤ 𝑥 . 𝐽𝑖’s are i.i.d
𝑌𝑛(𝑥) =
1
𝑛 𝑖 𝐽𝑖 and 𝑃𝑛 =
1
𝑛 𝑖 𝑃𝑖. 𝐹𝑛(𝑥) =
𝑌𝑛 𝑥
𝑃 𝑛
0. 𝑛[ 𝑌𝑛 𝑄
𝑃 𝑛
− 𝜇 𝐽
𝜇 𝑃
]
𝐷
𝑁(0, Σ)
1. 𝑛(𝐹𝑛(𝑄) − 𝐹(𝑄))
𝐷
𝑁(0, 𝜎 𝑃,𝐽
2
)
where 𝐹 𝑄 =
𝐹 𝑄 𝜇 𝑃
𝜇 𝑃
=
𝐸[𝐸(𝐽 𝑖|𝑃 𝑖)]
𝜇 𝑃
=
𝜇 𝐽
𝜇 𝑃
2. 𝑛 𝐹𝑛 𝑄 − 𝐹 𝑄
𝐷
𝑁(0, 𝜎 𝑃,𝐽
2
)
3. 𝑛 𝑞 − 𝐹 𝑄
𝐷
𝑁(0, 𝜎 𝑃,𝐽
2
)
4. 𝑛( 𝑄−𝑄)
𝐷
N(0,
𝜎 𝑃,𝐽
2
𝑓 𝑄 2)

16. Proposed solution – a few comments
• The derivation requires following conditions
• 𝐹𝑛 𝑥 does not have huge ‘steps’ and 𝑛step size 0 as 𝑛 ∞
• Sufficient condition is 𝑃𝑖 is bounded
• 𝑄 is a consistent estimate of 𝑄.
• True if 𝜇 𝑃 exists and is finite.

17. Proposed solution – a few comments
• 𝑓(𝑄) estimated by average density in a window ( 𝑄 − 𝛿, 𝑄 + 𝛿]
• 𝛿 set to 50ms for initial estimate
• Then set to 2 × 𝑠𝑡𝑑𝑑𝑒𝑣, turns out to be very effective in reducing estimation error

18. Pipeline Design

19. Computing Quantile -- Challenges
member id (exp, treatment)
M1 (E1, T1)
M1 (E2, C)
M2 (E1, C)
... ...
Experiment Tracking
Metric Tracking
member id page PLT
M1 home 1001ms
M1 jobs 938ms
M2 jobs 900ms
... ... ...
(exp, treatment, page) P90 stddev
(E1, T1, home) 1001ms 5ms
(E1, T1, jobs) 925ms 2ms
(E1, C, jobs) 800ms 3ms
... ... ...
INPUT
OUTPUT

20. Computing Quantile -- Challenges
member id (exp, treatment)
M1 (E1, T1)
M1 (E2, C)
M2 (E1, C)
... ...
Experiment Tracking
Metric Tracking
member id page PLT
M1 home 1001ms
M1 jobs 938ms
M2 jobs 900ms
... ... ...
member
id
(exp,
treatment)
page PLT
M1 (E1, T1) home 1001ms
M1 (E1, T1) jobs 938ms
M1 (E2, C) home 1001ms
M1 (E2, C) jobs 938ms
M2 (E1, C) jobs 1105ms
... ... ... ...
JOIN
on
member
id
GROUP By
(exp, trt,
page);
compute
quantile &
stddev within
each group
(exp, treatment, page) P90 stddev
(E1, T1, home) 1001ms 5ms
(E1, T1, jobs) 925ms 2ms
(E1, C, jobs) 800ms 3ms
... ... ...

21. Computing Quantile -- Challenges
member id (exp, treatment)
M1 (E1, T1)
M1 (E2, C)
M2 (E1, C)
... ...
Experiment Tracking
Metric Tracking
member id page PLT
M1 home 1001ms
M1 jobs 938ms
M2 jobs 900ms
... ... ...
member
id
(exp,
treatment)
page PLT
M1 (E1, T1) home 1001ms
M1 (E1, T1) jobs 938ms
M1 (E2, C) home 1001ms
M1 (E2, C) jobs 938ms
M2 (E1, C) jobs 1105ms
... ... ... ...
JOIN
GROUP By
compute
quantile &
stddev within
each group
(exp, treatment, page) P90 stddev
(E1, T1, home) 1001ms 5ms
(E1, T1, jobs) 925ms 2ms
(E1, C, jobs) 800ms 3ms
... ... ...

22. Computing Quantile -- Challenges
member id (exp, treatment)
M1 (E1, T1)
M1 (E2, C)
M2 (E1, C)
... ...
Experiment Tracking
Metric Tracking
member id page PLT
M1 home 1001ms
M1 jobs 938ms
M2 jobs 900ms
... ... ...
member
id
(exp,
treatment)
page PLT
M1 (E1, T1) home 1001ms
M1 (E1, T1) jobs 938ms
M1 (E2, C) home 1001ms
M1 (E2, C) jobs 938ms
M2 (E1, C) jobs 1105ms
... ... ... ...
JOIN
Data explosion after JOIN!!
Joined table at least 10x larger than inputs.
m rows
n rows
m x n rows

23. Computing Quantile -- Solutions
• Compress input
• Experiment tracking → Bitmap; compression rate 30x
• Encode string with numbers; e.g. 0 = home, 1 = jobs
• Be smarter about join
• Co-partition both inputs by member id.
• Store PLT’s under each (exp, treatment, page) as a histogram
• Aggregate histograms across partitions

24. Computing Quantile -- Solutions
id (exp, treatment)
M1 (E1, T1)
M1 (E2, C)
M2 (E1, C)
... ...
Experiment Tracking
(300 billion rows)
Metric Tracking
id page PLT
M1 home 1001ms
M1 jobs 938ms
M2 jobs 900ms
... ... ...
(E1, T1, 0)
... 1001ms 1002ms ...
... 1 2 ...
(E1, T1, 1)
... 938ms 945ms ...
... 1 1 ...
...
partition 1
I. co-partition
II. join
III. generate
within
partition
summary stats
(E1, T1, 0)
... 1001ms 1002ms ...
... 1 3 ...
(E1, T1, 1)
... 938ms 939ms ...
... 2 1 ...
...
partition 2
(E1, T1, 0)
... 1001ms 1002ms ...
... 2 5 ...
(E1, T1, 1)
... 938ms 939ms 945ms ...
... 3 1 1 ...
...
cross-partition
aggregation

25. Computing Stddev of Quantile
• Almost the same as computing quantiles, except summary stats are different
• Instead of histogram, we now compute within partition
• 𝐽 = 𝑖 𝐽𝑖 = 𝑖,𝑗 𝐼 𝑋𝑖,𝑗 ≤ 𝑄 --# of pageviews with plt ≤ quantile 𝑄
• 𝑃 = 𝑖 𝑃𝑖 --# of total pageviews
• 𝐽2
= 𝑖 𝐽𝑖
2
-- cross product of 𝐽 and 𝑃 for computing variance-covariance matrix Σ
• 𝑃2
= 𝑖 𝑃𝑖
2
-- cross product of 𝐽 and 𝑃 for computing variance-covariance matrix Σ
• 𝐽𝑃 = 𝑖 𝐽𝑖 𝑃𝑖 -- cross product of 𝐽 and 𝑃 for computing variance-covariance matrix Σ
• 𝑛 -- # of unique members
• 𝐷 = 𝑖,𝑗 𝐼 𝑄 − 𝛿 ≤ 𝑋𝑖,𝑗 ≤ 𝑄 + 𝛿 --# of pageviews within a window around 𝑄, to estimate 𝑓(𝑄)
• Cross-partition aggregation is simply taking sum
• Stddev adjustment is the same as the stddev computation, except changing the window to 2
× 𝑠𝑡𝑑𝑑𝑒𝑣

26. Results

27. Performance
• 300+ expeirments; 3000+ metrics; up to 500MM members / experiment
• Experiment duration up to 30 days
• Flow finishes in 2 hours

28. Sample A/B Test Result