Embed presentation
Download as PDF, PPTX

![4
Variational Models
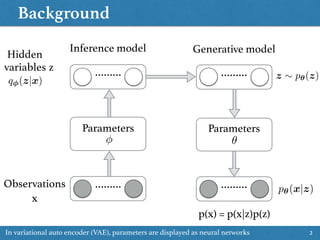
• We want to compute posterior p(z|x) (z: latent variables, x: data)
• Variational inference seeks to minimize
for a family q(z; )
KL(q(z; )||p(z|x))
• Maximizing evidence lower bound (ELBO)
log p(x) Eq(z; )[log p(x|z)] KL(q(z; )||p(z))
• (Common) Mean-field distribution q(z; ) =
Y
i
q(zi; i)
• Hierarchical variational models
• (Newer) Interpret the family as a variational model for posterior
latent variables z (introducing new latent variables)[1]
Lawrence, N. (2000). Variational Inference in Probabilistic Models. PhD thesis.](https://image.slidesharecdn.com/01020160216variationalgaussianprocess-160216094213/85/010_20160216_Variational-Gaussian-Process-4-320.jpg)



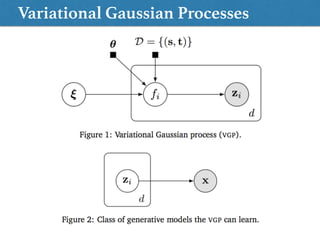










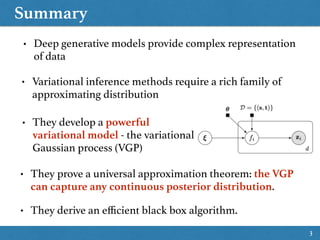
The document discusses the development of the Variational Gaussian Process (VGP) as a powerful variational model capable of capturing any continuous posterior distribution, proven through a universal approximation theorem. It highlights the use of deep generative models and variational inference methods to effectively represent complex data. Additionally, an efficient black box algorithm for VGP is introduced within the context of hierarchical variational models.



![4
Variational Models
• We want to compute posterior p(z|x) (z: latent variables, x: data)
• Variational inference seeks to minimize
for a family q(z; )
KL(q(z; )||p(z|x))
• Maximizing evidence lower bound (ELBO)
log p(x) Eq(z; )[log p(x|z)] KL(q(z; )||p(z))
• (Common) Mean-field distribution q(z; ) =
Y
i
q(zi; i)
• Hierarchical variational models
• (Newer) Interpret the family as a variational model for posterior
latent variables z (introducing new latent variables)[1]
Lawrence, N. (2000). Variational Inference in Probabilistic Models. PhD thesis.](https://image.slidesharecdn.com/01020160216variationalgaussianprocess-160216094213/85/010_20160216_Variational-Gaussian-Process-4-320.jpg)












