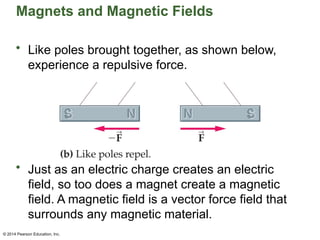
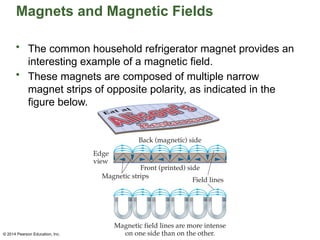
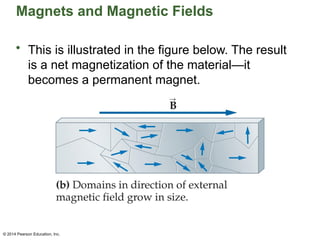
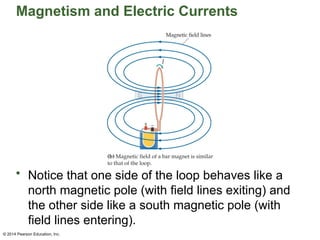
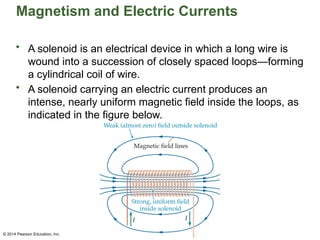
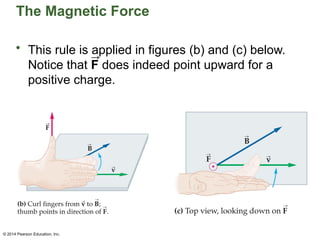
Chapter 22 discusses magnetism, magnetic fields, and the connection between electricity and magnetism, highlighting the basic properties of magnets, such as poles and their interactions. It explains how electric currents create magnetic fields and introduces the concept of solenoids as electromagnets. Additionally, the chapter covers Earth's magnetic field, its historical reversals, and the principles governing magnetic fields generated by current-carrying wires.