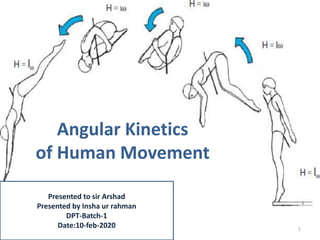
Angular Kinetics of Human Movement discusses angular analogues to linear motion concepts. [1] Moment of inertia is the angular equivalent to mass, representing resistance to angular acceleration based on an object's mass distribution from the axis of rotation. [2] During human movement like walking, the leg's moment of inertia depends on the knee angle, changing the mass distribution. [3] Angular momentum is the product of moment of inertia and angular velocity, remaining constant in the absence of external torque like linear momentum.

1. Angular Kinetics
of Human Movement
Presented to sir Arshad
Presented by Insha ur rahman
DPT-Batch-1
Date:10-feb-2020 1

2. Angular analogue of Mass
• Angular analogue of mass is inertia , mass is a body’s inertial characteristic
for considerations relative to linear motion.
• According to Newton’s second law, the greater a body’s mass, the greater
its resistance to linear acceleration.
• Within the human body, the distribution of mass with respect to an axis of
rotation can dramatically influence the relative ease or difficulty of moving
the body limbs. For example, during gait, the distribution of a given leg’s
mass, and therefore its moment of inertia with respect to the primary axis
of rotation at the hip, depends largely on the angle present at the knee.
2

3. Resistance to Angular Acceleration
• Movement of inertia:
• The inertial property for rotating bodies represent the resistance to
angular acceleration , based on both the mass and the distance.
• The mass is distributed from the axis of rotation.
• Movement of inertia is the sum of product of each particle’s
mass(m) and radius of rotation (r) for that particle square , so we
get the equation
• I=E(sum of)mr2
3

4. • Radius of Gyration:
• Distance from axis of rotation to a point where body mass is
become concentrated without altering its rotational
characteristics.
• Used to calculated the mass distribution for calculating the
movement of inertia , by ,
• I=mk2
• Since knee angle effect the movement of inertia in a swinging
leg respect to the hip because of changes in the radius of
gyration for the lower leg (k2) and foot (k3)
4

5. • Angular analogue of momentum:
• The quantity of angular motion passessed by the measured
as the product of moment of inertia and angular velocity.
• For linear motion: M=mv
• For angular motion: H=Iw(angular velocity)
• Or: H=mk2w
5

6. • Principle of conversion of Angular
momentum:
• The total angular momentum of given system remains
constant in the absence of external torque mean’s
• (initial momentum)H1=H2(Final momentum)
• When the angular momentum is conserved then there is a
trade off between movement of inertia(i) and angular
velocity.(w)
• Like in above picture in tuck position= Small(i) & large(w)
• Extended position=large (i) & small (w) 6

7. • What produces change in angular
momentum?
• Angular impulse – the product of torque and the time interval
over which the torque acts:
• Tt = change(delta) in momentum
• Tt= (iw)2- (iw)1
7

8. Angular analogues of linear quantities
8

9. ANGULAR ANALOGUES OF NEWTON’S LAWS
OF MOTION:
• Newton’s First Law:
• The angular version of the fi rst law of motion may be stated
as follows
• “A rotating body will maintain a state of constant rotational
motion unless acted on by an external torque.”
• In the analysis of human movement in which mass remains
constant .
• Throughout, this angular analogue forms the underlying basis
for the principle of conservation of angular momentum.
9

10. • Newton’s Second Law:
• In angular terms, Newton’s second law may be stated
algebraically and in words as the following:
• T=I@(alpha)
• A net torque produces angular acceleration of a body that is
directly proportional to the magnitude of the torque, in the
same direction as the torque, and inversely proportional to
the body’s moment of inertia
• In accordance with Newton’s second law for angular motion,
the angular acceleration of the fore-arm is directly
proportional to the magnitude of the net torque at the elbow
and in the direction (flexion) of the net torque at the elbow.
• The greater the moment of inertia is with respect to the axis
of rotation at the elbow, the smaller is the resulting angular
acceleration
10

11. • Newton’s Third Law:
• The law of reaction may be stated in angular form as the following:
• “For every torque exerted by one body on another, there is an equal and
opposite torque exerted by the second body on the first”.
• When a baseball player forcefully swings a bat, rotating the mass of the
upper body, a torque is created around the player’s longitudinal axis.
• The batter’s feet are not firmly planted, the lower body tends to rotate
around the longitudinal axis in the opposite direction.
• However, since the feet usually are planted, the torque generated by the
upper body is translated to the ground, where the earth generates a
torque of equal magnitude and opposite direction on the cleats of the
batter’s shoes.
11

12. CENTRIPETAL FORCE:
• Force directed toward the center of rotation for a body in rotational
motion is known as centripetal force.
• When an object attached to a line is whirled around in a circular path and
then released, the object flies off on a path that forms a tangent to the
circular path it was following at the point at which it was released, since
this is the direction it was traveling in at the point of release.
• Centripetal force prevents the rotating body from leaving its circular path
while rotation occurs around a fixed axis.
12

13. • It can be formulated as ,
• Centripetal force may also be defined in terms of angular
velocity:
13

14. • Some examples:
• (1):Twirling a lasso, spinning a ball on a string(Like a Bola): Centripetal
Force is provided by the force of tension on the rope pulls the object in
toward the center.
• (2):Turning a car: Centripetal Force is provided by the force of Friction
between the wheels and the ground.
• (3)Riding a Gravitron, going through a loop on a roller coaster. Centripetal
Force is provided by the Normal Force as the wall or seat pushes you
toward the center.
• (4):The Earth orbiting around the Sun: Centripetal Force is provided by the
Force of Gravity.
14

15. 15