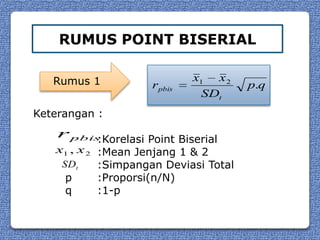
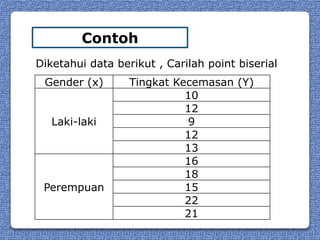
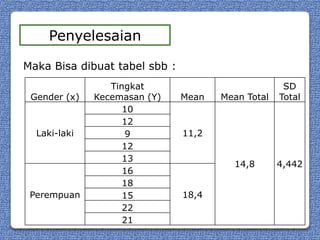
Dokumen tersebut memberikan penjelasan tentang point biserial, yaitu korelasi yang digunakan untuk satu variabel diukur dalam skala interval atau rasio dan variabel lainnya adalah variabel nominal dengan dua tingkatan klasifikasi. Diberikan rumus untuk menghitung point biserial beserta contoh perhitungannya menggunakan data gender dan tingkat kecemasan. Point biserial kemudian diinterpretasikan dengan membandingkannya terhadap nilai r tabel.

1. KORELASI POINT BISERIAL

2. Definisi
Point Biserial adalah korelasi yang
digunakan untuk satu variabel diukur dalam
skala interval atau rasio dan variabel lainnya
adalah variabel nominal dengan dua
tingkatan klasifikasi (variabel dikotomi)

3. Hal Yang Harus Diperhatikan Dalam
Point Biserial
Data nominal (kategori) yang digunakan harus
murni nominal, bukan data hasil transformasi dari
tipe data lain. Misal, umur pada awalnya bertipe
rasio, namun setelah ditransformasi bisa menjadi
data kategorik.
Contoh:
umur 010= kecil, 1017 = remaja, 1725= dewasa,
dst...
Tipe data ini tidak diperkenankan untuk digunakan
dalam korelasi point biserial.

4. RUMUS POINT BISERIAL
Rumus 1 x1 x 2
rpbis p.q
SDt
Keterangan :
r pbis:Korelasi Point Biserial
x1 , x 2 :Mean Jenjang 1 & 2
SDt :Simpangan Deviasi Total
p :Proporsi(n/N)
q :1-p

5. RUMUS POINT BISERIAL
x1 xt p
Rumus 2 rpbis
SDt q
Keterangan :
r pbis
:Korelasi Point Biserial
x1 :Mean Jenjang1
x t :Mean Total
SDt :Simpangan Deviasi Total
p :Proporsi (n/N)
q :1-p

6. Contoh
Diketahui data berikut , Carilah point biserial
Gender (x) Tingkat Kecemasan (Y)
10
12
Laki-laki 9
12
13
16
18
Perempuan 15
22
21

7. Penyelesaian
Dimisalkan x1=Laki-laki ; x2=Perempuan
x1i 10 12 9 12 13
x1 11,2
n1 5
x2 i 16 18 15 22 21
x2 18,4
n2 5
x1 x2 11,2 18,4
Mean total 14,8
2 2
(x x) 2 177,6
SDtotal 19,733 4,442
n 1 9

8. Penyelesaian
Maka Bisa dibuat tabel sbb :
Tingkat SD
Gender (x) Kecemasan (Y) Mean Mean Total Total
10
12
Laki-laki 9 11,2
12
13
14,8 4,442
16
18
Perempuan 15 18,4
22
21

9. Penyelesaian
x1 11,2 x2 18,4 xt 14 ,8 SDt 4,442
p (n/N) 5/10 0,5 q 1 p 1 0,5 0,5
x1 x2
Rumus 1
r pbis p.q
SDt
11,2 18,4
rpbis 0,5 0,5
4,42
rpbis 1,6281 0,5
rpbis 8,144

10. Penyelesaian
Rumus 2 x1 xt p
rpbis
SDt q
11,2 14,8 0,5
rpbis
4,442 0,5
rpbis 0,8144 1
rpbis 0,8144

11. Interpretasi point Biserial
Untuk menguji hipotesa nihil, koefisien point
biserial harus dibandingkan dengan r tabel
Untuk melihat r tabel harus dicari df=N-2
•rpbis ≥ rtabel = H0Ditolak
•rpbis < rtabel = H0Diterima