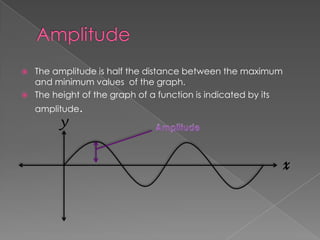
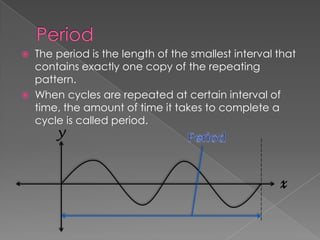
The document defines amplitude and period for sine, cosine, tangent, cotangent, secant, and cosecant functions. Amplitude is the maximum value of the function and period is the interval over which the function repeats. Formulas are provided to calculate amplitude and period based on the function: amplitude is the absolute value of the coefficient and period depends on the coefficient in front of x. Several examples are worked out applying the formulas. Exercises at the end have the reader determine the amplitude and period for additional functions.

1. AMPLITUDE &
PERIOD

3. 

The amplitude is half the distance between the maximum
and minimum values of the graph.
The height of the graph of a function is indicated by its
amplitude.
y
x

4. 

The period is the length of the smallest interval that
contains exactly one copy of the repeating
pattern.
When cycles are repeated at certain interval of
time, the amount of time it takes to complete a
cycle is called period.
y
x

6. To get the period of a sine function of the form y= a
sin bx or f(x)= a sin bx
amplitude (a) = |a|
period (p) = |2π/b|
Example 1:
Determine the amplitude and period of y=sin x
amplitude (a) = |a|
period (p) =
|2π/b|
= |1|
=
|2π/1|
=1
= 2π

7. Example 2:
Determine the amplitude and period of y= -2 sin 2x
amplitude (a) = |a|
= |-2|
=2
period (p) = |2π/b|
= |2π/2|
=π
Example 3:
Determine the amplitude and period of y= 3 sin ½ x
amplitude (a) = |a|
= |3|
=3
period (p) = |2π/b|
= |2π/ ½ |
=4 π

8. To get the amplitude and period of a sine function of the form y=
a cos bx or f(x)= a cos bx
amplitude (a) = |a|
period (p) = |2π/b|
Example 1:
Determine the amplitude and period of y=cos x
amplitude (a) = |a|
= |1|
=1
period (p) = |2π/b|
= |2π/ 1|
=2π

9. Example 2:
Determine the amplitude and period of y= 5 cos ¼ x
amplitude (a) = |a|
= |5|
=5
period (p) = |2π/b|
= |2π/ ¼ |
= 8π
Example 3:
Determine the amplitude and period of y= -3 cos ½ x
amplitude (a) = |a|
= |-3|
=3
period (p) = |2π/b|
= |2π/ ½ |
=4 π

10. To get the period of tangent function of the form y= a tan
bx or f(x)= a tan bx
period (p) = |π/b|
Example 1:
Determine the period of y= tanx
period (p) = |π/b|
= |π/1|
=π

11. Example 2:
Determine the period of y= 8 tan 2x
period (p) = |π/b|
= |π/2|
= π/2
Example 3:
Determine the period of y=2 tan ¼ x
period (p) = |π/ b|
= |π/ ¼ |
= π/4

12. Tangent and cotangent are called reciprocal functions. This implies
that the period of cotangent is also π just like tangent. This also means
that they have the same way of getting their period.
period (p) = |π/b|
Example 1:
Determine the period of y= cot x
period (p) = |π/b|
= |π/1|
=π

13. The cosecant and secant functions are reciprocal of sine and cosine
functions, respectively. This means that their periods are also 2π.
The graph of cosecant function is related to sine graph in the same
way the graph of secant function is related to the cosine graph.
Example 1:
Determine the amplitude and period of y= csc x
Get the amplitude and period corresponding sine function, y = sin x
amplitude (a) = |a|
= |1|
=1
period (p) = |2π/b|
= |2π/1|
= 2π

14. Example 1:
Determine the amplitude and period of y= sec x
Get the amplitude and period corresponding cosine function, y =
cos x
amplitude (a) = |a|
= |1|
|2π/1|
=1
period (p) = |2π/b|
=
= 2π

16. Determine the amplitude and period of each of
the following.
Amplitude
Period
1. y= sin 3x
_______
______
2. y= cos 2x
_______
______
3. y= -6 cos 2/3 x
_______
______
4. y= 4/3 sin ¼ x
_______
______
5. y= 8 cos πx
_______
______

17. Give the period of each of the following.
Period
y= 4 sec 3x
2. y= -2 csc 1/5 x
3. y= -6 tan 2/3 x
4. y= cot ¼ x
5. y= tan 2πx
1.
__________
__________
__________
__________
__________

19. 
1.
2.
3.
4.
5.
Exercise 1
amplitude
period
1
1
6
4/3
8

1.
2.
2π/3
π
3π
8π
2
3.
4.
5.
Exercise 2
π/3
5π
3 π/2
4π
½