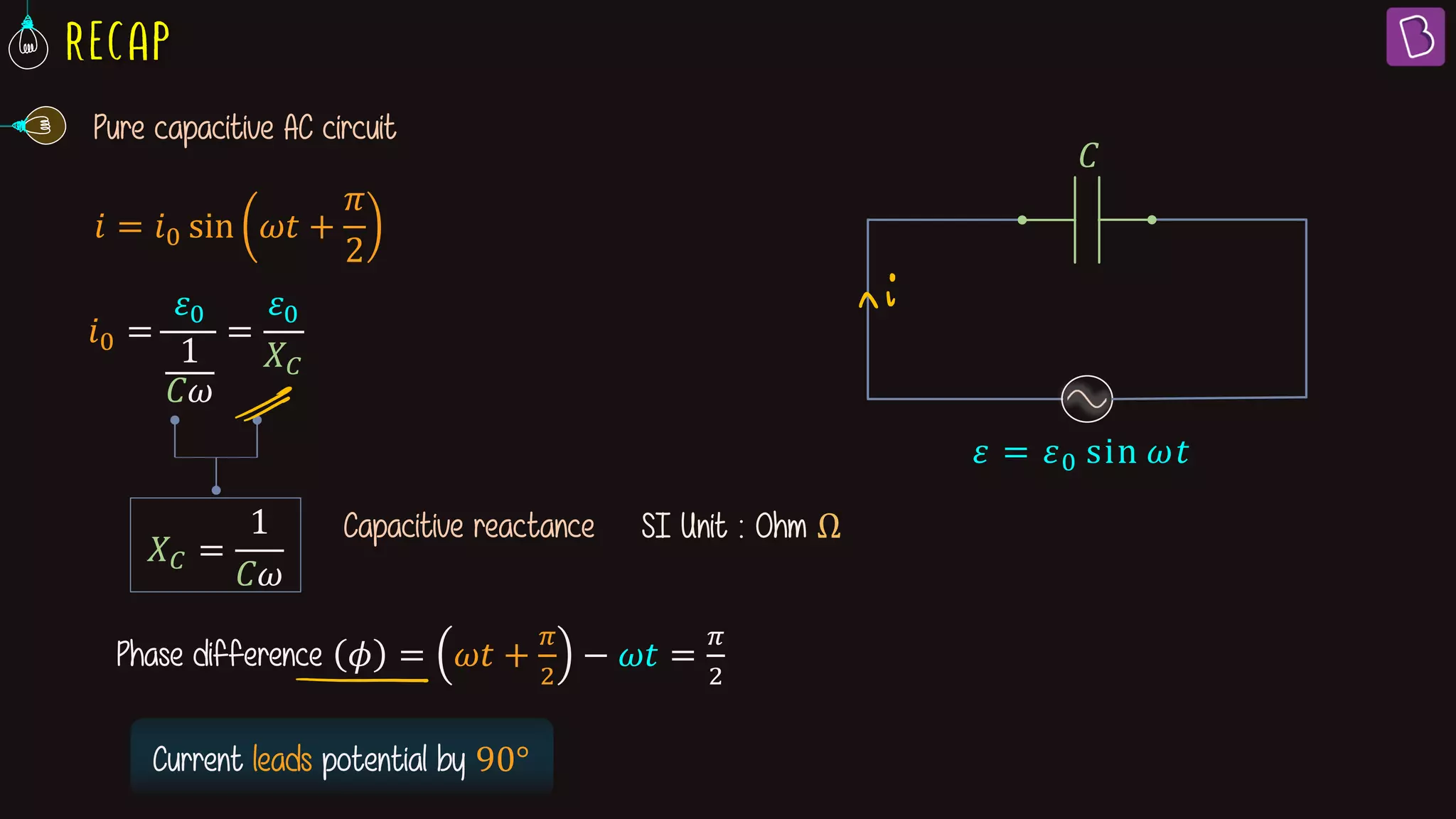
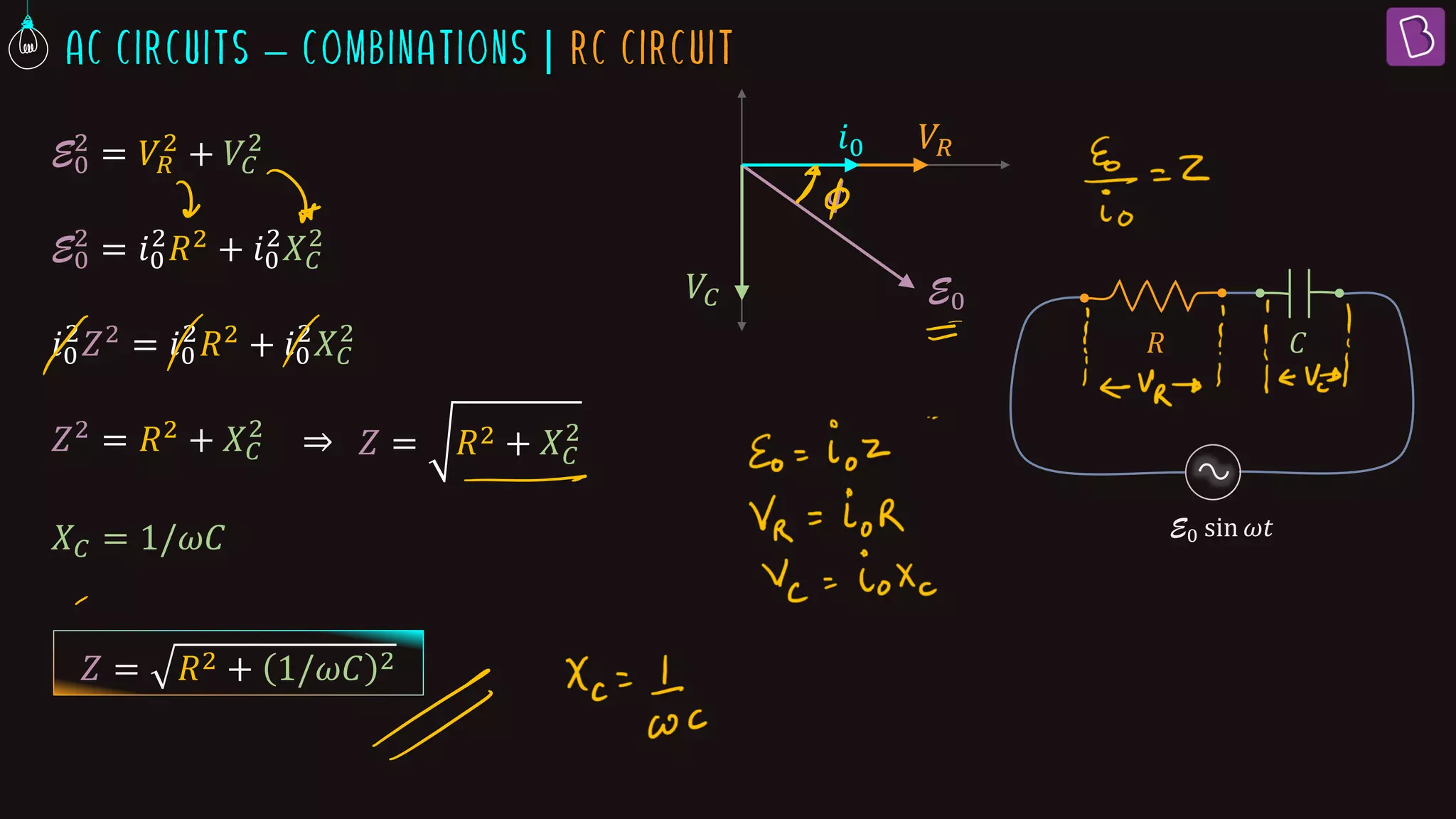
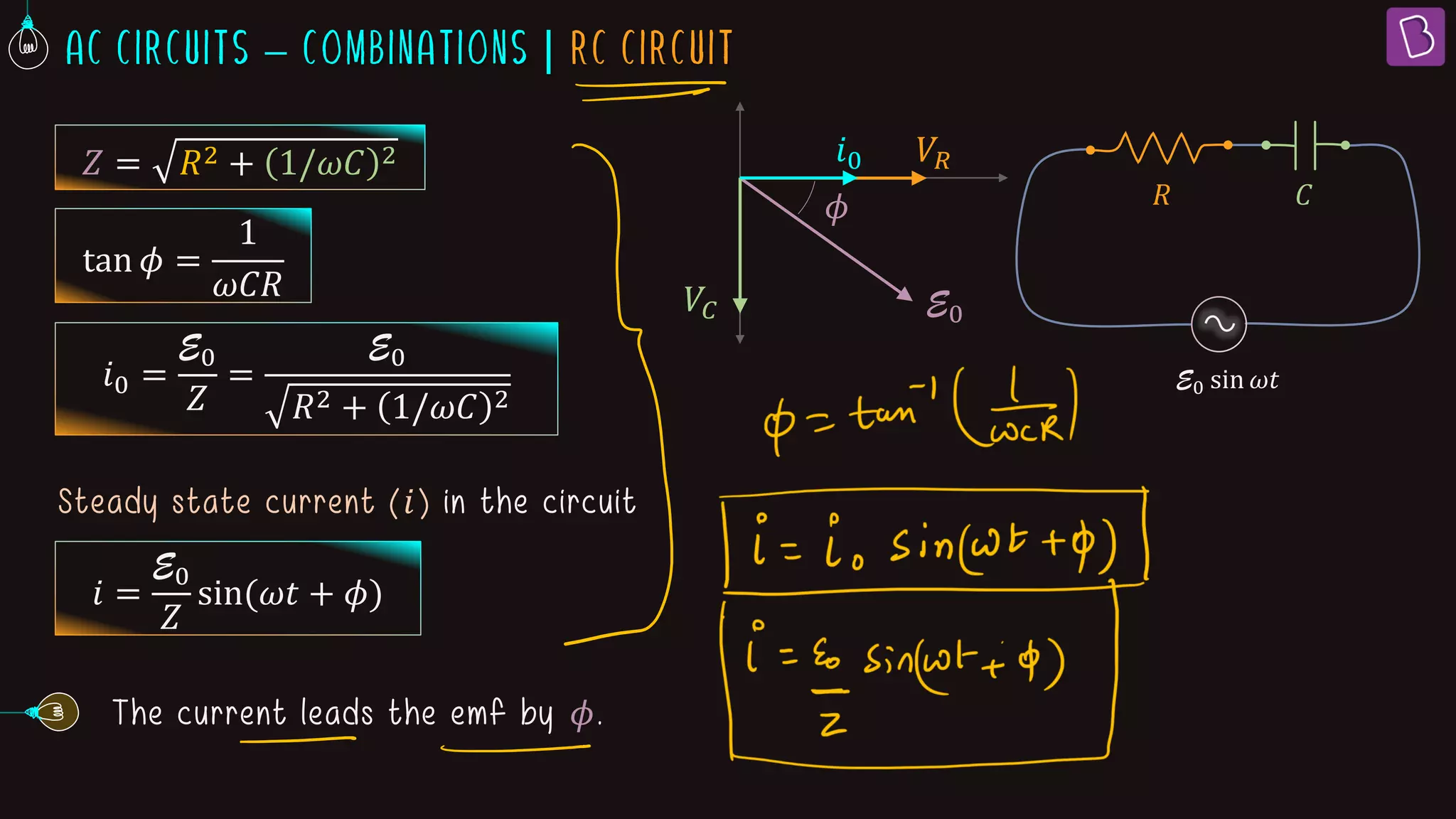
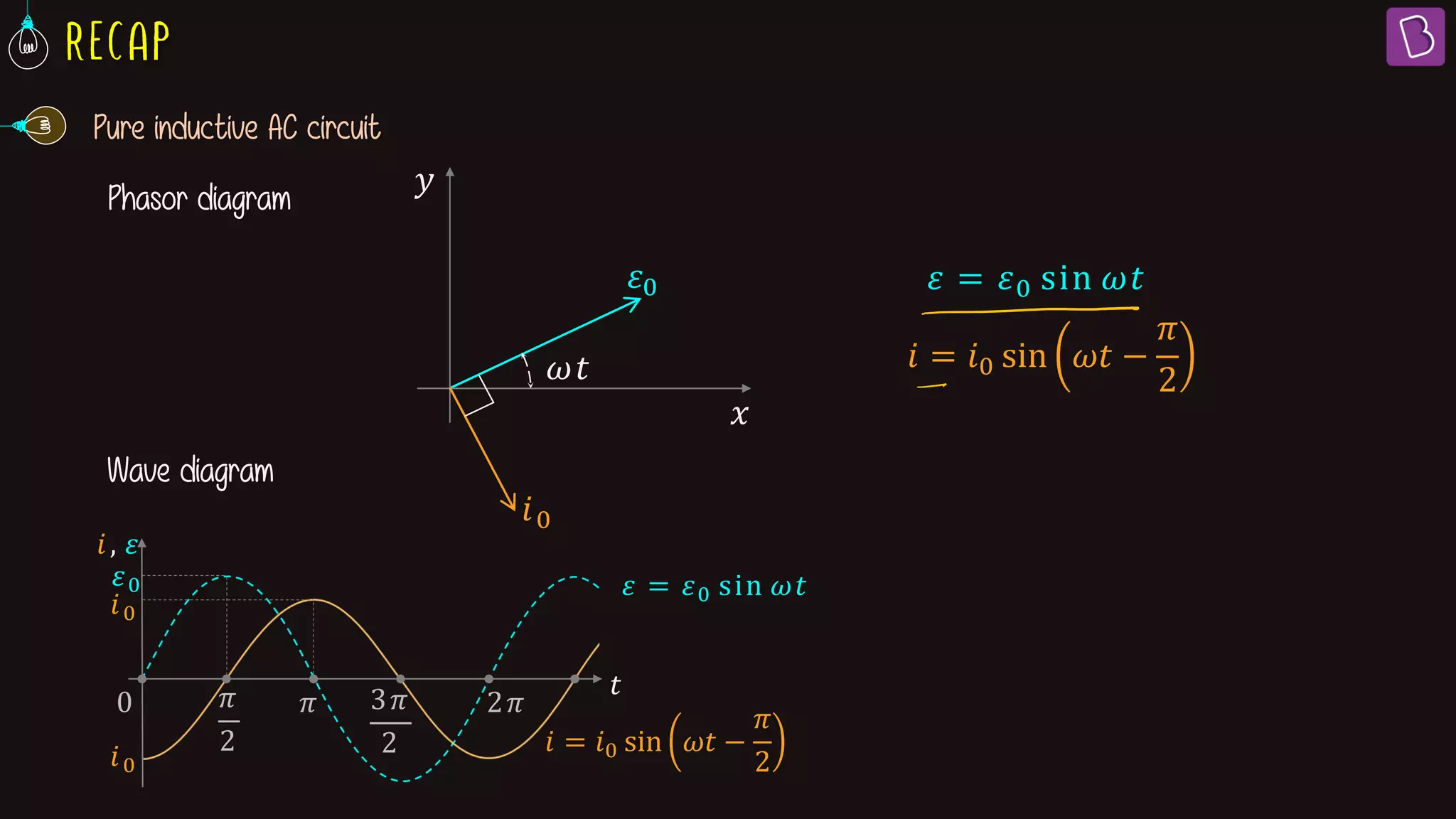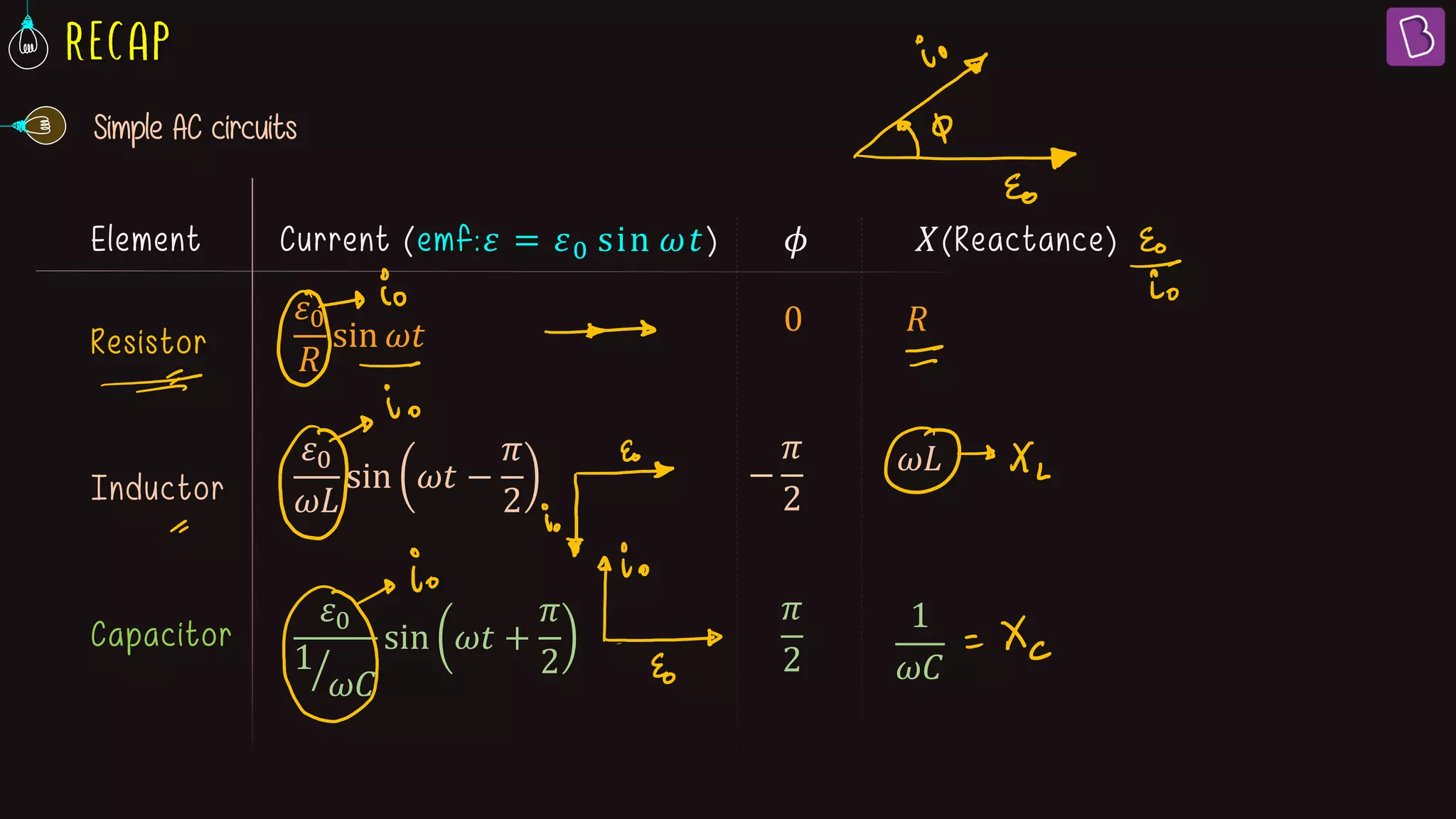This document discusses AC circuits containing resistors, inductors, and capacitors. It defines key terms like impedance, reactance, phase difference, and describes the behavior of pure resistive, inductive, and capacitive circuits. Graphs of voltage and current over time (wave diagrams) are provided to illustrate the phase relationships between them for each type of circuit. Formulas are given for calculating impedance, reactance, peak current and how current leads or lags voltage depending on the circuit elements. An example problem calculates values for an R-L circuit.