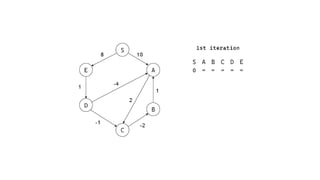
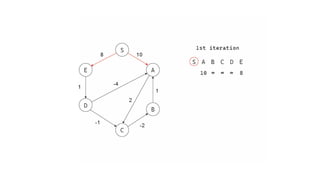
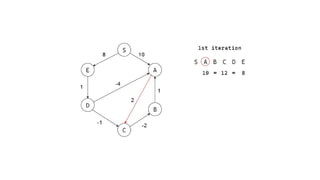
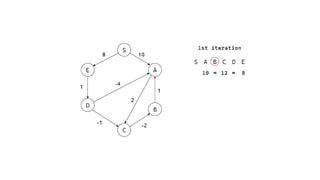
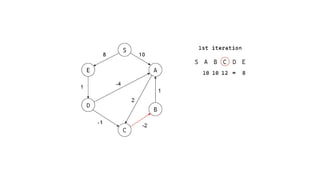
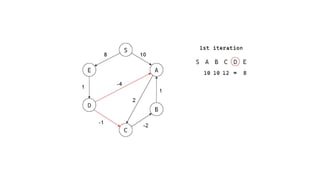
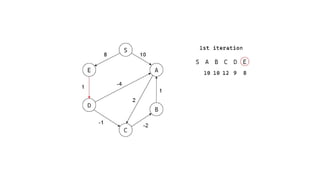
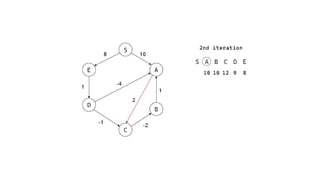
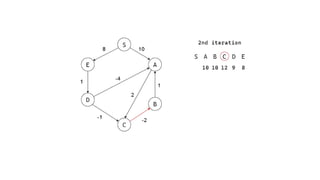
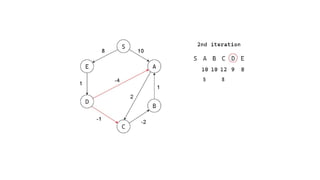
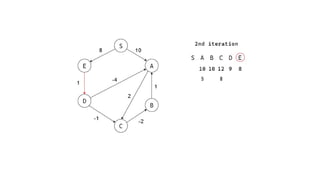
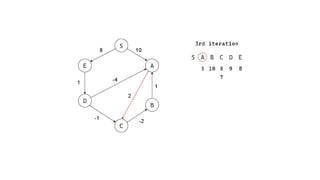
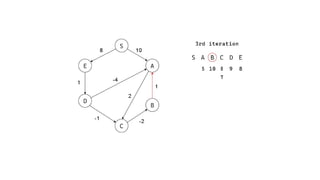
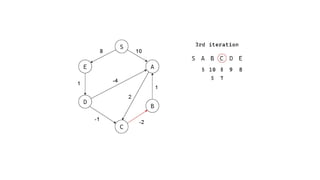
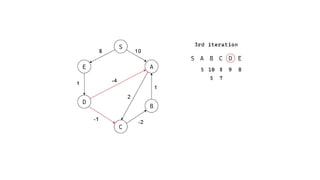
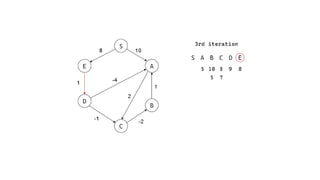
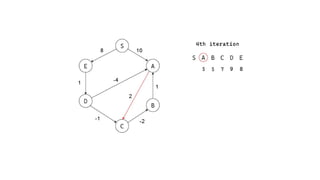
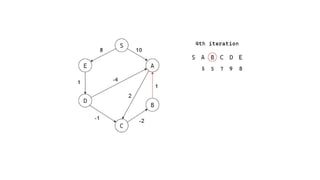
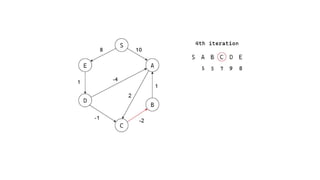
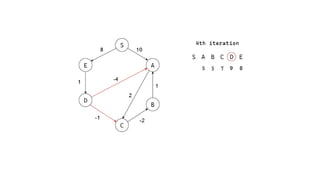
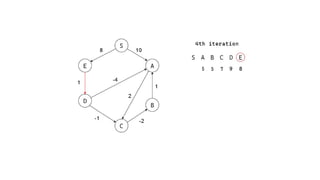
The Bellman-Ford algorithm is a key method in computer science for finding the shortest paths in weighted directed graphs, even when negative weights are present. It operates through initialization, relaxation of edges, and optimization of paths, with a time complexity of O(ve), which is higher than Dijkstra's algorithm that is more efficient for non-negative weights. The algorithm's ability to detect negative cycles makes it suitable for various real-world applications, including transportation and computer networks.

1. Bellman-Ford Algorithm
Abdulaziz Awwad Aljuaid
44108981
Supervised by
Dr. MD Masoud

2. What is it?
The Bellman-Ford algorithm is a fundamental technique in computer science and graph theory for
finding the shortest paths between a starting node and all other nodes in a weighted directed
graph, even in the presence of negative weights. This comprehensive guide will take you through
the key concepts, step-by-step explanation, time complexity analysis, and practical applications of
this powerful algorithm.

3. The Problem: Shortest Path with Negative
Weights
In many real-world applications, such as transportation networks, computer
networks, and social networks, we often need to find the shortest path
between two points.
This problem becomes more complex when the edges of the graph have
associated weights, representing the cost, distance, or time required to
traverse that edge.
The Bellman-Ford algorithm provides a solution to this problem, allowing us
to efficiently compute the shortest paths even when negative weights are
present.
Similar to Dijkstra’s algorithm, but it handles the negative weights and
detects cycles.

4. The Process
1 Initialization
The algorithm starts by initializing the distance to each vertex
from the source as "infinity", except for the source vertex
itself, which is set to 0.
2 Relaxation
It then repeatedly relaxes each edge, updating the distance to
the neighboring vertex if a shorter path is found. This process
is repeated n-1 times, where n is the number of vertices.
3 Optimizing Paths
The relaxation step ensures that the shortest paths are found
by iteratively improving the distance estimates to each vertex
until no further improvements are possible.
Relaxing condition:
If (d(u) + c(u, v) < d(v)):
d(v) = d(u) + c(u, v)

27. Complexity
Complexity: O(VE), where V is the number of vertices and E is the number of edges.
While Dijkstra’s Algorithm complexity is: O((V + E) * log(V)), using a priority queue for efficiency.
Bellman-Ford has a higher worst-case time complexity compared to Dijkstra's algorithm,
primarily due to its relaxation step that iterates through all edges for each vertex. Dijkstra's
algorithm, on the other hand, is more efficient for graphs with non-negative edge weights, as it
uses a priority queue to select the next vertex to relax based on the shortest known distance.

28. Reference
• Bellman Ford Shortest Path Algorithm – Baeldung
• Dijkstra’s vs Bellman-Ford Algorithm
• Bellman Ford Algorithm | Shortest path & Negative cycles | Graph Theo
ry