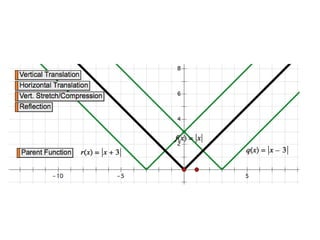
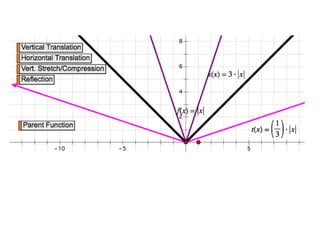
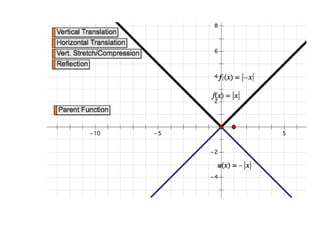
This document provides an overview of key concepts for graphing and understanding absolute value functions in Algebra II Chapter 2. It defines absolute value functions and their key features, including that the absolute value of f(x) gives the distance from the y-axis. Students will learn to graph absolute value functions by hand and using technology. The general form of an absolute value function is given as y = a|x - h| + k and examples are provided to show transformations from the standard form. Practice problems are assigned from the textbook.

1. Algebra II Chapter 2 Functions, Equations, and Graphs
© Tentinger

2.  Essential Understanding: Just as the absolute
value of x is its distance from zero, the absolute
value of f(x) or |f(x)|, gives the distance from the
line y = 0 for each value of f(x).
 Objectives:
 Students will be able to graph absolute value
functions

3.  F-IF.7. Graph functions expressed symbolically and show
key features of the graph, by hand in simple cases and
using technology for more complicated cases.★
 b. Graph square root, cube root, and piecewise-defined
functions, including step functions and absolute value
functions.
 F-BF.3. Identify the effect on the graph of replacing f(x) by
f(x) + k, k f(x), f(kx), and f(x + k) for specific values of k
(both positive and negative); find the value of k given the
graphs. Experiment with cases and illustrate an
explanation of the effects on the graph using technology.
Include recognizing even and odd functions from their
graphs and algebraic expressions for them.

4.  Absolute value function: f(x) = |x|
 Axis of symmetry: vertical line where the
graph is symmetric
 Vertex: either a single max or min point

5.  Use sketchpad
 General Equation: y = a|x - h| + k
 Describe the transformation(s) of the
equation and identify the axis of symmetry
and vertex.
 y = -2|x - 1| - 3
 y = 1/3|x + 4| + 1
 y = -|x + 2|

6.  Identify the vertex
 Identify a (what does a represent?)
 Write the equation in standard form

8.  2-7
 Pg. 111
 #9 – 30 (3s), 31, 35, 50, 54
 12 problems