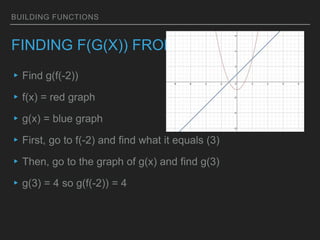
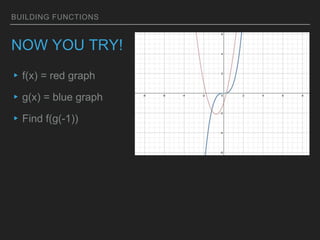
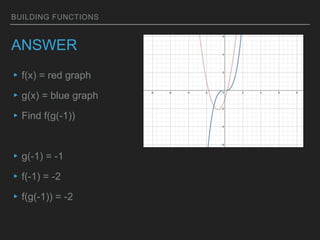
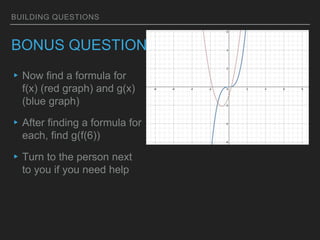
This document discusses building new functions from existing functions. It provides examples of replacing f(x) with f(x) + k, kf(x), f(kx), and f(x + k) and examining the effects on the graph. Students are asked to find inverse functions and verify functions are inverses of one another through composition. Examples are provided of evaluating composite functions f(g(x)) from graphs and algebraic expressions by first applying the inner function g(x) and then the outer function f(x).