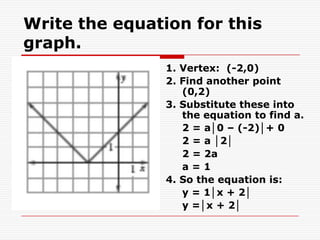
1. The document discusses absolute value functions of the form y = a|x - h| + k, where a ≠ 0. 2. It explains how to find the vertex (h, k) and line of symmetry x = h of an absolute value function graph. 3. It also describes how the graph opens up or down depending on whether a is positive or negative, and how the width compares to y = |x| depending on the value of |a|.

1. 2.8 Absolute Value
Functions
Today’s objective:
1. I will learn characteristics of absolute
value functions.
2. I will graph absolute value functions.
3. I will write the equation for an
absolute value function.

2. 2.8 Absolute Value Functions
 y = a│x – h │ + k,
a≠0
 The graph is shaped like a v.

3. Find the vertex
 Vertex: (h, k)
 h is always the opposite of the #
in the absolute value bars
 k is always the same as in the
equation

4. Line of symmetry
x=h
 Shown with a dashed vertical
line.

5. Graph opens up or down
 If a > 0:
 the graph opens up.
 the vertex (h, k) is the minimum.
 If a < 0:
 the graph opens down.
 the vertex (h, k) is the maximum.

6. Is the graph wider, narrower,
or the same width as y = │x│.
 Graph is narrower if │a │> 1.
 Graph is wider if 0 < │a │< 1.
 Graph is the same width if │a │ = 1.

7. Example: y = 3│ x + 2│ – 5
 The vertex is ( -2, -5), because the
opposite of 2 is -2, and k is – 5.
 The line of symmetry is x = -2
 The graph opens up because a > 0.
 The graph is narrower because│a│= 3
 The slope is 3, so start at the vertex
and go up 3 and to the right 1.
 Go back to the vertex. This time go up
3 and to the left 1.

8. Writing the equation for an
Absolute Value Function
1. Find the vertex (h,k)
2. Substitute this into the general form:
y = a│x – h │ + k
3. Find another point on the graph (x,y) and
substitute these values into the general
form.
4. Solve for a.
5. Write your equation. This time only
substitute the values of a, h, and k.

9. Write the equation for this
graph.
1. Vertex: (-2,0)
2. Find another point
(0,2)
3. Substitute these into
the equation to find a.
2 = a│0 – (-2)│+ 0
2 = a │2│
2 = 2a
a=1
4. So the equation is:
y = 1│x + 2│
y =│x + 2│