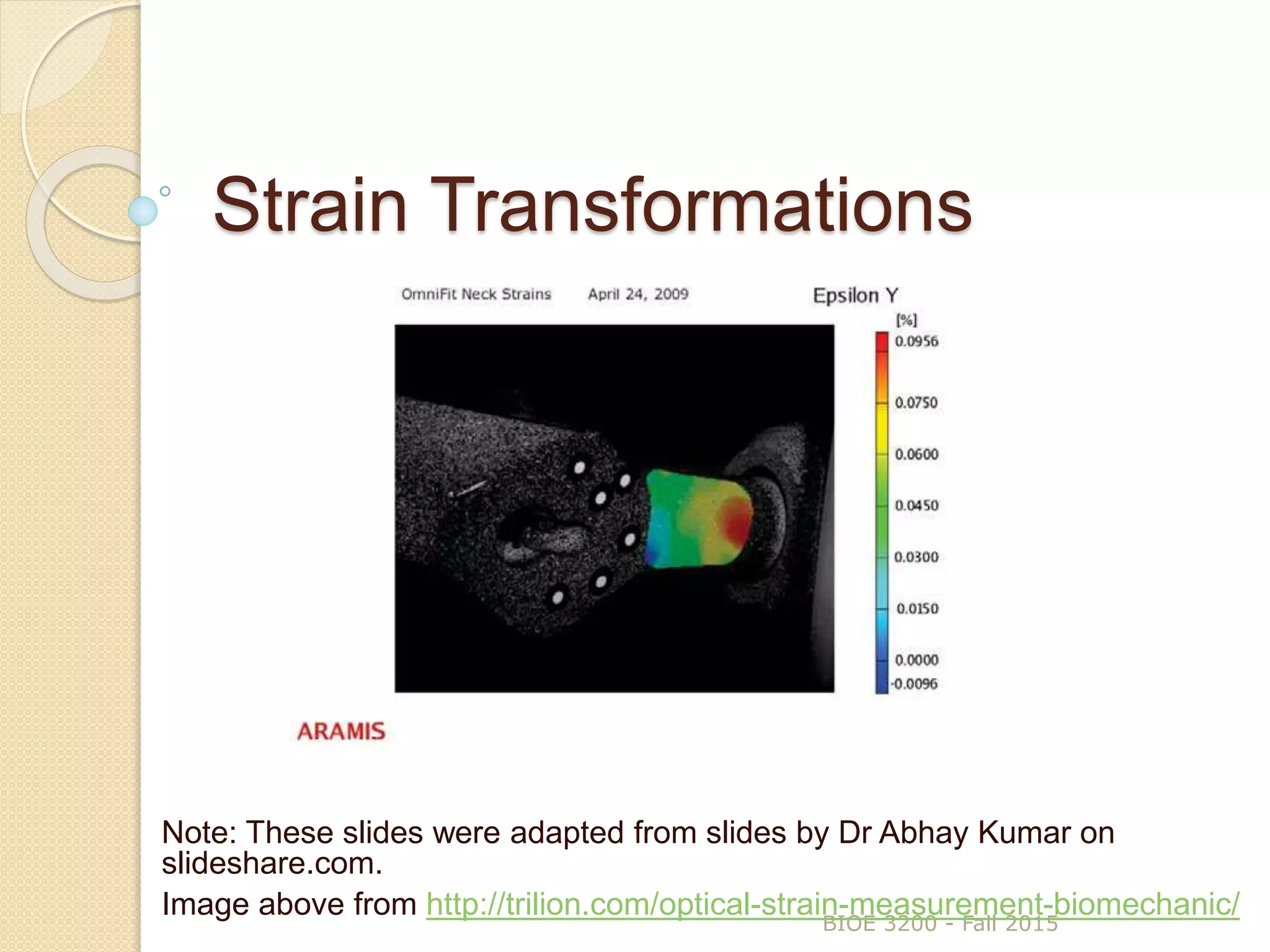
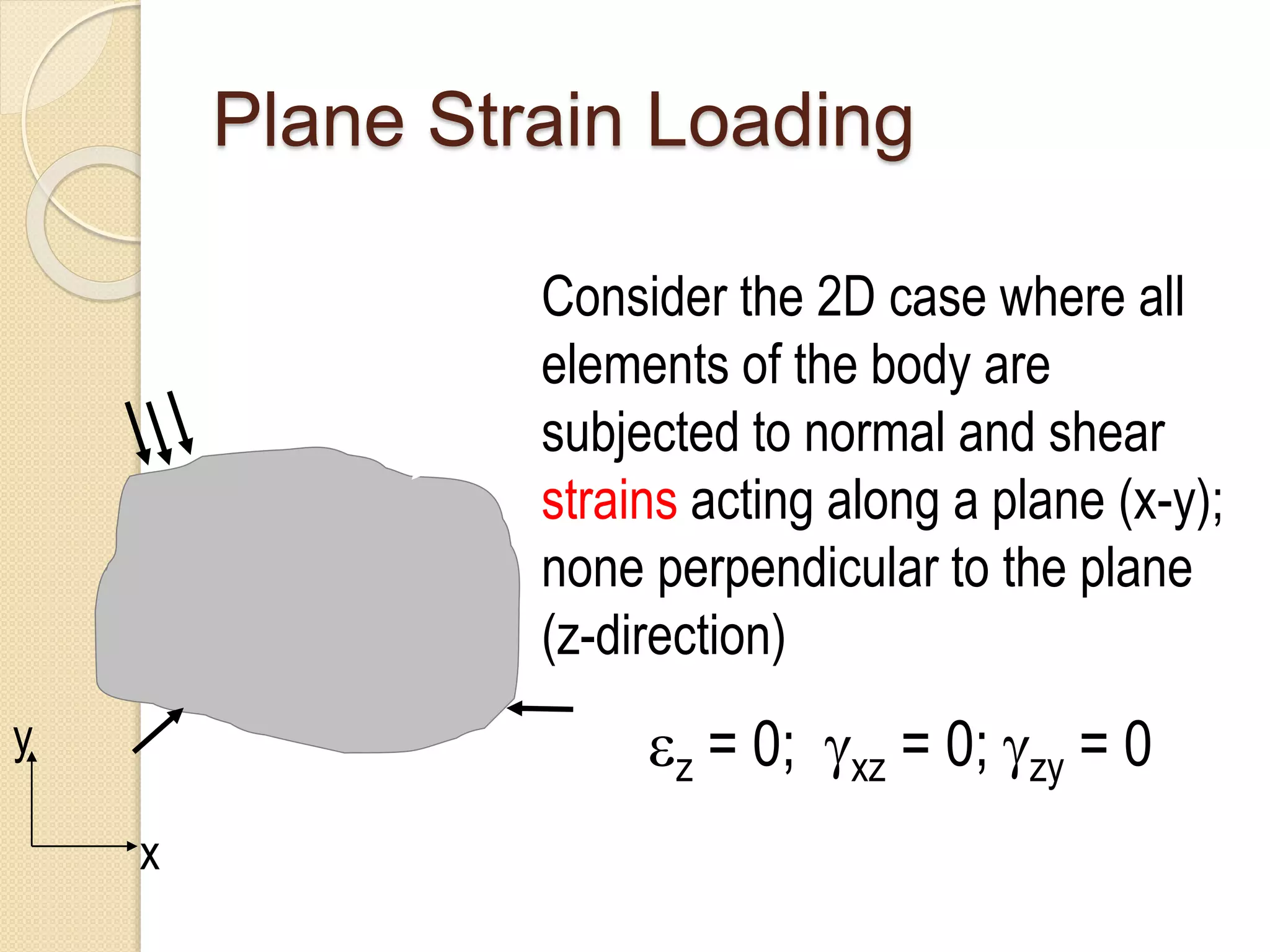
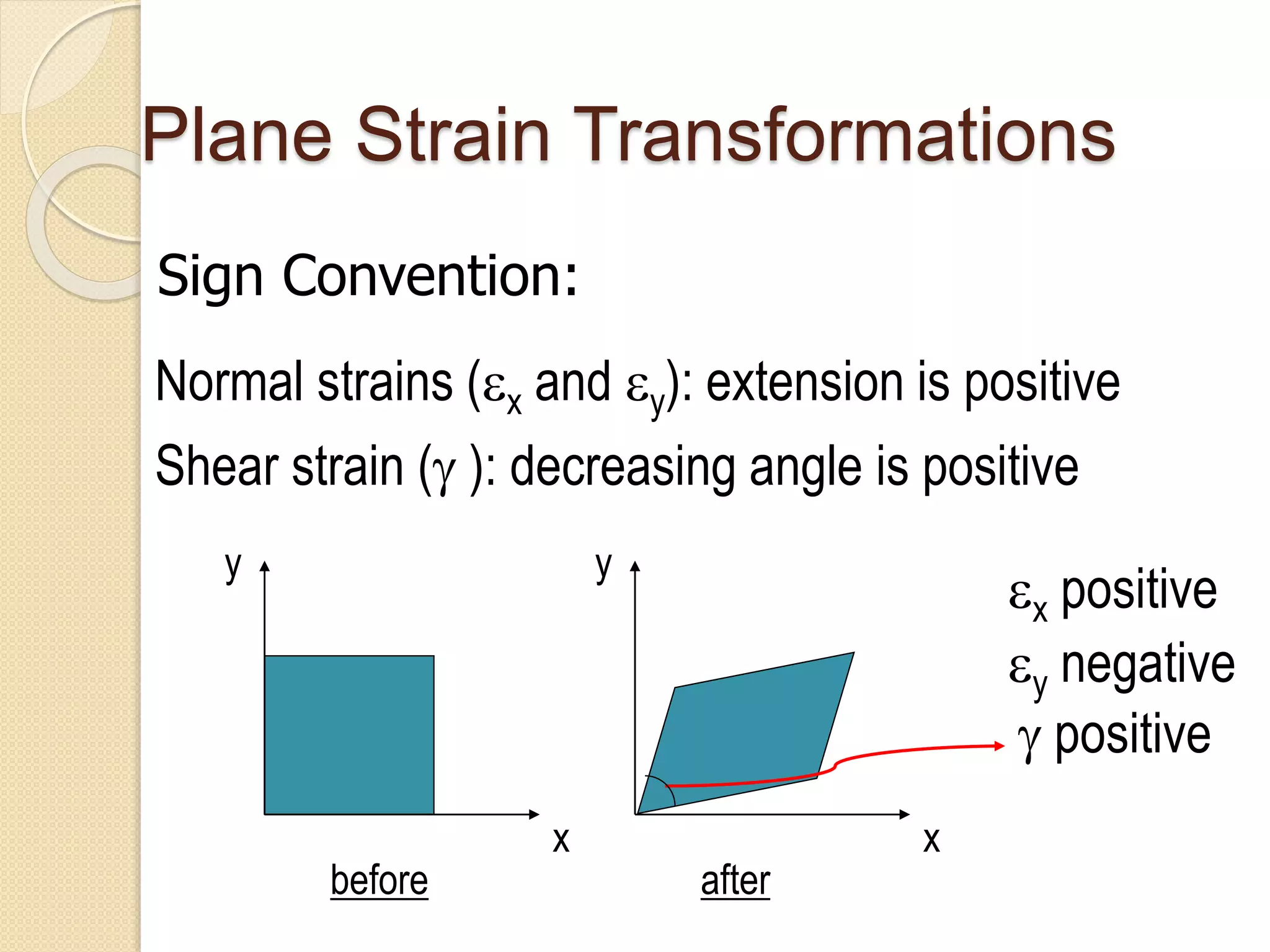
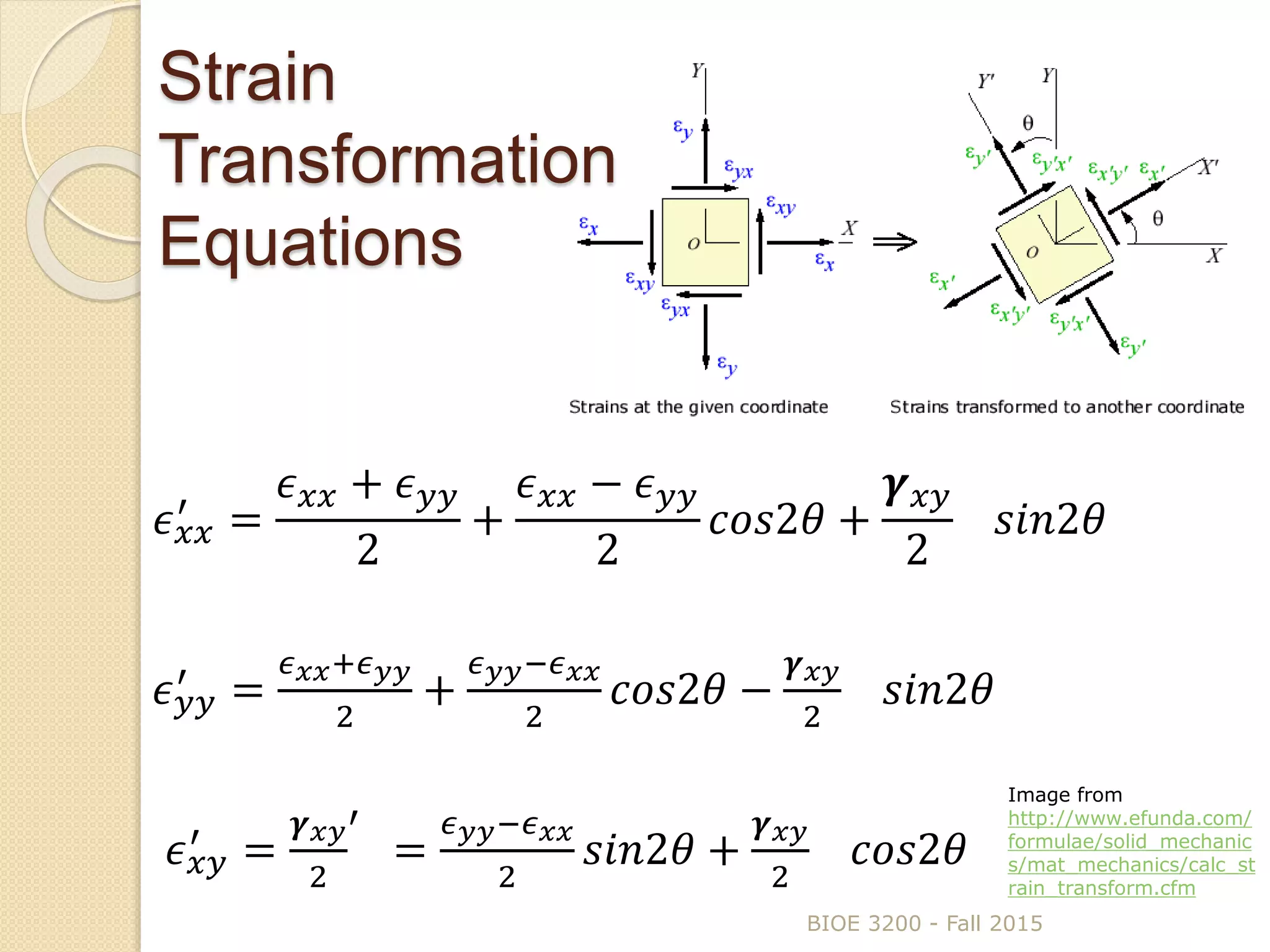
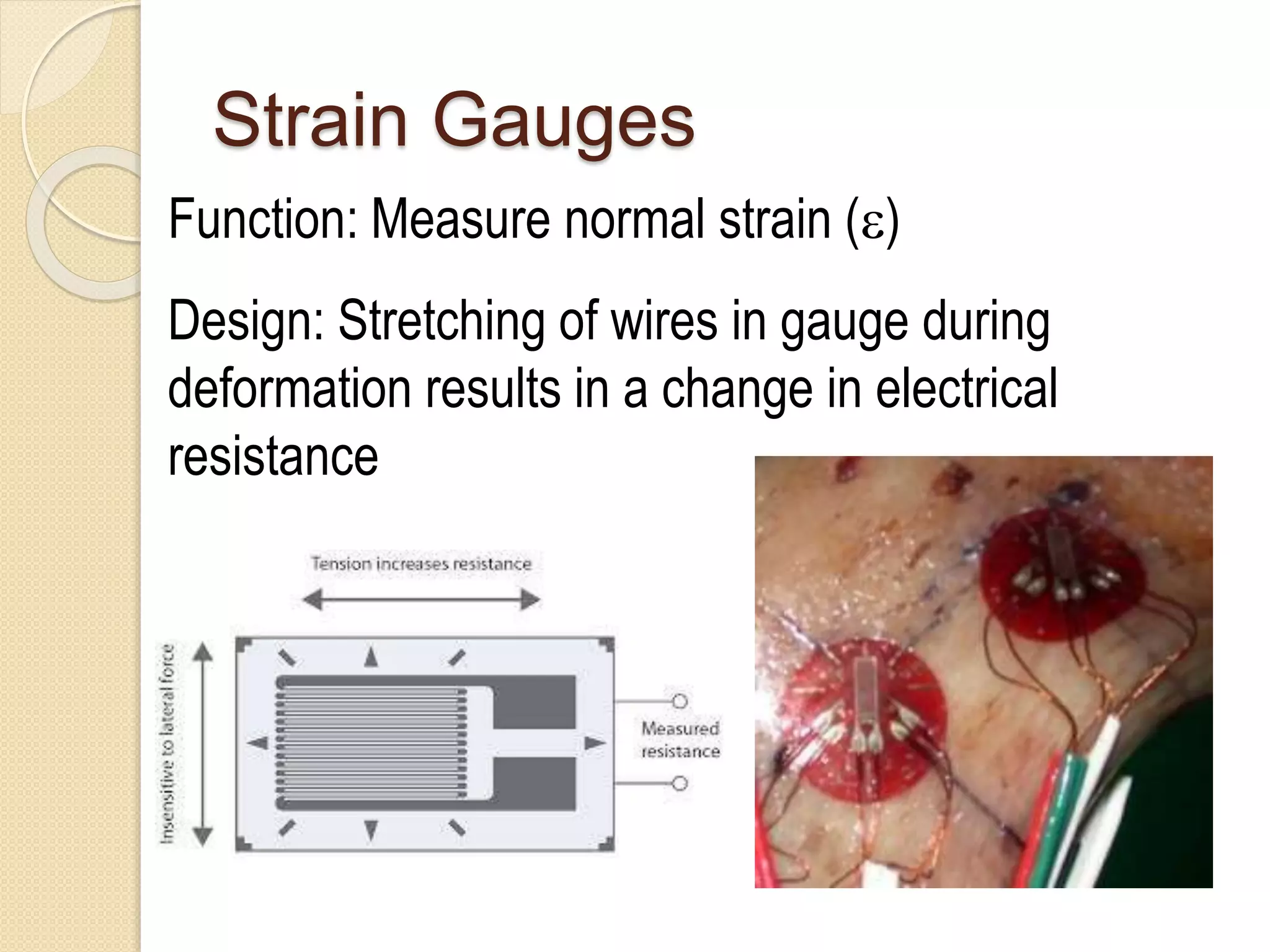
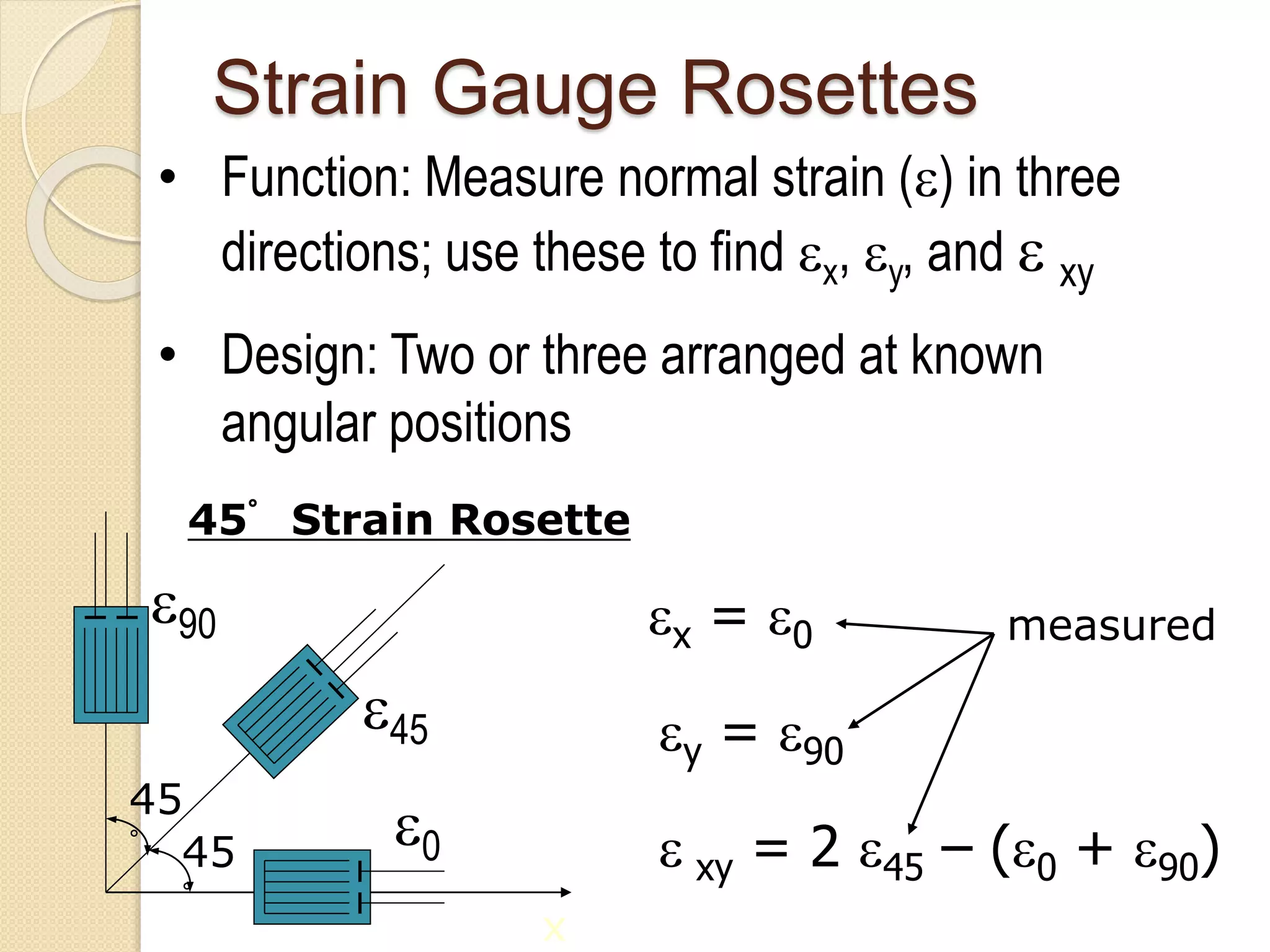
The document discusses strain transformations within a rigid body, focusing on methods to calculate strains in multiple planes and the function and application of strain gauges. It includes equations for plane strain transformations and the design and use of strain gauge rosettes to measure strains in various directions. Practical applications highlighted include measuring strains in devices and validating computer models.

1. Strain Transformations
BIOE 3200 - Fall 2015
Note: These slides were adapted from slides by Dr Abhay Kumar on
slideshare.com.
Image above from http://trilion.com/optical-strain-measurement-biomechanic/

2. Learning objectives
 Calculate strains in multiple planes
(strain transformations) within a rigid
body
 Describe the function, design, and
application of a strain gauge.
BIOE 3200 - Fall 2015

3. Plane Strain Loading
x
y
Consider the 2D case where all
elements of the body are
subjected to normal and shear
strains acting along a plane (x-y);
none perpendicular to the plane
(z-direction)
z = 0; xz = 0; zy = 0

4. x
y
x’
y’
A
State of Stress at A
 x
y
xy
xy
’x=?
’xy=?
Plane Strain Transformations
Similar to derivation of equations for stress
transformation, replacing:
 by , and
 by /2

5. Plane Strain Transformations
Sign Convention:
Shear strain ( ): decreasing angle is positive
Normal strains (x and y): extension is positive
x
y
before
x
y
after
x positive
y negative
 positive

6. Strain
Transformation
Equations
𝜖 𝑥𝑥
′
=
𝜖 𝑥𝑥 + 𝜖 𝑦𝑦
2
+
𝜖 𝑥𝑥 − 𝜖 𝑦𝑦
2
𝑐𝑜𝑠2𝜃 +
𝜸 𝑥𝑦
2
𝑠𝑖𝑛2𝜃
𝜖 𝑦𝑦
′
=
𝜖 𝑥𝑥+𝜖 𝑦𝑦
2
+
𝜖 𝑦𝑦−𝜖 𝑥𝑥
2
𝑐𝑜𝑠2𝜃 −
𝜸 𝑥𝑦
2
𝑠𝑖𝑛2𝜃
𝜖 𝑥𝑦
′
=
𝜸 𝑥𝑦
2
′
=
𝜖 𝑦𝑦−𝜖 𝑥𝑥
2
𝑠𝑖𝑛2𝜃 +
𝜸 𝑥𝑦
2
𝑐𝑜𝑠2𝜃
BIOE 3200 - Fall 2015
Image from
http://www.efunda.com/
formulae/solid_mechanic
s/mat_mechanics/calc_st
rain_transform.cfm

7. Strain Gauges
Function: Measure normal strain ()
Design: Stretching of wires in gauge during
deformation results in a change in electrical
resistance

8. Strain Gauge Rosettes
• Function: Measure normal strain () in three
directions; use these to find x, y, and  xy
• Design: Two or three arranged at known
angular positions
45° Strain Rosette
x
45
°
45
° 0
90
45
x = 0
y = 90
 xy = 2 45 – (0 + 90)
measured

9. Strain gauge applications
 Measuring strains in devices or
structures
◦ Strain gauges for snow board testing:
https://www.youtube.com/watch?v=h1CvL
ZQABjE
◦ Strain gauges in human motion research:
http://file.scirp.org/Html/7-
4000046_33327.htm
 Validating computer models and
predicted strains
BIOE 3200 - Fall 2015