Advanced Engineering Mathematics

Advanced Engineering
Mathematics
Dr.A.Emamzadeh
aemamzadeh2004@yahoo.com
١

Reference texts
[1] Faires & Burden Numerical Methods 3rd ed. ,Brooks/Cole 2003
[2] Froberg
Introductions to Numerical Analysis, Addison-
Wesley
٢

Content
Title Page
Introduction 5
IVP method 6
Extrapolation 36
BVP method 55
Linear system solver 87
Variational methods 93
Eigen value problems 100
PDE methods 105
Spline interpolation 130
Nonlinear systems 139
٣

Ordinary Differential Equations
1) Introduction
2) Initial Value Problems (IVP)
3) Boundary Value Problems (BVP)
٤

1) Introduction
1- Sources of errors
1.1- Initial data error
1.2- Round off error
1.3- Truncation error
2- Type of problems
2.1- well – behaved
2.2- ill – conditioned
3- Stability
4- Big Oh
٥

2) Methods of solving IVP
1- Introduction
2- Taylor series method
3- Single step methods
4- Multi step methods
5- Extrapolation methods
٦

3) Methods of solving BVP
1- Shooting methods
2- Finite difference methods
3- Variational methods
4- Eigen Value Problems (EVP)
٧

Types of problems in IVP
 Single first order equation
 System of n first order equations
 Single n th order equation
٨

Single first order equation
, with initial condition (IC),
)
,
( y
x
f
y =
′
0
0 )
( y
x
y =
To find y at x1 to a specified accuracy.
٩

System of n first order equations
),
,...,
,
(
)
,...,
,
(
1
1
1
1
n
n
n
n
y
y
x
f
y
y
y
x
f
y
=
′
=
′

With initial conditions
0
0
10
0
1
)
(
)
(
n
n y
x
y
y
x
y
=
=

To find y1,…yn at x1 to a specified accuracy.
١٠

Where [ ]t
n
1 y
,
,
y
Y 
=
and [ ]t
n
1 f
,
,
f
F 
=
In matrix form
0
0 Y
)
Y(x
Y)
F(x,
Y
=
=
′
١١

Single n th order equation
),
,
,
,
,
,
( )
1
(
)
( −
′
′
′
= n
n
y
y
y
y
x
f
y 
with initial conditions
0
0
)
1
(
10
0 )
(
,
,
)
( n
n
y
x
y
y
x
y =
= −

This equation with the given initial conditions can be
transformed into a system of n first order equations
as follows,
١٢

Let n
n
y
y
y
y
y
y =
=
′
= − )
1
(
2
1  then
( )
n
n y
y
y
x
f
y ,
,
,
, 2
1 
=
′
and
0
0
10
0
1 )
(
,
)
( n
n y
x
y
y
x
y =
= 
The whole system can be written in the matrix form
0
0 )
(
)
,
(
Y
x
Y
Y
x
F
Y
=
=
′
Where [ ] [ ]t
n
t
n f
y
y
y
F
y
y
Y ,
,
,
,
,
, 3
2
1 
 =
= and
١٣

Finally we are dealing with the form
0
0 )
(
)
,
(
y
x
y
y
x
f
y
=
=
′ as a single first order equation or
as a system of n first order equations
١٤

Taylor series method
0
0 )
(
)
,
(
y
x
y
y
x
f
y
=
=
′ To find y at x1 correct to md
Let x1 – x0 = h then the Taylor expansion of y about
x = x0 is
( ) ( ) 
+
′
′
′
+
′
′
+
′
+
=
+
= y
h
y
h
y
h
y
h
x
y
x
y
!
3
!
2
3
0
2
0
0
0
1
١٥

0
0
0
0
0
0
0
0
)
,
(














∂
∂
+
∂
∂
∂
∂
+








∂
∂
+
∂
∂
∂
∂
=
′
′
′






∂
∂
+
∂
∂
=
′
′
=
′
y
f
f
x
f
y
f
y
f
f
x
f
x
y
y
f
f
x
f
y
y
x
f
y
y given
is
here
١٦

( )
( ) 2
0
1
0
3 2
−
=
′
=
−
+
=
′
′
y
y
y
x
y
Given
:
Example
on
so
and
Find y(h) correct to 2d where h=0.1, 0.5,1 and 2.
١٧

( )
( ) 14
)
0
(
3
2
12
)
0
(
2
5
)
0
(
2
1
2
)
0
(
)
5
(
)
5
(
)
4
(
2
)
4
(
=
⇒
′
′
′
+
′
′
′
−
=
−
=
⇒
′
′
+
′
−
=
=
′
′
′
⇒
′
−
=
′
′
′
=
′
′
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
have
we
( ) 
+
+
−
+
+
−
= 5
4
3
2
60
7
2
1
6
5
2
1 h
h
h
h
h
h
y
١٨

Taking number of terms n=6
When h=0.1 y(0.1)=.8107845000
h=0.5 y(0.5)=.3265625000
h=1 y(1)=.4500000000
h=2 y(2)=3.400000000
Taking number of terms n=7
y(0.1)= .8107846111
y(0.5)= .3282986111
y(1)= .5611111111
y(2)= 10.51111111
١٩

Taking n=10
y(0.1)= .8107846019
y(0.5)= .3276448999
y(1.0)= .4951609347
y(2.0)= 9.887477949
Compare the accuracy
٢٠

Single step methods
Def.:
Local truncation error
Global truncation error
Order of a method
First order method (Euler's method)
Statement of the problem
( )
( ) 0
0
,
y
x
y
y
x
f
y
=
=
′
given
٢١

To find y at x=b correct to md
Let b-x0=h then
( ) ( ) ( )
2
0
0
0
0
0 , h
y
x
f
h
y
y
h
y
b
y o
+
+
=
′
+
=
Here O(h2) is the local truncation error
In the standard form
( ) 
,
1
,
0
,
1
1
1
=
=
+
=
+
n
y
x
f
h
k
k
y
y
n
n
n
n where
٢٢

Second order methods
( )
( )
( ) error
truncation
global
the
is
and
where
1.
2
1
2
1
2
2
1
2
,
2
,
h
O
k
y
h
x
f
h
k
y
x
f
h
k
h
O
k
y
y
n
n
n
n
n
n






+
+
=
=
+
+
=
+
٢٣

( )
( )
( )
( ) g.t.e.
before
as
where
2.
2
1
2
1
2
2
1
1
,
,
2
1
2
1
h
O
k
y
h
x
f
h
k
y
x
f
h
k
h
O
k
k
y
y
n
n
n
n
n
n
+
+
=
=
+
+
+
=
+
٢٤

A third order method
( ) ( )
( )
( )
1
2
3
1
2
1
3
3
2
1
1
2
,
2
,
2
,
,
2
,
1
4
6
1
k
k
y
h
x
f
h
k
k
y
h
x
f
h
k
y
x
f
h
k
n
h
O
k
k
k
y
y
n
n
n
n
n
n
n
n
−
+
+
=






+
+
=
=
=
+
+
+
+
=
+
where

٢٥

A 4th order method (runge – kutta)
( ) ( )
( )
( )
3
4
2
3
1
2
1
4
4
3
2
1
1
,
2
,
2
2
,
2
,
2
2
6
1
k
y
h
x
f
h
k
k
y
h
x
f
h
k
k
y
h
x
f
h
k
y
x
f
h
k
h
O
k
k
k
k
y
y
n
n
n
n
n
n
n
n
n
n
+
+
=






+
+
=






+
+
=
=
+
+
+
+
+
=
+
where
٢٦

Example:
( )
( ) ( ) 2
0
,
1
0
2
sin
=
′
=
′
+
+
=
′
′
y
y
y
y
x
y
Find y(0.1) and y’(0.1) using h=0.1 and a 2nd order
method.
( )
( )
( ) 2
0
1
0
2
sin
=
=
+
+
=
′
=
′
p
y
p
y
x
p
p
y then
Let
٢٧

Take k for the slope of y and l for the slope of p
then
( )
( )
( )
( ) ( ) ( ) ( )
[ ]
1
0
1
0
0
2
1
0
2
0
0
0
1
0
1
2
1
0
1
2
1
0
1
2
sin
2
sin
2
1
2
1
l
p
k
y
h
x
h
l
l
p
h
k
p
y
x
h
l
p
h
k
l
l
p
p
k
k
y
y
+
+
+
+
+
=
+
=
+
+
=
=
+
+
=
+
+
=
where
Now calculate [Note the argument of sine must the in
radiance].
٢٨

Modified Euler's method
( )
( ) ( )
[ ] ( )
( ) g.t.e.
the
is
where
2
2
1
1
1
1
,
,
2
,
h
O
h
O
y
x
f
y
x
f
h
y
y
y
x
f
h
y
y
p
n
n
n
n
n
c
n
n
n
n
p
n
+
+
+
=
+
=
+
+
+
+
( ) ( )
( ) error.
truncation
local
the
is
where
2
2
1 ,
2
h
O
h
O
y
x
hf
y
y n
n
n
n +
+
= −
+1
Mid - Point rule
٢٩

How to control the truncation error
1) By lowering the step size and repeat the
whole calculations: Runge-Kutta method
2) By considering the 1st neglected term in
the Taylor expansion:
Merson’s method
A 2nd and third order method
Fehlberge’s method
٣٠

A single-step method with error estimator
Merson’s method
( ) ( )
( )
( )
5
4
3
1
4
3
1
5
3
1
4
2
1
3
1
2
1
5
5
4
1
1
8
9
2
30
1
2
2
3
2
,
8
3
8
,
2
6
6
,
3
3
,
3
,
4
6
1
k
k
k
k
E
k
k
k
y
h
x
hf
k
k
k
y
h
x
hf
k
k
k
y
h
x
hf
k
h
y
h
x
hf
k
y
x
hf
k
h
O
k
k
k
y
y
n
n
n
n
n
n
n
n
n
n
n
n
−
+
−
=






+
−
+
+
=






+
+
+
=






+
+
+
=






+
+
=
=
+
+
+
+
=
+
where
٣١

Fehlberg method
( )






−
+
−
+
−
+
=






−
+
−
+
=






+
−
+
+
=






+
+
+
=






+
+
=
=
−
+
+
+
=
+
−
+
+
+
=
+
+
5
4
3
2
1
6
4
3
2
1
5
3
2
1
4
2
1
3
1
2
1
5
4
3
1
1
6
5
4
3
1
1
~
40
11
4104
1859
2565
3544
2
27
8
,
2
4104
845
513
3680
8
216
439
,
2197
7296
2197
7200
2197
1932
,
13
12
32
9
32
3
,
8
3
4
1
,
4
,
5
1
4104
2197
2565
1408
216
25
55
2
50
9
56430
28561
12825
6656
135
16
k
k
k
k
k
y
h
x
hf
k
k
k
k
k
y
h
x
hf
k
k
k
k
y
h
x
hf
k
k
k
y
h
x
hf
k
k
y
h
x
hf
k
y
x
hf
k
k
k
k
k
y
y
k
k
k
k
k
y
y
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
where
٣٢

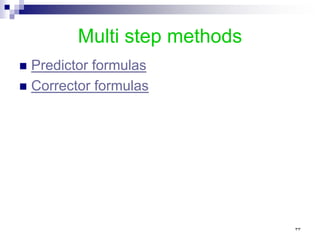
Multi step methods
 Predictor formulas
 Corrector formulas
٣٣

Predictor formulas






−
+
−
+
−
+
=






+
−
+
−
+
=






−
+
−
+
=






+
−
+
=






−
+
=
+
=
−
−
−
−
−
+
−
−
−
−
+
−
−
−
+
−
−
+
−
+
+
5
4
3
2
1
1
4
3
2
1
1
3
2
1
1
2
1
1
1
1
1
1440
475
1440
2877
1440
7298
1440
9982
1140
7923
1140
4277
720
251
720
1274
720
2616
720
2774
720
1901
24
9
24
37
24
59
24
55
12
5
12
16
12
23
2
1
2
3
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
f
f
f
f
f
f
h
y
y
f
f
f
f
f
h
y
y
f
f
f
f
h
y
y
f
f
f
h
y
y
f
f
h
y
y
f
h
y
y
٣٤

Corrector formulas






+
−
+
−
+
+
=






−
+
−
+
+
=






+
−
+
+
=






−
+
+
=






+
+
=
−
−
−
−
+
+
−
−
−
+
+
−
−
+
+
−
+
+
+
+
4
3
2
1
1
1
3
2
1
1
1
2
1
1
1
1
1
1
1
1
1440
27
1440
173
1440
482
1440
798
1440
1427
1440
475
720
19
720
106
720
264
720
646
720
251
24
1
24
5
24
19
24
9
12
1
12
8
12
5
2
1
2
1
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
f
f
f
f
f
f
h
y
y
f
f
f
f
f
h
y
y
f
f
f
f
h
y
y
f
f
f
h
y
y
f
f
h
y
y
٣٥

Extrapolation methods
1.Introduction:
Consider calculating π as the area of a unit circle
(Fig.1), by calculation of the area of n sided
polygon inscribed in the circle.
n
θ
1
Fig. 1
n
A0
Let be the area of n sided polygon.






=
=
n
n
n
A n
n π
θ
2
sin
2
sin
2
0
٣٦

Using Taylor expansion of Sin x


+
+
+
+
=












+






−






+






−
=
6
6
4
4
2
2
7
5
3
0
!
7
2
!
5
2
!
3
2
2
2
n
a
n
a
n
a
n
n
n
n
n
An
π
π
π
π
π
Where a2, a4, a6, … are constants, do not depend on n.
Now if we double n then

+
+
+
+
= 6
6
4
4
2
2
2
0
64
16
4 n
a
n
a
n
a
A n
π
٣٧

To form a linear combination of
in such away that in the linear combination
the first term be π and the second term
vanishes, that is, for some α and β
n
n
A
A 2
0
0 and

+
+
+
+
=
=
+ 8
8
6
6
4
4
1
2
0
0
n
b
n
b
n
b
A
A
A n
say
n
n
π
β
α
Where b4, b6, b8, … are constants, do not depend on n.
0
4
1 =
+
=
+
β
α
β
α and
Then
The implies that
3
4
3
1 =
−
= β
α and
٣٨

To go further we can repeat the same procedure
by doubling the sides again and hence.

+
+
+
+
= 8
8
6
6
4
4
2
1
256
64
16 n
b
n
b
n
b
A n
π
Again to form a linear combination of
in such away that in the linear combination the first term be
p and the second term vanishes, that is for some α and β.
n
n
A
A 2
1
1 and
,
8
8
6
6
2
2
1
1 
+
+
+
=
=
+
n
c
n
c
A
A
A n
say
n
n
π
β
α
٣٩

Where c6, c8, … are constants, do not depend
on n.
,
8
8
6
6
2
2
1
1 
+
+
+
=
=
+
n
c
n
c
A
A
A n
say
n
n
π
β
α

1,2,
n
for
and
general
In
and
that
implies
this
and
Then
=
−
=
−
−
=
=
−
=
=
+
=
+
1
4
4
1
4
1
15
16
15
1
,
0
16
1
n
n
n
β
α
β
α
β
α
β
α
٤٠

The result of above operations can be
presented in an extrapolation table as
follows.
n
n
n
n
n
n
n
n
n
n
A
A
A
A
A
A
A
A
A
A
3
2
2
4
1
8
0
2
2
1
4
0
1
2
0
0 3
1
−
3
4
15
1
−
15
16
Note that truncation error of the columns respectively are
on.
so
and

,
1
,
1
,
1
6
4
2 

















n
O
n
O
n
O
63
1
−
63
64
٤١

Numerically
1. Starting with a triangle (the least accuracy),
we have
Are these coefficients (α and β) general?
=
3
0
A
=
6
0
A
=
12
0
A
=
24
0
A
=
48
0
A
1.299038
2.598077
3.000001
3.105829
3.132629
3.03109
3.133975
3.141105
3.141563
3.140834
3.141581
3.141593
3.141593
3.141593 3.141593
٤٢

=
4
0
A
=
8
0
A
=
16
0
A
=
32
0
A
=
64
0
A
2
2.828427
3.061468
3.121446
3.136549
3.10457
3.139148
3.141439
3.141584
3.141453
3.141591
3.141593
3.141593
3.141593 3.141593
٤٣

=
5
0
A
=
10
0
A
=
20
0
A
=
40
0
A
=
80
0
A
2. 377642
2.938927
3.09017
3.12869
3.138364
3.126022
3.140584
3.3014153
3.141489
3.141555
3.141593
3.141593
3.141593
3.141594 3.141594
=
160
0
A 3.140786 3.141593 3.141593 3.141593 3.141593 3.141593
٤٤

=
10
0
A
=
20
0
A
=
40
0
A
=
80
0
A
=
160
0
A
2. 938926
3.09017
3.12869
3.138364
3.140786
3.140584
3.14153
3.141589
3.141593
3.141593
3.141593
3.141593
3.141593
3.141593 3.141593
=
320
0
A 3.141391 3.141593 3.141593 3.141593 3.141593 3.141593
٤٥

1. yes, whenever the accuracy parameter
is changed by factor of 2. and the terms
of the Taylor expansion are alternatively
zero.
2. No otherwise
٤٦

Extrapolation in differentiation
Starting with central difference formula for
the first and second derivative
( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( ) )
2
(
2
)
1
(
2
2
2
2
h
O
h
h
x
f
x
f
h
x
f
x
f
h
O
h
h
x
f
h
x
f
x
f
+
−
+
−
+
=
′
′
+
−
−
+
=
′
Denote the RHS of (1) as and the RHS of (2) as
h
F0
h
S0
٤٧

Similar extrapolation table looks like
h
h
h
h
h
h
F
F
F
F
F
F
2
2
1
4
0
1
2
0
0 3
1
−
3
4
15
1
−
15
16
The truncation error of the columns in order are
( ) ( ) ( ) .
on
so
and
and
6
4
2
, h
O
h
O
h
O
Similarly for the second derivative
٤٨

Extrapolation in integration
Consider the trapezoidal rule
( ) ( )






+
+
=
+
=
∑
∫
−
=
1
1
0
0
2
0
2
2
n
i
i
n
h
h
b
a
f
f
f
h
T
h
O
T
dx
x
f
where
h
h
h
h
h
h
T
T
T
T
T
T
2
2
1
4
0
1
2
0
0 3
1
−
3
4
15
1
−
15
16
٤٩

Extrapolation in IVP
Suppose y'=f(x,y) , y(x0)=y0 to find y(b)
correct to md, with extrapolation method.
Start with Mid-Point rule
( ) ( )
2
0
0
1
1 ,
2 h
O
y
x
hf
y
y +
+
= −
Either y-1is known previously or it should be
calculated by, say, Euler's method and corrected by
modified Euler's method to have the same accuracy
as O(h2)
٥٠

therefore with h<0
( )
( ) ( )
[ ]
E
c
E
y
x
f
y
x
f
h
y
y
y
x
hf
y
y
1
1
0
0
0
1
0
0
0
1
,
,
2
,
−
−
−
−
+
−
=
−
=
and
If we denote then in extrapolation notation
h
Y
y 0
1 by
h
h
h
h
h
h
Y
Y
Y
Y
Y
Y
2
2
1
4
0
1
2
0
0 3
1
−
3
4
15
1
−
15
16
٥١

And so on.
Compare this method with single step
methods and multi step methods.
٥٢

Example
Consider y'=y , y(0)=1 . To find y(1)
correct to 3d .
start with h=1 , y0=1 , x0=0
[ ]
2
1
0
2
1
1
1
1
0
1
1
8
21
8
13
1
8
13
1
8
5
8
5
2
1
1
4
1
1
2
1
2
1
1
2
1
5
.
2
2
2
1
2
1
0
1
2
1
1
,
0
Y
y
y
y
y
h
Y
y
y
c
E
c
E
=
=
+
=
=
+
=
=






+
−
=
=
−
=
=
=
+
=
=
+
−
=
=
−
−
−
−
with
٥٣

To continue calculate and and
extrapolate.
6666
.
2
6
16
2
7
6
5
8
21
3
4
2
5
3
1
3
4
3
1 2
1
0
1
0
1
1
=
=
+
−
=






+






−
=
+
−
= Y
Y
Y
4
1
0
Y 8
1
0
Y
٥٤

Shooting methods
Statement of a boundary value problem
( )
( ) ( )



=
=
′
=
′
′
β
α b
y
a
y
y
y
x
f
y
,
,
,
Given
Find y for a<x<b correct to md.
Shooting method changes the BVP into an IVP by assuming
a value for y'(a) , say S, then using a root finder to find the
root of y(b,S)-β=0 up to a desired accuracy.
1. Secant method
2. Newton’s method
٥٥

Let us start with secant method as the root finder
Step 1. Guess S0=y'(a)
Step 2. Solve the IVP
( ) ( ) ( ) ,
,
,
,
, 0
S
a
y
a
y
y
y
x
f
y =
′
=
′
=
′
′ α
to find y(b, S0) .
Is y(b, S0)=β ? if yes then stop, otherwise continue
( ) ( )
( ) ( ) β
β
>
<
′
=
<
>
′
=
0
0
1
0
0
1
,
,
S
b
y
if
S
a
y
S
S
b
y
if
S
a
y
S otherwise
Guess
( ) ( ) ( ) ,
,
,
,
, 1
S
a
y
a
y
y
y
x
f
y =
′
=
′
=
′
′ α
to find y(b, S1).
Step 3.
٥٦

Is y(b, S1)=β ? If yes then stop, otherwise continue.
Step 5. Find the next Sn+1 ,using secant method.
( )
[ ]( )
( ) ( )

,
2
,
1
,
,
,
1
1
1 =
−
−
−
−
=
−
−
+ n
S
b
y
S
b
y
S
S
S
b
y
S
S
n
n
n
n
n
n
n
β
( ) ( ) ( )
( )
1
1
,
,
,
,
,
,
+
+
=
′
=
′
=
′
′
n
n
S
b
y
S
a
y
a
y
y
y
x
f
y
find
to
α
Step 7. Test for convergence
( ) stop
then
yes
if
Is Tol
S
b
y n <
−
+ β
1
,
Step 8. Go to step 5.
٥٧

Example 1:
Given ( )
( ) 3
1
,
3
2
1
2
2
=
=






−
′
−
=
′
′
y
y
y
x
y [note that this is a linear differential equation]
To find y for 1
2
1
<
< x correct to 3d.
( )
( )
[ ]
( ) 0001
.
3
,
1
2
7500
.
3
6250
.
3
2
1
3
6250
.
3
2
1
6250
.
3
,
1
2
1
7500
.
3
,
1
1
2
2
0
1
0
0
=
−
=
−






−
−
−
=
=
=
=
=
S
y
S
S
y
S
S
y
S
٥٨

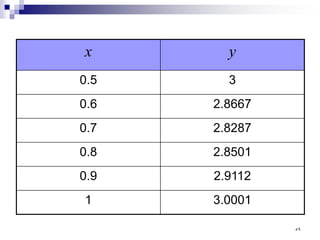
x y
0.5 3
0.6 2.8667
0.7 2.8287
0.8 2.8501
0.9 2.9112
1 3.0001
٥٩

Example 2:
Given
( ) ( ) 8
2
,
4
1
2
1
=
=







 ′
+
′
=
′
′
y
y
y
y
x
y
y [this is a nonlinear differential equation]
To find y for 1<x<2 correct to 3d.
( ) ( )
( )
[ ]( )
( ) ( )

,
2
,
1
,
2
,
2
8
,
2
0
8
,
2
1
1
1 =
−
−
−
−
=
=
−
=
−
−
+ n
S
y
S
y
S
S
S
y
S
S
S
y
S
F
n
n
n
n
n
n
n
٦٠

( )
( )
( )
( )
( )
( )
( ) 000000
.
8
,
2
333333
.
1
9902356
.
7
,
2
3331706
.
1
9688716
.
7
,
2
328125
.
1
2580645
.
8
,
2
375
.
1
111111
.
7
,
2
16667
.
1
4
.
6
,
2
1
16
,
2
2
6
6
5
5
4
4
3
3
2
2
1
1
0
0
=
=
=
=
=
=
=
=
=
=
=
=
=
=
S
y
S
S
y
S
S
y
S
S
y
S
S
y
S
S
y
S
S
y
S
٦١

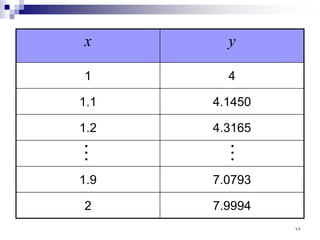
x y
1 4
1.1 4.1450
1.2 4.3165
1.9 7.0793
2 7.9994
 
٦٢

In case of Newton's method as the root finder the steps will be
as follows
Step 1. Guess S0=y'(a)
Step 2. Solve the system
( )
( )
( )
( )
( )













=
∂
′
∂
=
∂
∂
=
′
=
∂
′
∂
⋅
′
∂
∂
+
∂
∂
⋅
∂
∂
=
∂
′
′
∂
′
=
′
′
1
0
,
,
0
S
a
y
S
a
y
S
a
y
a
y
S
y
y
f
S
y
y
f
S
y
y
y
x
f
y
α (1)
٦٣

By any IVP method find y(b, S0), y' (b, S0) and
( ) ( )
0
0 ,
,
, S
b
S
y
S
b
S
y
∂
′
∂
∂
∂
Step 3. Find a new Sn using Newton’s method
( )
( )

,
1
,
0
,
,
1 =
∂
∂
−
−
=
+ n
S
b
s
y
S
b
y
S
S
n
n
n
n
β
Step 4. Solve the system(1) with new Sn=y'(a)
Step 5. Test for convergence, i.e.
( ) stop
then
yes
if
Tol
S
b
y n <
− β
,
٦٤

Step 6. Go to step 3.
Example: Find y for 1<x<2, given
( ) ( )
then
and
denote
us
let
system(1)
solve
to
now
guess
U
S
y
Y
S
y
S
y
y
y
y
x
y
y
=
∂
′
∂
=
∂
∂
=
=
=







 ′
+
′
=
′
′
2
8
2
,
4
1
2
1
0
٦٥

if
( )
( )
( )
( ) 1
1
0
1
1
4
1
4
1
2
2
1
0
2
2
=
=
=
=
⋅








+
+
⋅
−
=
′
=
′








+
=
′
=
′
U
Y
S
p
y
U
y
p
x
Y
y
p
U
U
Y
y
p
x
p
p
p
y then
٦٦

Solve by 4th order Runge-Kutta with h=0.01 (say) then
( ) ( )
66666667
.
1
24
,
2
16
,
2
1
0
0
=
=
∂
∂
=
S
S
S
y
S
y
implies
this
and
Next five iterations yields
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( ) ( ) 000000
.
6
,
2
000000
.
8
,
2
33333333
.
1
00018279
.
6
,
2
00012208
.
8
,
2
333353689
.
1
04715063
.
6
,
2
03137248
.
8
,
2
33854166
.
1
82666667
.
6
,
2
5333333
.
8
,
2
416666667
.
1
6666667
.
10
,
2
6666667
.
10
,
2
66666667
.
1
5
5
5
4
4
4
3
3
3
2
2
2
1
1
1
=
∂
∂
=
=
=
∂
∂
=
=
=
∂
∂
=
=
=
∂
∂
=
=
=
∂
∂
=
=
S
S
y
S
y
S
S
S
y
S
y
S
S
S
y
S
y
S
S
S
y
S
y
S
S
S
y
S
y
S
٦٧

Finite difference methods
Statement of the problem:
Given the BVP
( )
( ) ( ) β
α =
=
′
=
′
′
b
y
a
y
y
y
x
f
y
,
,
,
Find y for a<x<b correct to md.
There are two cases:
1. Linear equation, in general
( ) ( ) ( )
( ) ( ) β
α =
=
+
+
′
=
′
′
b
y
a
y
x
r
y
x
q
y
x
p
y
,
٦٨

2. Non linear equation
( )
( ) ( ) β
α =
=
′
=
′
′
b
y
a
y
y
y
x
f
y
,
,
,
The above two cases are called BVPs with separated
boundary conditions.
BVP with general linear boundary values are of the
form
( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) 5
4
3
2
1
5
4
3
2
1
,
,
B
b
y
B
b
y
B
a
y
B
a
y
B
A
b
y
A
b
y
A
a
y
A
a
y
A
y
y
x
f
y
=
′
+
+
′
+
=
′
+
+
′
+
′
=
′
′
٦٩

BVP with general boundary conditions are of
the form
( )
( ) ( ) ( ) ( )
( )
( ) ( ) ( ) ( )
( ) 0
,
,
,
,
0
,
,
,
,
,
,
2
1
=
′
′
=
′
′
′
=
′
′
b
y
b
y
a
y
a
y
b
g
b
y
b
y
a
y
a
y
a
g
y
y
x
f
y
The idea of finite difference methods is to discretise
the equation by dividing the interval [a,b] into n
equal divisions, i.e.
h
n
a
b say
==
−
٧٠

b
x
n
i
ih
x
x
a
x n
i =
−
=
+
=
= ,
1
,
,
1
, 0
0 
then
The BVP becomes
( )
β
α =
=
=
′
=
′
′
n
i
i
i
i
y
y
a
x
y
y
x
f
y
,
,
,
,
0
0
Now we replace the derivatives by an approximate
value of finite difference such as:
٧١

4
2
1
1
2
3
2
1
1
2
2
1
1
1
1
4
6
4
2
2
2
2
2
h
y
y
y
y
y
y
h
y
y
y
y
y
h
y
y
y
y
h
y
y
y
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
−
−
+
+
−
−
+
+
−
+
−
+
+
−
+
−
=
′
′
′
′
−
+
−
=
′
′
′
+
−
=
′
′
−
=
′
Central-difference expressions with error of order h2
٧٢

Central-difference expressions with error of order h4
4
3
2
1
1
2
3
3
3
2
1
1
2
3
2
2
1
1
2
2
1
1
2
6
12
39
56
39
12
8
8
13
13
8
12
16
30
16
12
8
8
h
y
y
y
y
y
y
y
y
h
y
y
y
y
y
y
y
h
y
y
y
y
y
y
h
y
y
y
y
y
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
−
−
−
+
+
+
−
−
−
+
+
+
−
−
+
+
−
−
+
+
−
+
−
+
−
+
−
=
′
′
′
′
+
−
+
−
+
−
=
′
′
′
−
+
−
+
−
=
′
′
+
−
+
−
=
′
٧٣

Forward-difference expressions with error of order h
4
1
2
3
4
3
1
2
3
2
1
2
1
4
6
4
3
3
2
h
y
y
y
y
y
y
h
y
y
y
y
y
h
y
y
y
y
h
y
y
y
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
+
−
+
−
=
′
′
′
′
+
+
−
=
′
′
′
+
−
=
′
′
−
=
′
+
+
+
+
+
+
+
+
+
+
٧٤

4
1
2
3
4
5
3
1
2
3
4
2
1
2
3
1
2
3
14
26
24
11
2
2
5
18
24
14
3
2
5
4
2
3
4
h
y
y
y
y
y
y
y
h
y
y
y
y
y
y
h
y
y
y
y
y
h
y
y
y
y
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
+
−
+
−
+
−
=
′
′
′
′
−
+
−
+
−
=
′
′
′
+
−
+
−
=
′
′
−
+
−
=
′
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Forward-difference expressions with error of order h2
٧٥

Backward-difference expressions with error of order h
4
4
3
2
1
3
3
2
1
2
2
1
1
4
6
4
3
3
2
h
y
y
y
y
y
y
h
y
y
y
y
y
h
y
y
y
y
h
y
y
y
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
−
−
−
−
−
−
−
−
−
−
+
−
+
−
=
′
′
′
′
−
+
−
=
′
′
′
+
−
=
′
′
−
=
′
٧٦

4
5
4
3
2
1
3
4
3
2
1
2
3
2
1
2
1
2
11
24
26
14
3
2
3
14
24
18
5
4
5
2
2
4
3
h
y
y
y
y
y
y
y
h
y
y
y
y
y
y
h
y
y
y
y
y
h
y
y
y
y
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
+
−
+
−
=
′
′
′
′
+
−
+
−
=
′
′
′
−
+
−
=
′
′
+
−
=
′
Backward-difference expressions with error of order h2
٧٧

In linear case we have, using the central difference
forms with truncation error of O(h2),
( ) ( ) ( )
1
,
,
1
,
2
2
0
1
1
2
1
1
−
=
=
=
+
+
−
=
+
− −
+
−
+
n
i
y
y
x
r
y
x
q
h
y
y
x
p
h
y
y
y
n
i
i
i
i
i
i
i
i
i

β
α
After some simplifications
1
,
,
1
,
0
1
1
−
=
=
=
=
+
+ +
−
n
i
y
y
D
y
C
y
B
y
A
n
i
i
i
i
i
i
i

β
α
Where
i
i
i
i
i
i
i
i
r
h
D
hp
C
q
h
B
hp
A
2
2
2
2
2
4
2
=
+
=
−
−
=
−
=
٧٨

In matrix form
















−
−
=
































−
−
−
−
−
β
α
1
1
2
1
1
1
2
1
1
1
2
2
2
1
1
n
n
n
n
n
C
D
D
A
D
y
y
y
B
A
C
B
A
C
B
O
O









This linear system can be solved by
1.Direct methods (gauss elimination, …)
2.Iterative methods (Jacobi's method, Gauss
Seidel method, Successive Over Relaxation
method, SOR). ٧٩

Example:
( )
( )
3d.
to
correct
for
Find 1
2
1
3
1
,
3
2
1
2
2
<
<
=
=






−
′
−
=
′
′
x
y
y
y
y
x
y
Take n=5 ⇒ h=0.1 then
٨٠













−
−
=
























−
−
−
−
96
.
2
04
.
0
04
.
0
46
.
1
8
.
1
8
.
0
0
0
9
.
0
6
.
1
7
.
0
0
0
8
.
0
4
.
1
6
.
0
0
0
7
.
0
2
.
1
4
3
2
1
y
y
y
y
Using Gauss elimination method
91111111
.
2
85000000
.
2
8285714
.
2
866666667
.
2
4
3
2
1
=
=
=
=
y
y
y
y
٨١

In non linear case, using central difference
formulas with truncation error O(h2)
( )
( )
1
,
,
1
,
,
2
/
,
,
2
0
1
1
2
1
1
−
=
=
=
−
=
+
− −
+
−
+
n
i
y
y
h
y
y
y
x
f
h
y
y
y
n
i
i
i
i
i
i
i

β
α
Using simple iteration method, with suitable initial
guess
( )


,
1
,
0
1
,
,
1
,
2
,
,
2
2
1
0
)
1
(
1
)
(
1
)
(
2
)
(
1
)
1
(
1
1
=
−
=
=
=







 −
−
+
=
+
−
+
+
+
−
+
k
n
i
y
y
h
y
y
y
x
f
h
y
y
y
n
k
i
k
i
k
i
i
k
i
k
i
k
i
β
α
٨٢

Example:
( ) ( ) 8
2
,
4
1
2
1
=
=







 ′
+
′
=
′
′
y
y
y
y
x
y
y
Find y for 1<x<2 correct to 5d.
Upon discritisation we have,
( )

 ,
1
,
0
,
1
,
,
1
8
,
4
1
2
2
2
1
0
)
(
)
1
(
1
)
(
1
)
1
(
1
)
(
1
2
)
(
1
)
1
(
1
)
1
(
=
−
=
=
=





 −
+





 −
−
+
=
+
−
+
+
−
+
+
+
−
+
k
n
i
y
y
y
h
y
y
x
h
y
y
h
y
y
y
n
k
i
k
i
k
i
i
k
i
k
i
k
i
k
i
k
i
٨٣

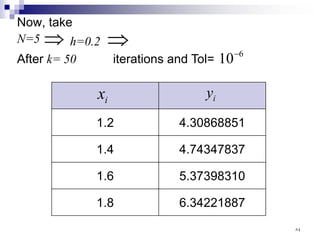
Now, take
N=5 ⇒ h=0.2 ⇒
After k= 50 iterations and Tol=
6
10−
1.2 4.30868851
1.4 4.74347837
1.6 5.37398310
1.8 6.34221887
i
x i
y
٨٤

Take N=10 ⇒ h=0.1
After k= iterations
1.1
1.2 4.31464627
1.3
1.4 4.75747894
1.5
1.6 5.39795103
1.7
1.8 6.37355180
1.9
i
x i
y
٨٥

To improve the accuracy
1. Either increase n smaller h
Larger system of equations
2. Use extrapolation,
In the above example
⇒ ⇒
Improved ( )
3
1
4
.
1 −
=
y less accurate ( )
3
4
4
.
1 +
y more accurate y(1.4)
( ) ( )
( )
4
762145797
.
4
75747894
.
4
3
4
74347837
.
4
3
1
h
O
+
=
+
−
=
Continue to improve accuracy.
٨٦

Iterative methods for system of linear equations.
To solve
1) Ax=b
Where












=












=












=
n
n
nn
n
n
b
b
b
x
x
a
a
a
a
A









 1
1
1
1
11
,
,x
2)
n
n
nn
n
n
n
b
x
a
x
a
b
x
a
x
a
=
+
+
=
+
+



1
1
1
1
1
11
3)
n
i
b
x
a
n
i
b
x
a
x
a
n
j
i
j
ij
i
n
in
i
,
,
1
,
,
1
1
1
1



=
=
=
=
+
+
∑
=
4)
٨٧

Pivoting , Scaling
Jacobi’s method: guess n
i
xi ,
,
1
)
0
(

=



=
=










−
= ∑
≠
=
+


,
1
,
0
,
,
1
1
1
)
(
)
1
(
k
n
i
x
a
b
a
x
n
i
j
j
k
j
ij
i
ii
k
i
Test for convergence at each iteration
Tol
x
x k
j
k
j <
−
+ )
(
)
1
(
For all j=1,…,n
٨٨

Guess – Seidel method



,
1
,
0
,
,
,
1
1
,
,
1
1
)
(
1
1
)
1
(
)
1
(
)
0
(
=
=






−
−
=
=
∑
∑ +
=
−
=
+
+
k
n
i
x
a
x
a
b
a
x
n
i
x
n
i
j
k
j
ij
i
j
k
j
ij
i
ii
k
i
i
Guess
Test for convergence
٨٩

Successive Over Relaxation (SOR)
method



,
1
,
0
,
,
,
1
,
,
1
)
(
1
1
)
1
(
)
(
)
1
(
)
0
(
=
=






−
−
+
=
=
∑
∑ =
−
=
+
+
k
n
i
x
a
x
a
b
a
x
x
n
i
x
n
i
j
k
j
ij
i
j
k
j
ij
i
ii
k
i
k
i
i
ω
Guess
Test for convergence
required?
is
or b
opt ω
ω .
٩٠

1. No general formula for
2. depends on the form of A.
3. 0< <2
When 1< <2 we have over relaxation and when
0< <1 we have under relaxation
4. to be calculated numerically.
b
ω
b
ω
b
ω
b
ω
b
ω
b
ω
٩١

Example: solve












−
−
=
























−
−
−
−
96
.
2
04
.
0
46
.
1
8
.
1
8
.
0
0
0
9
.
0
6
.
1
7
.
0
0
0
8
.
0
4
.
1
6
.
0
0
0
7
.
0
2
.
1
4
3
2
1

x
x
x
x
w 1 1.1 1.2 1.3 1.4 1.5 1.6
k 34 27 21 15 18 24 30
b
w
Minimum
When k=14
28
.
1
=
ω ٩٢

Variational methods
 Introduction
Distance between two points
[ ] ( ) ( )
∫ ∫ 





+
=
+
=
2
1
2
1
2
2
2
1
x
x
x
x
dx
dx
dy
dy
dx
y
I
To minimize I[y] set its derivative to zero.
There are certain restrictions on each y which must
pass through ,etc.
( ) ( )
2
2
1
1 ,
, y
x
y
x &
2
y
1
y
1
x 2
x
4
y
3
y 2
y
1
y
٩٣

E-L eqn. ( ) ( )
y
y
x
F
y
y
y
x
F
y
dx
d
′
∂
∂
=






′
′
∂
∂
,
,
,
,
If F is independent of 0
=
∂
∂
⇒
′
y
F
y
If F is independent of C
y
F
y
F
dx
d
y =
′
∂
∂
⇒
=








′
∂
∂
⇒ 0
If F is independent of
0
=






′
∂
∂
′
−
=
′
∂
∂
′
−
⇒
y
F
y
F
dx
d
C
y
F
y
F
x
or
٩٤

Now to solve the BVP
( )
[ ] ( ) ( )
( ) ( ) 0
1
0 =
=
=
+
′
′
−
y
y
x
f
y
x
q
y
x
p
The Rayleigh - Ritz method minimizes the E-L
equation
[ ] ( ) ( )
[ ] ( ) ( )
[ ] ( ) ( )
{ }
∫ −
+
′
=
1
0
2
2
2 dx
x
u
x
f
x
u
x
q
x
u
x
p
u
I
Choose u to be a linear combination of some basis
function such as few first terms of Taylor expansion
or in general ∑
= i
i
c
u φ
٩٥

Where are chosen in such away to satisfy the
boundary conditions
Now for minimization find
and equate to zero
These are called the normal equations which can be
solved by a method of linear systems.
i
φ
( ) ( )
[ ]
0
1
0 =
= i
i φ
φ
n
i
c
I
i
,
,
1 
=
∂
∂
n
i
c
I
i
,
,
1
0 
=
=
∂
∂
٩٦

Example:
Let us choose the basis to be the linear functions
( )









≤
<
≤
<
−
<
<
−
≤
≤
=
+
+
+
−
−
−
−
1
0
0
0
1
1
1
1
1
1
1
x
x
x
x
x
h
x
x
x
x
x
h
x
x
x
x
x
i
i
i
i
i
i
i
i
i
i
i
i
φ
( )
x
i
φ
x
0
1
1
−
i
x i
x 1
+
i
x 1
٩٧

The normal equations yield a tridiagonal linear
system which can be solved by previously
introduced methods.
Example:
( ) ( ) 0
1
0
4
2
2 2
2
=
=
−
=
+
′
−
′
′
−
y
y
x
y
y
x
y
x
Given
Use h=0.1 and linear approximation.
Now given
( )
( ) ( ) 0
=
=
=
+
′
′
b
y
a
y
x
f
Qy
y
٩٨

Then E-L equation
[ ] [ ]
{ }
∫ +
−
′
=
b
a
dx
fu
Qu
u
u
I 2
2
2
to be minimized.
B.C.
&
If
2
2
1
0 x
c
x
c
c
u +
+
=
2
1
0
2
1
0
,
0
,
0
,
0 c
c
c
c
I
c
I
c
I
gives
then =
∂
∂
=
∂
∂
=
∂
∂
B.C.
&
If
3
3
2
2
1
0 x
c
x
c
x
c
c
u +
+
+
=
on.
so
&
gives
then 3
,
2
,
1
,
0
3
,
2
,
1
,
0
0 =
=
=
∂
∂
i
c
i
c
I
i
i
٩٩

Eigen Value Problems
(Homogeneous BVP)
Consider the problem:
( ) ( ) 0
1
0
2
=
=
−
=
′
′
y
y
y
y λ
To find the nontrivial solution of the above system
( )
( )
{ } 

,
2
,
1
,
2
,
1
0
sin
0
sin
0
1
sin
0
0
sin
cos
=
=
∴
=
=
⇒
=
⇒
=
⇒
=
=
⇒
=
+
=
k
k
k
k
B
y
x
B
y
y
x
B
x
A
y
k π
λ
π
λ
λ
λ
λ
λ
λ
B.C.
&
B.C.
&
١٠٠

The Eigen Values are
and are the Eigen functions.
Let us use finite difference method
2
2
2
π
λ k
k =
x
B
y k
k
k λ
sin
=
1
,
,
1
0
2
0
2
2
1
1
−
=
=
=
−
=
=
− −
+
n
i
y
y
y
h
y
y
y
n
i
i
i
i

λ
In matrix form, let t
h =
+
− 2
2
2 λ
















=
































− 0
0
1
1
1
1
1
1
1
1










n
y
y
t
t
t
O
O
١٠١

This homogeneous linear system has nontrivial
solution when
( ) 0
1
1
1
1
1
det =
=
t
t
t
A
O
O





Choosing n=2 then 2
1
=
h
and an approximation
to the analytical value
8
0 2
=
⇒
= λ
t
8696
.
9
2
2
1 =
= π
λ
١٠٢

Choosing n=4 then 4
1
=
h







=
+
=
=
=
−
=
⇒
=
6274
.
54
2
2
32
3726
.
9
2
2
0
1
0
1
1
0
1
2
3
2
2
2
1
λ
λ
λ
t
t
t
and
The analytical value of
8264
.
88
4784
.
39
8696
.
9
2
3
2
2
2
1
=
=
=
λ
λ
λ
١٠٣

Again for improvement there are two
methods
1) To increase n and have smaller h leading
to a higher degree polynomial equation
and hence more round off error.
2) To use extrapolation technique.
In this case
Improved ( ) ( )
( ) ( )
8301
.
9
3726
.
9
3
4
8
3
1
3
4
3
1 2
1
2
1
2
1
=
+
−
=
+
−
= λ
λ
λ accurate
more
accurate
less
١٠٤

Numerical Solution of PDE
(Finite difference method)
We are going to consider
1) Heat equation
2) Steady – State equation
3) Wave equation
١٠٥

Consider the heat equation in the form
( ) ( )
( ) ( )
( ) ( )
x
f
t
x
u
t
t
b
u
t
t
a
u
t
b
x
a
x
u
D
t
u
=
=
=
>
<
<
∂
∂
=
∂
∂
,
,
,
0
,
2
2
ψ
φ
To find u(x,t) using finite difference method.
1. Explicit method
As before let n
i
x
i
x
x
a
x i ,
,
1
,
0
, 0
0 
=
∆
+
=
=
and
١٠٦

( ) ij
j
i
j
u
t
x
u
j
t
j
t
t
t
=
=
∆
+
=
=
,
,
1
,
0
,
0 0
0
denote

The partial derivatives will be as,
( )
( )
( )
( ) )
difference
(central
)
difference
(forward
2
2
1
2
2
1
2
x
O
x
u
u
u
x
u
t
O
t
u
u
t
u
j
i
ij
ij
i
ij
ij
ij
ij
∆
+
∆
+
−
=








∂
∂
∆
+
∆
−
=






∂
∂
−
+
+
Finally, let
( )2
.
x
D
t
r
∆
∆
=
Upon substitution in the equation,
( ) ( )
( )
2
1
1
1 2 x
t
O
u
u
u
r
u
u j
i
ij
j
i
ij
ij ∆
+
∆
+
+
−
=
− −
+
+
١٠٧

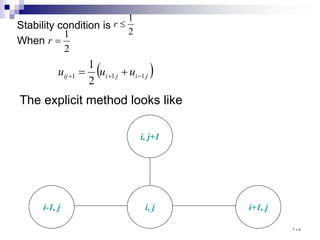
Stability condition is
When
2
1
≤
r
2
1
=
r
( )
j
i
j
i
ij u
u
u 1
1
1
2
1
−
+
+ +
=
The explicit method looks like
i, j
i-1, j i+1, j
i, j+1
١٠٨

In the whole problem
ij
u
a b
x
t
Problem: show that when the local
truncation error will reduce to
The restriction on r causes higher number of
operations which leads to higher round off error.
Hence we move to implicit procedures.
6
1
=
r
( ) ( )
( )
4
2
x
t
O ∆
+
∆
١٠٩

2.Implicit methods
Let us replace by a linear combination of
the known time step and the unknown (next)
time step as follows,








∂
∂
2
2
x
u
( )
1
0
1
1
2
2
2
2
≤
≤
















∂
∂
−
+








∂
∂
=






∂
∂
+
θ
θ
θ
where
ij
ij
ij x
u
x
u
D
t
u
When θ=1 then we have the Explicit method.
When θ= then we have the Implicit Crank -
Nicolson method
2
1
١١٠

When θ=0 then we have the fully implicit method
(backward difference method)
Implicit Crank – Nicolson method
[ ]
1
1
1
1
1
1
1
1 2
2
2
+
+
+
+
−
+
−
+ +
−
+
+
−
=
− j
i
ij
j
i
j
i
ij
j
i
ij
ij u
u
u
u
u
u
r
u
u
The diagram of this method looks like
i-1j+1 ij+1 i+1j+1
i-1j ij i+1j
Rearrangement of the equation yields ١١١

( )
( )

 ,
1
,
0
,
1
,
,
2
,
1
2
1
2
2
1
2
1
1
1
1
1
1
1
=
−
=
+
−
+
=
=
−
+
+
−
+
−
+
+
+
+
−
j
n
i
u
r
u
r
u
r
b
b
u
r
u
r
u
r
j
i
ij
j
i
ij
ij
j
i
ij
j
i
where
This system of (n-1) equation in (n-1) unknown must
be solved for each time step j . Therefore j can be
omitted at each time step, that is
For each j=0,1,…
( )
1
,
,
2
,
1
2
1
2
1
1
−
=
=
−
+
+
− +
−
n
i
b
u
r
u
r
u
r
i
i
i
i
 ١١٢

Taking into consideration the boundary conditions
then in matrix form,


















+
+
=






































+
−
−
+
−
−
+
−
− n
n
n u
r
b
b
u
r
b
u
u
r
r
r
r
r
r
r
O
O
2
2
1
2
2
1
2
2
1
1
2
0
1
1
1











١١٣

This system can be solved by SOR method,
For each j=0,1,…
( )

 ,
1
,
0
;
1
,
,
2
,
1
2
1
2
1
)
(
1
)
(
)
1
(
1
)
(
)
1
(
=
−
=






+
+
−
+
+
+
= +
+
−
+
k
n
i
u
r
u
r
u
r
b
r
u
u k
i
k
i
k
i
i
k
i
k
i
ω
k is the number of iterations
In this special case is found to be
.
opt
ω
n
r
r
b
π
µ
µ
ω cos
1
,
1
1
2
2 +
=
−
+
=
١١٤

Example
Given
( )
( )
( )
( )



<
<
−
<
<
=
>
=
=
>
=
>
<
<
∂
∂
=
∂
∂
20
10
20
10
0
0
,
0
100
,
20
16
.
0
,
0
0
,
0
0
,
20
0
2
2
x
x
x
x
x
u
t
t
u
D
t
t
u
t
x
x
u
D
t
u
Find at x=4,8,12,16
and at x=2,4,…,18
( )
∞
,
x
u
١١٥

As you know
Take r=1 and then and for
each j
( )2
16
.
0
x
t
r
∆
∆
=
4
=
∆x 100
=
∆t
0
0
4
6
6
4
2
5
.
0
0
0
5
.
0
2
5
.
0
0
0
5
.
0
2
5
.
0
0
0
5
.
0
2
5
0
4
3
2
1
=
=












=
























−
−
−
−
−
−
u
u
u
u
u
u
&
that
note
١١٦

100
27273
.
3
09091
.
5
09091
.
5
27273
.
3
4
3
2
1
=







=
=
=
=
⇒ t
u
u
u
u
at
For the next time step and
0
0 =
u 100
5 =
u
545455
.
52
18182
.
4
18182
.
4
545455
.
2
4
3
2
1
=
=
=
=
b
b
b
b
١١٧

Now at t=200
7373
.
55
8582
.
17
33188
.
7
1057
.
3
50
4
3
2
1
4
3
2
1
4
3
2
1
=
=
=
=
⇒












+
=












u
u
u
u
b
b
b
b
u
u
u
u
A
& so on.
١١٨

Elliptic Problems
Consider the Poisson equation
( ) ( )
( ) ( )
m
j
n
i
jk
c
y
ih
a
x
y
x
g
y
x
u
d
y
c
b
x
a
y
x
f
y
u
x
u
y
x
u
j
i
,
,
1
,
0
,
,
1
,
0
,
,
,
,
, 2
2
2
2
2

 =
=
+
=
=
=
=
<
<
<
<
=
∂
∂
+
∂
∂
=
∇
and
for
and
let
boundaries
the
on
with
on
١١٩

a
x =
0 1
x 2
x 3
x 4
x n
x
b =
c
y =
0
1
y
2
y
d
ym =
    




y
x
١٢٠

Let us use the central differential formula for both
derivatives, then
( ) ( ) ( )
1
,
,
1
;
1
,
,
1
2
2
2
2
2
2
2
1
1
2
1
1
2
2
1
1
2
1
1
−
=
−
=
=
+
−
+
+
+
=
+
−
+
+
−
+
−
+
−
+
−
+
−
m
j
n
i
f
k
h
u
k
h
u
u
h
u
u
k
f
k
u
u
u
h
u
u
u
ij
ij
ij
ij
j
i
j
i
ij
ij
ij
ij
j
i
ij
j
i


or
The diagram looks like
١٢١

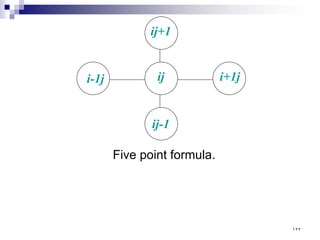
ij+1
i+1j
ij
i-1j
ij-1
Five point formula.
١٢٢

This linear system of (n-1)(m-1) equations and
unknowns can be solved by Gauss – Seidel
method or by SOR method with












+






=
−
+
=
m
n
c
c
b
π
π
ω
cos
cos
2
1
1
1
2
2
where
١٢٣

Example:
Find , given the Poisson equation
( )
j
i y
x
u ,
8
0
,
6
0
2
2
2
2
2
<
<
<
<
−
=
∂
∂
+
∂
∂
y
x
y
u
x
u
u=0 on the boundaries.
Take a) h=k=2
b) h=k=1
For the case a) there are
6 unknowns ij
u
i=1,2 ; j=1,2,3
21
11
22
21
23
31
u
u
u
u
u
u
8
6 x
y
١٢٤

[ ]
3
,
2
,
1
,
2
,
1
8
4
1
1
1
1
1
=
=
+
+
+
+
= +
−
+
−
j
i
u
u
u
u
u ij
ij
j
i
j
i
ij
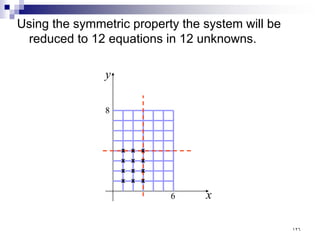
Using the symmetric property (in this particular
problem) we have
56
.
4
56
.
4
72
.
5
72
.
5
56
.
4
56
.
4
23
13
22
12
21
11
=
=
=
=
=
=
u
u
u
u
u
u
For the case b) there are 35 linear equations in
35 unknowns 7
,
,
1
;
5
,
,
1
? 
 =
=
= j
i
uij
١٢٥

Using the symmetric property the system will be
reduced to 12 equations in 12 unknowns.
x x x
x x x
x x x
x x x
8
6 x
y
١٢٦

Preparing the system to be solved by SOR it looks
like
[ ]
=
=
=
−
+
+
+
+
+
= +
+
−
+
+
−
+
b
k
ij
k
ij
k
ij
k
j
i
k
j
i
b
k
ij
k
ij
j
i
u
u
u
u
u
u
u
ω
ω
7
,
,
1
5
,
,
1
4
8
4
)
(
)
(
1
)
1
(
1
)
(
1
)
1
(
1
)
(
)
1
(


The results are as follows












647
.
6
960
.
5
181
.
3
335
.
6
686
.
5
657
.
3
319
.
5
794
.
4
123
.
3
353
.
3
047
.
3
042
.
2
١٢٧

Hyperbolic Problem
(Wave equation)
١٢٨

Two dimensional heat equation in
Cartesian coordinates
(Alternative Direction Implicit method)
ADI
١٢٩

Spline Interpolation
 Linear
 Quadratic
 Cubic Spline
 Quartic
 Quintic
١٣٠

Given a set of data
To construct a cubic spline which fits the data.
To find
.
,
,
,
)
,
( n
1
0
i
y
x i
i 
=
)
(
)
(
)
( i
i
i
2
i
i
3
i
i d
x
x
c
x
x
b
x
x
a
y +
−
+
−
+
−
=
,
,
, i
i
i
i d
c
b
a
for each subinterval [ ]
1
i
i x
x +
+
We should find
for .
,
,
, 1
n
1
0
i −
= 
١٣١

Choosing the second derivatives at the data
Points as auxiliary unknowns.
i
s
writing for
in terms of .
1
n
1
0
i −
= ,
,
, 
i
s
i
i
i
i d
c
b
a ,
,
,
In
.
)
(
)
(
)
( i
i
i
2
i
i
3
i
i d
x
x
c
x
x
b
x
x
a
y +
−
+
−
+
−
=
Let then
i
x
x =
.
i
i d
f = 1
١٣٢

Let then
1
i
x
x +
=
.
i
i
i
2
i
i
3
i
i
1
i f
h
c
h
b
h
a
f +
+
+
=
+
where .
i
1
i
i x
x
h −
= +
Denote
.
)
( i
i
i b
2
x
x
a
6
y
s +
−
=
′
′
=
2
Then at i
x
x =
2
s
b
b
2
s i
i
i
i =
⇒
= 3
١٣٣

.
)
( i
i
1
i
i
i
i
i
1
i h
6
s
s
a
s
h
a
6
s −
=
⇒
+
= +
+
and at 1
i
x
x +
=
4
6
s
h
s
h
2
h
f
f
c 1
i
i
i
i
i
i
1
i
i
+
+ +
−
−
=
Replace and in we get
i
a i
b 2
Now to calculate all ‘s we use the continuity
Of the slope at that is
i
s
i
x
١٣٤

i
x
right
y
left
y )
(
)
( ′
=
′ at
For the interval
[ ] .
)
(
)
(
:
, i
i
i
2
i
i
1
i
i c
x
x
b
2
x
x
a
3
y
x
x +
−
+
−
=
′
+
For the interval
[ ] 1
i
1
i
1
i
2
1
i
1
i
i
1
i c
x
x
b
2
x
x
a
3
y
x
x −
−
−
−
−
− +
−
+
−
=
′ )
(
)
(
:
,
Let in both left and right slopes yields:
i
x
x =
.
١٣٥

Upon substitution of ‘s and rearrangements,
we‘ll have
i
s
i
1
i
1
i
1
i
2
1
i
1
i c
c
h
b
2
h
a
3 =
+
+ −
−
−
−
−
Here
and the unknowns are
)
(
,
, equations
1
n
1
n
1
i −
−
= 
).
(
,
,
, unknowns
1
n
s
s
s n
1
0 +








 −
−
−
=
+
+
+
−
−
+
+
−
−
−
1
i
1
i
i
i
i
1
i
1
i
i
i
i
1
i
1
i
1
i
h
f
f
h
f
f
6
s
h
s
h
2
h
2
s
h )
(
١٣٦

For the extra two unknowns we consider the end
Point conditions.
1.Take and
This condition is called Natural Spline or Free Spline
0
s0 = 0
sn =






−
−
=
+ A
h
f
f
6
s
h
s
h
2
0
0
1
1
0
0
0
2. If and are given then
A
x
f 0 =
′ )
( B
x
f n =
′ )
(
١٣٧

and





 −
−
=
+
−
−
−
−
−
1
n
1
n
n
n
1
n
1
n
1
n
h
f
f
B
6
s
h
2
s
h
Are two extra equations.
This condition is called Clamped spline.
3. Take and
1
0 s
s = .
1
n
n s
s −
=
١٣٨

Advanced Engineering Mathematics

More Related Content

What's hot

Similar to Advanced Engineering Mathematics

Recently uploaded

Advanced Engineering Mathematics