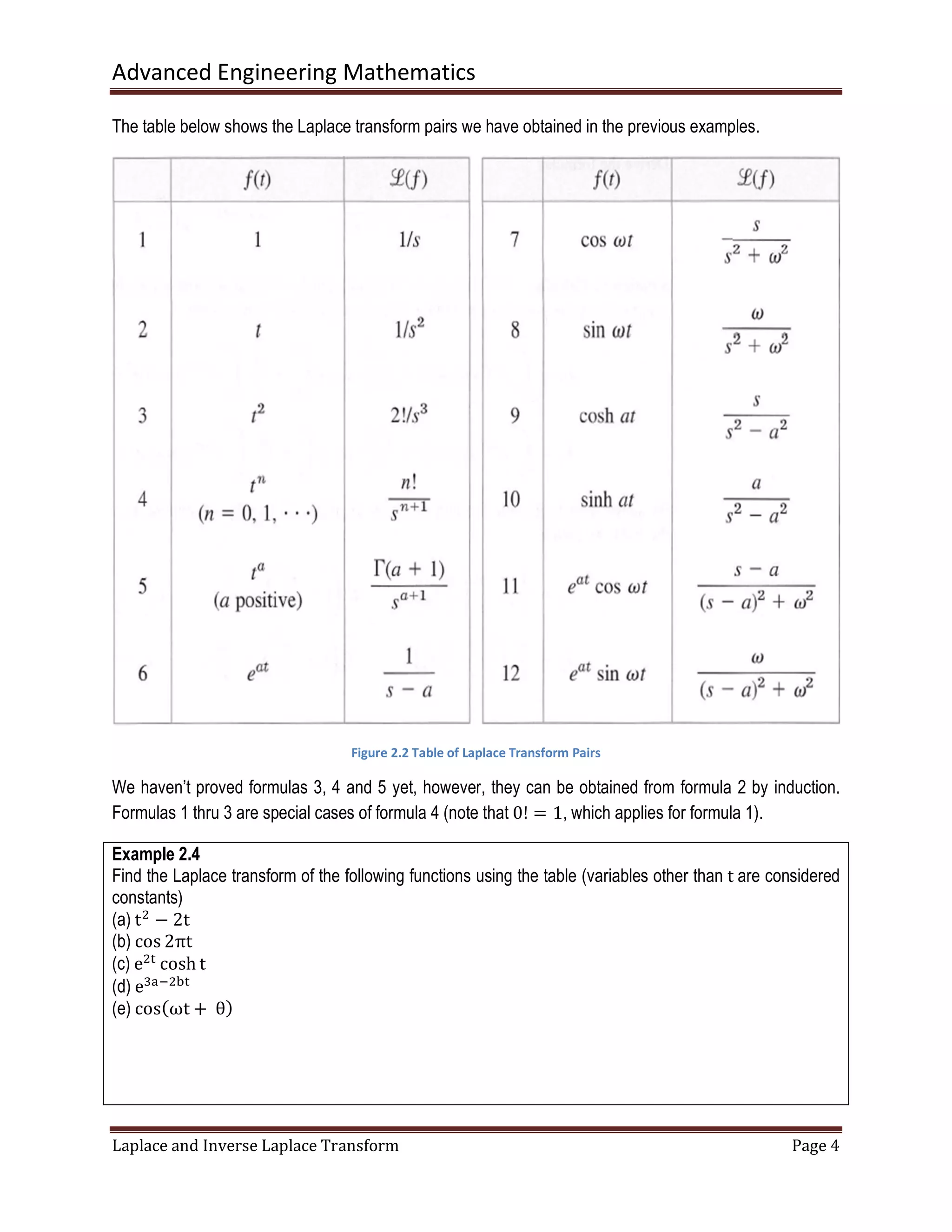
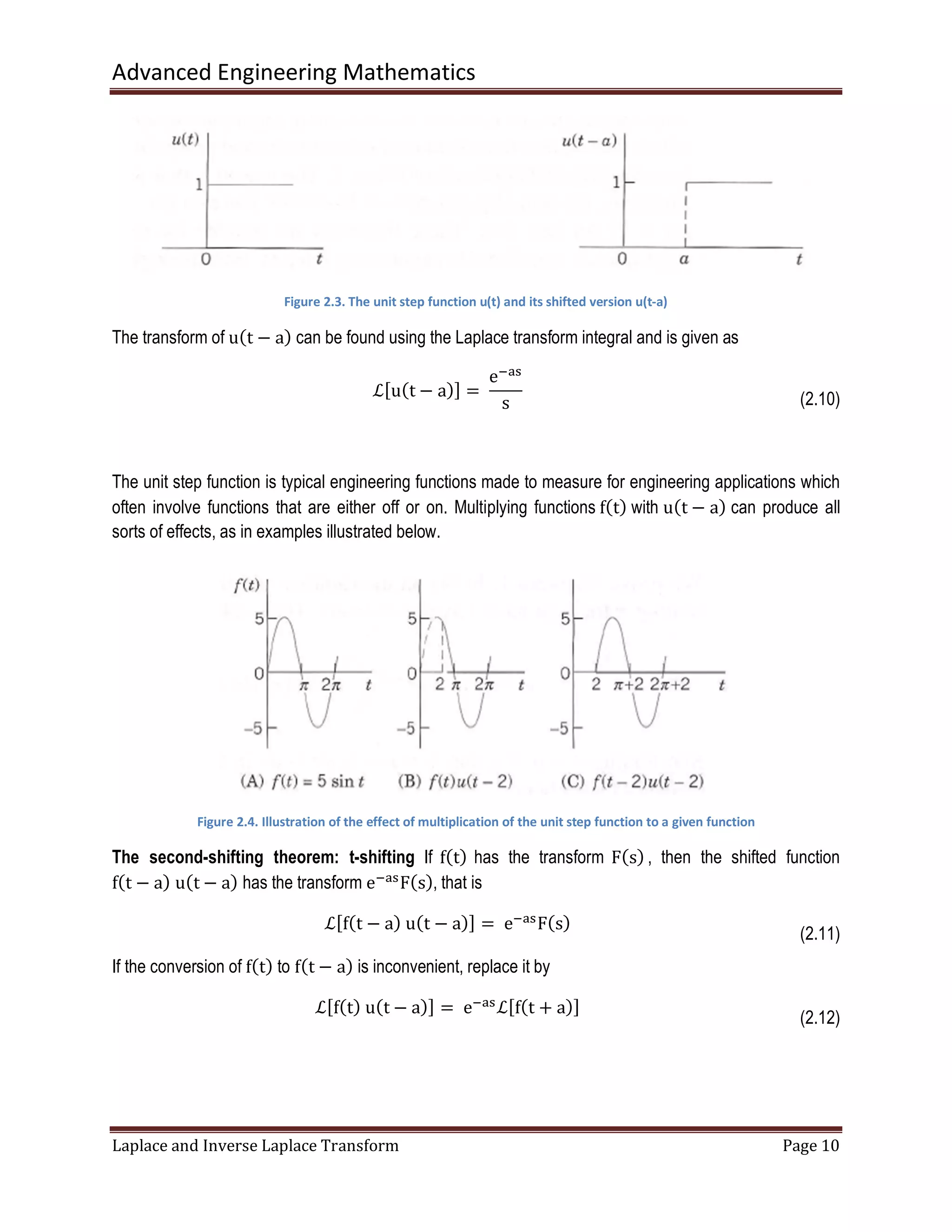
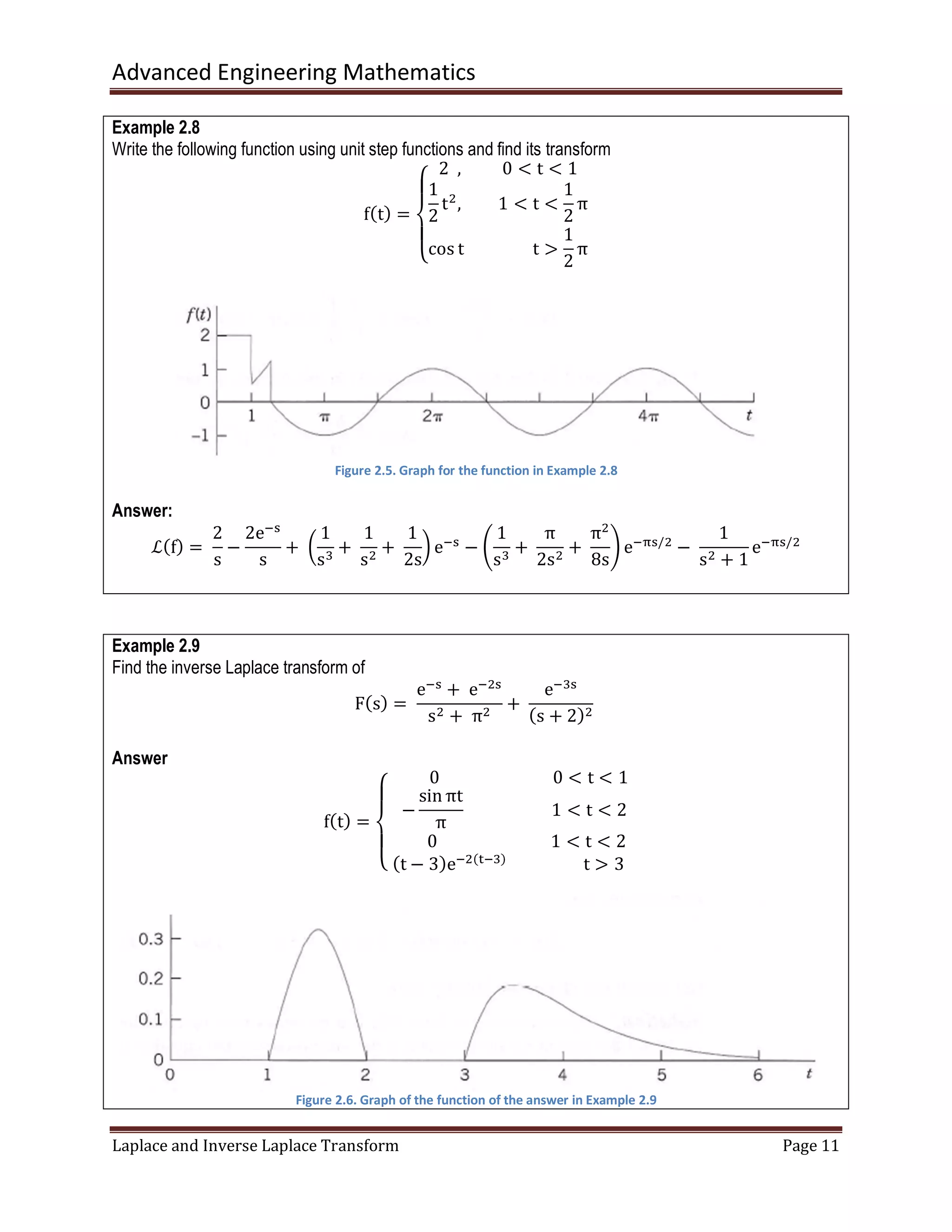
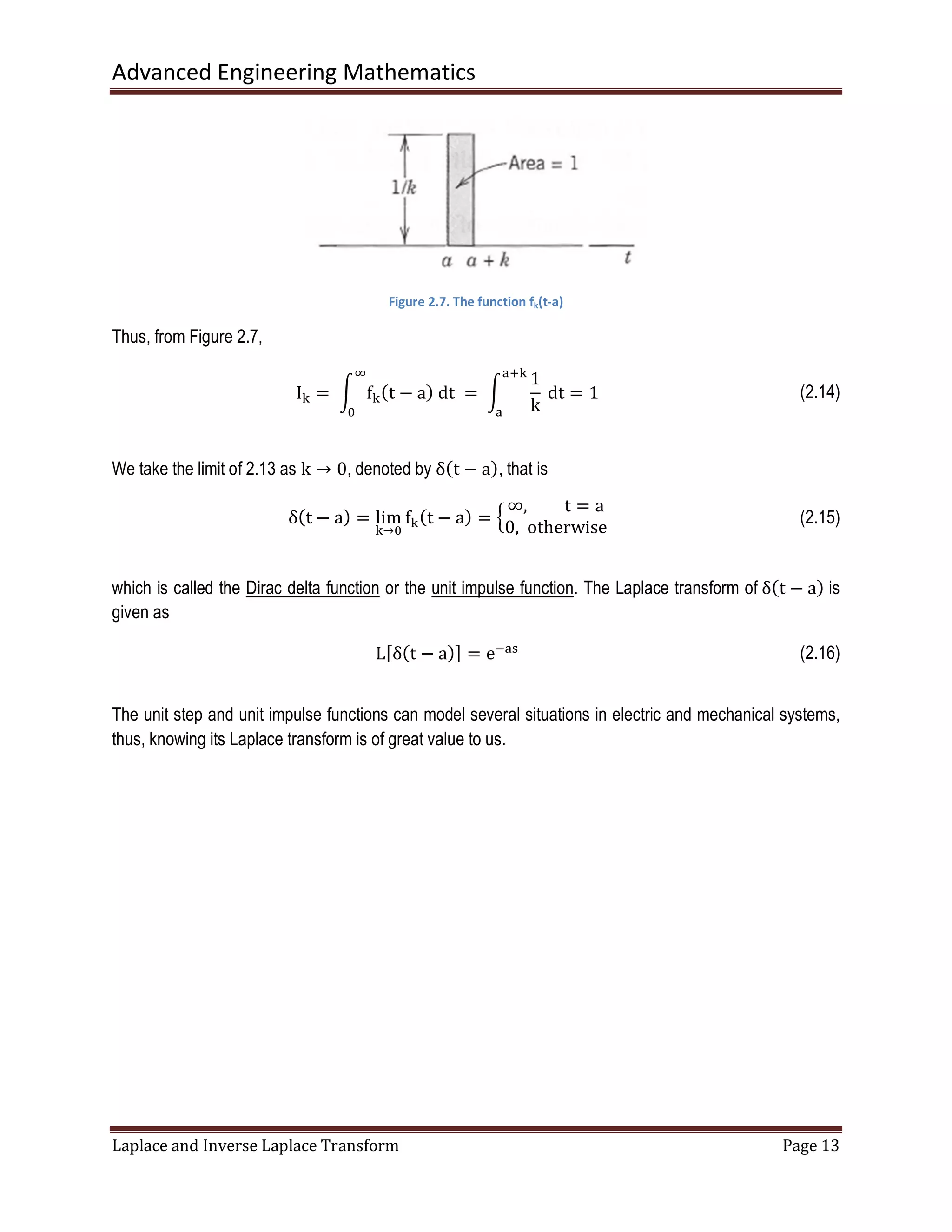
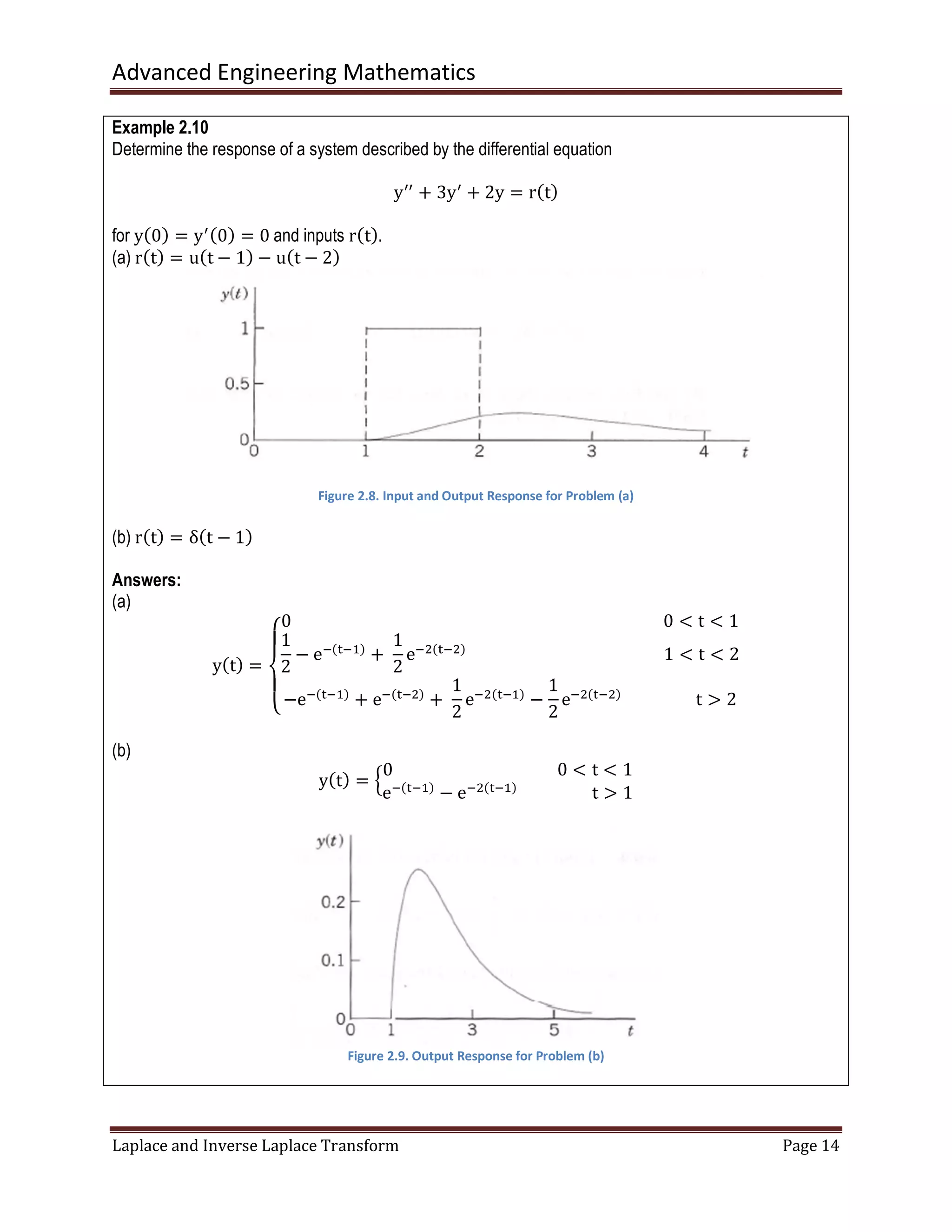
The document discusses the Laplace transform and its applications. The Laplace transform maps functions defined in the time domain to functions defined in the complex frequency domain. It makes solving differential equations easier by converting calculus operations into algebra. Some key properties include: the Laplace transform of derivatives can be obtained algebraically instead of using calculus rules, and the transform allows shifting between time and complex frequency domains. Examples are provided to illustrate definitions, properties, and how to use Laplace transforms to solve initial value problems for ordinary differential equations.